关于l-路和图的超欧拉性

李晓璞，刘 娟

(新疆师范大学 数学科学学院，乌鲁木齐 830017)

0 引 言

本文只考虑无向图中没有自环和重边的简单图，除非特别说明，其他未给出的术语和定义可以参考文献[1]和[2]。令图G=VG,EG其中图的点集为VG,图的边集为EG。在这篇文章中，我们用符号xy表示图G中连接点x和点y的一条边。符号a,b表示从a到b之间的所有整数。图G中的道是一个交替序列W=v0e1v1e2…vl-1elvl，对于每一个i∈0,l,其中vi为点，ei为边使得ei=vivi+1。如果v0=vl，则称W是一个闭道，否则是开道。当W的边在上下文中已知时，可以记W为v0v1…vl。如果v0≠vl，则v0和vl是W的两个端点，道的长度是道中所含边的条数。图G中的一个迹是一个所有边都不同的道。一个路是一个所有点都不同的道。路的长度是路中所含边的条数，长度为l的路叫做l-路，它包含l+1个点。如果W中v0v1…vl是不同的点，l≥2，并且v0=vl，则称W是一个圈。如果对于图G中每对不同的点x，y都存在连接x和y的路，则称G是连通图。令G1和G2是两个图，如果VG1∩VG2=∅,则称G1和G2是点不交的图。如果EG1∩EG2=∅,则称G1和G2是边不交的图。如果VH⊆VG,EH⊆EG并且EH中的每一条边的两个端点都在VH中，则称H是G的一个子图。如果VH=VG，则称H是G的一个生成子图。对于G中任意一个点v，用G-v表示从图G中删去点v及其所关联的边所得到的G的子图，称为G的点删除子图。对于G中任意一条边e，用G-e表示从图G中删去边e所得到的G的子图，称为G的边删除子图。如果一个图G包含一条闭迹使得EW=EG,则称G是欧拉图。如果一个图G包含一条闭迹使得VW=VG,或包含一个生成欧拉子图，则称G是超欧拉图。

定义1 在图G中，如果对于每一个点v∈VG，满足点删除子图G-v是超欧拉图，那么G称为D-超欧拉图。

定义2 在超欧拉图G中，如果对于每一个点v∈VG，满足点删除子图G-v是超欧拉图，那么G称为T-超欧拉图。

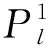
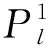
Boesch,Suffel和Tindell[3]在1977年提出了超欧拉问题，他们致力于刻画出包含生成欧拉子图的无向图，与此同时，他们表示这个问题是极其困难的。Pulleyblank[4]在1979年证明了判定一个无向图(甚至包含平面无向图)是否是超欧拉的是NP-完全的。Catlin[5]在1988年提出了超欧拉图的约化方法，是研究此类问题的重要工具。关于超欧拉问题的研究方法，研究进展及其应用，参见文献[6-9]。

在文献[10]中，我们知道两个超欧拉有向图的2-和不一定是超欧拉有向图。在文献[11]中，介绍了有向图中l-路和的概念，并且给出了一些两个有向图的l-路和是超欧拉图的充分条件。由这些结论，自然而然地想到了在无向图中有关超欧拉图的2-和与l-路和问题。在本文中，我们将介绍两个无向图的2-和与l-路和是超欧拉图、D-超欧拉图和T-超欧拉图的一些充分条件。

1 主要结论

首先，我们讨论两个无向图的l-路和是超欧拉图、D-超欧拉图和T-超欧拉图的一些充分条件。

定理1 设G1和G2是两个点不交的超欧拉图。在G1⊕l+1G2中，如果Gi有一个生成欧拉子图Sii=1,2，使得ES1∩ES2=∅。那么G1⊕l+1G2是超欧拉图。

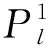
定理2 设G1和G2是两个点不交的D-超欧拉图。对于任意的点vi∈VGi，在G1⊕l+1G2中，如果Gi-vi有一个生成欧拉子图SGi-vii=1,2，使得ESG1-v1∩ESG2-v2=∅。那么G1⊕l+1G2是D-超欧拉图。

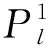
情形1v=vj，∀j∈0,l

如果v=vj，由D-超欧拉图的定义，可知G1-vj是超欧拉图，所以G1-vj有一个生成欧拉子图，记作SG1-vj；同样的，G2-vj是超欧拉图，所以G2-vj有一个生成欧拉子图，记作SG2-vj，并且ESG1-vj∩ESG2-vj=∅，那么SG1-vj∪SG2-vj是G1⊕l+1G2-vj的一个生成欧拉子图。即G1⊕l+1G2是D-超欧拉图。

情形2v∈VG1⊕l+1G2vj,∀j∈0,l

如果v∈VG1vj，由D-超欧拉图的定义，可知G1-v是超欧拉图，所以G1-v有一个生成欧拉子图，记作SG1-v；同样的，G2-v0是超欧拉图，所以G2-v0有一个生成欧拉子图，记作SG2-v0，并且ESG1-v∩ESG2-v0=∅，那么SG1-v∪SG2-v0是G1⊕l+1G2-v的一个生成欧拉子图。如果v∈VG2vj,由D-超欧拉图的定义，可知G2-v是超欧拉图，所以G2-v有一个生成欧拉子图，记作SG2-v；同样的，G1-v0是超欧拉图，所以G1-v0有一个生成欧拉子图，记作SG1-v0，并且ESG2-v∩ESG1-v0=∅，那么SG2-v∪SG1-v0是G1⊕l+1G2-v的一个生成欧拉子图。即G1⊕l+1G2是D-超欧拉图。

定理3 设G1和G2是两个点不交的图。G1是一个T-超欧拉图，G2是一个D-超欧拉图。在G1⊕l+1G2中，如果G1有一个生成欧拉子图SG1，对于任意点v2∈VG2，G2-v2有一个生成欧拉子图SG2-v2，使得ESG1∩ESG2-v2=∅。那么G1⊕l+1G2是T-超欧拉图。

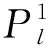
由T-超欧拉的定义，可知G1是超欧拉图，所以G1有一个生成欧拉子图，记作SG1。由D-超欧拉的定义，可知G2-v0是超欧拉图，所以G2-v0有一个生成欧拉子图，记作SG2-v0。并且ESG1∩ESG2-v0=∅，所以SG1∪SG2-v0是G1⊕l+1G2的一个生成欧拉子图，即G1⊕l+1G2是超欧拉图。

对于任意点v∈VG1⊕l+1G2，需证明任意点删除子图G1⊕l+1G2-v是超欧拉图，我们分以下两种情形讨论：

情形1v=vj，∀j∈0,l

如果v=vj，由T-超欧拉图的定义，可知G1-vj是超欧拉图，所以G1-vj有一个生成欧拉子图，记作SG1-vj；由D-超欧拉图的定义，可知G2-vj是超欧拉图，所以G2-vj有一个生成欧拉子图，记作SG2-vj，并且ESG1-vj∩ESG2-vj=∅，那么SG1-vj∪SG2-vj是G1⊕l+1G2-vj的一个生成欧拉子图。即G1⊕l+1G2是T-超欧拉图。

情形2v∈VG1⊕l+1G2vj，∀j∈0,l

如果v∈VG1vj，由T-超欧拉图的定义，可知G1-v是超欧拉图，所以G1-v有一个生成欧拉子图，记作SG1-v；由D-超欧拉图的定义，可知G2-v0是超欧拉图，所以G2-v0有一个生成欧拉子图，记作SG2-v0，并且ESG1-v∩ESG2-v0=∅，那么SG1-v∪SG2-v0是G1⊕l+1G2-v的一个生成欧拉子图。如果v∈VG2vj，由D-超欧拉图的定义，可知G2-v是超欧拉图，所以G2-v有一个生成欧拉子图，记作SG2-v；由T-超欧拉图的定义，可知G1是超欧拉图，所以G1有一个生成欧拉子图，记作SG1，并且ESG1∩ESG2-v=∅，那么SG1∪SG2-v是G1⊕l+1G2-v的一个生成欧拉子图。即G1⊕l+1G2是T-超欧拉图。

以上我们讨论了两个无向图的l-路和是超欧拉图、D-超欧拉图和T-超欧拉图的一些充分条件。

特别的，以下我们将讨论两个无向图的2-和是超欧拉图、D-超欧拉图和T-超欧拉图的一些更优的充分条件。

定理4 设G1和G2是两个点不交的超欧拉图，那么G1⊕2G2是超欧拉图。

证明因为G1和G2是超欧拉图，即Gi有一个生成欧拉子图Sii=1,2。由G1⊕2G2的定义可知，如果ES1∩ES2≠∅,令ES1∩ES2=e，那么S1∪S2-e是G1⊕2G2的一个生成欧拉子图；如果ES1∩ES2=∅，那么S1∪S2是G1⊕2G2的一个生成欧拉子图，即G1⊕2G2是超欧拉图。

定理5 设G1和G2是两个点不交的D-超欧拉图，那么G1⊕2G2是D-超欧拉图。

证明设e1=v11v12∈EG1和e2=v21v22∈EG2是两条不相交的边。由G1⊕2G2的定义，令v11=v21=v1，v12=v22=v2。对于任意点v∈VG1⊕2G2，需证明任意点删除子图G1⊕2G2-v是超欧拉图，我们分以下两种情形讨论：

情形1v=v1或v=v2

如果v=v1，由D-超欧拉图的定义，可知G1-v1是超欧拉图，所以G1-v1有一个生成欧拉子图，记作SG1-v1；同样的，G2-v1是超欧拉图，所以G2-v1有一个生成欧拉子图，记作SG2-v1，那么SG1-v1∪SG2-v1是G1⊕2G2-v1的一个生成欧拉子图。如果v=v2，由D-超欧拉图的定义，可知G1-v2是超欧拉图，所以G1-v2有一个生成欧拉子图，记作SG1-v2；同样的，G2-v2是超欧拉图，所以G2-v2有一个生成欧拉子图，记作SG2-v2，那么SG1-v2∪SG2-v2是G1⊕2G2-v2的一个生成欧拉子图。即G1⊕2G2是D-超欧拉图。

情形2v∈VG1⊕2G2v1,v2

如果v∈VG1v1,v2，由D-超欧拉图的定义，可知G1-v是超欧拉图，所以G1-v有一个生成欧拉子图，记作SG1-v；同样的，G2-v1是超欧拉图，所以G2-v1有一个生成欧拉子图，记作SG2-v1，那么SG1-v∪SG2-v1是G1⊕2G2-v的一个生成欧拉子图。如果v∈VG2v1,v2，由D-超欧拉图的定义，可知G2-v是超欧拉图，所以G2-v有一个生成欧拉子图，记作SG2-v；同样的，G1-v1是超欧拉图，所以G1-v1有一个生成欧拉子图，记作SG1-v1，那么SG2-v∪SG1-v1是G1⊕2G2-v的一个生成欧拉子图。即G1⊕2G2是D-超欧拉图。

定理6 设G1和G2是两个点不交的图。G1是一个T-超欧拉图，G2是一个D-超欧拉图。那么G1⊕2G2是T-超欧拉图。

证明设e1=v11v12∈EG1和e2=v21v22∈EG2是两条不相交的边。由G1⊕2G2的定义，令v11=v21=v1，v12=v22=v2。

由T-超欧拉的定义，可知G1是超欧拉图，所以G1有一个生成欧拉子图，记作SG1。由D-超欧拉的定义，可知G2-v1是超欧拉图，所以G2-v1有一个生成欧拉子图，记作SG2-v1，所以SG1∪SG2-v1是G1⊕2G2的一个生成欧拉子图，即G1⊕2G2是超欧拉图。

对于任意点v∈VG1⊕2G2，需证明任意点删除子图G1⊕2G2-v是超欧拉图，我们分以下两种情形讨论：

情形1v=v1或v=v2

如果v=v1，由T-超欧拉图的定义，可知G1-v1是超欧拉图，所以G1-v1有一个生成欧拉子图，记作SG1-v1；由D-超欧拉图的定义，可知G2-v1是超欧拉图，所以G2-v1有一个生成欧拉子图，记作SG2-v1，那么SG1-v1∪SG2-v1是G1⊕2G2-v1的一个生成欧拉子图。如果v=v2，由T-超欧拉图的定义，可知G1-v2是超欧拉图，所以G1-v2有一个生成欧拉子图，记作SG1-v2；由D-超欧拉图的定义，可知G2-v2是超欧拉图，所以G2-v2有一个生成欧拉子图，记作SG2-v2，那么SG1-v2∪SG2-v2是G1⊕2G2-v2的一个生成欧拉子图。即G1⊕2G2是T-超欧拉图。

情形2v∈VG1⊕2G2v1,v2

如果v∈VG1v1,v2，由T-超欧拉图的定义，可知G1-v是超欧拉图，所以G1-v有一个生成欧拉子图，记作SG1-v；由D-超欧拉图的定义，可知G2-v1是超欧拉图，所以G2-v1有一个生成欧拉子图，记作SG2-v1，那么SG1-v∪SG2-v1是G1⊕2G2-v的一个生成欧拉子图。如果v∈VG2v1,v2，由D-超欧拉图的定义，可知G2-v是超欧拉图，所以G2-v有一个生成欧拉子图，记作SG2-v；由T-超欧拉图的定义，可知G1是超欧拉图，所以G1有一个生成欧拉子图，记作SG1，那么SG2-v∪SG1是G1⊕2G2-v的一个生成欧拉子图。即G1⊕2G2是T-超欧拉图。

2 总 结

超欧拉问题的研究是一个比较新的研究领域，具有很广阔的研究前景。本文类比出了无向图中l-路和及2-和的概念，并且给出了在无向图中D-超欧拉图和T-超欧拉图的定义，通过进行运算及讨论探究得到了一系列关于超欧拉的充分条件。本文是从无向图的角度，探究关于超欧拉图的l-路和及2-和运算之后的结论。我们还可以从有向图的角度可虑这个问题，看看在有向图的条件下，是否可以探究出关于超欧拉有向图的一些结论。也可以考虑在无向、有向的条件下，对于D-超欧拉图和T-超欧拉图进行其它的运算，能否得到一些结论，这些都是值得我们继续讨论和探究的问题。