例析新高考数学必修2《立体几何中的角》

广东省佛山市华附南海实验高中(528200)

周建军 ●



例析新高考数学必修2《立体几何中的角》

广东省佛山市华附南海实验高中(528200)

周建军 ●

在新课标高考中，广东省将采用全国卷，而全国卷中试题大多以中档题为主，立体几何题已经不再如广东卷那样属于送分题.在全国卷的立体几何问题中，通常第一问是证明直线的位置关系，第二问是求角.有关立体几何中角的问题的求解已经成为阻碍学生得分的主要因素.本文将以典型例题来阐述必修2立体几何中角的有关问题的有效教学和处理模式.

线线角；线面角；二面角；等体积法；空间角；空间想象能力

一、异面直线所成的角(线线角)

例1 如图1，已知正方体ABCD-A1B1C1D1中，E为C1D1的中点，则异面直线AE与BC所成角的余弦值为____.

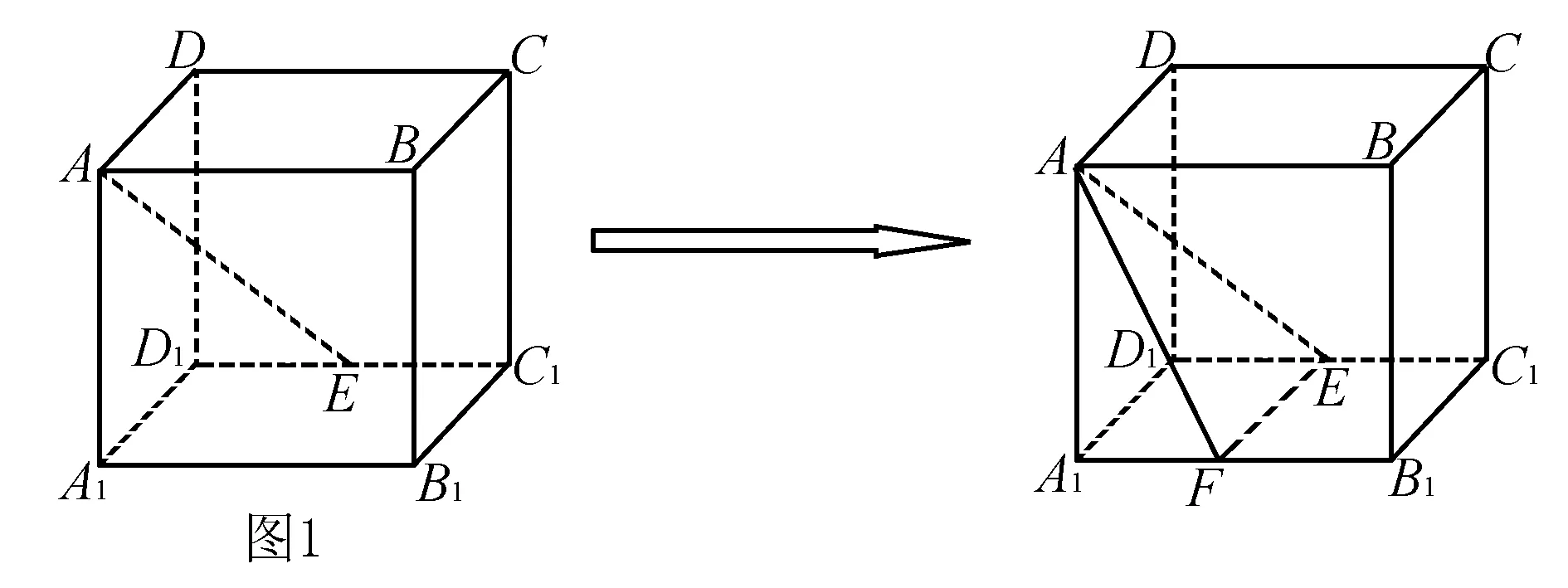
思考 异面直线所成的角本是空间角，不便直接求解，可考虑将其中一条直线平移至与另一条直线相交，构建三角形，转化为平面角，以三角形为载体，通过解三角形进行求解.

解析 过点E作EF∥B1C1交A1B1于F，连结AF. 在正方体ABCD-A1B1C1D1中，BC∥B1C1. 又EF∥B1C1，所以BC∥EF. 直线AE与EF所成的角即为异面直线AE

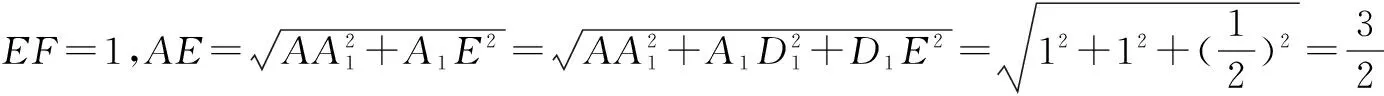
在正方体ABCD-A1B1C1D1中，B1C1⊥平面ABB1A1.

∵EF∥B1C1，∴EF⊥平面ABB1A.

又AF⊂平面ABB1A1，∴EF⊥AF.

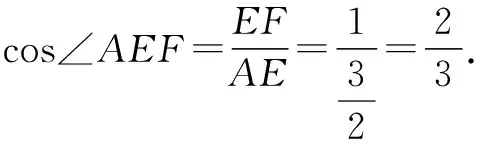
二、直线与平面所成的角(线面角)

例2 如图2，在正方体ABCD-A1B1C1D1中，直线A1B和平面A1B1CD所成角的大小为____.

思考1 根据线面角的定义，线面角指的是斜线和斜线在平面内的射影的夹角.在这里，要得到斜线A1B的射影，需过点B作出平面A1B1CD的垂线. 如何作出垂线并证明之是解决问题的关键.

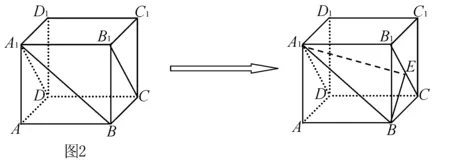
解析 过点B作BE⊥B1C于E，连结A1E.

在正方体ABCD-A1B1C1D1中，DC⊥平面BCC1B1.

∵BE⊂平面BCC1B1，∴DC⊥BE.

又BE⊥B1C，DC∩B1C=C，∴BE⊥平面A1B1CD.

∴直线A1B在平面A1B1CD内的射影是A1E.

∴A1B和A1E所成的角，即∠BA1E为直线A1B和平面A1B1CD所成的角.

∵BE⊥平面A1B1CD，A1E⊂平面A1B1CD，

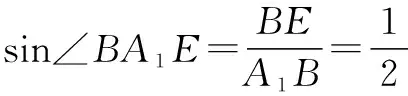
又∠BA1E为锐角，∴∠BA1E=30°.

因此，直线A1B和平面A1B1CD所成的角为30°.

小结 在这里，有一种“作一得二”的思想可以归纳.过点B作BE⊥B1C于E，表面上只有一个垂直BE⊥B1C，但实际上BE处在被DC垂直的平面BCC1B1内，所以又可得到另一个垂直DC⊥BE. 作一个垂直，而得到两个垂直，这种思想用来作面的垂线在立体几何中很常见.当然，也可先证明平面A1B1CD⊥平面BCC1B1，再找交线B1C，过点B作BE⊥B1C于E，从而得到BE⊥平面A1B1CD.

思考2 当过点作面的垂线不便于作出来时，那么斜线在面内的射影就不便找到，但它却是真实存在的.此时，可考虑用等体积法来求出点到面的距离，从而求解线面角.这种方法对图形本身的要求不高，也不需过多地作辅助线，但要求进行计算.

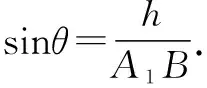
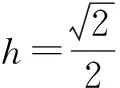
又θ是锐角，∴θ=30°.

因此，直线A1B和平面A1B1CD所成的角为30°.

三、平面与平面所成的角(二面角)

例3 如图3，在正四棱锥P-ABCD中，PO⊥平面ABCD，∠APC=60°，则

(1)二面角P-AD-C的余弦值为____.

(2)二面角A-PB-C的余弦值为____.

(1)思考 二面角是空间角，不可直接求解.求解二面角，通常先作出二面角的平面角.在这里，可考虑用三垂线定理(或逆定理)的思想来作出二面角的平面角.

注 (Ⅰ)三垂线定理：平面内的一条直线，如果它和这个平面的一条斜线在平面内的射影垂直，那么它也和这条斜线垂直.

(Ⅱ)三垂线定理的逆定理：平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直.

解析 过点O作OH⊥AD于H，连结PH.

∵PO⊥平面ABCD，AD⊂平面ABCD，∴PO⊥AD.

又OH⊥AD，PO∩OH=O，

∴AD⊥平面POH.

又PH⊂平面POH，∴AD⊥PH.

又OH⊥AD，∴∠PHO是二面角P-AD-C的平面角.

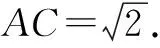
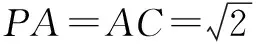
∵OH⊥AD，CD⊥AD，∴OH∥CD.

在正四棱锥P-ABCD中，PO⊥平面ABCD，

∴O为正方形ABCD的中心，即为AC的中点.

∴AH=HD.

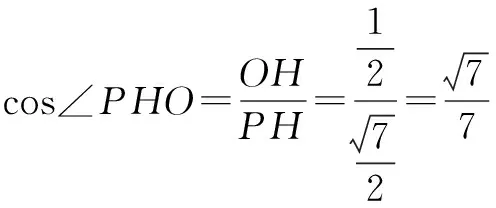
(2)思考 在正四棱锥P-ABCD中，△APB≅△CPB. 两个三角形有明显的对称性.此时，可作出一个三角形的高，顺应得出另一个三角形的高，两条高所形成的角即为二面角的平面角.

妈妈和劳拉、玛丽在篷车里吃着面包和糖蜜，马吃着挂在脖颈上的饲料袋里的谷粒，爸爸则走进那家商店用兽皮交换旅途上需要的东西。他们不能在镇子里待得太久，因为他们必须在当天穿过丕平湖。

解析 过点A作AE⊥PB于E，连结CE.∵△APB≅△CPB，∴CE⊥PB.

又AE⊥PB，∴∠AEC是二面角A-PB-C的平面角.

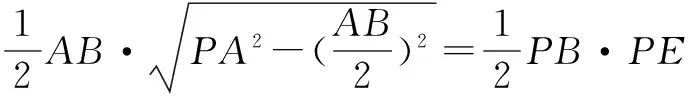
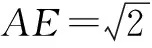
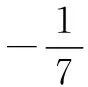
应用

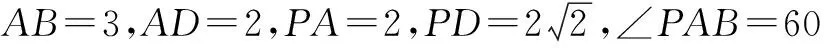
(1)求异面直线PC与AD所成角的正切值；

(3)求直线PD与平面PBC所成角的正弦值.

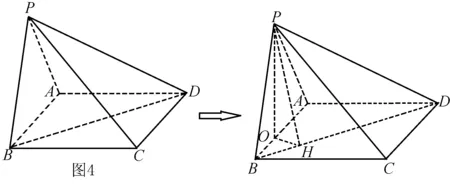
(1)思考 异面直线PC与AD形成的是空间角，依题意，可考虑将AD平移至BC，转化为PC与BC之间的夹角，将其放在△PBC中进行求解.

解析 ∵四边形ABCD为矩形，∴AD∥BC.

∴PC与BC所成的角即为异面直线PC与AD所成角，即为∠PCB.

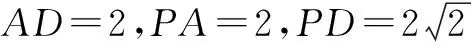
∴AD2+PA2=PD2.∴AD⊥PA.

又四边形ABCD是矩形，∴AD⊥AB.又PA∩AB=A，

∴AD⊥平面PAB.

又AD∥BC，∴BC⊥平面PAB. 又PB⊂平面PAB，

∴BC⊥PB.

在△PAB中，AB=3，PA=2，∠PAB=60°，

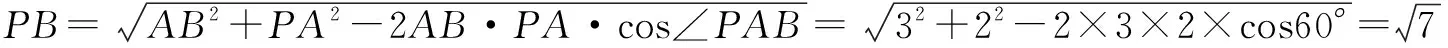
在矩形ABCD中，BC=AD=2.

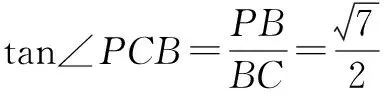
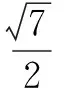
(2)思考 由(1)知，AD⊥平面PAB. 可仿照例2中思考1的解析方法，“作一得二”作出平面ABD的垂线，从而构建三垂线定理(或逆定理)的思想来作出二面角的平面角.

解析 过点作PO⊥AB于O，过点O作OH⊥BD于H，连结PH.

由(1)知，AD⊥平面PAB. 又PO⊂平面PAB，∴AD⊥PO. 又PO⊥AB，AD∩AB=A,∴PO⊥平面ABD.∵BD⊂平面ABD，∴PO⊥BD.

又OH⊥BD,PO∩OH=O,∴BD⊥平面POH.

又PH⊂平面POH，∴BD⊥PH.又OH⊥BD，∴∠PHO是二面角P-BD-A的平面角.

∵PO⊥平面ABD，OH⊂平面ABD，∴PO⊥OH.

∴OB=AB-OA=3-1=2.

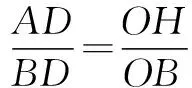
(3)思考 这里的线面角不容易作出斜线在面上的射影，很难作图产生线面角，故优先考虑用等体积法进行求解.

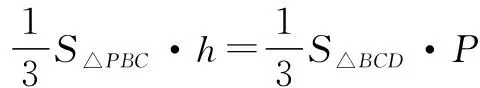
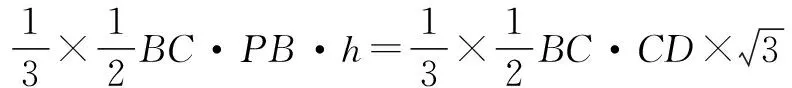
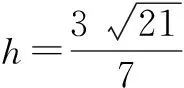
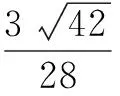
[1] 中华人民共和国教育部. 普通高中数学课程标准(实验)[M]. 北京：人民教育出版社，2003.

[2] 中华人民共和国教育部. 全日制普通高级中学数学教学大纲[M]. 北京：人民教育出版社，2002.

[3] 人民教育出版社课程教材研究所，中学数学课程教材研究开发中心. 普通高中课程标准实验教科书：数学2 [M]. 3版. 北京：人民教育出版社，2007.

G632

B

1008-0333(2016)22-0012-03