有限差分卡尔曼滤波算法估计污染物在地下水中迁移转化——在辽河流域的应用

王新民，陈慧颖，马旭东

(长春工业大学 基础科学学院，吉林 长春 130012)



有限差分卡尔曼滤波算法估计污染物在地下水中迁移转化
——在辽河流域的应用

王新民，陈慧颖*，马旭东

(长春工业大学 基础科学学院，吉林 长春 130012)

采用有限差分方法,用差商代替微商导出卡尔曼滤波的转移矩阵，从而估计其主要污染物氨氮的迁移转化，为辽河流域治理提供技术支持。

地下水污染；污染物迁移转化；有限差分；卡尔曼滤波

0 引 言

在过去的几十年里，地表水和地下水污染问题已成为地质科学研究的主要领域,因为它对人类社会经济生活有着重要影响。包括污染物的跟踪、地下水水质的预测。目前已经建立了很多针对不同情况的地下水污染数值模型，在大多数情况下，这些模型许多都是带有参数的偏微分方程，模型是否可靠很多情况下取决于水文地质参数以及边界条件的概化是否准确。为此，许多学者们提出了大量关于水文地质参数估计的方法，用以提高模型的预测能力，如蒙特卡罗法、正则化方法等。这些方法在某种程度上可以处理模型参数的不确定性，但忽略了构建模型时模型本身存在的误差以及获得数据时的测量误差。参数估计的另一种选择是连续的数据同化，卡尔曼滤波器(KF)是最佳的顺序同化方案之一，它可以用来滤除观测数据中的噪声和干扰，以达到最佳的状态估计[1-2]。当模型和测量噪声在非线性模型情况下，可使用扩展卡尔曼滤波器[3](EKF)将模型线性化。并且可将状态变量(即水体中待求的污染物浓度)和相关参数合并为一个向量进行计算，这样可将模型参数和污染物浓度同时确定。但由于实际应用中扩展卡尔曼滤波线性化过程的不稳定且Jacobian矩阵的推导十分复杂，文中采用有限差分的方法代替扩展卡尔曼滤波中的Taylor展开，导出卡尔曼滤波的转移矩阵。

1 水污染模型的差分格式

有限差分法[4]的基本思想是用差商近似代替方程中的微商，将连续的问题离散化，然后耦合初始条件及边界条件，求解封闭的线性代数方程组。这里只需完成第一部分。

考虑如下地下水污染模型:

式中：C——污染物浓度;

Dx，Dy——弥散系数;

u——流速。

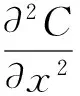
2 卡尔曼滤波技术在地下水污染模型中的应用

卡尔曼滤波有两个基本方程[5]：状态方程和测量方程。对于地下水污染系统而言，状态方程是描述地下水污染物运移过程的方程式，传统的卡尔曼滤波是针对线性系统的一种算法，而实际的观测模型往往是非线性的，包括地下水污染模型。文中通过上述有限差分法将模型线性化，加上误差随机项，即可得到卡尔曼滤波的系统状态方程：

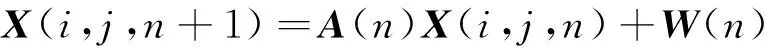
系统的测量方程为：

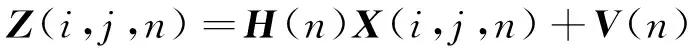
式中：Z(i,j,n)——n时刻节点观测的矢量值；

H(n)——测量矩阵，由监测孔相对于模型分节点的位置确定；

W(n)，V(n)——误差项，一般假设相互独立，服从高斯分布，并具有下列协方差矩阵

卡尔曼滤波算法主要包括两步[6]：预测和更新。在预测阶段，用运移模型根据t-1时刻状态向量和误差协方差矩阵预测t时刻的状态和协方差矩阵。

式中：“∧”——估计值；

“—”——前面式子算出来的估计值。

更新阶段是对模型状态和参数进行时间更新。更新过程可以表示为：

为卡尔曼增益，类似一个信心指数，用来说明对测量值还是预测值的信心程度,I是单位矩阵。经过足够多步的计算，模型状态、参数的估计值就会逐渐逼近真实值，从而达到状态参数估计的目的[7]。

3 实例分析

研究区位于沈阳市区西南部，浑河北岸漫滩地区，地理坐标为北纬41°30′～42°00′，东经123°00′～123°40′，面积约37.88 km2。研究区内地表水体主要有浑河及其支流细河，属于辽河水系。地下水水质以“三氮”(氨氮、硝酸根离子、亚硝酸根离子)污染为主。其中氨氮主要来源于人和动物的排泄物、降水的垂直入渗、工业废水以及河流的侧向补给。主要排泄方式为人工开采。研究区地下径流方向为由东北向西南，东南部受浑河影响，西北部临界细河，可概化为一类定浓度边界；北部和西部是地下水侧向径流补给和排泄段，可概化为二类定通量边界[8-9]。依据上述特征建立数学模型：

式中：R——阻滞系数;

c——溶质氨氮的浓度;

D——弥散系数;

V——流速;

λ——衰变常数，氨氮在运移过程中会不断衰变，发生硝化反应;

Ω——整个模型区域;

Γ1——定浓度边界;

Γ2——通量边界;

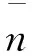
ck(x,y,t)——已知的初始浓度分布;

g(x,y,t)——已知函数，表示对流弥散通量。

研究区采用100×100等间距有限差分法离散，共剖分矩形单元格17 402个。研究区网格剖分图如图1所示。

图1 研究区网格剖分图

运用前述的卡尔曼滤波最优估计算法，选取已知监测井45个，统一测定时间为2011年3月至2012年9月，测量误差的方差取0.002 5。

校正后的弥散系数和噪声标准差见表1。

表1 校正前后的模型参数表

研究区2011年3月实测初始氨根浓度等值线图和估计协方差等值线图分别如图2和图3所示。

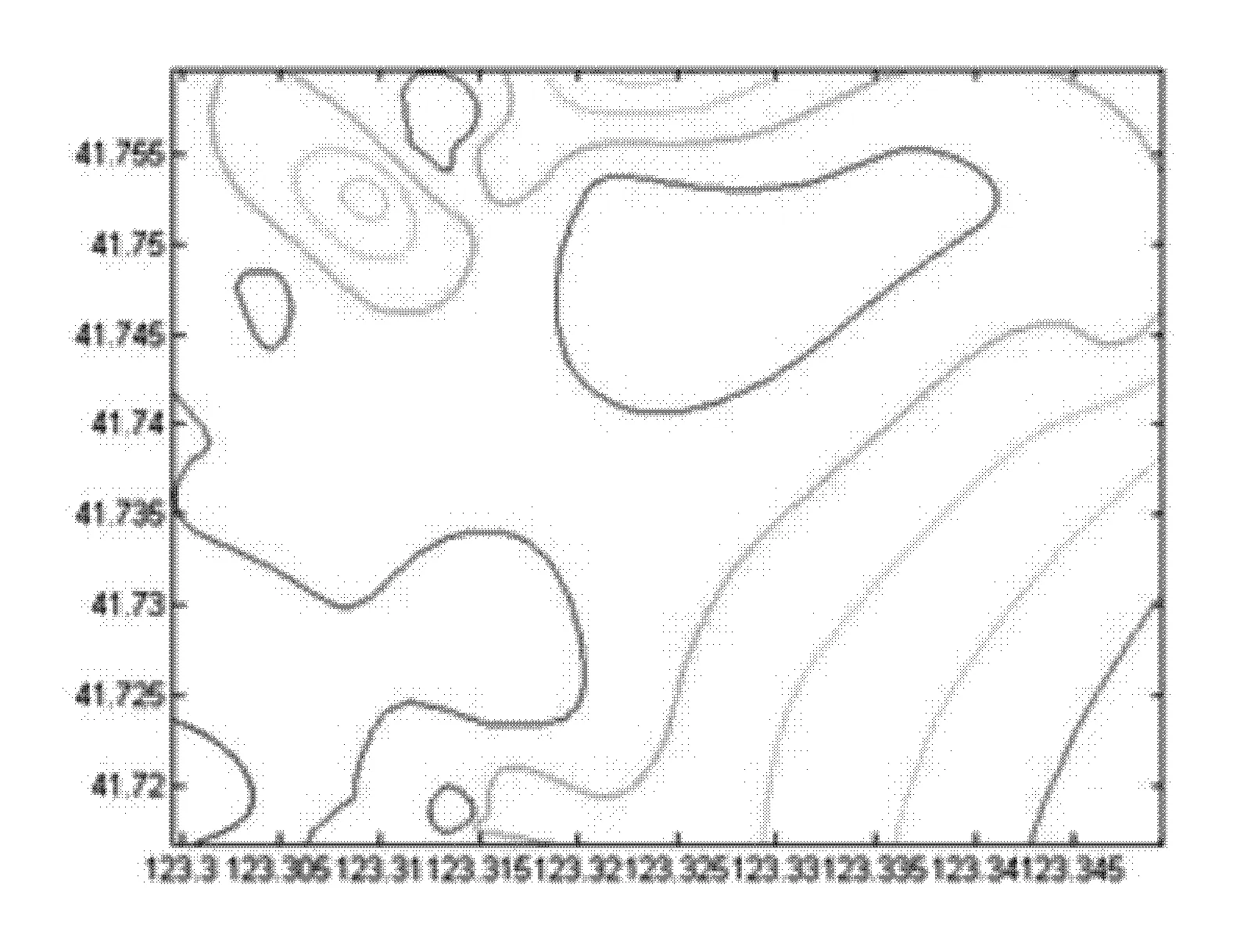
图2 研究区初始氨根浓度等值线图

图3 研究区初始浓度估计协方差等值线图

研究区2012年9月实测氨根浓度等值线图和估计协方差等值线图分别如图4和图5所示。

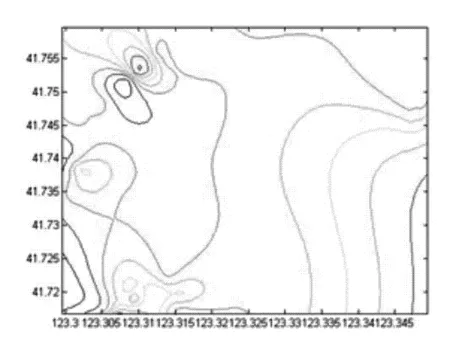
图4 实测氨根浓度等值线图

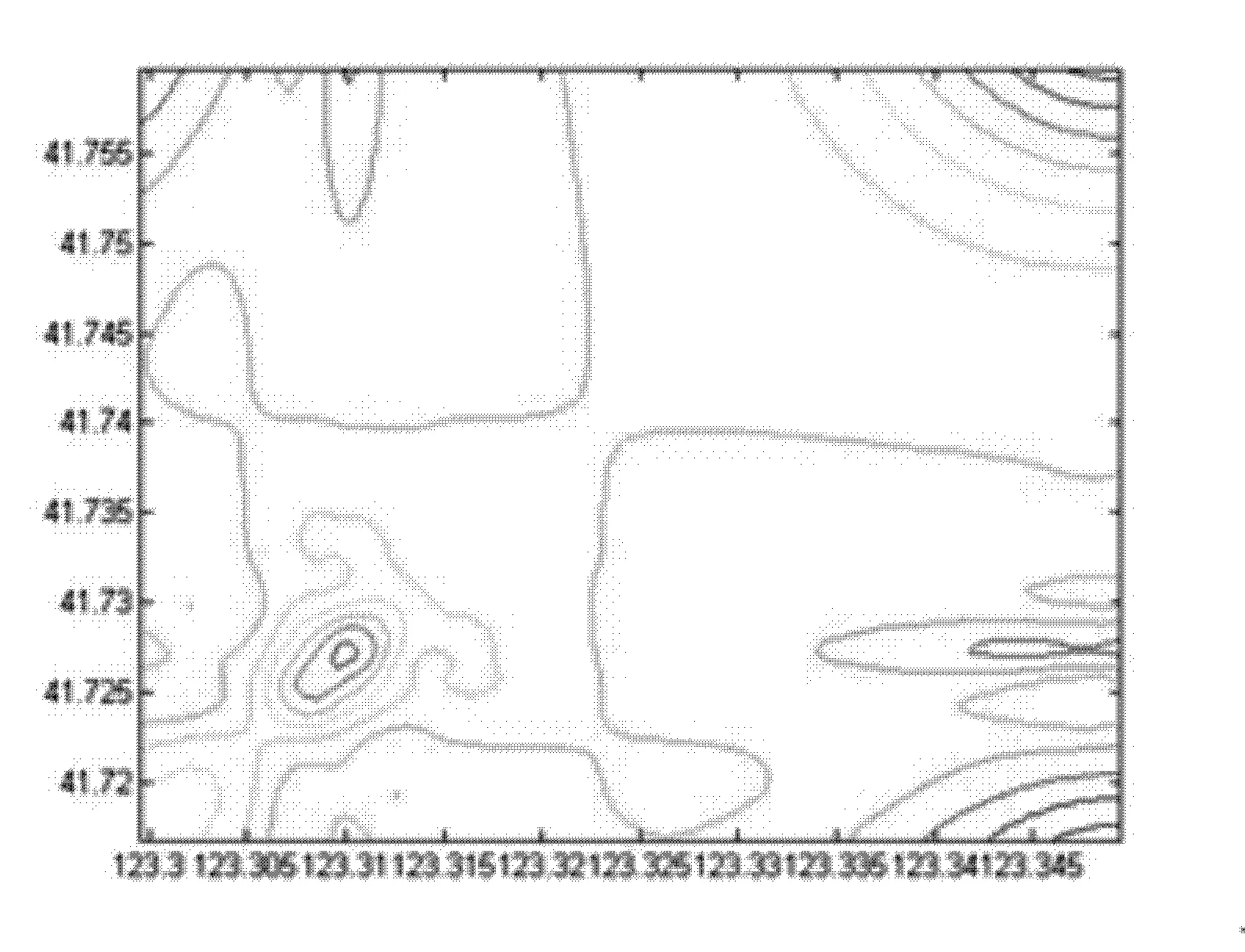
图5 实测氨根浓度估计协方差等值线图

研究区氨根浓度最优估计等值线图及估计误差协方差等值线图分别如图6和图7所示。

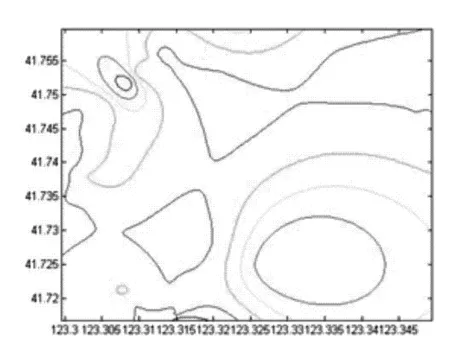
图6 研究区氨根浓度最优估计等值线图

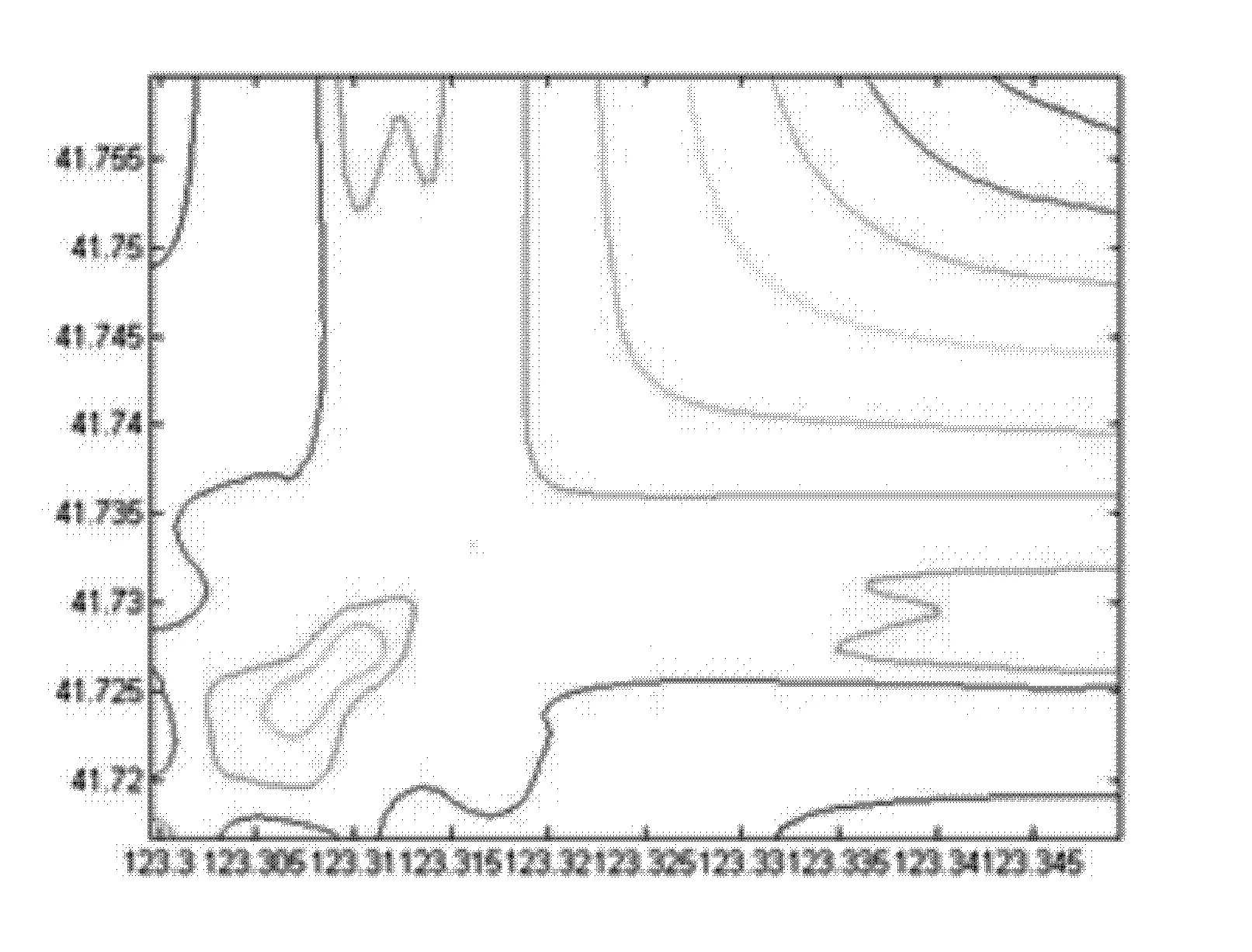
图7 研究区氨根浓度估计协方差等值线图

比较图4和图6，以及5和图7可以看出，通过有限差分卡尔曼滤波算法计算出的浓度场与实测浓度场基本吻合，可以反映研究区氨根离子的空间分布。

研究区部分采样点氨根浓度实测值与最优估计值比较如图8所示。

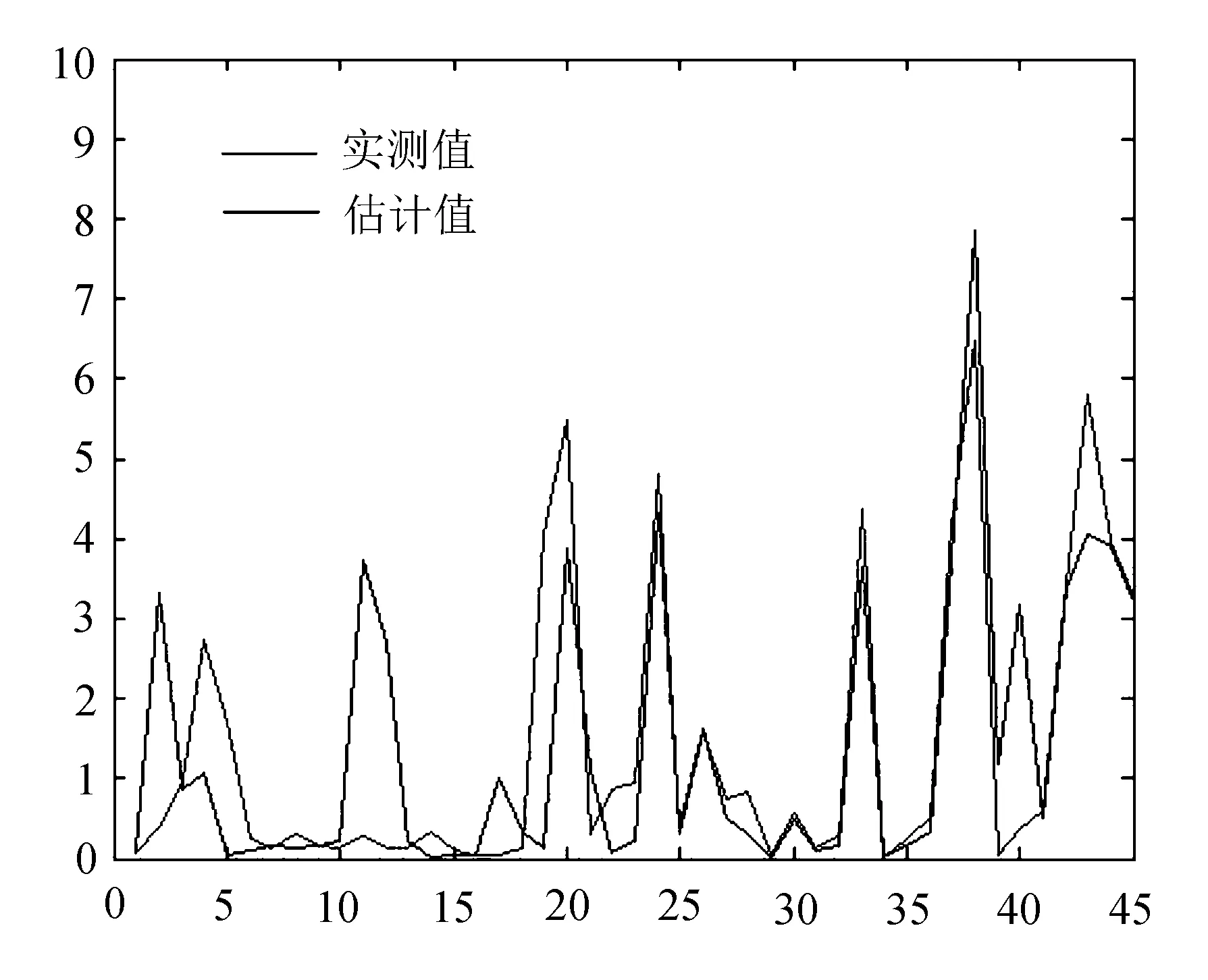
图8 研究区部分采样点氨根浓度实测值与最优估计值比较

从图8中可以看出，45个采样点中除2、4、11、12、40五个采样点拟合较差外,其余40个采样点的最优估计值与实际测量值拟合的比较好，可能由于观测精度或误差协方差过大引起的，但能表现出算法的可靠性。通过文中提出的有限差分卡尔曼滤波算法校正后的模型，基本能反映实际氨根离子在研究区的迁移转化特征，最优估计值与实际测量值拟合良好。

由图中可知，通过文中提出的有限差分卡尔曼滤波算法校正后的模型，基本能反映实际氨根离子在研究区的迁移转化特征，最优估计值与实际测量值拟合较好。

4 结 语

综合分析卡尔曼滤波算法的实际功能和地下水污染物运移的实际情况，文中提出一种基于有限差分改进的卡尔曼滤波算法联合估计地下水污染物运移模型的状态及相关参数的新方法，通过对辽河流域地下水污染物迁移转换问题的分析，验证了该方法在地下水污染物运移模型上的可行性，使监测数据得到充分利用，并且充分考虑到各种误差干扰，有效提高模型准确性。

[1] Hendricks Franssen H J,Kinzelbach W,Hendricks Franssen，et al. Real-time groundwater flow modeling with the ensemble Kalman Filter:Joint estimation of states and parameters and the filter inbreeding problem [J]. Water Resources Research,2008,44(9):108-128.

[2] 王昕.卡尔曼滤波在模型参数估计中的应用[D].哈尔滨：哈尔滨工业大学,2008.

[3] Assumaning G A，Chang S Y. Use of simulation filters in three-dimensional groundwater contaminant transport modeling [J]. Journal of Environmental Engineering，2012,138(11):1122-1129.

[4] 王新民,董小刚.计算方法简明教程[M].北京：科学出版社，2010.

[5] 孙永泉,刘梅侠,董学良,等.运用Kalman滤波技术校正地下水流系统确定-随机性数值模型[J].黑龙江水专学报,2010,37(1):110-114.

[6] 王广德,余芸生,贺宜达日.地下水可溶性污染物迁移的最优估算[J].环境科学学报，1988,8(4):385-392.

[7] Gharamti M E,Hoteit I. Complex step-based low-rank extended Kalman filtering for state-parameter estimation in subsurface transport models [J]. Journal of Hydrology,2014,509(4):588-600.

[8] 李波，王建帅，任媛，等.傍河型水源地水质预测解析解模型[J].长春工业大学学报：自然科学版，2012,33(3):245-249.

[9] 许可,陈鸿汉.地下水中三氮污染物迁移转化规律研究进展[J].中国人口：资源与环境,2011(S2):421-424.

Study on the estimation of pollutant transfer and transformation of pollutants in groundwater with finite difference Kalman filter——Application of the Liaohe River basin

WANG Xinmin,CHEN Huiying*,MA Xudong

(School of Basic Science,Changchun University of Technology,Changchun 130012，China)

Derivative is replaced with difference quotient in Finite difference method to deduce the transfer matrix of the Kalman filter for estimating the main pollutants,ammonia nitrogen migration and transformation. It provides some technical support for the Liaohe River basin management.

groundwater pollution; pollutant transfer; finite difference; Kalman filter.

2016-04-20

国家自然科学基金资助项目(51278065)

王新民(1957-)，男，汉族，山东牟平人，长春工业大学教授，博士，主要从事水环境系统正反问题数学模型与数值方法研究,E-mail:wxm@jlu.edu.cn. *通讯作者：陈慧颖(1991-)，女，汉族，黑龙江双鸭山人，长春工业大学硕士研究生，主要从事水环境系统正反问题数值模拟方向研究,E-mail:8497871436@qq.com.

O 242

A

1674-1374(2016)05-0417-05