随车吊机械臂运动学建模及逆运动学求解

任晓琳

(长春工业大学 电气与电子工程学院，吉林 长春 130012)



随车吊机械臂运动学建模及逆运动学求解

任晓琳

(长春工业大学 电气与电子工程学院，吉林 长春 130012)

根据随车吊机械臂各关节的运动特点，详细分析机械臂的运动学模型,采用齐次变换矩阵推导出系统的正运动学方程。针对随车吊机械臂逆运动学存在多解的问题，提出了一种基于改进收缩扩张因子的量子粒子群优化算法，并在算法中加入混沌搜索抑制“早熟”问题。仿真结果验证了机械臂逆解计算的有效性。

随车吊；逆运动学；量子粒子群；混沌搜索

0 引 言

随着工业自动化的发展，各行各业对机械设备自动化程度的要求也越来越高。机器人技术的快速发展，使智能化不断提高，而机器智能化不仅体现在先进的智能系统，也包括机器人本体机构特性的智能化。冗余机器人由于其自身结构具有较高的灵活性，再次受到研究者们的关注，并已成为机器人技术发展的一个重要方向。

随车吊是一个8自由度关节式机械臂，其运动学模型不仅是几何结构分析的基础，也是关节速度和加速度分析的基础。当前，机械臂运动学模型通常采用D-H参数法建立，其优点是便于进行雅克比矩阵的分析，但是在复杂的多关节的机械臂模型中，例如系统中存在回转、旋转、拉伸等多个关节时，机械臂不仅在x和z轴上运动，也有y轴上的运动，此时D-H参数法在关节坐标的设定上较为复杂。

另外，机械臂正向运动的解唯一且确定，逆向运动的解往往不唯一。简单结构的机械臂通常选择分离变量法[1-2]和几何法[3]，通过解析的方式得到逆运动学解；而机构尺寸较为复杂的机械臂需要借助数值迭代的方法求取运动学的逆解，但是迭代法运算速度慢，不适用于工业机械臂的实时控制。越来越多的学者采用智能控制算法解决逆运动学问题。Wu[4]提出了微分进化算法计算冗余机械臂的运动学逆解，并与传统的解法相比较，验证了该算法的有效性。任子武[5]等采用和声搜索算法解决7自由度冗余机械臂的逆运动学问题，该方法不仅提高了算法的全局寻优性能,并且提高了所求解的可靠性。曹俊琴[6]等针对BP神经网络算法的缺点，把思维进化算法引入神经网络的网络权值计算中，该方法收敛速度快，且提高了计算精度。芮挺[7]等利用模拟退火粒子群优化算法在解空间中高效的搜索能力，直接从正运动学方程出发求解机器人关节变量。

文中以8自由度随车吊机械臂为研究对象，根据随车吊结构特点，采用齐次变换矩阵的方法建立系统的正运动学方程，在此基础上采用量子粒子群优化算法计算运动学逆解。首先引入Logistic映射初始化粒子群，提高初始种群的多样性，其次根据文献提出的聚集距离变化率改进算法中的收缩扩张因子，提高算法的搜索能力，最后为了避免出现早熟，将混沌映射再次引入QPSO算法中进行优化搜索，以提高全局搜索能力，跳出局部最优值。该方法利用量子粒子群优化算法运算简单、需要参数少、收敛速度快和混沌优化算法易跳出局部极小值、计算精度高等优点，为实现机械臂的运动控制奠定基础。

1 机械臂结构描述

随车吊机械臂的液压系统由定量泵、支腿油缸、变幅油缸、折叠油缸和伸缩油缸等组成，其机械结构包括基座、折臂、伸缩臂、吊具等组成。其中，伸缩臂采用三节顺序伸缩，伸缩油缸选择内置式磁致伸缩传感器，可实现精确的伸缩量控制和反馈。随车吊机械臂吊具的整个操作过程无需使用辅助元件，属于纯机械作业的机构。同时，为了避免机械臂在抓取物体时的刚性碰撞，吊具采用刚柔耦合的机构设计，当机械臂抓取包装箱时，吊具接近箱体上方，刚柔转换机构从刚性转换到柔性，底部机构滑入箱体卡槽内，并进行卡死操作；提升箱体时，刚柔转换机构从柔性变回刚性，然后进行提升作业。其结构如图1所示。

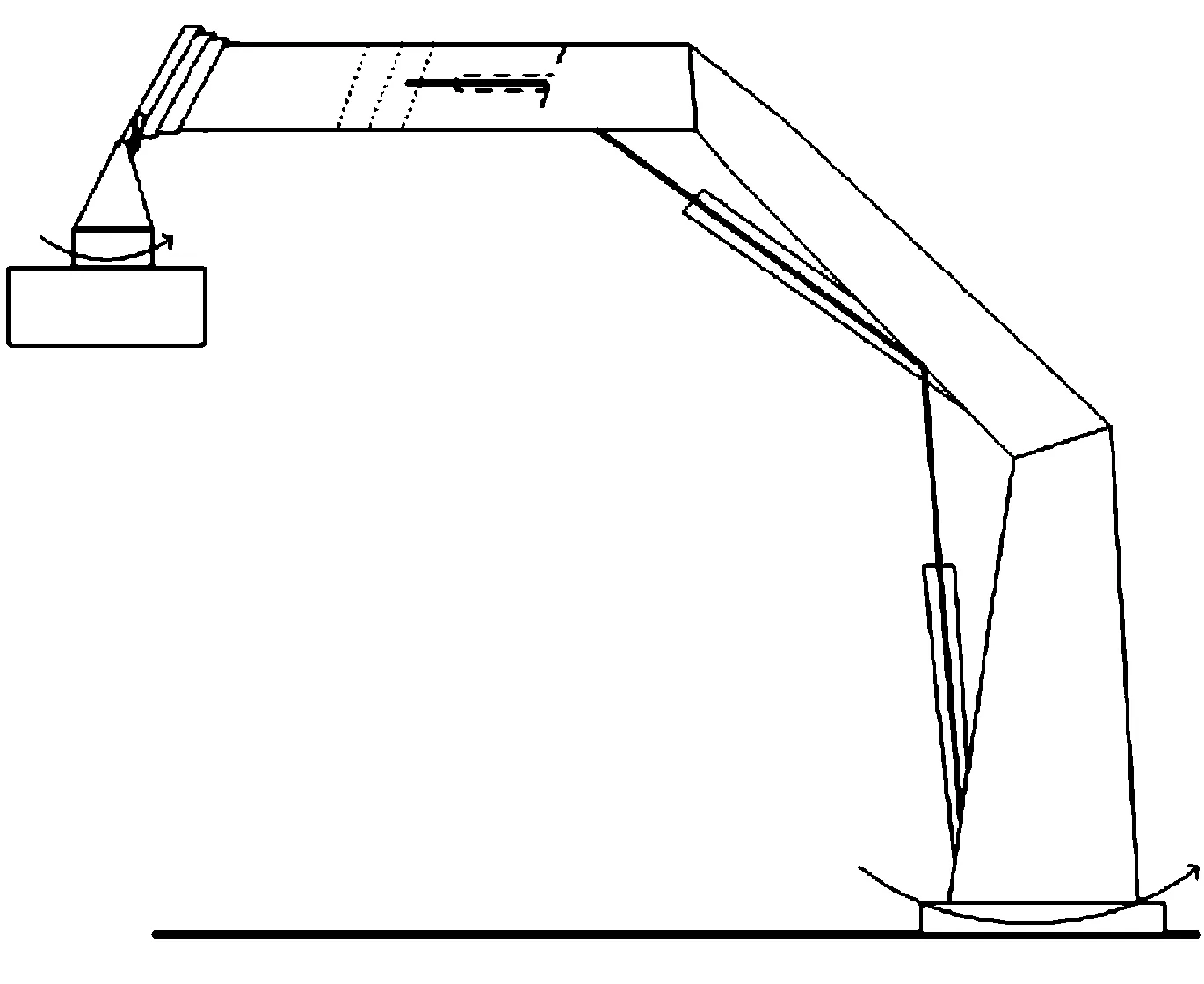
图1 随车吊机械臂结构示意图

2 随车吊运动学方程建立

随车吊机械臂各关节坐标系如图2所示。

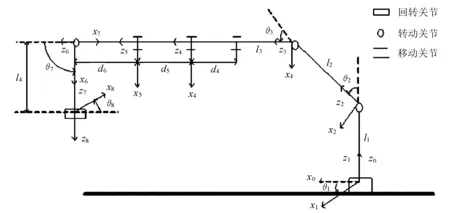
图2 随车吊机械臂各关节坐标系

根据随车吊轴向运动特点，规定各个关节坐标系的方向如下[8]：连杆的方向为z轴，x轴定义为垂直于z轴的方向，y轴根据右手定则确定。参考坐标系{0}与基座坐标系{1}重合，即z0轴与连杆1轴线重合。根据各关节坐标系(见图2)可知，基座绕连杆l1的z轴旋转θ1，关节2绕连杆l2的y轴旋转θ2，关节3绕连杆l3的y轴旋转θ3，3个伸缩连杆沿z轴方向伸长d4、d5、d6，关节7绕连杆l4的y轴旋转θ7，关节8绕z轴旋转θ8，相应的各个关节的位姿变换矩阵如下：

正运动学方程为：

其中

根据作业要求，随车吊在抓取包装箱时末端姿态是确定的，它要求包装箱要垂直向下，因此要保持吊具杆与水平位置垂直，即α=180°(α=θ2+θ3+θ7)；吊具抓(或放)箱体都要保证其摆放的方向性，为保证吊具卡槽对准抓物体的姿态，因此为了控制吊具抓物体的姿态，θ8是机械臂吊具姿态角，即β=0°(β=θ1-θ8)。另外，文中3个伸缩连杆采用顺序伸缩方式，首先伸长d6，然后伸长d5，最后伸长d4，伸缩连杆可按照如下方式变化：

从作业约束中不难发现，机械臂在运动过程中姿态保持不变，因此θ7和θ8从运动学方程中解耦出来；3个伸长连杆根据伸缩方式合并为1个伸长变量D。此时随车吊结构中含有4个自由度，即θ1、θ2、θ3和D，但运动学模型中仅有3个方程。机械臂存在冗余自由度，这种情况下，若不加其它约束条件，随车吊的逆运动学存在无穷多组解。

3 逆运动学优化算法

3.1 量子粒子群算法简介

量子粒子群算法(Quantum-behavedParticleSwarmOptimization，QPSO)是孙俊[9]等从量子力学原理出发提出的一种改进的粒子群优化(ParticleSwarmOptimization，PSO)算法，与标准PSO算法不同，粒子的运动状态不是由粒子的位置和速度表示，而是通过模拟量子力学中粒子在势场中向势能最低点的移动，即将粒子解空间视为量子力学中的势场(势阱)，将粒子寻优过程视作势场中粒子向势能最低点的移动过程[10]。文中采用δ势阱模型，将粒子逐渐吸引到全局最优解。QPSO的基本公式如下：

(1)

(2)

(3)

(4)

式中：pbesti——第i次迭代的个体最优位置;

gbest——全局最优位置;

Pi——吸引子;

r,w——结余0到1之间的随机数;

Xi——粒子位置;

Mbest——个体平均适应度;

N——种群数量;

β——收缩扩张因子;

Tmax——最大迭代次数;

t——当前迭代次数。

3.2 改进量子粒子群优化算法

在QPSO算法中，收缩扩张因子是算法的搜索半径，它直接影响算法的性能及收敛速度，一般采用从1到0.5线性递减的方式。这种方式收缩扩张因子表现为只压缩非扩张，当算法前期找到最优解时，β值过大，搜索半径过大可能出现跳出最优值的情况，从而降低搜索能力。当量子在运动中遇到局部极值，而收缩扩张因子递减会降低搜索能力，从而使算法陷入局部最优[11-12]。为了改善QPSO算法，文中以聚焦距离变化率为判别标准对收缩扩张因子进行自适应调整，并引入混沌映射提高粒子的全局搜索能力，避免出现早熟问题。

3.2.1 改进的收缩扩张因子

引入文献[13]定义的聚焦距离变化率k，根据每次迭代计算的k值判断当前粒子的搜索能力，并自适应调整收缩扩张因子。

当前粒子的聚焦距离变化率为：

(5)

根据k值的变化，采用自适应非线性递减函数代替式(4)线性变化的收缩扩张因子，其表达式为：

(6)

其中，α1=0.3，α2=0.2，r为介于0至1的随机数。

3.2.2 混沌粒子群优化算法

混沌搜索具有随机性和遍历性的特点，能在一定范围内按其自身的“规律”不重复遍历所有状态，实现全局最优[14]。文中采用典型的Logistic混沌映射建立初始种群，当Logistic映射的控制参数为4时，所描述系统完全处于混沌状态，实值序列zk如下式：

(7)

按照混沌量子粒子群优化算法的思想，首先按照Logistic映射搜索建立初始种群，通过该载波方式在解空间中建立较均匀的种群序列，提升粒子的初值敏感度；然后进行量子粒子群算法的基本操作，当粒子进入局部收敛，即出现“早熟”，引入混沌搜索，提高全局搜索能力，跳出局部最优,使其快速收敛到全局最优解。

3.3 算法流程

步骤1：初始化设置相关参数，如最大迭代次数、种群数量、粒子维数、混沌搜索次数等；

步骤2：在解空间利用混沌映射生成初始量子种群；

步骤3：计算粒子适应度值；计算粒子所经历的最好位置pbest和群体中经历的全局最优位置gbest；

步骤3：根据式(5)和式(6)确定出自适应收缩扩张因子的值；

步骤4：根据式(2)更新粒子，并计算更新后的所有粒子的适应度值，若粒子适应度优于pbest的适应度，则设为pbest，在pbest中选择适应度最优的个体设为gbest；

步骤5：判断算法是否满足终止条件，若满足，则转向步骤8,若不满足则执行步骤6；

步骤6：计算群体适应度方差和平均粒距，判断是否进入局部极值，若成立，则进行步骤7，否则转向步骤3；

步骤7：重新进行次混沌搜索，计算其适应度值，得到性能最好的可行解，用取代群体中最后一个粒子的位置，转到步骤3进行下一次量子粒子群算法；

步骤8：结束进化过程，输出全局最优解。

4 仿真实验及分析

针对随车吊机械臂的逆运动学各个关节变量求解问题，选取随车吊模型参数为：l1=1 740mm，l2=2 500mm，l3=3 000mm，l4=800mm；设定任意指定状态的随车吊机械臂的末端位置，采用标准量子粒子群和改进的混沌量子粒子群算法进行比较，这里改进的量子粒子群优化算法中的收缩扩张因子采用式(6)的自适应调整函数，并且加入早熟判定。实验中将位置误差作为算法的适应度函数，设初始种群为100，最大迭代次数为300，混沌搜索最大次数为50。

在同一初始种群下，比较算法的寻优效果，这里给出一个位置向量(1.171 9,4.221 4,2.477 4)。实线为具有自适应β因子的CQPSO算法，虚线为具有自适应β因子的QPSO算法，点划线为标准QPSO算法,各种算法比较结果如图3所示。

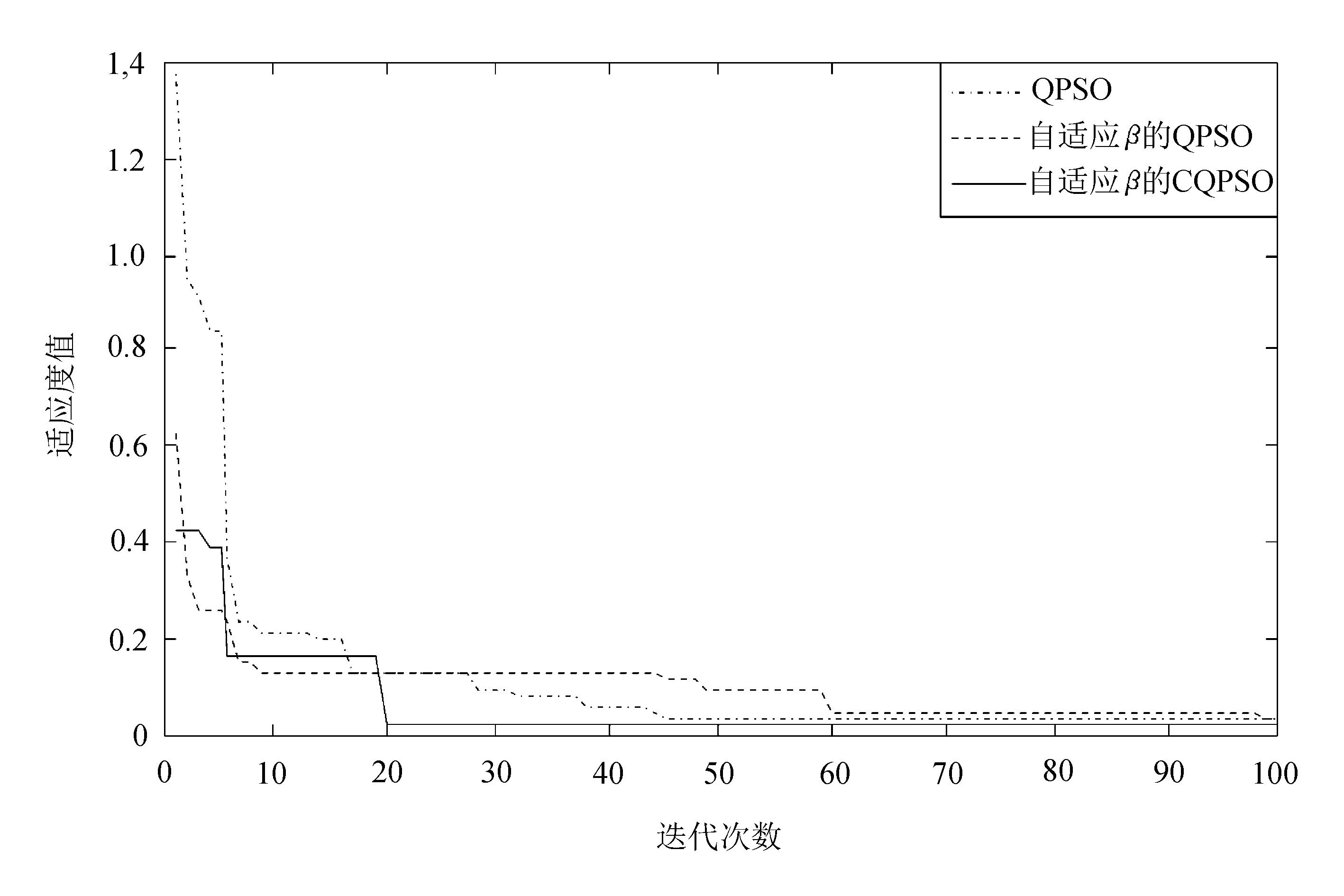
(a) 全部算法收敛到全局最优解

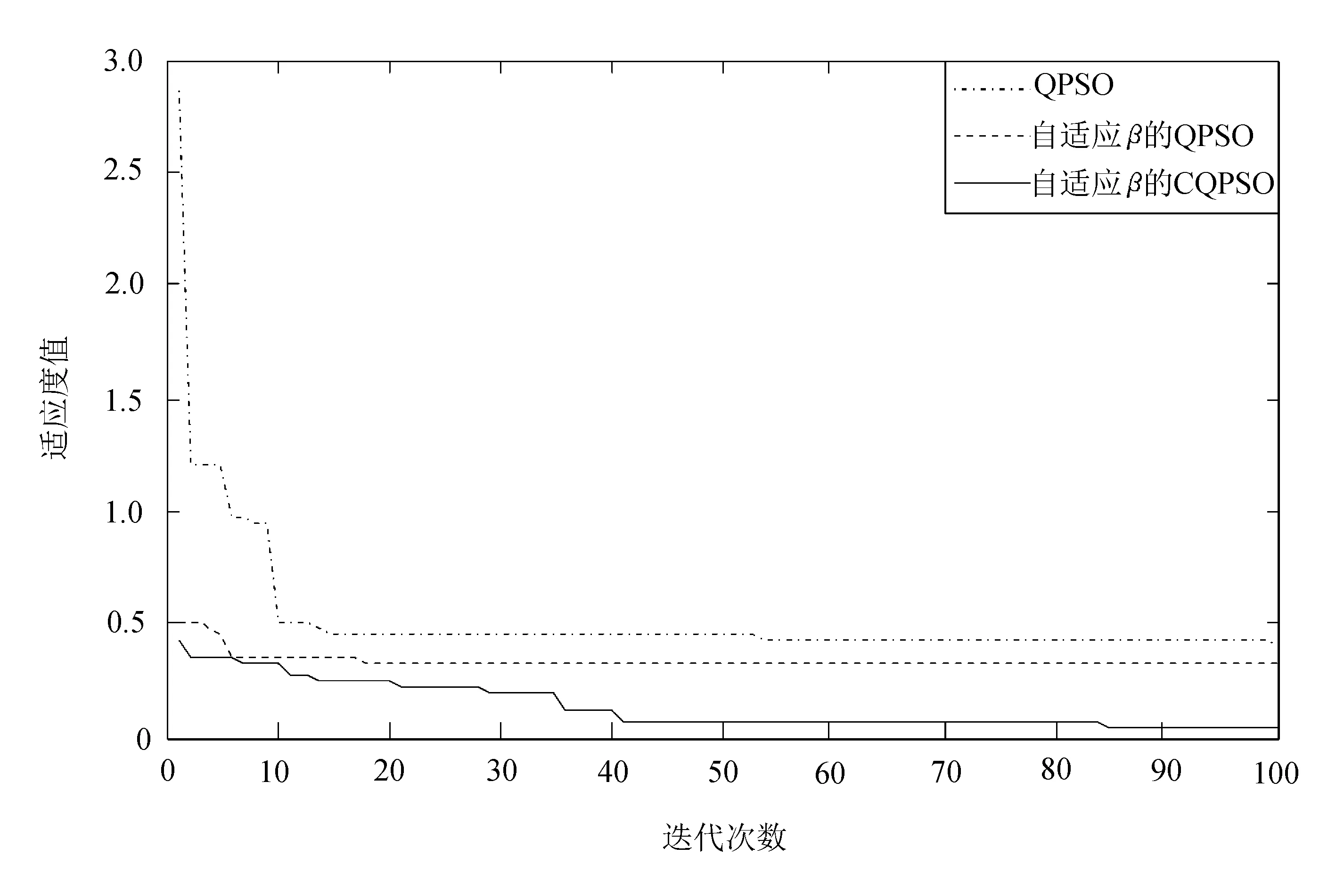
(b) 部分算法收敛到局部最优解

图3 各种算法比较结果

从图3(a)中可以看出,3种算法都能收敛到较好的适应度值；图3(b)中相比QPSO算法和带自适应β因子的QPSO算法，带自适应β因子的CQPSO算法能跳出局部极值得到全局最优解。

选取工作空间的任意3组位置向量分别进行100组测试，由于标准粒子群算法没有对局部收敛和早熟进行处理，导致其平均适应度值和平均误差都比较大；加入早熟判定后，CPSO算法得到的平均适应度值和位置误差优于改进的PSO算法。因此，CPSO具有较好的寻优能力和搜索精度。搜索效果比较见表1。

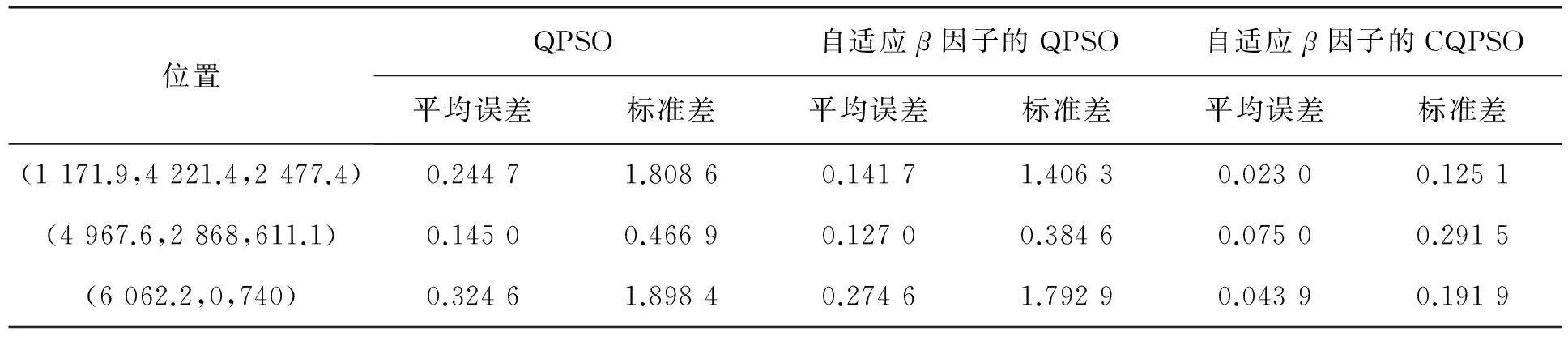
表1 搜索效果比较

5 结 语

分析了随车吊机械臂的结构及运动特性，采用齐次变换矩阵的方法建立了系统的正运动学模型，通过对作业任务的约束，对机械臂部分关节进行解耦。针对解耦后冗余机械臂的逆运动学问题，采用具有自适应β因子的CQPSO算法，选取位置误差作为适应度函数，得到一组可行的逆运动学解。在Matlab仿真中，通过仿真比较了几种算法的优化效果，其结果表明了该算法的有效性。

[1] 周国义，谢明红，孙友生，等.6自由度解耦机器人运动学逆解优化的研究[J].机电产品开发与创新，2009，22(5)：21-23.

[2] 王其军,杜建军.MOTOMAN机器人逆运动学新分析[J].哈尔滨工业大学学报，2010，42(3)：451-454.

[3] Samer Yahya,Haider A F，Mohamed Moqhavvemi M,et al. A new geometrical inverse kinematics method for planar hyper-redundant manipulators[C]//Innovative Technologies in Intelligent Systems and Industrial Applications.2009:20-22.

[4] Wu H,Handroos H. Inverse kinematics analysis of a parallel redundant manipulator by means of differential evolution [C]//Human Friendly Mechatronics.2001:321-326.

[5] 任子武,王振华,孙立宁.全局和声搜索方法及其在仿人灵巧臂逆运动学求解中的应用[J].控制理论与应用,2012,29(7):867-876.

[6] 曹俊琴，冯佳鹏，张春美.一种基于思维进化算法的神经网络求解机器人逆运动学问题[J].电脑开发与应用，2008,21(4)：30-32.

[7] 芮挺，朱经纬，蒋新胜，等.PUMA机器人逆运动模拟退火粒子群求解方法[J].计算机工程与应用，2010，46(3)：27-29.

[8] 李元春，任晓琳.随车吊机械臂的吊装轨迹规划方法[J].长春工业大学学报：自然科学版,2012，33(5)：543-547.

[9] Sun J,Feng B,Xu W B. Particle swarm optimization with particles having quantum behavior[C]//Proceedings of 2004 Congress on Evolutionary Computation.Piscataway. N J:IEEE Press，2004:325-331.

[10] 李盼池,王海英,宋考平,等.量子势阱粒子群优化算法的改进研究[J].物理学报,2012,61(6):60302-60309.

[11] 郭蕴华,王晓宗.基于改进量子粒子群算法的无人机路径规划[J].船海工程,2016(1):99-102.

[12] 关学忠,皇甫旭,李欣,等.基于正态云模型的自适应变异量子粒子群优化算法[J].电子设计工程,2016,24(8):64-67.

[13] 任子晖,王坚.一种动态改变惯性权重的自适应粒子群算法[J].计算机科学,2009,36(2):227-229.

[14] 申清明,阎立军.基于混沌搜索的特征选择方法[J].兵工学报，2013，34(12)：1616-1619.

Kinematics modeling and inverse kinematics solution for an onboard craning manipulator

REN Xiaolin

(School of Electrical & Electronic Engineering,Changchun University of Technology,Changchun 130012，China)

According the motion characteristics of each point in an onboard craning manipulator,we analyze the kinematics model of the manipulator and deduces the forward kinematics equation with via homogeneous transformation. To solve manipulator inverse kinematics problems,a quantum particle swarm optimization(QPSO) algorithm is proposed based on adaptive contraction-expansion coefficient. The algorithm is improved by adding chaos search to check the premature convergence. Simulation results verify the algorithm.

onboard craning manipulator; inverse kinematics; QPSO; chaos search.

2016-05-26

国家自然科学基金资助项目(61374051); 吉林省科技发展计划基金资助项目(20150520112JH)

任晓琳(1985-)，女，汉族，吉林长春人，长春工业大学助理实验师，中国科学院长春光学精密机械与物理研究所博士研究生，主要从事智能机械与机器人控制方向研究,E-mail:xlren1885@ccut.edu.cn.

10.15923/j.cnki.cn22-1382/t.2016.5.08

TP 273

A

1674-1374(2016)05-0454-07