基于HLM2的算例分析及其在中国非寿险精算中的思考

孙维伟，张连增

（1.天津理工大学管理学院，天津300384；2.南开大学 金融学院，天津300350）

基于HLM2的算例分析及其在中国非寿险精算中的思考

孙维伟1，张连增2

（1.天津理工大学管理学院，天津300384；2.南开大学 金融学院，天津300350）

随着保险业务的拓展和深化，财产保险中越来越多地出现具有相关性和层次性的保险数据。分层线性模型对此类数据的处理能充分地体现在数据的分析中，在国际精算领域中的应用处于起步阶段。文章分析了分层线性模型具有二层、三层结构的数据特点，采用线性混合模型和分层线性模型方法，完成了二层结构数据的模型构建、实现与比较。

相关数据；分层数据；非寿险费率厘定；线性混合模型；分层线性模型

0　引言

广义线性模型（GLM）在诸多国家的非寿险定价实务中的长足发展，引发国内外学者对其拓展类的研究。Smyth(1989)对GLM的假设加以改进，假定广义线性模型中的离散参数不再是常数，其经变换后可以表示为解释变量的线性形式，从而提出了双广义线性模型（Double Generalized Linear Models，DGLM）。Hastie和Tibshirani(1990，1993)将非参数光滑技术应用于指数散布族分布，并使用非参数、半参数结构代替GLM中的线性预测量，将其扩展为广义可加模型（Generalized Additive Models，GAM）。在统计学中为处理有相关性和层次性的数据，较早的模型是线性混合模型（Linear Mixed Models，LMM），继而出现广义线性混合模型（Generalized Linear Mixed Models，GLMM）、分层广义线性模型（Hierarchical Linear Mixed Models，HGLM）。这些具有固定效应和随机效应的模型已应用于心理学、教育学、环境科学、生态学和社会学等多个领域，而其在保险领域的应用已是当前国际精算理论研究的热点。

1　数据类型与模型理论基础

1.1数据类型描述

1.1.1相关数据

相关是指两个或两个以上变量（两组或者两组以上数据）之间相互关系的程度或强度[1]，按照强度包括完全相关、高度相关（强相关）、弱相关和零相关四种情况。此外，宏观经济中的时间序列和经济计量模型中的随机误差序列常常存在着自相关。自相关是相关关系的一种，又称序列相关，原指随机变量在时间上与其滞后项之间的相关，也指回归模型中随机误差项与其滞后项的相关。若随机项ui存在自相关，则有cov(ui，uj)≠0，(i，j∈T，i≠j)。在非寿险精算学中，具有相关结构的数据是很常见的，譬如，同一份保单在多个投保期内的损失数据往往具有相关性。

纵向数据、空间聚类数据、甚至更一般的聚类数据都是存在相关性从而不满足独立性的数据结构的例子。纵向数据在计量经济学中常被称为面板数据，与时间序列数据、截面数据构成计量经济学三种主要数据类型。纵向数据可以视为时间序列数据与截面数据的混合，包含截面和时间二维特征。例如，投保人往往是连续多年投保，损失数据具有时间序列特征；同时，由于不同地区的地理条件等差异，导致各地区内的投保人索赔行为具有地区差异。随着大数据时代的发展，纵向数据在非寿险精算学中日益增加。

1.1.2分层数据

分层数据（hierarchical data）最初常见于社会与行为学中。所谓分层，也称阶层，是由较低层次观察数据嵌套在较高层次之内的数据结构所组成。其中，最低层次的测量称为微观层次，其他高层次的测量则属于宏观层次，宏观层次通常由不同的组别构成[2]。个体处于不同的组（团体），有些变量与个体有关，有些变量与团体有关。例如，学校收集的学生资料包含性别、种族、学习态度与家庭环境等用于描述学生特征的变量，也可以包含反映学校特征的变量，如学校类型和地点等。针对上述数据，学校可以作为宏观分析单位，学生作为微观分析单位，学生嵌套于学校范围内，形成一个具有二层观测数据的数据集。此类二层数据结构还可以拓展到三层甚至更多的层级，如学生嵌套于班级、学校、地区、国家等。

随着保险大数据的不断出现，多层次数据结构在非寿险业务中日益增多，如费率厘定与准备金评估中索赔或损失数据已经出现分层结构，对这些分层数据的收集、整理与精准分析对保险市场发展具有重要的理论与现实意义。

1.2LMM和HLM的基本理论

1.2.1LMM的基本理论

LMM的发展历史可以追溯到1861年，最早出现的形式是单因素随机效应模型，20世纪90年代以后成为医学和社会科学中广泛使用的统计模型，在这些学科中也被称为多层次模型（multilevel models）或分层线性模型[3]。假设要分析的数据由N个对象的观测值组成，第i个（1≤i≤N）对象（个体）的观测次数是ni。Yi=(Yi1，Yi2，…，Yini)′表示第i个对象的ni×1维的观测向量，LMM可表示为：

1.2.2HLM的基本理论HLM的概念最早由Lindley和Smith(1972)[4]提出，HLM的基本思想在于：在特定的数据结构中，模型的某些参数本身需要建模，依据数据的不同层次设置不同水平，将回归系数进行相应分解，可以视为“回归的回归”。HLM的特点是不需要假设观测数据是否相互独立，可以同时对个体水平（微观层次）和组群水平（宏观层次）的数据进行分析，把复杂的问题分解为相互联系的各个组成部分，为科学研究提供一种新的概念框架。HLM可以有二层、三层、四层甚至更一般结构的发展模型，更可以拓展为HGLM（Lee和Nelder，1996[5]）。本文仅以二层结构的HLM（简记为HLM2）为例对其理论进行简要分析。

最简单的二层结构HLM等价于带随机效应的单因素方差分析，基本形式为[6]：

将β0j的表达式代入Yij中，得到：

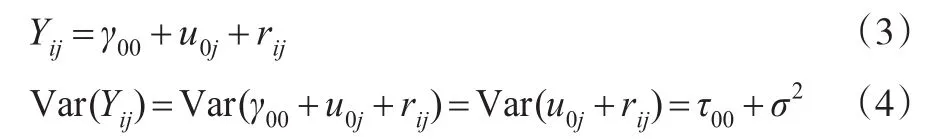
其中，Yij代表被解释变量，β0j是第一层模型的截距，γ00是第二层模型的截距，随机变量rij满足 E(rij)=0，Var(rij)=σ2，u0j满足Var(u0j)=τ00。方差σ2代表组内变化，方差τ00代表组间变化。组内相关系数（Intraclass Correlation Coefficient，ICC）定义为[7]：

ICC是指组间方差占总体方差的比例，可以测量总体变异中由于第二层的差异造成的变异比例。将式（2）进行拓展，简单的HLM的基本形式包括三个表达式：

式（6）中包含以下三类参数：

①固定效应γ00和γ10，它们分别是 β0j和 β1j的平均值，在第二层的单位之间是固定的；

②随机效应u0j和u1j，它们分别是随机的第一层系数β0j和β1j的随机成分，代表第二层单位之间的变异；

③方差协方差成分：

进一步地，在回归系数中引入被解释变量，更一般的二层HLM模型可以表示为：

将式（8）中β0j和β1j的表达式依次代入Yij的表达式，得到：

此时，Xij表示第一层的解释变量，rij是第一层的随机变量，Wj表示第二层的解释变量，γ00，…，γ11是第二层的系数称为固定效应，u0j和u1j是第二层的随机变量，这里假设：

2　基于HLM2的算例分析

2.1数据来源及说明

非寿险精算中已经出现分层次结构的数据，然而，经调研表明，中国保险业公开数据源（如历年《中国保险年鉴》、保监会官网、各大保险公司年度报告）鲜有相关数据类型，中国各地区不同投保人多年的索赔数据尚未公开。局限于现阶段保险实务中的分层数据较难获取，本文仅以R软件WWGbook程序包中的一组ratpup数据为样本进行算例分析，该组数据也见于West等(2007)。虽然数据方面无法揭示非寿险数据特征，但是模型对数据的分析过程及思想可以延展，期待国内数据完善后推广应用到中国保险业。ratpup数据以实验幼鼠为标本，随机分配一种特定的高、低或是标准水平的药物剂量，通过比较接受高剂量和低剂量处理的雌性大鼠所生的每窝幼鼠与接受标准剂量处理的雌性大鼠所生的每窝幼鼠的出生体重来研究药物的剂量水平、性别等因素如何影响幼鼠出生时的体重。该组数据属于看作二层结构的分层数据，幼鼠和窝作为分析单位，幼鼠嵌套在窝内，各变量是在两个层次分别进行测量的，包含6个变量的322个观测数据。各变量的定义及统计特征描述见表1。

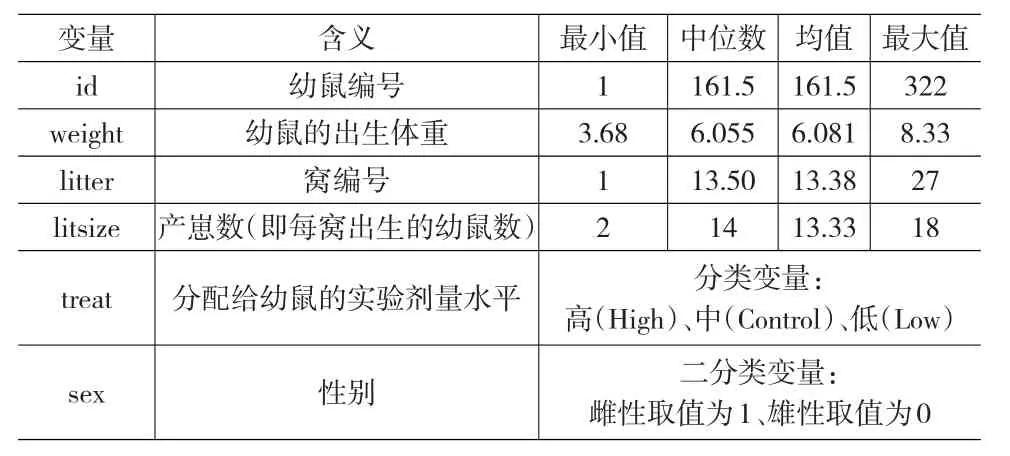
表1　变量含义及统计特征描述

2.2算例分析

2.2.1HLM2模型的建立

针对该组数据的特点建立分层模型进行算例分析，采用二层的分层线性模型来比较分配到三种不同剂量的窝幼鼠的平均出生体重，考虑了窝与窝之间的差异性，以及同一窝幼鼠之间的变异。在第一层模型中，对于大鼠的幼鼠这一分析单位而言，同一窝的剂量水平和幼鼠数是相同的，幼鼠的体重因性别而不同。以weight为被解释变量，sex为解释变量建立第一层模型（10）；在第二层模型中，首先设定参数 β0j和 β1j，进而需要合理解释使得 β0j和 β1j在所研究的特定问题背景中变得更有现实意义。

第一层模型：

β0j是截距项，β1j是变量sexij的斜率，下标i和 j代表的是第一层的个体i所隶属的第二层单位 j。weightij表示在第 j窝的第i个幼鼠的出生体重，其与幼鼠的性别相关。sexij是指示变量，雌性时sexij取值为1，雄性时sexij取值为0。第一层模型中随机变量rij是模型的残差，满足E(rij)=0，Var(rij)=σ2，体现同一个窝内的幼鼠之间的相关性。

第二层模型：

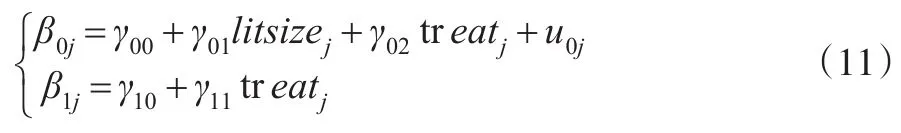
在第二层分析数据中，β0j与每一窝的幼鼠数litsizej和剂量水平treatj相关；β1j在第一层中用于描述在第 j窝的幼鼠i的出生体重weightij与其性别sexij之间的关系，在不同窝之间其与剂量水平treatj相关。γ00与γ10在第二层各单位之间是固定的，γ01、γ02、γ11分别是式（11）中回归方程的斜率，u0j是第二层模型的残差，第二层模型体现了不同窝内的未观测到的特征导致幼鼠的异质性。值得一提的是，由于treat是分类变量，而数据集默认中等剂量水平为基础组，因此该变量对应的待估参数事实上是两个，即γ02（高剂量水平）和γ02（高剂量水平）；sex作为二分类变量，将雄性作为基础组，因此该变量对应的待估参数为一个。

将式（11）中的 β0j和 β1j的表达式代入式（10），得到混合模型如下：

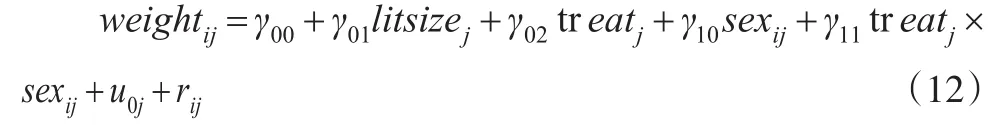
式（12）在形式上符合LMM的标准形式。其中，固定效应是截距项γ00、litsize所对应的γ01、treatj所对应的γ02、sexij所对应的γ10、treatj与sexij的交互效应所对应的γ11，也包含γ11（高剂量水平）和γ11（高剂量水平），随机效应是第二层的随机变量u0j和残差rij。

2.2.2基于HLM软件的实现

目前，分层线性模型的计算问题可以通过不同软件来解决，其中由Scientific Software International公司出品的HLM软件是一种较具针对性的软件。如果分层数据可以用第一层数据和第二层数据分别单独存储，使用该软件进行方便地分析，而R软件只能分析第一层数据和第二层集成为一个数据集的分层数据。将HLM（版本7.0）与R软件（版本3.13）进行比较，有利于对数据分析过程与结果的理解。

基于HLM软件，第一层和第二层模型的固定效应的参数估计结果如表2所示。

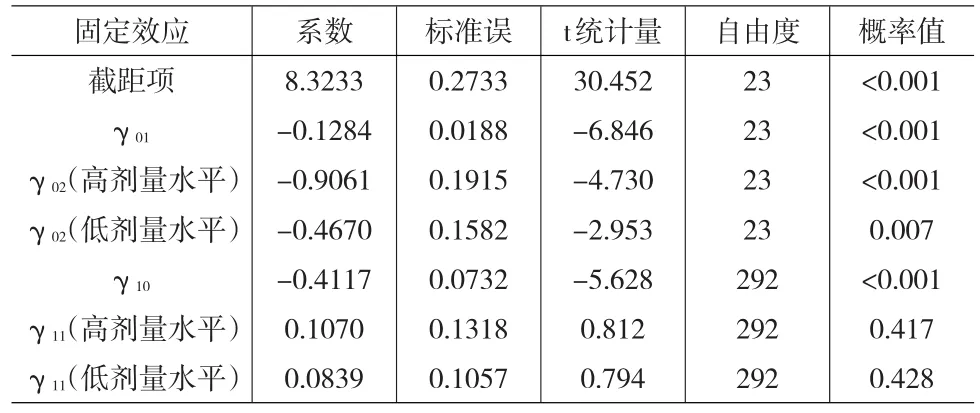
表2　模型各层固定效应的参数估计结果（基于HLM）

表3给出了随机效应方差成分的估计结果和检验结果，表明了该模型的第一层和第二层模型的随机变异情况。表示幼鼠出生体重总变异的37.1%是由第二层的影响因子，即产崽数（litsize）和实验剂量水平（treat）引起的。

表3　随机效应方差成分的估计结果

2.2.3基于R软件（3.13版本）的实现

将上述HLM2转化为等价的混合模型，在此视角下分别采用线性混合模型中的REML方法、GLMM中的惩罚拟似然（Penalized Quasi-Likelihood，PQL）算法与HGLM中的基于h似然的EQL（extended quasi-likelihood，EQL）算法，对式（12）对应的模型分析，得到估计结果如表4所示。

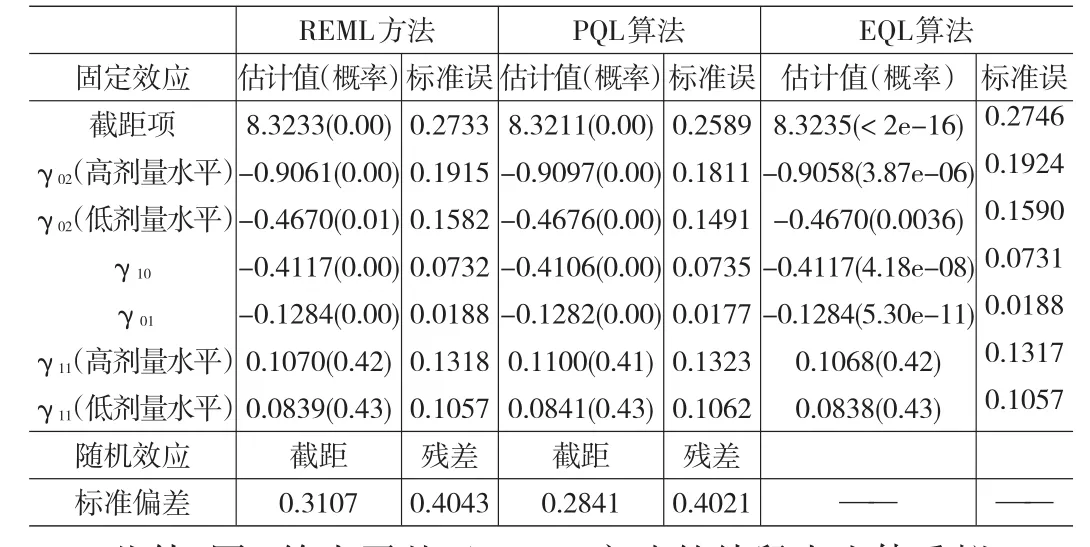
表4　混合模型视角下固定效应和随机效应的参数估计结果（基于R）

此外，图1给出了基于REML方法的幼鼠出生体重拟合值的标准化残差图，可以用于辅助诊断模型的拟合效果。在图1中，大部分标准化残差随机分布在零线上下，且绝对值落在[-2，2]的区间范围内，表明HLM2对应的混合模型的模型假设尚且合理。

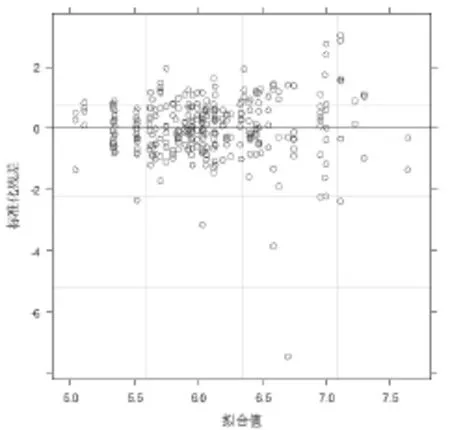
图1　幼鼠出生体重拟合值的标准化残差图

2.2.4结果比较分析

对比表2和表4的输出结果，可以发现：首先，HLM与R软件对模型中固定效应参数估计值、标准误（SE）的估计结果基本相同，t检验结果的统计显著性大致相同。其次，HLM软件可以给出HLM2的标准偏差、方差成分的估计值和σ2=0.0965，见表3），而R软件不能直接给出相应的结果，需要进一步进行计算。其中，随机效应的标准偏差为0.31072=0.0965、方差成分的估计值为σ2=0.40432=0.1635。再次，从LMM视角分析分层数据，基于不同算法进行估计的结果更方便比较；最后，关于反映和衡量模型总体拟合程度的统计指标，HLM2结果中偏差统计量（Deviance）的近似值是399.3，而由于算法不同，R结果中基于REML方法给出AIC统计量的值为419.1043，而基于PQL算法和EQL算法的结果尚未给出AIC统计量的值。

3　分层模型在非寿险精算中的应用与启示

3.1分层模型在非寿险精算中的已有应用研究

国外精算理论界虽然对分层模型在非寿险精算领域的应用已有研究，但尚有深入研究的空间。Jewell(1975)[8]较早地提出分层信度（hierarchical credibility）的概念，由于在处理分层信度模型时，希尔伯特空间技术（Hilbert space technique）通过使用更直观的投影算子取代了繁琐的计算而更胜一筹。Nelder和Verrall(1997)[9]首次将GLM拓展到HGLM，构建分层对数似然函数（hierarchical log-likelihood）并应用于传统的信度理论分析。同时，Nelder和Verrall(1997)在其研究中还提出将HGLM应用于准备金评估和费率厘定的想法和思路。Bühlmann和Gisler(2005)[10]在阐明了实践中很多保险数据具有分层结构的同时，将分层模型理论嵌入到信度模型中，并着重利用该数学方法深入分析分层信度模型。Guszcza (2008)[11]介绍分层模型的概念及其在索赔准备金评估中的应用，并提出对损失流量三角形进行建模的一种新的统计方法，即非线性分层模型（nonlinear hierarchical models），也称为非线性混合模型（nonlinear mixed effects models，NLME）。Frees和Valdez(2008)[12]针对非寿险定价中索赔损失数据，以新加坡财险公司协会（General Insurance Association，GIA）中1993年至2003年的一组汽车保险数据为样本，将其看作具有三层结构的数据集提出了更一般的分层模型，为确定损失数据的联合概率分布，依次分析索赔频率、条件索赔类型与条件索赔强度数据，并应用贝叶斯方法，最终预测未来的总索赔损失。除了分析有层次性和相关性的保险数据之外，HGLM提供一种新的方式，来处理“大规模分类”问题，即如果某个分类变量的水平数较多，而对应于某个水平的数据量较少，那么可以应用HGLM来处理。Ohlsson(2008)[13]把GLM和信度理论结合起来，使用瑞典某保险公司的车险数据，对车型（car model）这一分类变量细分为2500个水平，进行分层信度估计。这方面的文献还有Klinker(2011)。这些研究对于将分层模型应用于非寿险精算实践环节具有较强的借鉴与启发意义。

3.2对中国非寿险业的启示与思考

分层模型的研究方法在社会科学、生物统计等多个领域已得到认可和广泛运用，而越来越复杂的保险大数据启示精算师将其引入并推广到我国的非寿险业。

从宏观角度考察，每一份保单嵌套于保险公司，保险公司嵌套于各省市，各省市嵌套于各个国家，把这些保险数据汇集在一起，将变量进行细化，即可用分层模型做二层、三层、四层甚至更多层次的数据分析。从微观角度思考，对于同一个公司的保险数据，在发生索赔的条件下，索赔的损失分布可以根据索赔频率和索赔额等细分出更多的层次来，费率厘定要考虑每一层次的各种影响因素，每一个因素又可以划分出不同的水平。索赔是否发生、索赔频率、条件索赔类型和条件索赔强度是更一般的分层数据结构。可以引入相应的变量利用HLM统计技术在各个层次内进行费率厘定的建模分析。在影响因素中，各保险公司影响索赔频率和索赔额的数据可以细致划分为人的因素（如驾驶人的年龄、性别、驾驶年龄、职业、是否固定驾驶人员、驾驶人的违章肇事记录、影响驾驶人的安全驾驶因素和驾驶行为等）、车的因素（如车辆年平均行驶里程数、车辆的理赔记录、车辆的使用性质、车型、厂牌型号、核定载客人数、车身颜色、制造年月、事故记录等）、路的因素（如干燥路面、潮湿路面、雪路、冰地、高速公路线形设计、道路结构状况等）和环境因素（如噪音、气象因素等自然环境、地理环境、气候环境、交通环境）等，这一思路见图2。更进一步地，类似于幼鼠实验中其出生体重与不同窝相关的情况，在车险费率厘定中，不同地区驾驶员的索赔可能受到自身风险状况和地区差异的影响，建立类似的分层数据，可以更准确地分析驾驶员的索赔情况。

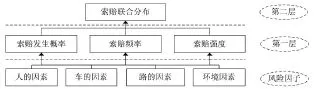
图2　索赔联合分布的分层描述

[1]张晓峒.应用数量经济学[M].北京：机械工业出版社，2009.

[2]lta Kreft,Jan De Leeuw.多层次分析模型导论[M].邱皓政译.重庆：重庆大学出版社，2007.

[3]West B T,Welch K B,Galecki A T.Linear Mixed Models:A Practical Guide Using Statistical Software[M].Boca Raton,FL:Taylor and fran⁃cis/CRC Press,2015.

[4]Lindley D V,Smith A F M.Bayes Estimates for the Linear Model[J]. Journal of the Royal Statistical Society B,1972,(34).

[5]Lee Y,Nelder J.Hierarchical Generalized Linear Models[J].Journal of the Royal Statistical Society B,1996,(58).

[6]Raudenbush S W,Bryk A S.Hierarchical Linear Models:Applica⁃tions and Data Analysis Methods[M].London:Sage Publications,Inc. 2002.

[7]Raudenbush S W,Bryk A S,Cheong Y F,et al.HLM6:Hierarchical Linear and Nonlinear Modeling[M].SSI:Scientific Software Interna⁃tional,Inc.2004.

[8]Jewell W S.The Use of Collateral Data in Credibility Theory:A Hier⁃archical Model[J].Giornale Dell’Instituto Italiano Degli Attuari,1975, (38).

[9]Nelder J A,Verrall R J.Credibility Theory and Generalized Linear Models[J].Astin Bulletin,1997,27(1).

[10]Bühlmann H,Gisler A.A Course in Credibility Theory and Its Appli⁃cations[M].Heidelberg:Springer-Verlag,2005.

[11]Guszcza J.Hierarchical Growth Curve Models for Loss Reserving[J]. Casualty Actuarial Society E-Forum,2008.

[12]Frees E W,Valdez E A.Hierarchical Insurance Claims Modeling[J]. Journal of the American Statistical Association,2008,103(484).

[13]Ohlsson E.Combining Generalized Linear Models and Credibility Models in Practice[J].Scandinavian Actuarial Journal,2008,(4).

（责任编辑/易永生）

O212

A

1002-6487（2016）22-0004-05

国家自然科学基金资助项目（71603180；71271121；71401041）

孙维伟（1982—），女，辽宁海城人，博士，讲师，研究方向：风险管理、统计精算。张连增（1968—），男，山东莱芜人，教授，博士生导师，研究方向：风险管理、统计精算。