基于ARIMA模型的中国民航客运量预测

黄若冰

华南师范大学数学科学学院

基于ARIMA模型的中国民航客运量预测

黄若冰

华南师范大学数学科学学院

本文针对我国民用航空公司客运量问题，依据现有的条件，查找和收集相关数据资料，总和时间序列分析和统计学等知识，采用ARIMA模型，对民航客运量进行分析和预测。

民航客运量；时间序列

1.前言

随着社会的进步，人民生活水平的提高，越来越多的人们选择航空这个交通方式，为合理安排班机数量，估计每年我国民航客运量显得非常有必要。本文在国家数据网站中获得2005年至2014年民航客运量当期值的月度数据，并预测2015至2017年的客运量。

2.建立的模型

2.1模型的分析

ARIMA模型全称为自回归移动平均模型，其中ARIMA(p, d, q)称为差分自回归移动平均模型，AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。ARIMA(p, d, q)称为自回归移动平均模型，有三种基本类型：自回归(AR)模型、移动平均(MA)模型、自回归移动平均(ARMA)模型。

1)AR(p)模型：p阶自回归模型，满足下面的方程：

2)MA(q)模型：q阶的移动平均模型，满足下面的方程：

3)ARMA(p，q)模型将纯AR(p)和MA(q)结合，到一个一般的自回归移动平均方程，得到一个一般的自回归移动平均方程ARMA(p，q)：

2.2模型的建立过程与步骤

2.2.1数据的预处理

首先获取数据时间序列，并在SAS中建立数据集A，作出序列图。发现图形微微呈指数函数上升形式，故做对数变换，生成一个新的数据集lair，并作出序列图，可以发现，该序列有一定的季节性，但在拟合季节性模型之前要先做单位根检验。

2.2.2判断序列的平稳性

通过SAS做单位根检验，输出结果如下：观察DF单位根检验的输出结果，其中“Trend”检验方法的P值小于0.01(本文中假设置信度为ɑ=0.01)，说明不存在单位根，做对数变换之后的序列是一个平稳序列。

2.2.3模型的初步识别

在检验序列的平稳性之后，采用identify过程对模型进行初步的识别。观察输出结果：发现自相关系数保持很大并且彼此很接近，有缓慢下降的趋势。观察偏相关系数，发现其在1步，13步和15步相对较大。因此做一步一阶的差分，得到的自相关与偏相关如下：观察样本自相关系数和偏相关系数，发现样本自相关系数在12步，24步和36步比较大，而偏相关系数在12步比较大。再做12步的一阶差分，发现自相关系数在1步和12步都比较大，故初步把模型定为乘积MA(1)模型：

2.2.4参数估计

用estimate过程对MA(1)模型进行参数的估计观察结果，该模型在0.01的置信水平下通过白噪声检验：

2.2.5异方差检验

采用SAS软件中的reg过程进行异方差检验，可以看到，Reg过程的输出结果显示P值为0.0751，小于0.01，故接受原假设(H0：模型中每一个参数的方差相等)：认为不存在异方差，序列通过异方差检验。

2.2.6模型的确定

由于上述过程中的到的MA(1)模型均通过了参数检验，白噪声检验以及异方差检验，因此将最终模型确定为：

3.利用模型进行预测

使用SAS中的forecast语句，利用上面确定的模型进行预测，并对预测值进行指数变换，同时绘制预测和置信线散点图：(见图1)

上图的绿线表示的是利用模型作出的预测值，红点是本文所用数据真实值，上下两条蓝线之间的区域是置信区间。由此可以看到，虽然预测值与真实值之间仍有写差距，但真实值仍然落在99%的预测区间内，说明拟合效果较好。

长期而言，我国民航客运量整体呈稳步上升趋势，这从一定程度上反映了我国交通运输的发展状况。短期而言，客运量仍处于波动状态，这与具体的短期政策、经济形势有关。

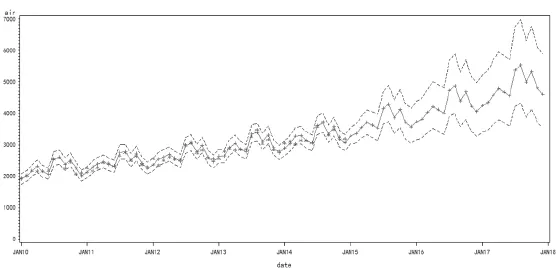
图1

黄若冰(1995-)，男，汉族，华南师范大学数学科学学院金融数学专业。