一种新型非线性时变模型：模糊变参数系统

张洪杨， 梁悦， 班晓军， 吴奋

(1.哈尔滨工业大学 控制理论与制导技术研究中心，黑龙江 哈尔滨 150001；2.北卡罗莱纳州立大学 机械与宇航工程系，美国 罗利 27695-7910)



一种新型非线性时变模型：模糊变参数系统

张洪杨1， 梁悦1， 班晓军1， 吴奋2

(1.哈尔滨工业大学 控制理论与制导技术研究中心，黑龙江 哈尔滨 150001；2.北卡罗莱纳州立大学 机械与宇航工程系，美国 罗利 27695-7910)

为了研究非线性时变模型，提出了模糊变参数系统。它是一种集T-S模糊系统和线性变参数系统诸多优点为一体的新型非线性时变模型，它继承了T-S模糊模型能有效处理非线性系统的优点，又保持了线性变参数模型处理时变系统的优势。模糊变参数系统不仅克服了传统T-S模糊模型在处理时变系统时模糊规则剧增的弱点，也扩展了线性变参数系统理论的适用范围，为解决非线性时变系统的控制问题提供了新思路。在以上模型的基础上，给出了零平衡点全局渐进稳定的一个充分条件以及设计一种T-S全状态反馈控制律的充分条件，数值仿真验证了结果的有效性。

T-S模糊系统；线性变参数系统；模糊变参数系统；二次李亚普诺夫稳定；非线性时变系统

0 引 言

非线性时变系统是控制理论的一个重要研究领域。实际工程中尤其是国防领域中出现的新装备、新系统更是迫使控制理论工作者展开非线性时变系统方面的研究。例如，在飞行器控制领域，考虑到燃料的消耗和气动参数的变化，严格上讲所有的飞行器都是非线性时变系统。而且，这种时变特性会随着飞行器速度、航程、飞行空域的增加而尤显突出。

由于T-S模糊系统具有相对简洁明了的结构以及在一定条件下具有万能逼近器的特性，至今，T-S模糊控制问题仍然是非线性控制领域国内外研究热点之一[1-5]。基于该系统的解析结构分析[6]，模型逼近性能[7]，稳定性分析[8-10]及控制律综合[11-15]，鲁棒性能分析以及鲁棒控制律综合[16]，滤波器设计[18]，增益调度控制[18-20]等问题都得到了广泛研究。这些丰富的研究成果强有力地推动了T-S模糊控制理论的发展与应用。然而，到目前为止，大部分研究主要基于参数恒定的T-S模糊系统，即构成非线性模型的局部线性系统的系统矩阵均为常数矩阵。这种常规的T-S系统具有很好的处理非线性特性的能力，但是在处理时变特性的时候却有局限性，这主要体现在以下两个方面：

1)规则数目剧增，不利于系统分析与综合

为了处理时变特性，需要将与时间有关的参数作为条件变量引入到模糊规则中，这势必会增加模糊规则数。按照经典的并行补偿设计方法，描述被控对象的规则数增加则相应的T-S模糊控制律的规则数目也增加。那么相应的闭环系统的规则数目会倍增。而现有的T-S模糊系统的稳定性分析和综合方法一般都归结到求解一组线性矩阵不等式(linear matrix inequality，LMI)，那么规则数的增加将会直接导致线性矩阵不等式数目的急剧增加，大幅度增加计算量，进而提高控制系统分析与综合的计算复杂度。

2)对时变特性的“近似”描述

正如一般情况下T-S模糊模型是对非线性系统的一种近似描述，一旦把时变参数作为模糊变量引入到条件变量中，一般情况下也是对系统时变特性的一种近似描述，这无疑会引入模型误差，也会给系统分析与控制律综合带来更多保守性。

综上所述，尽管T-S模糊系统能有效处理非线性被控对象，但在处理被控对象的时变特性方面具有局限性。

而另一方面，上个世纪90年代以来，基于线性变参数系统(linear parameter varying systems，LPV)的理论[21-22]得到了长足发展。该理论主要是解决以下线性时变系统的分析与综合问题：

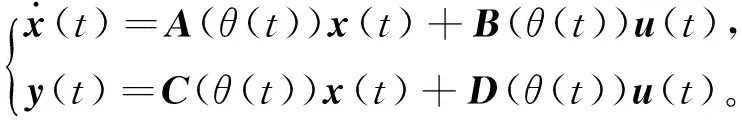
其中θ(t)∈Rm是随时间变化的独立于系统状态变量的参数。借助于凸优化理论，各种基于线性变参数系统的问题都得到了很广泛的研究。例如稳定性分析、镇定问题、保证输出输入性能的控制律综合问题等，其理论框架基本成熟。一般情况下，这些问题最后都归结到求解一组依赖参数θ(t)的线性矩阵不等式。目前，该理论已将线性定常控制理论发展到了线性时变控制理论，能有效处理线性时变系统的控制系统分析与综合问题。但该理论构建在线性时变模型的基础上，其处理非线性对象的能力有限。仅管在一定条件下可以将非线性模型转化为一种“伪线性变参数模型”的形式，但会带来分析设计上的保守性。所以从理论上讲，我们需要将现有的线性变参数理论推广到非线性领域。

基于以上考虑，本文提出了一种新型的非线性时变模型，称之为模糊变参数系统(fuzzy parameter varying systems，FPV)。该系统能够克服一般T-S模糊模型在描述时变特性时存在的局限性，结合T-S模糊系统和线性变参数系统的特点于一身，直接面向非线性时变系统，将为解决非线性时变系统的控制问题提供一种新的理论途径。

1 模糊变参数系统

假设模糊变参数系统规则库中共有r条规则，则第i条规则形式如下：

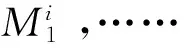
(1)

其中：

将式(1)所描述的系统称为模糊变参数系统。

可以看出，系统(1)中的Ai(·)，Bi(·)，Ci(·)和Di(·)不依赖时变参数θ(t)的时候，该系统即退化为一个普通的T-S系统，体现出描述非线性被控对象的能力；当规则库中只有一条规则或者每条规则对应的线性模型的参数都相同时，该系统又退化为一个普通的线性变参数系统，体现出处理时变特性的能力。因此，该系统是集T-S模糊系统和线性时变参数系统特点于一身，是一种描述非线性时变系统的数学模型。

值得注意的是，从理论上讲，T-S系统的条件变量z(t)完全可以是与系统状态或者输出无关的随时间变化的量，从而整个T-S模型可以体现出时变特性。但正如绪论以及第三节中所描述，用这种方式描述时变系统具有很大的局限性。所以只假设式(1)中的条件变量z(t)仅仅是状态变量或输出变量。

注：现阶段的T-S模糊模型大多数是集中参数系统，但是在实际生产和过程中，状态变量不仅与时间有关还会与空间变量相关，例如流体问题、化学反应过程等。因此状态变量严格意义上也是空间变量的函数。从而可以得到偏微分模糊系统。从偏微分模型角度考虑，偏微分模糊变参数系统有r条规则组成，其中第i条规则具有如下形式：

(2)

2 T-S模糊模型与FPV模型的对比

T-S模糊模型在描述非线性时变系统的时候具有局限性。这是因为通常要将时变参数当作一个新的条件变量加入到模糊规则中。以下面用倒立摆的数学模型来说明这一点。一级倒立摆的数学模型为：

规则1：如果x1在0弧度附近，那么

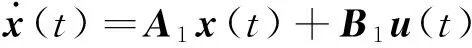
规则2：如果x1在0.489π弧度附近，那么

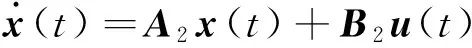
假设以上非线性模型中的摆杆长度是时间的函数，即l=1.5+cos(t)。如果还用传统T-S模糊模型建模，可以把摆杆长度当成一个条件变量来处理。在最简单的情况下，可以得到4条模糊规则的T-S模糊模型：

规则1：如果x1在0弧度附近并且l在1.75 m附近，那么

规则2：如果x1在0弧度附近并且l在2.25 m附近，那么

规则3：如果x1在0.489π弧度附近并且l在1.75 m附近，那么

规则4：如果x1在0.489弧度附近并且l在2.25 m附近，那么

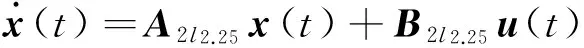
其中：

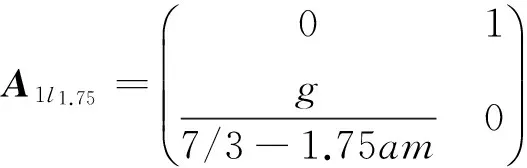
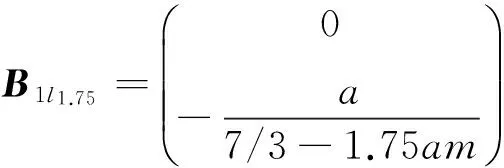
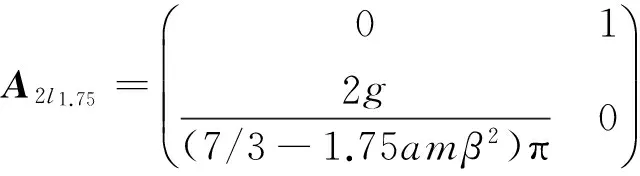
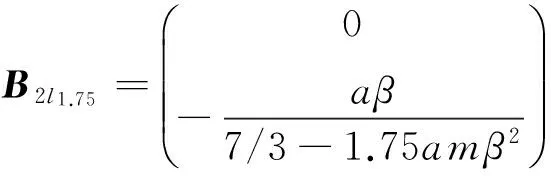
可以看出T-S模糊模型在描述时变系统的时候，模糊规则从2条变成了4条。这还仅仅是最简单的情况，倘若希望进一步提高模型精度，需要对摆杆长度进行更细致的模糊划分，势必会得到更多的模糊规则，这将为后续的控制器设计和综合问题带来很大困难。

针对更为一般的非线性时变系统，应用常规T-S系统近似系统时，可行的做法是将所有不属于状态变量的其他随时间变化的参数θ(t)视为条件变量，即将这些变量包含在z(t)中。此时，该系统可以描述时变非线性系统。但这种做法会将直接导致规则数目呈指数形式增长。假设z(t)中原有n个变量，对每个变量进行s个模糊划分，则不对规则进行化简时，完备的规则库中会包含sn条规则。考虑新增加的时变参数，若对于时间参数θi(t)，i=1,2,…,m所在论域也进行s个模糊划分，则不做任何规则简化时，规则数目会增加到s(m+n)。以此计算，整体会增加sn(sm-1)条规则。假设z(t)中原有2个变量，即n=2，并对每个参数所在论域进行7个模糊划分(这是一种很通常的做法：负大、负中、负小、零、正小、正中、正大)，即s=7。此时，规则数目会增加72×(72-1)=2 352条。该数字会随着变量个数的增加呈指数形式增长，而FPV系统恰好能克服T-S系统这个弱点。

3 模糊变参数系统稳定性分析

稳定性分析是控制系统研究中的一项重要工作。基于二次型Lyapunov函数，我们可以得到保证系统零平衡点全局渐进稳定的一个充分条件。考虑如下不带控制量的模糊变参数系统

(3)

式中x是状态变量，Ai(θ)∈Rn×n是系统矩阵，其它参数与式(1)中相同。

选取如下二次Lyapunov函数

V(x)=xTPx，

其中P∈Rn×n是一个正定的常数矩阵。计算V(x)沿着系统(3)的导数为

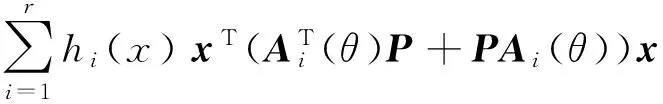
据此，可以得到下面稳定性充分条件。

定理1：如果存在正定矩阵P并且对于任意的θ∈Ω满足下面矩阵不等式

那么系统(3)的原点是全局渐近稳定的。

进一步，考虑以下闭环系统：

(4)

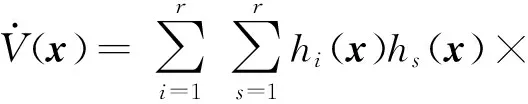
[(Ai(θ)+BiKs)TP+P(Ai(θ)+BiKs)]<0,

可以知道系统(4)的原点是全局渐近稳定的条件：

存在矩阵正定矩阵P和矩阵Ks满足

(Ai(θ)+ Bi(θ)Ks)TP+P(Ai(θ)+

Bi(θ)Ks)<0,

(5)

其中i,s=1,2,…,r。将式(5)分别左乘和右乘P-1，可以得到

(6)

可以看出上面的式子可以解出P和Ks。据此可得以下控制器综合条件。

定理2：如果存在正定矩阵P和矩阵Qs并且对于任意的θ∈Ω满足下面线性矩阵不等式

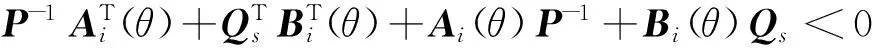
其中，i=1,2,…,r，s=1,2,…,r，然后取控制器

Ks=QsP，s=1,2,…,r。

则闭环系统(4)的原点是全局渐近稳定的。

注：如果Ω是凸多边形，式(6)为有限个线性矩阵不等式。

4 数值仿真

以下我们将通过数值仿真验证上述方法设计控制器的有效性。为了简化起见，取n=2，r=2，Ai(θ)=Ai0+Ai1θ1。针对于如下变参数模型以及全状态反馈控制器：

(7)

首先写出关于式(6)的线性矩阵不等式组：

可以通过Matlab中的LMI工具箱可以解出：

然后将K1和K2代入系统(7)中，使用Matlab中的SIMULINK工具进行数值仿真，得到系统状态图2和图3。

图1 θ1(t)的图像Fig.1 Curve of θ1(t)

图2 初值为(1,-1)系统(7)的状态Fig.2 State of system(7)with initial (1,-1)

图3 初值为(20,-200)系统(7)的状态Fig.3 State of system(7)with initial (20,-200)

从图2可以看出当初值是(1,-1)时，状态变量x1和x2都会收敛到0。在图3中，初值选取为(20,-200)，也可以看到状态变量收敛到0。

注：由于本算例没有实际物理意义，所以图1～图3的纵坐标没有单位。

5 结 论

本文提出了一种新型非线性时变模型：模糊变参数系统。该系统为解决非线性时变系统的控制问题提供了新思路，它是经典T-S模糊模型以及LPV系统的推广和延伸。进一步，我们给出了零平衡点全局渐进稳定的一个充分条件以及设计T-S全状态反馈控制律的充分条件。数值仿真验证了以上结果的有效性。

[1] ZHAO Xudong, YIN Yunfei, ZHAN Lixian G, et al. Lpcontrol of switched nonlinear systems via T-S fuzzy modeling[J].IEEE Transaction on Fuzzy Systems,2016,24(1):235-241.

[2] ZHANG Yanjun, TAO Gang, CHEN Mou. Relative degrees and adaptive feedback linearization control of T-S fuzzy systems[J].IEEE Transaction on Fuzzy Systems,2015,23(6):2215-2230.

[3] CHEN Jun, XU Shengyuan, ZHANG Baoyong, et al. Novel stability conditions for discrete-time T-S fuzzy systems: a kronecker-product approach[J].Information Sciences,2016,337-338:72-81.

[4] FENG Gang. Analysis and synthesis of fuzzy control systems: a model-based approach[M].London:Taylor and Francis Group,2010.

[5] LI Hongyi, LIU Honghai, GAO Huijun, et al. Reliable fuzzy control for active suspension systems with actuator delay and fault[J].IEEE Transactions on Fuzzy Systems,2012,20(2):342-357.

[6] DING Yongshen, YING Hao, SHAO Shihua.Typical Takagi-Sugeno PI and PD fuzzy controllers: analytical structures and stability analysis[J].Information Science,2003,151:245-262.

[7] YING Hao, DING Yongsheng, LI Shakuan, et al. Comparison of necessary conditions for typical takagi-sugeni and mamdani fuzzy systems as universal approximators[J].IEEE Transaction on Fuzzy Systems, Man and Cybernetics, Part A,1999,29(5):508-514.

[8] TANAKA K, HORI T,WANG H. A multiple lyapunov function approach to stabilization of fuzzy control systems[J].IEEE Transactions on Fuzzy System,2003,11(4):582-589.

[9] ZHANG Huaguang, XIE Xiangpeng. Relaxed stability conditions for continuous-time t-s fuzzy-control systems via augmented multi-indexed matrix approach[J].IEEE Transaction on Fuzzy Systems,2011,19(2):478-492.

[10] TANIGUCHI T, TANAKA K, WANG H. Fuzzy descriptor systems and nonlinear model following control[J].IEEE Transactions on Fuzzy System,2000,8(4):442-452,

[11] XIU Zhihong, REN Guang. Stability analysis and systematic design of Takagi-Sugeno fuzzy control systems[J].Fuzzy Sets and Systems,2005,151(1):119-138.

[12] CHEN Yingjen, OHTAKE H, TANAKA K, et al. Relaxed stabilization criterion for t-s fuzzy systems by minimum-type piecewise-lyapunov-function-based switch fuzzy controller[J].IEEE Transaction on Fuzzy Systems,2012,20(6):1166-1173.

[13] DONG Jiuxiang, YANG Guanghong. Control synthesis of T-S fuzzy systems based on a new control scheme[J].IEEE Transaction on Fuzzy Systems,2011,19(2):323-338.

[14] DING Baocang. Homogeneous polynomially nonquadratic stabilization of discrete-time takagi-sugeno systems via nonparalled distributed compensation law[J].IEEE Transaction on Fuzzy Systems,2010,18(5):994-1000.

[15] LIU Huangping, SUN Fuchun, HU Yenan. H∞control for fuzzy singularly perturbed system[J].Fuzzy Sets and Systems,2005,155(2):272-291.

[16] HUANG Jin, CHEN Yehua，CHENG A. Robust Control for fuzzy dynamical systems: uniform ultimate boundedness and optimality[J].IEEE Transaction on Fuzzy Systems, 2012,20(6):1022-1031．

[17] ZHANG Zhuo, ZHANG Zexu, ZHANG Hui, et al. Finite-time H1filtering for t-s fuzzy discrete-time systems with time-varying delay and norm-bounded uncertainties[J].IEEE Transactions on Fuzzy Systems,2015,23(6):2427-2434.

[18] XIE Wei. Improved L2gain performance controller synthesis for Takagi-Sugeno fuzzy system[J].IEEE Transaction on Fuzzy Systems,2008,16(5):1142-1150.

[19] SOUZA C, OSOWDKY J. Gain-scheduled control of two-dimensional discrete-time linear parameter-varying systems in the Roesser Model[J].Automatica,2013,49(1):101-110.

[20] LIU Yang, BAN Xiaojun, WU Fen, et al. A gain-scheduling control approach for t-s fuzzy systems based on linear parameter-varying control theory[J].ASME Journal of Dynamic Systems, Measurement,and Control,2016,138(1):0110081-0110089.

[21] WU Fen. A generalized lpv system analysis and control synthesis framework[J].International Journal of Control,2001,74(7):745-759.

[22] WU Fen, DONG Ke. Gain-scheduling control of lft systems using parameter-dependent lyapunov function[J].Automatica,2006,42:39-50.

[23] TANAKA K,WANG H. Fuzzy control system design and analysis—a linear matrix inequality approach[M].Hoboken:John Wiley & Sons Inc,2001：20-58.

(编辑：刘琳琳)

Nonlinear time-varying model: fuzzy parameter varying system

ZHANG Hong-yang1, LIANG Yue1, BAN Xiao-jun1, WU Fen2

(1.Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China; 2. Mechanical and Aerospace Engineering Department, North Carolina State University, Raleigh 27695-7910, USA)

The fuzzy parameter varying system was proposed to study nonlinear time-varying models. It is a novel nonlinear model combining the advantages of both the T-S fuzzy system and the linear parameter varying (LPV) system. It inherits the advantage of the T-S fuzzy system in dealing with nonlinear systems effectively, and maintains the advantage of LPV system when processing linear time-varying systems. Fuzzy parameter varying system not only overcomes the disadvantage of the traditional T-S fuzzy system in handing time-varying systems, but also expands the scope of application of LPV system theory. It provides a new idea for solving nonlinear time-varying control problem. Moreover, a sufficient condition is provided to guarantee the globally asymptotically stable of the equilibrium and to synthesize a T-S state feedback control law which can stabilize the closed loop fuzzy parameter varying system. Numerical simulations verify the effectiveness of our results.

T-S fuzzy system; linear parameter varying system; fuzzy parameter varying system; quadric Lyapunov stability; nonlinear time-varying system

2016-07-22

国家自然科学基金(61304006，61273095)

张洪杨(1987—)，男，博士研究生，研究方向为模糊变参数系统理论与应用；

梁 悦(1994—)，女，硕士研究生，研究方向为模糊变参数系统理论与应用；

班晓军

10.15938/j.emc.2016.11.012

TP 273

A

1007-449X(2016)11-0086-06

班晓军(1978—)，男，博士，教授，博士生导师，研究方向为模糊系统、鲁棒增益调度控制；

吴 奋(1964—)，男，博士，教授，研究方向为鲁棒增益调度控制。