盘式永磁涡流驱动器的涡流软测量方法

时统宇， 王大志， 石松宁， 郑迪， 李召

(东北大学 信息科学与工程学院，辽宁 沈阳 110819 )



盘式永磁涡流驱动器的涡流软测量方法

时统宇， 王大志， 石松宁， 郑迪， 李召

(东北大学 信息科学与工程学院，辽宁 沈阳 110819 )

针对永磁涡流驱动器导体盘在工作状态时无法直接测量涡流的问题，提出一种涡流软测量的方法。建立永磁涡流驱动器的解析计算二维模型，引入矢量磁位构建偏微分方程组，借助各层的边界条件，得到了导体铜盘涡流的解析解，从而得到导体铜盘上的涡流分布规律。采用该模型，永磁涡流驱动器在运行过程中所产生的涡流密度可以通过转差速度和气隙宽度的测量结果计算得到。之后应用涡流软测量模型，分析导体盘涡流密度大小随气隙宽度和转差速度变化的变化规律。所有计算得到的软测量结果都进行了基于有限元法的仿真验证。结果表明，涡流解析计算有较好的准确性，该软测量模型的结果平均误差约为2%，为永磁涡流驱动器运行过程中涡流的计算和产品优化设计提供了重要依据。

盘式永磁涡流驱动器；涡流软测量；解析分析；有限元法

0 引 言

永磁涡流驱动器作为最近发展很快的调速设备，逐渐广泛应用在风机水泵等设备上，其采用无接触的机械结构传递能量，在电机转速不变的情况下，通过调节铜盘和磁盘之间的气隙来改变电机与负载之间的转速差，来调节永磁涡流驱动器的输出转速，实现速度控制。通过该装置应用，最大优点是不会如变频器调速那样产生对电网的谐波污染，也不用进行轴的精确校准[1-4]。

永磁涡流驱动器作为一种基于涡电流作用而工作的设备中的典型代表，对其产生涡流情况的检测和分析是十分重要的。永磁涡流驱动器的涡流存在着两方面的意义，一方面扭矩的传递需要铜盘中的涡流产生磁场与永磁体进行耦合，进而产生转矩；另一方面永磁涡流驱动器的功率损耗主要以涡流产生热量的形式从导体铜盘上释放出来，这降低了永磁涡流驱动器的传动效率。同时，永磁体工作性能会受到其居里温度的限制，在接近或者超过其居里温度时，永磁体的磁性会受到很大影响，甚至会发生永久失磁的现象，这对于永磁涡流驱动器是非常严重的问题[5]。

当永磁涡流驱动器处于工作状态时,要对导体盘上的涡流进行直接测量是十分困难的，传统的测量导体涡流的方法是在被测部分上打很细的孔,把探针准确地埋设在预定的孔内,测量两点之间的电位差，然后根据导体的电导率和测点间的距离计算得出平均涡流[6]。由于复杂性和欠精确性等原因，这种方法逐渐显现弊端。

永磁涡流驱动器分为盘式和筒式两种，盘式永磁涡流驱动器以其结构简单等特点成为各国学者研究的重点。近些年，各国学者对永磁涡流驱动器的涡流和涡流损耗进行了建模和分析。众所周知，设备的设计最需要的是关键指标的计算的精确性，可以利用2D或3D的数值方法，对相应的涡流问题进行模拟仿真和计算[7-9]；利用有限元法，一些学者也设计了很多新式结构的永磁传动设备，然而数值方法计算时间长，占用计算机内存更大，方法较为复杂。相比之下，解析算法会在计算速度上得到很大提升[10]。文献[11]利用层理论构建了永磁涡流驱动器的数学模型，用解析法引入矢量磁位对转递扭矩进行了计算，但是未对涡流问题进行详细研究。文献[12]立足于有限元仿真结果，提出了一种基于最小二乘法的高速磁浮列车电磁力的软测量方法，估算精度较高，易于实现，但建模机理性稍有缺陷。

本文提出了一种涡流软测量的方法，预先建立起永磁涡流驱动器的解析计算涡流软测量模型，通过气隙宽度、转差速度等参数的精度测量，引入矢量磁位构建微分方程组，解得导体铜盘上的涡流分布规律，来间接评估出永磁涡流驱动器在传动过程中所产生的涡流密度的大小。之后进行了有限元仿真与软测量的结果进行对比，验证了涡流解析计算软测量的准确性，对于初步设计时分析永磁涡流驱动器的涡流问题及其损耗，具有很重要的意义。

1 机械结构与工作原理

1.1 机械结构

盘式永磁涡流驱动器的机械结构示意图如图1所示。驱动器大体上分为两部分：主动转子和被动转子。主动转子是由背钢和铜盘组成，跟随电机轴一起转动，而被动转子是由背钢、铝盘和永磁体三部分组成的。主动转子和被动转子之间存在气隙，涡流驱动器装有气隙调节装置，用于调节气隙宽度大小。

图1 永磁涡流驱动器Fig.1 PM eddy-current drivers

1.2 工作原理

永磁涡流驱动器采用柔性传动的方式，它的主、从动转子各自可以自由的独立旋转。当电机带动主动转子旋转时，导体铜盘切割从动转子中永磁体的磁力线后，在表面上产生涡电流，进而形成感应磁场。感应磁场对永磁体共同作用，产生耦合力，带动从动转子与主动转子同方向旋转。耦合力的大小可以通过调节气隙磁通密度大小进行调节，而磁通密度是通过气隙调节装置进行控制的。气隙调节装置可以进行手动和电动调节，控制与其相连的步进电机转速和方向就可以实现闭环的自动控制。

永磁涡流驱动器的这种工作方式有以下优势：

1)利用全新柔性传动的机械方式实现了电动机的扭矩传递和负载速度调节，具有隔振护轴、过载保护、轻载启动等作用。

2)与目前主流电动机调速设备——变频器相比，永磁涡流驱动器采用了纯机械非接触性式结构，有效地消除了电力谐波污染、电磁干扰、避免电机与负载间振动的传递，真正实现了绿色节能。

3)调节扭矩和转速时，仅通过调节轴向气隙间距即可完成，原理简单，可靠性强。

2 永磁涡流驱动器的软测量模型分析

软测量技术也称为软仪表技术，基本原理为: 利用那些与难于检测的主导变量有密切关系的易测变量，通过建立数学关系模型，得到难检测变量的预估值。软测量技术常用的方法包括机理建模分析、非线性回归分析、神经网络等。采用基于线性理论的机理推导，是在建立软测量涡流模型的情况下，根据可测变量，通过程序运算，得到涡流密度的估计值。

2.1 永磁涡流驱动器模型假设

考虑到永磁涡流驱动器结构的复杂性与对称性，鉴于三维解析模型过于复杂并且重要参数亦存在于二维模型中，根据线性理论，将三维问题化为二维问题处理，进而采用分离变量法建立二维软测量模型。选取永磁体平均半径处的周向截面并展开成平面。

图2是永磁涡流驱动器的简化后得到的2D模型，如图所示，涡流驱动器可以分为4层，其中导体铜盘侧钢盘的厚度为为Li，气隙为g，铜盘的厚度为d，建立极坐标系，对永磁涡流驱动器进行建模。

图2 涡流驱动器的结构模型Fig.2 2D model of a PM eddy-current driver

首先对各区域进行简要说明：

区域Ⅰ：导体环背后的钢盘。

区域Ⅱ：导体铜盘。区域中的涡流取决于导体转子与永磁转子间的转速滑差和气隙宽度。

区域Ⅲ：空气间隙。

区域Ⅳ：永磁体与铝盘。区域中铝盘主要起到固定与隔磁的作用，减少磁体间横向漏磁，使磁通主要集中在轴向气隙，以便产生更大的转矩。

对于以上模型，设定如下的假设：

1)导体盘以及其后的背铁，永磁体、铝盘和其后的背铁都是各自相对静止，而主动部分和从动部分存在着一定的转速差；

2)忽略端部效应；

3)忽略温度对材料性能的影响；

4)永磁体被均匀磁化。

基于以上假设，对于永磁涡流驱动器的涡流进行计算。

2.2 涡流驱动器涡流软测量模型的建立

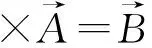
(1)

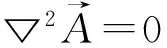
(2)

其中：μ是各区域的磁导率；J是由于主动转子和从动转子之间的滑差在各区域中感应得到的电流密度。

区域Ⅰ：在涡流驱动器导体盘背铁中，

(3)

在主动转子中，感应得到的电流密度可以由公式(4)求得：

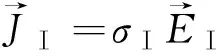
(4)

其中σⅠ是区域Ⅰ的导电率。

根据法拉第电磁感应定律，

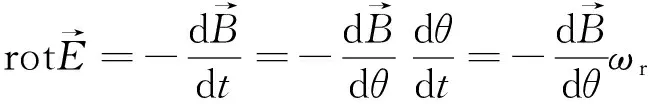
(5)

其中ωr是圆盘的切向角速度。

所以，

(6)

那么区域Ⅰ的磁场方程最终为

(7)

同理，区域Ⅱ的磁场方程为

(8)

区域Ⅲ：由于气隙磁场中没有电流产生，所以得到区域的磁场方程

(9)

(10)

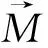
(11)

其中：n为傅里叶级数中的nth谐波；p为极对数；Mzn为傅里叶级数的系数，其计算式为

(12)

其中αp和Br是磁弧长度和磁极距的比和剩余磁感应强度。

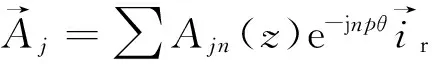
(13)

其中j=Ⅰ,Ⅱ,Ⅲ,Ⅳ。

因为：

(14)

所以式(7-9)可以重写为：

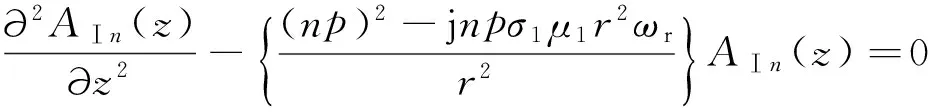
(15)

(16)

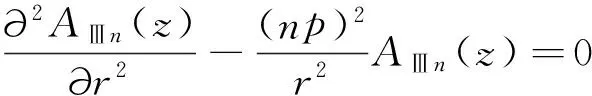
(17)

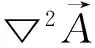
▽2AⅣ-eddy=0,

(18)

▽2AⅣ-pm=0。

(19)

所以得到方程详细表达式为

(20)

利用待定系数法，求解各区域的磁矢势可以得到以下公式：

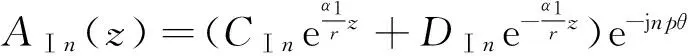
(21)

(22)

(23)

(24)

其中：

(25)

(26)

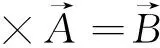
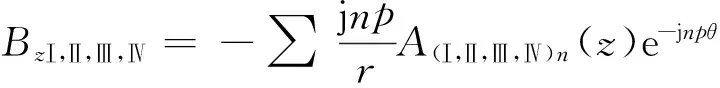
(27)

(28)

各区域的边界条件为：

AⅠ|z=-Li=0,

(29)

BZⅠ|z=0=BZⅡ|z=0and HθⅠ|z=0=HθⅡ|z=0,

(30)

BZⅡ|z=d=BZⅢ|z=dand HθⅡ|z=d=HθⅢ|z=d,

(31)

BZⅢ|z=d+g=BZⅣ|z=d+gand HθⅢ|z=d+g

=HθⅣ|z=d+g,

(32)

AⅣ|z=inf=0。

(33)

根据上述的边界条件可以得到式(34)：

(34)

由公式

(35)

可以得出，导体盘的涡流密度可以由方程中的转差速度和气隙宽度以及其他参数尺寸获得，当模型尺寸固定时，涡流密度仅和速度以及气隙宽度有关，这样就可以得到一个由机理分析得到的软测量模型。

3 基于有限元仿真的算法验证

3.1 永磁涡流驱动器的有限元仿真

应用ANSYS软件[13]建立了涡流驱动器的仿真模型。通过比较软测量模型和仿真结果，验证软测量算法的有效性。主要仿真参数如下：永磁体剩余磁感应强度为1.3 T，导体材料选择铜，厚度10 mm；永磁体宽度30 mm，厚度20 mm，磁极间距10.14 mm；钢盘厚度为10 mm，气隙宽度为3 mm，电机输出转速为1 455 r/min。有限元仿真模型如图3所示。

图3 永磁涡流驱动器的二维有限元仿真模型Fig.3 2D finite element simulation model of PM eddy-current driver

永磁涡流驱动器的涡流密度分布如图4所示。由图可知：涡流主要集中在铜盘表面附近的一薄层中，相邻涡流回路的方向截然相反，相邻回路的涡流密度均在铜盘表面取得最大值，大体呈正弦形状。

图4 二维运动涡流场的涡流密度等值图Fig.4 2D FE eddy current chorisogram of a PM eddy-current driver

3.2 算法验证与分析

图5显示了在转差速度为300 r/min时铜盘表面轴向磁场密度随着角θ变化的趋势。曲线显示，铜盘表面的轴向磁场密度随θ成近似正弦变化趋势，并受到涡流影响略有削顶现象，且与有限元仿真结果一致性较好。

图6显示了在转差速度为300 r/min时，铜盘表面涡流密度随着角θ变化的有限元分析结果和软测量模型求得的涡流密度的计算结果的比较曲线。涡流曲线变化规律和相位与轴向磁场密度相同，经过比较可以得出，图中软测量模型求得的铜盘上的涡流密度计算结果与有限元仿真结果有着很好的吻合。

对比软测量计算模型和有限元分析的结果可以得到如下结论:1)从图5和图6中可以看出，软测量机理模型和有限元法拟合得较好，证明推导的软测量机理解析方法是有效的，正确的；2)从图6可以分析得出，随着角度的增加，导体铜盘表面的涡流密度呈现周期性变化的趋势，与轴向磁场的变化规律吻合，且大小和方向也可以计算分析得出。

图5 铜盘二维轴向磁场密度曲线Fig.5 2D axial magnetic field density curve of the PM eddy-current driver

图6 铜盘涡流密度有限元分析和软测量模型计算结果比较曲线Fig.6 Comparison curve between the soft measurement model and the finite element method

进一步验证软测量方法的准确性，可以设定在其他参数不变的情况下，在可选范围内选取不同气隙和转差速度，比较有限元仿真和软测量模型的涡流密度结果，见表1(角度θ为0°)。从表中可以看出, 利用软测量模型计算得到的涡流密度与有限元法分析结果之间的平均误差约为2%, 最大误差小于4%，因而可为涡流驱动器的工程计算和散热分析提供重要依据。

表1 软测量结果与有限元法结果的对比及误差

4 软测量模型的应用

利用软测量机理模型的准确性强、延伸性高的特点，计算分析了一定角度范围内，不同气隙大小和滑差速度下的径向涡流密度大小的变化曲线，以进一步探究涡流大小的变化规律，分析涡流大小和结构参数之间的关系。

图7表示在300 r/min的滑差速度下，气隙大小分别是3、5、7 mm时，涡流密度大小的变化趋势。

图7 铜盘涡流密度软测量结果随气隙大小变化曲线Fig.7 Curve of current density against air gap using soft measurement model

根据图中曲线对比可以得到，涡流密度大小随角度变化的趋势呈现近似余弦的形状，随着气隙的增加，涡流密度幅值减小，且幅值的减小幅度也越来越小。其原因是，在气隙较小时，轴向磁通密度大小受到气隙大小的变化影响较大，较为敏感。

图8表示了在3 mm气隙下，滑差速度分别是100、300、500 r/min时，涡流密度大小的变化趋势。

图8 铜盘涡流密度软测量结果随滑差速度变化曲线Fig.8 Curve of current density against slip velocity using soft measurement model

根据图中曲线对比可以得到，涡流密度大小随滑差速度变化的趋势也呈现近似余弦的形状，随着速度的增加，涡流密度幅值增加，且震荡幅度越发明显。其原因是，随着滑差速度的增加，由涡流产生的磁场对合成磁场的影响变大，这也是Rogowski解析法的有力证明。

5 结 论

本文介绍了利用机理软测量模型进行涡流分析的方法，该方法应用在永磁涡流驱动器铜盘的涡流问题中，计算得到了其各个位置的涡流密度分布和大小。其结果与有限元仿真得到的结果进行了对比，对比结果表明，解析法与有限元结果有很好的吻合，拥有同样的变化规律，证明此方法在涡流计算中是有意义的。最后利用机理软测量法得到了永磁涡流驱动器涡流密度相对于滑差速度、气隙长度变化所引起的涡流密度变化趋势，为永磁涡流驱动器的设计和研发提供了比较准确的参考。证明机理软测量模型法具有非常好的准确性，为涡流驱动器的前期设计和后期优化，提供了一种行之有效的方法。

[1] A Wallace,A Von Jouanne.Industrial speed control: are PM couplings an alternative to VFDs?[J]. Industry Applications Magazine, IEEE, 2001, 7(5): 57-63.

[2] 王旭, 王大志. 永磁调速器的磁路结构设计[J]. 电气传动, 2011, 41(10): 55.

WANG Xu,WANG Dazhi.Magnetic circuit structural design of permanent magnetic driver[J].Electric Drive,2011,41(10):55.

[3] 杨超君, 管春松, 徐燕飞, 等. 盘式异步磁力联轴器三维气隙磁场计算及试验研究[J]. 电机与控制学报, 2013, 17(1)：51-57.

YANG Chaojun, GUAN Chunsong, XU Yanfei, et al. Theoretical arithmetic and experimental study on 3D air gap magnetic field for axial asynchronous permanent magnet couplings[J]. ElectricMachines & Control, 2013, 17(1)：51-57.

[4] S Mohammadi,M Mirsalim,S Vaez-Zadeh S. Nonlinear modeling of eddy-current couplers[J].IEEE Transactions on Energy Conversion,2014，29(1)：224-231.

[5] A Canova,F Freschi.Multi objective design optimization and Pareto front analysis of a radial eddy current coupler[J]. International Journal of Applied Electromagnetics and Mechanics, 2010, 32(4): 219-236.

[6] 赵小波. 永磁式涡流缓速器电磁特性与制动性能研究[D].南京：南京农业大学, 2009.

[7] Albertz D, Dappen S, Henneberger G. Calculation of the 3D nonlinear eddy current field in moving conductors and its application to braking systems[J].IEEE Transactions on Magnetics,1996, 32(3):768-771.

[8] W Nehl T,B Lequesne,V Gangla,et al.Nonlinear two-dimensional finite element modeling of permanent magnet eddy current couplings and brakes[J].IEEE Transactions on Magnetics, 1994,30(5):3000-3003.

[9] WANG J,LIN H,FANG S,et al.A general analytical model of permanent magnet eddy current couplings[J]. IEEE Transactions on Magnetics,2014,50(1):1-9.

[10] 王旭, 王大志, 刘震, 等. 永磁调速器的涡流场分析与性能计算[J]. 仪器仪表学报, 2012, 33(1): 155-160.

WANG Xu, WANG Dazhi, LIU Zhen, et al.Eddy current field analysis and performance calculations for adjustable permanent magnetic coupler[J].Journal of Scientific Instrument, 2012, 33(1):155-160.

[11] CHOI J Y,JANG S M.Analytical magnetic torque calculations and experimental testing of radial flux permanent magnet-type eddy current brakes[J]. Journal of Applied Physics, 2012, 111(7): 07E712.

[12] 陈棣湘, 潘孟春, 罗飞路. 高速磁浮列车电磁力的软测量技术[J]. 电机与控制学报, 2006, 10(3): 234-237.

CHEN Dixiang, PAN Mengchun, LUO Feilu. Electromagnetic forces' soft measurement technology of high speed magnetic levitation vehicle[J]. Electric Machines & Control, 2006, 10(3):234-237.

[13] 秦伟, 范瑜, 马育华, 等. 盘式永磁Halbach悬浮装置的磁场和力特性分析[J]. 电机与控制学报, 2012, 16(6): 57-62.

QIN Wei,FAN Yu,MA Yuhua, et al.Characteristic and magnetic field analysis of disc Halbach permanent magnets maglev device[J].Electric Machines & Control,2012,16(6):57-62.

(编辑：张 楠)

Eddy current soft measurement method of disk type PM eddy-current driver

SHI Tong-yu， WANG Da-zhi， SHI Song-ning， ZHENG Di， LI Zhao

(School of Information Science & Engineering, Northeastern University, Shenyang 110819, China)

In order to solve the problem of immeasurabilty of eddy current density on the conductor plate, a eddy current soft measurement method was proposed.2D analytical model was established of eddy current problem of eddy-current driver. The eddy current density on conductor plate is calculated by solving differential equations of magnetic vector potential. The undefined coefficients in equations are determined by applying boundary conditions. Eddy current density of the PM eddy-current driver during run time was calculated by measured data of slip speed and air gap in this model. All calculated soft meauremental results were compared with results of finite element method using ANSYS software. The compared result shows that the eddy current density of copper conductor plate of eddy-current driver calculated by soft measurement model can legitimately replace the numerical method with the approximate accuracy with mean error of less than 2% which provides important evidence for the calculation and the optimal design of PM eddy-current driver.

disk type permanent magnet eddy-current driver; eddy current soft measurement; analytical analysis; finite-element method

2015-01-29

辽宁省科技创新重大专项资助项目(201309001)

时统宇(1988—)，男，博士研究生，研究方向为永磁驱动器的建模和分析；

王大志(1963—)，男，博士，教授，博士生导师，研究方向为传动系统设备建模、控制及优化设计；

时统宇

10.15938/j.emc.2016.11.003

TM 153

A

1007-449X(2016)11-0018-07

石松宁(1982—)，女，博士研究生，研究方向为永磁驱动器的优化设计；

郑 迪(1988—)，女，博士研究生，研究方向为永磁驱动器的建模和设计；

李 召(1986—)，男，博士研究生，研究方向为永磁驱动器的建模和优化。