分散式风电场不同时间等级的多目标无功优化控制

邢作霞， 颜宁， 肖婉秋， 厉伟

(1.沈阳工业大学 电气工程学院，辽宁 沈阳 110870；2. 国网沈阳市于洪区供电公司，辽宁 沈阳 110141)



分散式风电场不同时间等级的多目标无功优化控制

邢作霞1， 颜宁1， 肖婉秋2， 厉伟1

(1.沈阳工业大学 电气工程学院，辽宁 沈阳 110870；2. 国网沈阳市于洪区供电公司，辽宁 沈阳 110141)

针对具有一定动态无功调节能力的双馈式风力发电机组构成的分散式风电场，为解决其经济稳定运行，提出一种包含风功率预测的不同时间尺度多目标无功优化控制方法。考虑风速变化相关性分组-单机预测风电机组无功输出情况，通过风电机组和SVC共同补偿电网无功需求；根据风电预测无功功率信息，采用多目标无功控制快速有效调节其输出功率以跟踪无功补偿指令。为减少风电场内设备动作次数，选取不同时间级的控制，目标为分钟级无功控制以有功网损最小为优化目标，秒级的无功控制以电压偏差最小、电压稳定裕度最大、短时闪变最小为综合优化目标，毫秒级的无功控制以机组变流器的瞬间最大无功支撑能力为优化目标进行无功分配。工程算例证明所提策略有效的降低网损、提高电压支撑能力并保证电网正常的运行。

分散式风电场；功率预测；多目标无功优化;不同时间尺度；模拟退火-粒子群算法

0 引 言

风电作为电源具有随机性和间歇性，随着更多大容量风电场的投入运行，风电并网等技术问题越来越突出，集中式大电网对负荷变化的适应能力差，运行不够灵活。在此背景下，国家提出了发展分散式风电的政策[1-5]。

分散式发电形式相比于集中式发电有以下特点：单机容量小，多机成组并列，逐级升压送入主电网，发电设备众多，控制复杂；一般接入原有配电网，接近用户终端，易于本地消纳；风电渗透率增加，潮流双向流动，风电的随机波动性将引起电网电压和频率不稳定问题[6-9]。由此看来，针对分散式风电的网络规划、调度、安全运行等问题需要迫切解决、深入研究。

分散式风电场接入配电网时，传统的投切电容器不能实现动态无功调节，过多应用连续补偿装置将加大初始投资成本，因此，分散式风电场多采用具有无功调节能力的双馈式风力发电机组，其无功优化问题实质上就是系统的结构参数及负荷情况给定时，通过对某些控制变量的优化，所能找到的在满足所有指定约束条件的前提下，使系统的某一个或多个性能指标达到最优时的无功调节手段。对电网进行无功优化可以控制电压水平和降低有功损耗等，从而改善电能质量等目的[10-11]。

针对风功率预测方面，目前多为采用物理和统计方法进行预测，主要研究范围在中长期的风速整场预测，如文献[12]提出了基于粗糙集理论的中长期风速预测，预测时间长，准确率低；文献[13]采用模型对风电场风速进行短期预测，其未能考虑风场内风速变化相关性；文献[14]考虑流动相关性对风电场机组分组功率预测，一定程度上提高预测精度。本文在上述研究基础上提出一种虑风电场内风速变化相关性分组-单机预测方法，实时操作性强，在节约计算时间同时提高预测精度。

针对风电场无功优化控制方面，多采用无功补偿装置进行补偿，控制结构单一。如文献[15]针对风电场的无功控制及优化研究，采用等功率因数原则进行无功分配，但由于各台机组有功出力情况不同，导致部分机组无功出力过早饱和；文献[16-17]提出双馈风力发电机(double fed induction generator, DFIG)与静止无功发生器(static var generator, SVG)协调无功优化控制，在降低损耗的同时增加了初始成本投资，优化目标单一；文献[18-21]提出改进粒子群优化算法在多目标无功优化，是一种多目标、多变量、多约束的混合非线性规划问题，但研究重点在于改进算法对多目标求解。本文在以上研究基础上提出不同时间等级多目标无功优化控制，通过工程算例证明此控制方法有效的降低网损、提高电压支撑能力并保证电网正常的运行。

1 分散式风电场无功控制

分散式风电场可看成一个可调度的发电厂，为发挥其协调调度能力，提出考虑风电场内风速变化相关性分组-单机预测多目标无功优化控制。利用风速相关性预测各台风机的功率，结合当地电网特性，进行风电场级的无功优化控制。分散式风电场无功控制如图1所示。

图1 不同时间等级多目标无功控制Fig.1 Multi-timescale multi-objective reactive power optimization

1.1 基于风速变化相关性分组-单机预测

考虑分散式风电场内同一时刻机组的风速及输出功率具有一定相关性，综合考虑风电场主导风向、机组海拔高度等因素，将风电场按功率相关性进行分组，使分组区域内机组出力情况相似。但由于分散式风电场风机数目较少，接入点较为分散，受到尾流和迟滞效应影响较大，同一时间捕获的风速不同，进而根据风速相关性进行功率预测。基于风电场内风速变化相关性分组-单机预测如图2所示。

图2 基于风速变化相关性分组-单机预测Fig.2 Packet-single prediction based on the correlation of wind speed variation

假设同一组别内风速相同，根据风电场主导风向、机组海拔高度等因素进行分组风电功率预测；分组预测后，在每组中选取一台机组所在位置为中心位置，并综合考虑机组间地理距离，尾流和迟滞效应影响，根据相关系数计算风速相关性，进而预测出单台机组功率。

1.2 风电场级无功补偿控制论文格式基本要求：

根据分散式风电场接入点不同，考虑经济有效运行，协调运用双馈风力发电机组与无功补偿装置进行无功补偿，补偿原则如下：

通过SCADA检测控制和采集系统测出风场风速，每台风机定子侧电压、定子电阻、励磁感抗、相角和每台风机的出口的有功功率，无功功率等数据，然后将这些数据通过通讯线缆发送控制中心，控制中心将数据与无功预测极限对比。

当需求量大于总无功预测极限时，将各台机组按最大无功输出运行，剩余无功缺少额由SVC补偿；

单台输出无功功率输出极限为

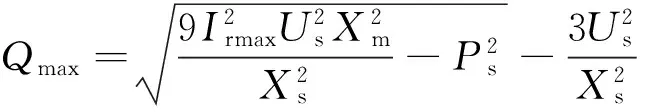
(1)

式中：Imax为转子最大电流值(一般取额定电流值的150%)；Us为定子电压有效值；Xm为励磁感抗；Xs为折算后定子侧电抗值；Ps为定子的有功功率。

当需求量小于总无功预测极限时，按不同时间尺度进行多目标无功优化控制，整定各台机组无功输出值。

1.3 不同时间尺度多目标无功优化

1)分钟级控制

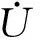
(2)

式中：NB为参与损耗计算的支路总数；Ploss为区域有功网损；Ui和Uj分别为节点i和节点j的电压幅值；δij为节点i和j的相角差且δij=δi-δj；Gij为支路电导。

2)秒级控制

在下一个分钟级周期开始前，进行秒级控制，如图3所示，将采集到的汇集点电压与调度中心参考电压值进行比较，得到电压偏差值,为了防止设备的频繁调节，设置电压死区范围。

根据国家标准GB/T12326-2008的要求，当满足长时闪变小于0.25时则可以不需要对短时闪变进行调节。若电压偏差值在死区范围内并且短时闪变满足国标要求，则不需要进行优化，保持上一周期的优化方案，等待下一个分钟级控制周期。

图3 秒级控制策略Fig.3 Seconds grade control strategy

若超出死区控制，针对秒级的无功优化控制，系统将以短时闪变最小、电压偏差最小为综合优化目标进行电压控制，控制目标为：

f2=min(c1Pst+c2ΔU)。

(3)

其中，

(4)

式中：Psti为第i个节点的短时闪变；RL和XL电网阻抗的电阻和电抗分量；ΔPi和ΔQi为风电场节点的有功和无功变化量；dlim为Psti=1时的电压变动参数。Ui为节点i的实际电压，Urefi为期望电压值；ΔUimax=Umax-Umin为最大允许电压偏差；NB为节点数；ΔUi为第i个接入点电压的偏差；c1，c2为权重系数，且c1+c2=1。

3)毫秒级控制

当在下一个秒级周期开始前，进行毫秒级控制，针对毫秒级的无功优化控制，系统以机组变流器的瞬间最大无功支撑能力为目标，目标函数为

(5)

若满足优化目标则不需要优化，保持上一周期的优化方案，等待下一个秒级控制周期。

4)约束条件

潮流的约束条件如下：

(6)

式中：PMi为风电场第i节点发出的有功功率；QMi为风电场第i节点发出的无功功率；PNi为风电场第i节点负荷的有功功率；QNi为风电场第i节点负荷的无功功率；Ui为风电场第i节点的电压；Uj为风电场第j节点的电压；Bij为风电场第i节点和第j节点之间的电纳；N为风电场的节点集合；n是以风电场第i节点为起点所有支路的右端节点集合。

状态变量的约束条件如下：

(7)

控制变量的约束条件如下：

QiminQiQimax。

(8)

2 SA-PSO在多目标无功优化中求解

通过模拟退火-粒子群算法(particle swarm algorithm based on simulated annealing, SA-PSO)对上述不同时间尺度多目标无功优化进行求解，得出每台机组无功输出值，并与粒子群算法(particle swarm optimization, PSO)进行比较，得出系统有功网损不同收敛特性，进而比较两种算法优劣性。

在物理系统中，SA-PSO是在模拟整个退火中随机搜索过程，执行步骤包括产生、新解、判断到接受或舍弃。

其求解不同时间尺度多目标无功优化的流程如下：

1)根据已设定的目标函数、约束条件对一群粒子进行一系列初始化。设粒子规模为种群m，种群中包括各个粒子的速度、位置。与此同时，随机初始化SA-PSO中各个参数，给定退火速度为α，初始温度T0，退火终止温度T1；

2)利用分散式风电场运行数据、负荷数据,在满足约束条件下进行运行模拟数据分析，每分钟更新数据，求取系统数据可变情况下优化无功输出结果；

3)计算适应度函数，选出所经历过的最好位置Pbest；

4)粒子经历过的最好位置标记索引号为Gbest，将每个粒子适应度与其比较，当存在新的最好位置，更新索引号；

5)将所有粒子位置限定在位置变化区域以内，更新各个粒子的速度、位置，让其不超出此位置；

6)设定适应度函数变化量为ΔE，计算任意2个位置ΔE，若ΔE≤0,接受新的值，重新设定新的位置；若exp(-ΔE/T)>rand(0, 1)，同样接受新的值，重新设定新的位置；否则拒绝,不重新设定新的位置；

7)若接受新值，则降低一定比例温度，否则，不降温；

8)若满足这种收敛条件，则输出粒子群中最优位置，得出最优解；若不满足此收敛条件,则返回步骤2，重新进行下一次收敛运算[22]。

3 工程算例分析

采用辽宁省某分散式风电场，该风电场具有分散式风电场场区地形条件，安装了31台1.5 MW的双馈异步发电机，风机出口电压为690 V，额定同步转速为1 500 r/min。每台风机采用1套YB27-1600/10型美式箱变升压，风电场分4个区域，每个区域的风机各自通过10 kV集电线路接入就地66 kV变电站，并在10 kV母线上安装一台容量为5 MVA的SVC。将此风场一年功率数据作为预测基础(时间：2014年5月至2015年4月)，通过Matlab建立风电场电气模型，并将其接入IEEE14节点系统进行测试，该系统包含20条支路，支路4～7、4～9、5～6为可调变压器支路，节点1、2、3、6、8为发电机节点(其中1为平衡节点，2、3、6、8为P-V节点)，其余为P-Q节点；9为无功补偿节点。节点电压上下限位1.10和0.95；分散式风电场通过4个节点接入，节点5接入6台风力发电机组；节点9接入10台风电机组和一台容量为5 MVA的SVC；节点11接入10台风电机组；节点14接入5台风力发电机组。

将基于风速变化相关性分组-单机预测结果与物理统计方法进行对比分析，如图4所示，前者精度较高，偏差率随着时间推移波动不大，有效提高预测精度。

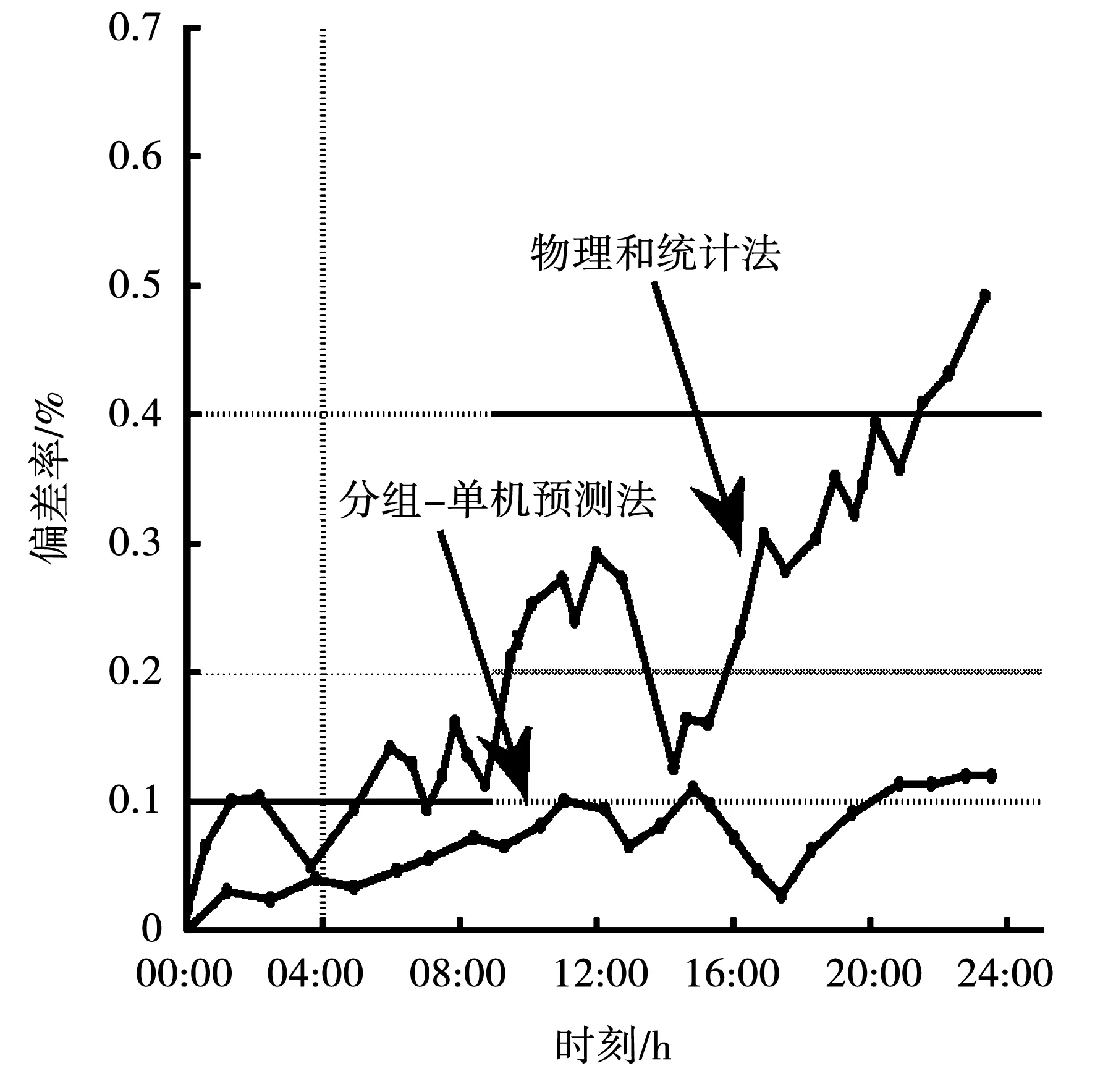
图4 不同预测方式偏差率对比结果Fig.4 Contrast results of power deviation rates

为减少随机波动性对算影响，本文将PSO算法与SA-PSO算法分别迭代100次，根据图5可以看出经SA-PSO算法优化后，有功网损明显下降，网损平均下降率为10.31%，下降率较PSO算法明显提高。

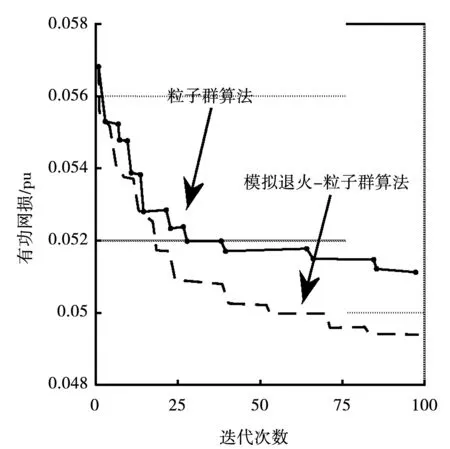
图5 IEEE14节点系统有功网损收敛特性Fig.5 Performance characterastics for IEEE14-bus system

采用PSO算法与SA-PSO算法对不同时间等级多目标进行无功优化，平均优化结果如表1所示。优化结果较PSO算法明显提高。

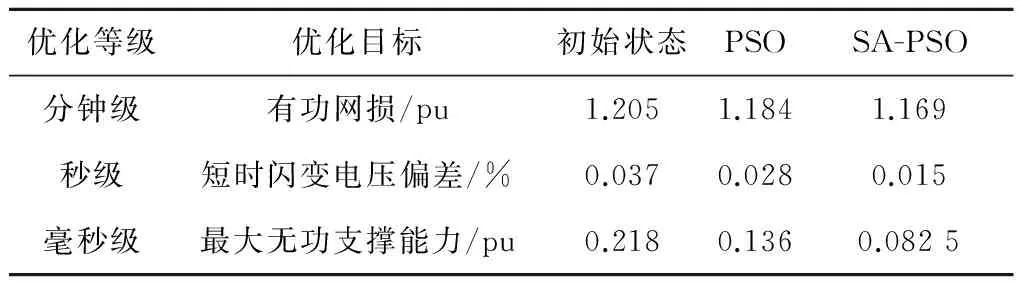
表1 IEEE14 节点系统平均优化结果

仿真计算IEEE14节点系统，发现3个目标是相互冲突、存在竞争，目标基本不可能同时达到最优解，目标同时达到最优的可能性很小。根据对3种优化目标需求选择权重，求解电力系统多目标优化问题。

4 结 论

本文针对分散式风电场特点，考虑风电场内风速变化相关性进行分组-单机预测出力，根据风电机组实际无功需求综合调节风电机组和SVC，实现不同时间等级多目标无功优化控制。通过工程算例分析，得出如下结论：

1)考虑分散式风电场风速相关性，对风电机组进行分组-单机预测，与物理统计方法对比，有效提高预测精度，是目前较为先进预测方法；

2)通过无功需求量与总预测极限对比，提出两种不同形式无功分配方式。当需求量小于总无功预测极限时，按不同时间尺度进行多目标无功优化控制，通过工程算例分析，其有效的减少设备调节次数，降低网损、提高电压支撑能力并保证电网正常的运行;

3)将PSO算法与SA-PSO算法分别应用于不同时间尺度多目标优化中，发现SA-PSO优化结果较PSO算法明显提高。

[1] 李俊峰. 中国风电发展报告[M]. 北京: 中国环境科学出版社, 2012: 3-38.

[2] 孙伟卿, 王承民, 张焰, 等. 电力系统综合节能的有功与无功功率协调优化[J]. 电机与控制学报, 2010, 14(7): 41-47.

SUN Weiqing, WANG Chengmin, ZHANG Yan, et al. Reactive power coordinated optimization in power systems comprehensive energy saving[J]. Electric Machines and Control, 2010, 14(7): 41-47.

[3] HEYDARI H, MOGHADASI, A H. Optimization scheme in combinatorial UPQC and SFCL using normalized simulated annealing[J]. IEEE Transactions on Power Delivery, 2011, 26(3): 1489-1498.

[4] 倪喜军, 赵剑锋, 曹武, 等. 开关损耗优化的级联型逆变器全区域空间矢量调制策略[J]. 电工技术学报, 2012, 27(4): 101-109.

NI Xijun, ZHAO Jianfeng, CAO Wu, et al. Switching loss optimized svpwm algorithm for cascade multilevel inverters in all region[J]. Transactions of China Electro Technical Society, 2012, 27(4): 101-109.

[5] 何娜, 胡安, 高强, 等. 大容量混合有源滤波器多目标优化设计[J]. 电机与控制学报, 2010, 14(11): 49-57.

HE Na, HU An, GAO Qiang, et al. Multi-objective optimal design of hybrid active power filter[J]. Electric Machines and Control, 2010, 14(11): 49-57.

[6] 朱雪凌, 张洋, 高昆, 等. 风电场无功补偿问题的研究[J]. 电力系统保护与控制, 2009, 37(16): 68-72.

ZHU Xueling, ZHANG Yang, GAO Kun, et al. Research on the compensation of reactive power for wind farms[J]. Power System Protection and Control, 2009, 37(16): 68-72.

[7] 贾俊川, 刘晋, 张一工. 双馈风力发电系统的新型无功优化控制策略[J]. 中国电气工程学报, 2010, 30(30): 87-92.

JIA Junchuan, LIU Jin, ZHANG Yigong. Novel reactive power optimization control strategy for doubly fed induction wind power generation system[J]. Proceedings of the CSEE, 2010, 30(30): 87-92.

[8] 陈宁, 朱凌志, 王伟. 改善接入地区电压稳定性的风电场无功控制策略[J]. 中国电机工程学报, 2009, 29(10): 102-108.

CHEN Ning, ZHU Lingzhi, WANG Wei. Strategy for reactive power control of wind farm for improving voltage stability in wind power integrated region[J]. Proceedings of the CSEE, 2009, 29(10): 102-108.

[9] 王旭强, 刘广一, 曾沅,等. 分布式电源接入下配电网电压无功控制效果分析[J]. 电力系统保护与控制, 2014, 42(1):47-53.

WANG Xuqiang, LIU Guangyi, ZENG Yuan, et al. Analysis on the effects of Volt/Var control method considering distributed generation[J]. Power System Protection and Control, 2014, 42(1): 47-53.

[10] 张平, 刘国频, 曾祥君, 等. 风电场无功电源的优化配置方法[J]. 电力系统保护与控制, 2008, 36(20): 33-37.

ZHANG Ping, LIU Guopin, ZENG Xiangjun, et al. Optimal allocation of reactive power source for wind farms[J]. Power System Protection and Control, 2008, 36(20): 33-37.

[11] PERDANA A, CARLSON O. Factors influencing design of dynamic reactive power compensation for an offshore wind farm[J]. Wind Engineering, 2013, 33(3): 273-286.

[12] 高爽, 冬雷, 高阳, 等. 基于粗糙集理论的中长期风速预测[J]. 中国电机工程学报, 2012, 32(1): 32-37.

GAO Shuang, DONG Lei, GAO Yang, et al. Mid-long term wind speed prediction based on rough set theory[J]. Proceedings of the CSEE, 2012, 32(1): 32-37.

[13] 卿湘运, 杨富文, 王行愚. 采用贝叶斯-克里金-卡尔曼模型的多风电场风速短期预测[J]. 中国电机工程学报, 2012, 32(35): 107-114.

QING Xiangyu, YANG Fuwen, WANG Xingyu. Short-term wind speed forecasting for multiple wind farms using Bayesian Kriged-kalman mode[J]. Proceedings of the CSEE, 2012, 32(35): 107-114.

[14] 阎洁, 刘永前, 韩爽,等. 考虑流动相关性的风电场机组分组功率预测方法[J]. 现代电力, 2015, 2(1): 25-30.

YAN Jie, LIU Yongqian, HAN Shuang et al. power prediction method for grouping wind turbine generations by considering flow correlation. Modern Electric Power 2015, 2(1): 25-30.

[15] 王琦, 袁越, 陈宁, 等. 多风场接入局部电网的无功协调分配方法[J]. 电力系统保护与控制, 2012, 40(24): 76-83.

WANG Qi, YUAN Yue, CHEN Ning,et al. The cooperating distribution methods of reactive power in multi-wind farms integrated region[J]. Power System Protection and Control, 2012, 40(24): 76-83.

[16] 厉伟, 颜宁, 邢作霞,等. 分散式风电场DFIG与SVC协调无功控制策略 [J]. 电工电能新技术, 2014, 33(7): 18-22.

LI Wei, YAN Ning,XING Zuoxia,et al.Strategy of reactive power control for distributed wind farm operation using SVC and DFIG[J]. Advanced Technology of Electrical Engineering and Energy,2014, 33(7):18-22.

[17] 赵利刚, 房大中, 孔祥玉, 等. 综合利用SVC和风力发电机的风电场无功控制策略[J]. 电力系统保护与控制, 2012, 40(2): 45-50.

ZHAO Ligang, FANG Dazhong, KONG Xiangyu,et al. A strategy of reactive power control for wind farm operation using SVC and DFIG[J]. Power System Protection and Control, 2012, 40(2): 45-50.

[18] 程杉, 陈民铀, 黄薏宸. 含分布式发电的配电网多目标无功优化策略研究[J]. 电力系统保护与控制, 2013, 41(10): 45-50.

CHENG Shan, CHEN Minyou, HUANG Yichen. Multi-objective reactive power optimization of distribution system penetrated with distributed generation[J]. Power System Protection and Control, 2013, 41(10): 45-50.

[19] 罗毅, 多靖赟. 基于免疫记忆克隆选择算法的多目标无功优化[J]. 电力系统保护与控制, 2012, 40(24): 65-70.

LUO Yi, DUO Jingyun. Multi-objective reactive power optimization based on immune memory colonial selection algorithm[J]. Power System Protection and Control, 2012, 40(24): 65-70.

[20] 唐贤伦, 张衡, 唐海, 等. 多Agent结构的混沌PSO在无功优化中的应用[J]. 电机与控制学报, 2013, 17(6): 16-22.

TANG Xianlun, ZHANG Heng, TANG Hai, et al. Chaos particle swarm optimization algorithm based on multi-agent architecture for reactive power optimization[J]. Electric Machines and Control, 2013, 17(6): 16-22.

[21] 范坚坚, 吴建华, 黎宪林, 等. 永磁同步电动机磁钢的多目标微粒群算法优化[J].电机与控制学报, 2009, 13(2): 173-178.

FAN Jianjian, WU Jianhua, LI Xianlin, et al. Multi-objective particle swarm optimization of alnico in permanent magnet synchronous motor[J]. Electric Machines and Control, 2009,13(2):173-178.

[22] 唐权, 吴耀武. SA-PSO在水火电混合电力系统电源规划中的应用[J]. 高电压技术, 2006,32(4): 104-107.

TANG Quan, WU Yaowu. Generation expansion planning of hydro-thermal power system based on SA-PSO[J]. High Voltage Engineering, 2006,32(4):104-107.

(编辑：张 楠)

Multi-timescale multi-objective reactive power optimization of dispersed wind farm

XING Zuo-xia1， YAN Ning1， XIAO Wan-qiu2， LI Wei1

(1.School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China; 2.State Grid Corporation Yuhong District Electric Power Company, Shenyang 110141, China)

For distributed wind farm consisting of DFIG with dynamic reactive power regulation,in order to achieve economic and stable operation, a multi-objective reactive power optimization based on wind power forecasting was proposed. Considering the change of the wind speed to predict the reactive power output based on the correlation grouping-single unit. The reactive power demand of the power network was compensated by wind turbine and SVC. According to the wind power forecasting, the multi-timescale multi-objective reactive power optimization wind turbines were adopted considering reactive power forecasting and wind speed fluctuation to track reactive power demand. Choosing different time level control objectives for reducing the numbers of equipment movements, minute grade optimization target is minimum active power loss, seconds grade optimization target are maximum voltage stability margin and minimum short flicker, millisecond grade optimization target is maximum reactive power support capability. Engineering example proves that the proposed strategy reduces the transmission losses of wind farm and improves the ability of supporting voltage effectively.

dispersed wind farm; power forecasting; multi-objective reactive power optimization; multi-timescale; SA-PSO

2015-08-11

国家能源局项目(NY20150303)

邢作霞(1976—)，女，博士，副教授，研究方向为电力系统分析与新能源发电；

颜 宁(1988—)，女，博士研究生，研究方向为分散式风电场无功优化、风储电站经济性分析；

颜 宁

10.15938/j.emc.2016.11.007

TM 614

A

1007-449X(2016)11-0046-07

肖婉秋(1967—)，女，硕士，高级工程师，研究方向为微网协调控制技术；

厉 伟(1962—)，男，博士，教授，博士生导师，研究方向为高电压试验技术、绝缘在线检测等。