等效正弦的分级变频软启动器研究与设计

童军， 乔江， 郭昌永， 刘丽娟， 朱理鹏

(1.西安科技大学 电气与控制工程学院，陕西 西安 710054；2.甘肃容和矿用设备集团西安分公司，陕西 西安 710043)



等效正弦的分级变频软启动器研究与设计

童军1， 乔江1， 郭昌永2， 刘丽娟1， 朱理鹏1

(1.西安科技大学 电气与控制工程学院，陕西 西安 710054；2.甘肃容和矿用设备集团西安分公司，陕西 西安 710043)

针对传统软启动器起动转矩过小而无法满足重载起动的问题，利用分级变频原理，同时借鉴恒压频比的电机变频调速理论，提出了一种基于等效正弦的分级变频软启动控制方法，可以降低电机定子相电流的谐波含量，减小电机在分级变频软启动过程中的转矩脉动，达到平稳起动重载的目的。通过搭建基于等效正弦的7阶段控制系统仿真模型，验证了该理论的合理性。在此基础之上，研制了分级变频软启动器实验样机，试验结果表明，所提出的方法可有效的改善电机的起动电流波形，与仿真结果吻合。

感应电机；软启动；分级变频；等效正弦

0 引 言

异步电机作为现代工业设备的主要动力来源，起动问题备受关注。一般情况下，大功率的电机直接起动，会对电网及设备产生较大的电流冲击。传统的解决办法是通过机械开关如接触器或继电器，人为地改变电机的接线方式或电流流通通道来达到降压的目的。这种起动方式有助于避免大功率的电机在局域电网上的起动产生不利影响，但是它们只是相对减小了冲击的强度，并未在本质上消除冲击问题。而且，起动装置大多采用的是继电器，接触器等有触点系统，所以无法保证起动电压线性平滑的变化，带来的缺陷就是负载适应能力差、起动电流存在二次冲击、维修不便等。交流调压软启动器的出现避免了这一弊端。目前，交流调压除了单一的调压功能之外，可以引入双斜坡，构成双斜坡电压软起动，可以引入电流闭环，构成限流软起动；但是，这些软启动器一个显而易见的缺陷是限制了起动电流，却不能保证重载起动[1]。所以，如何在降低起动电流同时，保持较高的起动转矩成为了国内外专家所探讨的一个重要话题。

分级变频软启动器的出现，使电机的起动实现了类似于离散VVVF变频器的起动效果，有效提高三相感应电机的初始起动转矩。而电机在分级变频软启动时，往往抖动比较剧烈，分析原因为电机定子电流中含有较大的谐波分量[2-3]。本研究旨在将等效正弦原理应用到分级变频理论中，设计一台基于等效正弦的分级变频软启动器，从而减少电流中的谐波含量，使电机达到较好的起动效果。

1 分级变频原理

分级变频是通过周波控制，使工频输入的某些半波导通，某些半波截止，从而增加输出电压的周期以降低频率。由于周期的改变都是整数倍关系，所以分频也是整数倍关系，分级变频软启动器起动过程就是在这些频段的切换过程，所以分级变频也称离散变频[4]。

图1展示了单相分级变频过程，频率从3.85→7.14→12.5→16.7→25→50 Hz分级变化。但对于三相供电系统的分级变频要比单相复杂的多，需要考虑分频后电源的相序、相位问题。

三相供电电源A相、B相、C相，频率为50 Hz，角频率为ωnet，电压幅值为U1。其电压瞬时值可表示为：

(1)

经v分频后得到新频率下的三相电压基波瞬时值为：

(2)

其中ωnet=νωsub。

图1 单相3.85→7.14→12.5→16.7→25→50 Hz分频波形示意图Fig.1 Waveform of single-phase discrete frequency for 3.85→7.14→12.5→16.7→25→50 Hz

设A相电压的相位φA=0，可知：

(3)

其中k=0,1,2……。

当新的频率下的三相电压正序对称时，ν=3k+1，即ν为4、7、10、……；负序对称时ν=3k-1，即ν为2、5、8、11、……；当ν=3k时只有零序分量。而且，对于正、反相序对称的分频，奇分频可以获得相位和幅值平衡且在时间轴上平衡的波形，而偶分频其波形在时间轴上不平衡。

选择分频级数时[5]应考虑完全平衡即相位、幅值及时间轴均平衡的分频方式，这在低频段容易实现，如起动时选择正相序平衡的13分频和7分频。但在高频段(这里指2-4分频)，由于处在低频和工频的过渡频段，则不得不采用不完全平衡分频方式，如4分频和3分频及完全负序对称的2分频；而且从2分频到工频这一过程跨度较大，电机在2分频下运行时的理想转速仅为电机额定理想转速的一半，因此不可直接切换到工频，否则转差率过大，必然产生过大的电流冲击。为避免此情况，需要对电压进行控制。采用交流调压起动方式。对于所选频段没有满足正序对称要求的，则应按照供电电源中正序分量最大，负序分量最小的方式来选择相位组合，保证电动机获得最大正向电磁转矩。

采用对称分量法对三相3分频和2分频的相位进行数学分析，如式(4)所示：

(4)

通过计算可得， 16.7 Hz时(0°，260°，100°)、(0°，260°，160°)和(0°，200°，100°)，25 Hz时(0°，210°，60°)、(0°，210°，150°)、(0°，300°，150°)满足正序分量最大，负序分量最小的要求。

根据以上分析，整个分级变频软启动过程采用7段完成，即f/13→f/7→f/4→f/3→f/2→交流调压起动→f。切换时应遵循以下原则：1)分级变频软启动过程中需保证正弦曲线的连续性；2)所选取的各频率基波需保证正负半周交替变换；3)切换前后需保证各频段的转矩平稳过渡，以减小转矩振荡。基于上述原则，最简单有效的方法就是采用整周期或者半周期切换，或者改进为准整周期或准半周期切换。

2 等效正弦控制策略

电机起动过程最重要的性能指标是起动转矩倍数和起动电流倍数，要求电机在起动时以最小的起动电流仍然可以获得较大的起动转矩。根据电机学理论及异步电机的T型等效电路，如图2所示。可得电机的电磁转矩为

(5)

刚起动时，转速n=0，转差率s=1，起动转矩为

(6)

起动电流为

(7)

图2 异步电动机T型等效电路Fig.2 T-type equivalent circuit for asynchronous motor

采用常规的分级变频即每一频段α固定的触发方式得到的电压波形为非正弦，且谐波含量较大。根据电力电子学中面积等效原理[6]，可以按照某种控制规律调节触发角的大小，使得输出电压为等效正弦，即为本文提出的等效正弦控制方法，从而减小谐波以及转矩脉动对电机的冲击。

图3 7分频(7.143 Hz)时电压输出波形Fig.3 Voltage output wave diagram of 7 hierarchical frequency

等效正弦控制方法[7]就是使实际波形近似等效为正弦波，降低输出波形的谐波含量。而对于某一频段来说，工频正弦波是其整数次谐波，而且含量较大，这是因为每一频段波形都是由工频正弦波斩波得到的。要想降低工频正弦对各频段的影响或者提高各频段的基波含量，可以通过改变一个周期内各触发角的大小来实现。如图3所示，是对工频电压7分频得到的7.143 Hz频率的示意图。图中等效电压为7分频后的基波，且uv=Uvmsinωvt；工频电压为u1=U1msinω1t。结合VVVF原理及等效正弦控制原理可得：

(8)

3 仿真分析

借助于SIMULINK工具搭建仿真平台[8-9]，其中异步电动机PN=5.5 kW、UN=380 V、Rs=1.55 Ω、Rr=1.62 Ω、Ls=9.2 mH、Lr=12.5 mH、Lm=69.31 mH、J=0.02 kg·m2、nN=2 900 r/min,对基于等效正弦的分级变频控制进行研究，起动过程中各级晶闸管触发角根据等效正弦原理计算得到，采用频率3.85Hz→7.14Hz→12.5Hz→16.7Hz→25Hz→交流调压起动→50Hz的起动方案。起动过程仿真波形如图4所示。

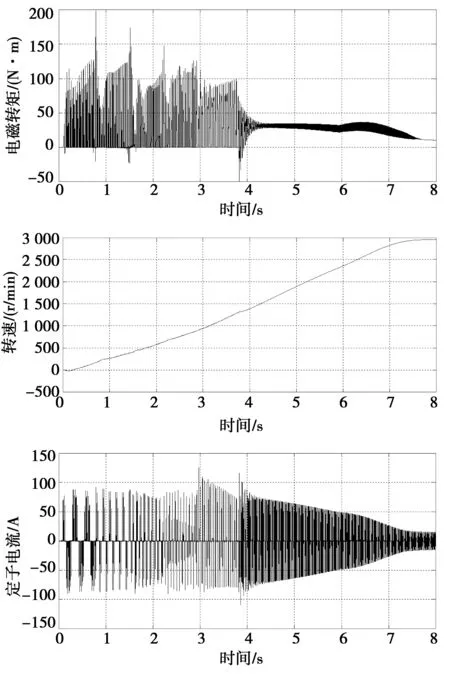
图4 分级变频软启动转矩、转速和定子电流仿真波形Fig.4 Simulation waveforms of torque,speed and stator current are under discrete frequency soft start

由于固定角分级软启动和等效正弦分级软启动起动过程类似，为了能直观的表达两者的差异，利用SIMULINK中FFT Tools分别对两种方式得到的7分频时定子电流波形进行频谱分析，如图5所示。

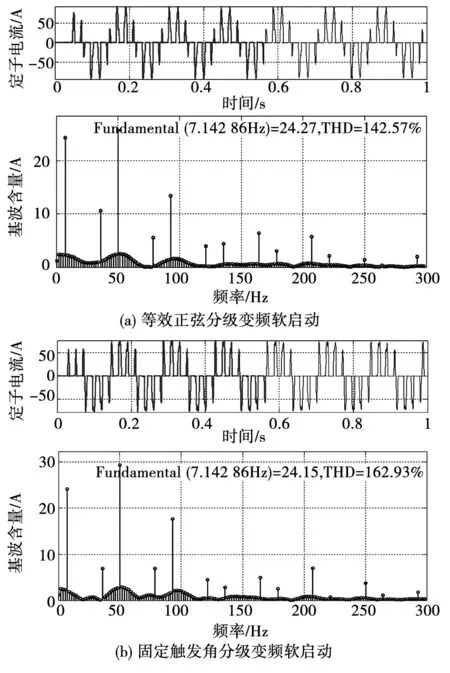
图5 定子电流频谱分析Fig.5 Stator current spectrum analysis

由分析可知，在基波含量接近的情况下，采用等效正弦触发方式，THD由未采用时的162.93%变为142.57%，定子电流中的谐波含量明显降低。由此可知该方法优化了定子电流波形，从而一定程度上可以抑制寄生转矩带来的电磁震荡。

4 样机设计与实验

4.1 控制系统设计

样机设计所采用的控制器为Microchip公司的16位高性能控制器dsPIC6014A-301/PF，主电路与传统的软启动器相同。控制电路主要包括：电压同步及相序检测、电源电路、驱动电路、电流检测电路、接触器控制电路及按键与显示。软启动样机控制系统[10]框图如图6所示。

图6 分级变频软启动器控制系统框图Fig.6 Control system diagram of discrete frequency soft starter

4.2 电压同步及触发方案

主回路六路晶闸管的触发脉冲需与电源电压保持严格的相位关系，即为同步，因此在设计当中，同步电压检测是至关重要的一环。由于本系统通过触发晶闸管不单要实现相控调压，更为重要的还要根据分级变频的触发规则确定相应半波是否触发导通以及按等效正弦原理分配触发角大小。脉冲触发环节如图7所示。

图7 同步及脉冲触发框图Fig.7 Diagram of synchronization and trigger pulse

对于触发脉冲来说，有双窄脉冲触发和宽脉冲触发。采用双窄脉冲可能会出现第二个窄脉冲不触发，不能保证工作的可靠性，因此不采用。若采用宽脉冲，虽具有较强的抗扰动性能可保证晶闸管准确触发，但却需要较大的输出功率和较大容量的变压器，选择不合适容易使脉冲变压器饱和，所以也不采用。因此采用具有足够功率的窄脉冲序列，代替一定宽度的触发脉冲来触发六路晶闸管，如图8所示，既可以保证触发的可靠性，又可以防止脉冲变压器的饱和。

4.3 实验结果

对一台额定电压380/660 V，额定电流11 A，额定功率5.5 KW，额定转速2 900 r/min，三相鼠笼型感应电机，带额定负载进行不同类别的软启动实验(斜坡电压起动与分级变频起动)，以及不同触发方式下的分级变频软启动实验，实验所得波形如图9所示。

图8 晶闸管触发脉冲序列Fig.8 SCR trigger pulse sequences

图9 实验波形Fig.9 Experimental waveforms

分级变频的分频方式采用的分频数依次为13、7、4、3、2、斜坡电压软启动，变频部分起动时间为5 s, 该段时间电流有效值很小,最大为1.5 IN。同一时间段内，斜坡电压软启动却一直处于堵转状态。由此可知分级变频软启动带负载能力强，在重载情况下，无疑是较好的选择。

对于不同触发方式的分级变频来说，交流调压器输出电流波形有着明显的差异，图10为局部放大的7分频电流波形。较之固定角的触发方式来说，等效正弦分级软启动遵循正弦面积等效原理呈现近似正弦形态，此形态有助于减少电流中的谐波含量，抑制异步电动机分级变频起动时出现的电磁转矩振荡。

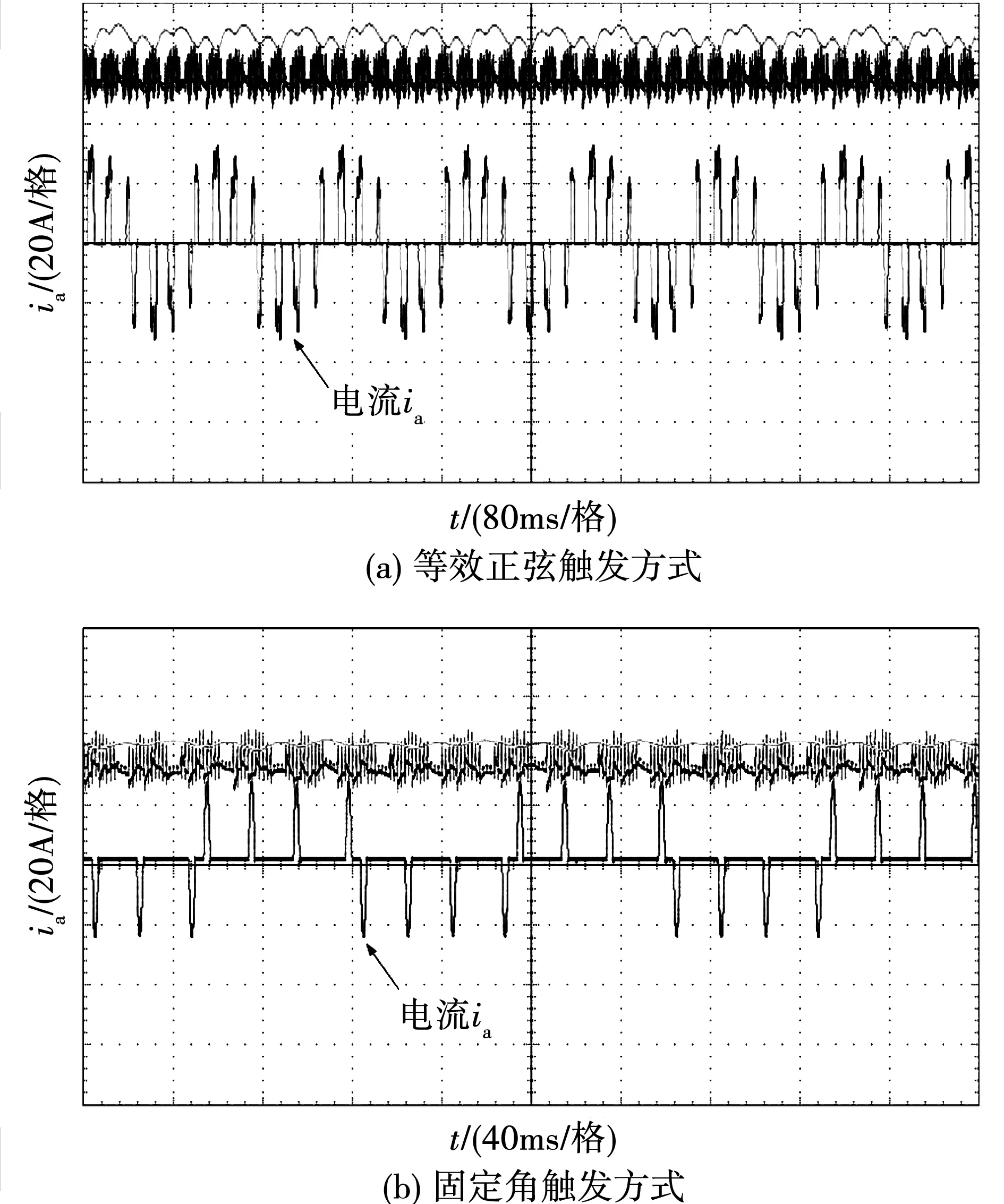
图10 分级变频7分频局部电流波形Fig.10 Local current of 7 hierarchical frequency

5 结 论

传统的软启动器由于起动转矩小而限制了其应用范围，本文通过对分级变频基本原理的分析与研究，融入等效正弦控制策略，实现了电机的高转矩起动。根据仿真及相关的实验验证了该理论的正确性及有效性。在不改变原有软启动器结构的条件下，通过改变控制策略可实现等效正弦的分级变频起动。该方法不仅满足一般负载及重载的起动要求，而且一定程度改善了电机定子电流波形，使电机能平稳起动，拓宽了软启动器的应用范围，具有较高的实用价值。

[1] 严垚, 王宏华. 异步电动机离散变频软启动技术的发展[J]. 机械制造与自动化, 2012, 41(6):196-199.

YAN Yao, WANG Honghua.Development of discrete variable frequency induction motors soft starter[J].Machine Building & Automation, 2012, 41(6):196-199.

[2] 杨顺昌, 廖勇, 余渝. 考虑谐波影响后交流励磁电动机电磁转矩的分析与计算[J]. 电工技术学报, 2003, 18(1):5-9.

YANG Shunchang, LIAO Yong, YU Yu. Analysis and calcualation of electromagnetic torques for AC excited motors incorporating the effect of harmonic currents in the excitation source[J].Transactions of China Electrotechnical Society, 2003, 18(1): 5-9.

[3] 孙津济, 房建成, 王建民. 异步电动机软起动过程中的振荡[J]. 电工技术学报, 2007, 22(2):15-21.

SUN Jinji, FANG Jiancheng, WANG Jianmin.Oscillation in soft-starting of induction motor[J]. Transactions of China Electrotechnical Society, 2007, 22(2): 15-21．

[4] 赵凯岐, 王毅, 徐殿国,等. 晶闸管控制的感应电机中提高起动电磁转矩的一种新策略[J]. 中国电机工程学报, 2004, 24(3):145-150.

ZHAO Kaiqi, WANG Yi, XU Dianguo, et al. A new strategy to improve electromagnetic starting induction motors[J].Proceedings of the CSEE, 2004, 24(3):145-150.

[5] 周封, 曹俊雷, 刘健,等. 电动机离散变频软起动分频及最优切换相位控制[J]. 电机与控制学报, 2016,20(3): 13-20.

ZHOU Feng, CAO Junlei, LIU Jian,et al.Optimal switching phase and frequency splitting strategy of discretefrequency conversion soft starting control for asynchronous motor[J].Electric Machines and Control, 2016,20(3): 13-20.

[6] 王兆安，刘进军.电力电子技术[M].机械工业出版社,2009：162-169.

[7] 孟彦京, 张陈斌, 陈君,等. 一种基于正弦波电压空间矢量的新型软起动器[J]. 电力电子技术, 2014, 48(7):28-31.

MENG Yanjing, ZHANG Chenbin, CHEN Jun,et al. A novel soft starter based on sine wave voltage space vector[J].Power Electronics, 2014,48(7):28-31.

[8] 洪乃刚. 电力电子和电力拖动控制系统的MATLAB仿真[M]. 机械工业出版社,2010：139-146.

[9] 胡红明, 毛承雄, 陆继明,等. 分级交-交变频高转矩软启动器原理和仿真[J]. 电气传动, 2009, 39(2):16-19.

HU Hongming, MAO Chenxiong, LU Jiming,et al.Discrete frequency principle and simulation of high torque soft starter[J]. Electric Drive, 2009, 39(2):16-19．

[10] 童军, 张臻, 郭昌永. 电动机软启动功率因数角闭环控制技术研究[J]. 电机与控制学报, 2013, 17(12):51-56.

TONG Jun, ZHANG Zhen, GUO Changyong. Study of power factor angle closed-loop control technology in soft-starter[J]. Electric Machines and Control,2013,17(12):51-56.

(编辑：张 楠)

Research and design of discrete frequency soft starter based on equivalent sine wave principle

TONG Jun1， QIAO Jiang1， GUO Chang-yong2， LIU Li-juan1， ZHU Li-peng1

(1.College of Electrical and Control Engineering, Xi′an University of Science and Technology, Xi′an 710054, China; 2. Xi′an Branch of Gan Su Rong He Mining Equipment Group, Xi′an 710043, China)

Due to the torque of traditional soft starter is low and cannot meet the starter of heavy load needs,by using discrete frequency theory and VVVF control strategy for reference,a control method of discrete frequency soft starter was put forward based on equivalent sine. This method lowers harmonic content of motor stator’s phase current and reduces torque ripple during the process of discrete frequency soft starting so as to stabilize heavy load starting.Simulation model of seven-phase equivalent sinusoidal control system testifies the reasonability of this theory. On the basis of the above, discrete frequency soft starter experimental prototype was produced. The experimental result indicates that this method improve current waveform of motor starter effectively and is consistent with simulation result.

induction motor; soft starter; discrete frequency; equivalent sine wave principle

2015-03-12

国家自然科学基金(51307137)

童 军(1962—)，男，硕士，教授，研究方向为电力电子技术及电路与系统；

乔 江(1989—)，男，硕士研究生，研究方向为电力电子电路与装置；

乔 江

10.15938/j.emc.2016.11.006

TM 343

A

1007-449X(2016)11-0040-06

郭昌永(1984—)，男，本科，工程师，研究方向为矿用防爆电气设备的研发与设计;

刘丽娟(1990—)，女，硕士研究生，研究方向为电力电子电路与装置；

朱理鹏(1990—)，男，硕士研究生，研究方向为电力电子电路与装置。