双馈电机直流并网系统无位置传感器运行策略

年珩， 吴超

(浙江大学 电气工程学院，浙江 杭州 310027)



双馈电机直流并网系统无位置传感器运行策略

年珩， 吴超

(浙江大学 电气工程学院，浙江 杭州 310027)

为精简双馈感应发电机直流并网系统结构，在采用双变流器直流并网的基础上，进一步研究双馈电机无位置传感器控制策略。针对定子电压的非正弦性，定子侧变流器和转子侧变流器通过间接气隙磁链定向控制。为降低无位置传感器运行的参数依赖性，采用基于气隙磁链的模型参考自适应控制策略。以双馈电机数学模型为基础，采用小信号的分析方法，分析了无位置传感器策略的稳定性和对双馈电机参数变化的鲁棒性。最后构建了双馈风力发电机直流并网系统实验平台，对所提控制策略的正确性与可行性进行了实验验证。

直流输电；双馈风电机组；双变流器控制；模型参考自适应；无位置传感器运行

0 引 言

随着风电技术的发展，提高电网对风能的吸纳能力和改善风机对实际电网的适应性已成为重要的研究和发展方向。相对于传统的交流并网方式，风电系统的高压直流(high voltage direct current, HVDC)并网发电运行具有可控性好、灵活度高、故障恢复快等优势，而且解决了风电场经远距离交流输电无功损耗的问题[1-3]。因此，研究风电系统高性能直流并网运行技术具有很重要的理论和实际意义。

基于双馈感应发电机(doubly-fed induction generator, DFIG)的风电系统具有有功和无功功率独立调节、变流器容量低等优点，成为风力发电领域的主流机型。在DFIG风电系统的直流并网输电研究中，主要有以下3种拓扑结构：

1)基于电压源换流器(voltage source converter, VSC)的HVDC输电拓扑结构。

DFIG风电机组通过VSC-HVDC接入直流电网的系统结构是目前DFIG直流并网广泛应用的拓扑结构[4-6]。该系统将DFIG与背靠背结构的转子励磁变流器通过三相工频升压变压器接到风电场交流电网侧VSC变流站，将交流电变为直流电进行传输。文献[4]中详细介绍了基于VSC-HVDC的DFIG风电机组并网控制技术。文献[5]研究了大规模近海风电场VSC-HVDC并网拓扑及其控制。但图1所示拓扑结构需要经过多级能量转换才能实现风机到HVDC电网的输送，而且由于多台DFIG风机同时并联运行于VSC换流站建立的交流电网，存在系统结构复杂、风机运行可靠性差等缺点[8]。

2)基于双变流器控制的DFIG直流并网拓扑结构。

为了简化VSC-HVDC复杂的拓扑结构，文献[7-8]提出了一种基于双变流器控制的DFIG直流并网拓扑，如图1所示。其中DFIG定子侧变流器(stator side converter, SSC)和转子侧变流器(rotor side converter, RSC)的直流侧直接与直流母线相连，该直流母线通过DC/DC变换器升压连接到HVDC输电线，所提出的DFIG风电机组可以多个串联或并联再与HVDC电网相连。这种DFIG直流输电并网拓扑无需多个升压变压器和滤波器，能量传输效率高，并有效简化了系统的结构和控制复杂性，具有体积小、损耗低、成本少等优点[8]。

3)基于单变流器控制的DFIG直流并网拓扑结构。

文献[9-11]提出一种基于单变流器控制的DFIG直流并网拓扑。其中DFIG定子端直接通过一个二极管整流桥连接到直流电网，转子侧为全控变流器。由于定子侧的不控整流器使得定子磁链中含有5倍和7倍基频的谐波，从而造成6倍基频的转矩脉动。文献[11]研究了谐振调节器对转矩脉动的抑制技术，但由于拓扑自身的局限性又造成定子侧输出有功功率的波动，因此DFIG的转矩和功率脉动是这种拓扑仍需解决的问题。

因此，基于双变流器控制的DFIG直流并网拓扑结构具有最为优越的直流输电性能。文献[7-8]研究了该拓扑结构下DFIG的气隙磁场定向控制策略，但磁场定向的准确实现必须实时检测电机转子的转速和位置。传统机械式位置传感器不仅存在同心度、精度易受环境影响、可靠性低等问题，而且其信号在风力发电机和变流器之间的传递往往是长距离传输，大大降低了整个风力发电系统控制的可靠性[12-20]。

为了克服机械式位置传感器带来的问题，目前已有许多针对感应电机无位置传感器控制策略的文献，例如文献[12-20]。文献[12-15]在综述感应电机无位置传感器方法基础上，研究了直接基于电机参数计算转速的开环方法和基于比例积分(proportional integral, PI)调节器的闭环方法，并研究了转速检测和闭环控制稳定性问题。文献[16-17]采用基于转子电流的模型参考自适应(model reference adaptive system，MRAS)方法实现DFIG的位置观测。文献[18]研究了一种基于气隙功率直接计算转差角的算法，可以避免计算定子磁链，但是由于采用开环方法，不利于系统的稳定性。文献[19]采用锁相环的方法获取转子位置，但是计算过程中忽略了定子漏感，会存在一个恒定的转子位置角误差。文献[20]中采用了基于定子磁链的MRAS方法检测转子的位置，并用小信号模型分析了控制方法的稳定性，以解决同步速附近转速估测以及稳定性问题。由于本文研究的基于双变流器控制的DFIG系统中定子侧电压非正弦波，本文在文献[20]的基础上做出改进，采用基于气隙磁链的MRAS方法，并同时考虑定子漏感和定转子互感参数对于转子位置估测的影响。由于本文中采用的是气隙磁链定向控制策略，可在减小估测转子位置角随电感参数变化误差的同时提高DFIG系统的稳定性。

本文研究了基于双变流器控制的DFIG直流并网拓扑结构转子侧和定子侧变频器的控制策略，通过MRAS方法获取电机转子的速度和位置以实现准确的气隙磁场定向，并采用小信号模型分析该无位置传感器控制策略的稳定性。考虑到DFIG实际运行中电感参数会发生变化，本文进一步分析了电感参数对于位置和速度估测的影响。最后通过实验结果证明所提方法的正确性。

1 系统模型与控制算法

1.1 系统控制算法概述

基于双变流器控制的DFIG高压直流并网拓扑结构如图1所示。

在图1所示的双变流器控制的DFIG直流并网输电拓扑中，DFIG定子端电压波形并不是理想的三相正弦波形，所以基于定子电压定向的矢量控制策略并不适用于上述DFIG直流并网系统的控制。

图1 基于双变流器控制的DFIG高压直流并网拓扑Fig.1 Topology of the DFIG system based on double converters control for HVDC transmission

图2为同步旋转dq坐标系下DFIG等效电路图，考虑到定子电压是PWM波而气隙磁链为正弦波，可采用气隙磁链定向控制策略能够实现DFIG励磁分量和转矩分量的解耦控制。将气隙磁链定向到d轴可以得到：

(1)

式中：ids,iqs,idr,iqr分别为定转子电流的dq轴分量；ψdm,ψqm为气隙磁链的dq轴分量；ψds,ψqs为定子dq轴磁链；ψdr,ψqr为转子dq轴磁链；edm和eqm为气隙电势的dq轴分量；ω1为同步角速度；Ls，Lr分别为定转子自感，Lm为定转子互感；im为等效励磁电流。

在定转子侧都可以提供产生气隙磁链的励磁电流，本文中由RSC产生励磁电流，以确保DFIG产生频率可调的三相正弦气隙电势，并将SSC控制为整流器输出气隙功率，RSC流过一定的转差功率。SSC和RSC共同将捕获的风能输送到直流母线，实现传统直流并网结构中风电场侧变流站的功能。下面将分别介绍RSC和SSC的控制策略。

图2 双馈电机dq坐标系等效电路图Fig.2 DFIG equivalent circuit on the dq reference frame

1.2 RSC控制策略

RSC采用间接气隙磁链定向控制策略，以输出可控的DFIG气隙电势幅值和相角。将气隙磁链定向在同步旋转dq坐标系的d轴方向，其空间位置θm可通过基准角频率ω1的积分得到。

DFIG转子电压方程可表示为：

(2)

采用气隙磁链定向后，将式(1)代入式(2)后可以得到转子电压为：

(3)

式中：Lr=Lr-Lm为转子漏感;kpr，kir为转子电流环PI调节器的比例参数和积分参数；s为拉普拉斯算子。

励磁电流的参考值通过下式计算为

(4)

转子d轴电流的参考值为励磁电流和定子d轴电流的差值，有

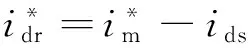
(5)

由式(1)可得，转子q轴电流参考可表示为

(6)

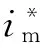
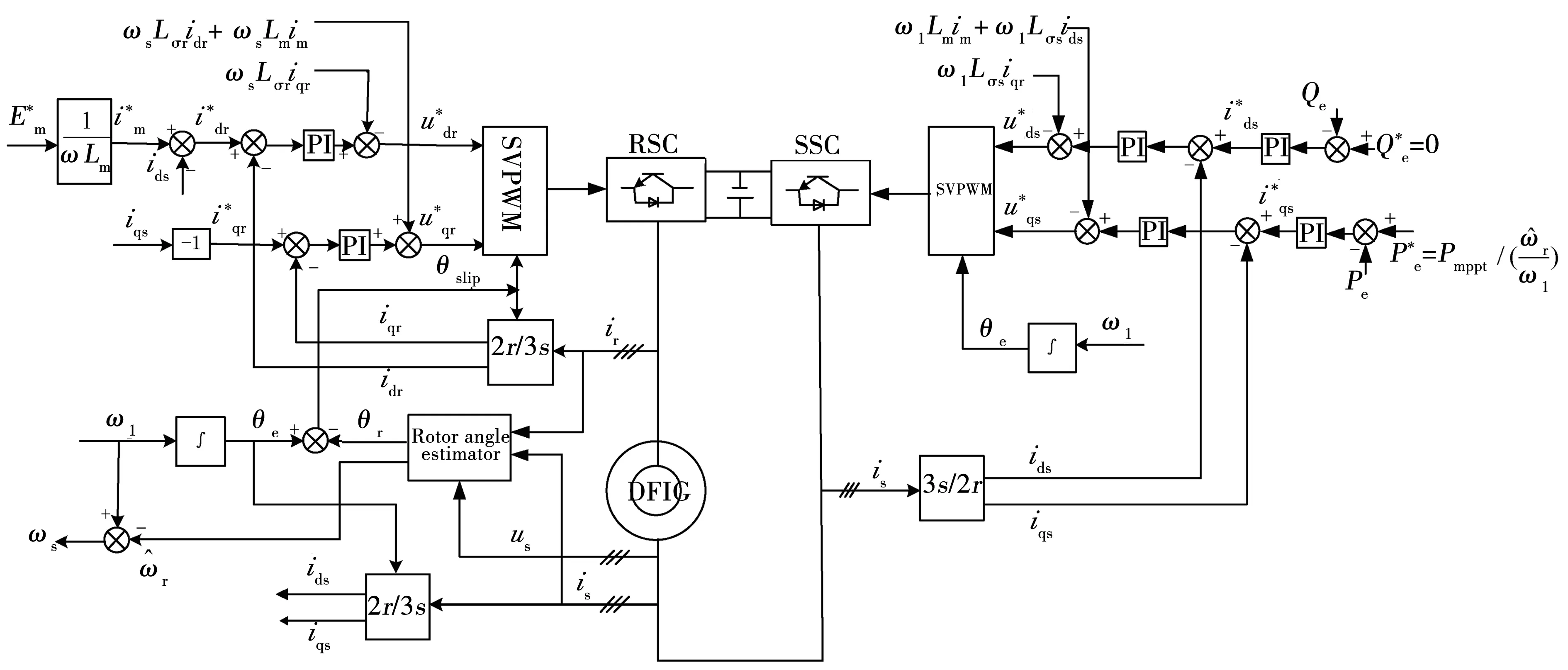
图3 定子侧变流器和转子侧变流器的控制框图Fig.3 Control scheme of SSC and RSC

1.3 SSC控制策略

通过RSC的气隙磁场定向控制，可在DFIG气隙中产生稳定的三相正弦反电势。因此，SSC可以控制为整流器实现对DFIG输出功率的控制。由于气隙磁链定向在同步旋转dq坐标系的d轴方向，且气隙反电势位于同步旋转dq坐标系的q轴，所以定子q轴电流为有功分量，定子d轴电流为无功分量。在以基准角频率ω1旋转的dq坐标系中，DFIG定子电压的方程可表示为

(7)

式中uds,uqs为定子dq轴电压。将式(7)代入式(1)可以得到DFIG定子dq轴电压参考为：

(8)

在气隙磁链定向的条件下，DFIG输出的气隙有功、无功功率可表示为：

(9)

可见在该定向条件下，DFIG输出的气隙有功、无功功率可以由定子电流的d、q轴分量独立解耦控制。根据最大风能跟踪及单位功率因数的工作原理，气隙有功和无功功率的给定值分别设定为：

(10)

式中Pmppt是最大风能曲线对应的风机功率。在不考虑定子电阻上的功率损耗后，一般可以认为DFIG输出的气隙功率也就是定子侧输出的功率，所以在后文中直接用定子功率代替气隙功率。

2 转子位置估算

2.1 模型参考自适应算法

为实现DFIG在气隙磁链定向下的无位置传感器运行，参考文献[20]采用的定子磁链作为参考的MRAS方法，本文进一步研究MRAS在双变流器控制下对DFIG转子位置的检测方法。

在静止坐标系下，采用定子电压和定子电流表示气隙磁链为

ψm=∫(us-Rsis)dt-Lσsis。

(11)

在静止坐标系中采用定子电流和转子电流表示气隙磁链为

(12)

式(11)计算的磁链作为参考磁链，式(12)计算的磁链作为自适应磁链，通过调节估测的转子速度，使得自适应磁链与参考磁链之间的误差为0，以获得准确的转子速度。磁链误差在静止αβ坐标系中可表示为

(13)

转子位置和速度估测模块结构如图4所示，其中磁链误差作为PI调节器输入，PI的输出即为估测的转速，通过积分后获得转子位置估测值以实现DFIG的无位置传感器运行。

图4 转子位置估测的MRAS模块Fig.4 MRAS observer for rotor angle estimating

2.2 小信号模型

为分析DFIG采用MRAS实现无位置传感器运行的稳定性，本文进一步建立气隙磁链定向下的小信号模型。为便于对图4中MRAS模型进行小信号建模，可将气隙磁链误差在同步旋转dq坐标系下表示为

(14)

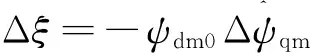
(15)

在同步坐标系中采用电流模型的气隙磁链表达式为

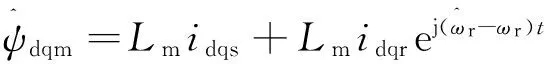
(16)

(17)

(18)

假如稳态时θerror0=0，则可得到如下关系式：

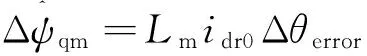
(19)

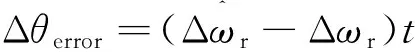
(20)

将式(15)～式(21)从时域归算到s域，可以得到转速波动过程小信号模型的传递函数如图5所示。

图5 小信号模型框图Fig.5 Scheme of small signal model

根据图5所示的小信号模型的闭环框图，可以得到其开环传递函数为

(21)

根据小信号模型的开环传递函数可以绘制出其开环传递函数的根轨迹如图6所示。传递函数的两个极点都在原点(图中叉号表示)，有一个小于零的零点(图中小圆圈表示)，根据根轨迹的绘制原则，从极点出发，收敛于零点或者无穷远，且关于实轴对称，可以得到图6所示的根轨迹。根轨迹全部在左半平面。因此，当实际转速发生波动时，估测转速也能够稳定的跟踪上实际转速。

图6 小信号模型的根轨迹Fig.6 Sketch of root locus for small signal model

2.3 电机参数影响

在上述的MRAS算法中，需要用到定子电阻、定子漏感、定转子互感这些电机参数，所以这些电机参数的准确性对估测的转子位置精度有一定的影响。由于定子电阻很小，所以电阻参数的影响可以忽略不计。如果电机在运行时电感参数有一定的变化，而在图4的模型中没有及时的改变电感参数值，那么计算出的转子位置角将有一定的误差。下面将讨论互感和定子漏感参数的变化对转子位置角的影响。

当定子漏感参数和互感参数与实际值不相等时，由图4中的模型可以看出气隙磁链存在两个误差。第一个是由于定子漏感不对造成参考气隙磁链的误差，第二个误差是由于定转子互感不对造成估测气隙磁链的误差，这两个误差之和是气隙磁链的总误差，也就是估测转子位置角的误差。

对于第一个误差，当定子漏感实际值与图4模型中的定子漏感值不一样时，通过电压模型计算的气隙磁链不是准确值，但是通过电压模型计算的定子磁链还是准确的，所以可通过定子磁链表示出气隙磁链，然后计算气隙磁链的误差。

采用定子磁链和定子电流表示气隙磁链为

ψm=ψs-Lσsis。

(22)

将上式写成同步坐标系dq轴分量的形式为

(23)

气隙磁链在同步坐标系中的位置角θ1为

(24)

(25)

气隙磁链的误差角为

(26)

实际中一般控制定子无功功率为0，则定子d轴电流为0。所以式(26)可以化简为

(27)

对于第2个误差，气隙磁链采用定子电流和转子电流表示时，在同步坐标系中的位置角为

(28)

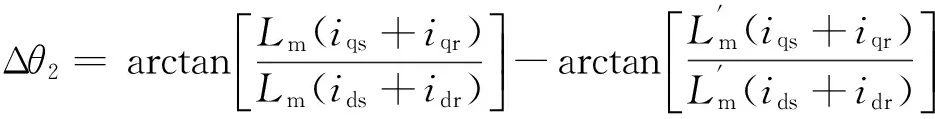
(29)

第2个误差是由于互感参数变化引起的，但是由于在本文中采用的是气隙磁链定向控制策略，定子q轴电流和转子q轴电流之和为0，所以不管定子互感如何变化，式(29)计算的误差角一直为0，所以通过电流模型计算的转子位置角度能准确的跟踪电压模型计算的气隙磁链位置角。因此，在气隙磁场定向控制策略下，由于互感参数变化引起的位置观测误差是不存在的。转子估测位置误差仅仅是由定子漏感参数变化引起的。

由式(27)可以看出，转子误差角不光与定子漏感相关，还与转矩电流iqs和定子磁链相关。但是在控制中定子磁链一般维持在额定值，所以可以认为是恒定值。但是iqs是随着定子输出有功功率不同而变化的，即电机在不同的输出功率下，估测的位置角误差也会有变化。由于电机电感参数通常的变化范围为±20%，为表示转子位置误差角与电机定子漏感参数和转矩电流的关系，在Matlab/SIMULINK中分析了定子漏感参数变化±20%时，DFIG运行在额定频率和额定磁链(DFIG参数见表1)，DFIG定子输出功率分别为500 W、750 W、1 000 W时的转子估测位置角的误差。

由于定子漏感很小，而且在气隙磁链定向的情况下，定子磁链q轴分量很小，此时的反正切基本为线性关系，所以图7中的误差曲线基本呈现线性关系。而且从图中还可以看出，定子漏感参数在同样的变化下，定子输出功率越大，误差越大。当输出功率为1 000 W时，最大的转子位置误差角为1.3°，仍可满足DFIG矢量控制的运行要求。

图7 电感参数变化20%的转子位置角误差Fig.7 Rotor angle error with inductance varying twenty percent

3 实验验证

为了验证上文中所提出的基于双变流器控制的DFIG无位置传感器运行技术的可行性和有效性，构建了DFIG并接直流电网的模拟装置，实验平台系统框图如图8所示。其中采用变频器拖动的鼠笼式异步电机模拟风力机，并与DFIG同轴相连。由于在HVDC系统中，高压直流母线的电压由远端大电网侧的变流站控制恒定，因此在实验装置中，用一个直流源来模拟直流电网。表1给出了实验中使用的DFIG电机参数，并网控制算法的实现基于TI公司的DSP TMS320F28335，采样频率为10 kHz，IGBT开关频率设定为10 kHz。实验波形由横河YOKOGAWA的DL750录波仪采集。

表1 实验系统参数

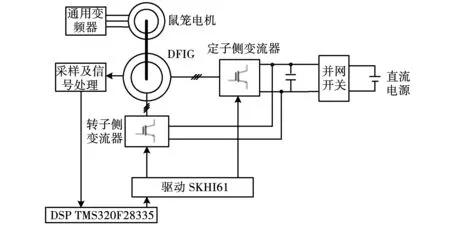
图8 实验平台系统框图Fig.8 Schematic diagram of the experiment system

图9为DFIG定子侧输出功率为500 W时的稳态波形图。因为电机的额定电压为110 V，当定子输出功率500 W时，定子相电流峰值为3.7 A，THD为5.45%。转子电流相电流峰值为1.44 A，THD为3.97%。其中实际转子位置和估测的转子位置存在0.05°的位置误差，这可能是由于DSP的采样和控制时延导致，由于该误差角很小，对于气隙磁场定向的控制效果基本没有影响。

为了验证无位置传感器控制方法在功率给定变化和转速变化时的动态性能，给出了图10和图11的实验波形。

图10是定子有功功率从250 W变化到750 W的波形图。控制DFIG定子输出功率给定在图中所示t1时刻从250 W线性升高，在1.4 s后即t2时刻稳定在750 W。从图中可以看出，定子电流、转子电流、电磁转矩均能跟随给定值平滑增加，定子相电流幅值从1.85 A变化到5.5 A，转子实际相电流幅值从0.97 A变化到2 A。在给定功率变化过程中，实际转子位置角和估测转子位置角的误差保持在0.05°以内，估测转速与实际转速基本相同，估测的转子位置角在功率变化过程中也具有很好的跟随性。

图9 定子输出功率500 W的实验结果Fig.9 Experiment result of DFIG with stator output power being 500 W

图10 定子输出功率从250 W到750 W实验结果Fig.10 Experiment result of DFIG with stator output power changing from 250 W to 750 W

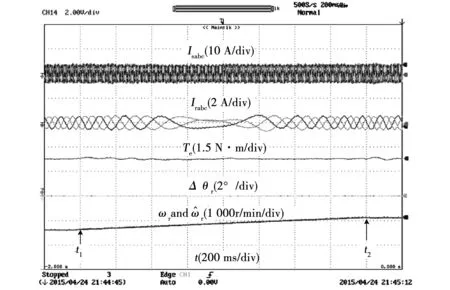
图11 转速从次同步到超同步变化实验结果Fig.11 Experiment result of DFIG with rotor speed changing from sub-synchronous to super-synchronous state

图11是转子转速从次同步(800 r/min)变化到超同步(1 200 r/min)的动态过程波形图。DFIG转速在图中所示t1时刻从800 r/min线性升高，在1.6 s后即t2时刻稳定在1 200 r/min。从图中可以看出，定子电流基本没有变化，转子电流频率从10 Hz变到0然后又变到10 Hz，估测转速波形与实际转速变化波形重合，这表明估测转速具有很好的跟随性。而且由转子位置误差角的波形可以看出在转速动态变化过程中，位置误差稳定在0.05°以内，所以无位置传感器算法在转速变化时也具有很好的跟随性和很小的超调量。

图12为定子输出500 W功率时，互感和定子漏感均有正向20%误差时的DFIG实验波形。可以看出，此时转子估测位置与实际位置会存在0.8°的检测误差，这与前面的理论分析和分析结果图9是一致的。图中的定子电流THD为6.72%，转子电流THD为4.68%，相比较于图11中的波形可以发现，定转子电流的THD都有一定的增大，但是DFIG仍可正常运行，表明本文研究的无位置传感器控制方法对于电感参数的变化不敏感，具有较高的鲁棒性。

图12 电感参数有20%误差的实验结果Fig.12 Experiment result of DFIG with inductance varying twenty percent

4 结 论

本文研究了一种基于双变流器控制的DFIG无位置传感器运行技术。采用基于气隙磁链的MRAS方法估算转子位置并实现DFIG的直流并网发电运行，通过小信号模型验证了DFIG无位置传感器运行的稳定性。分析发现，所提无位置传感器控制策略的位置检测精度不受互感参数变化的影响，在20%漏感参数变化范围内，估测的转子位置和速度仍具有较高的精度，DFIG系统具有较好的发电运行性能。

[1] 汤广福，罗湘，魏晓光. 多端直流输电与直流电网技术[J].电机工程学报，2013，33(10)：8-17.

TANG Guangfu，LUO Xiang，WEI Xiaoguang. Muli-terminal HVDC and DC-grid Technology[J]. Proceedings of the CSEE，2013，33(10)：8-17.

[2] 张文亮，汤涌，曾南超. 多端高压直流输电技术及应用前景[J]．电网技术，2010，34(9)：1-6．

ZHANG Wenliang，TANG Yong，ZENG Nanchao. Multi-terminal HVDC transmission technologies and its application protects in China[J]. Power System Technology， 2010， 34(9)： 1-6．

[3] 王常骐，郭家虎. 风电场直流并网的拓扑结构研究[J]. 电网技术，2014，38(11)：3065-3070.

WANG Changqi, GUO Jiahu. Research on topological structures for DC grid-connection of wind farm[J]. Power System Technology,2014，38(11)：3065-3070.

[4] 李文津，汤广福，康勇，等. 基于VSC-HVDC的双馈式变速恒频风电机组启动及并网控制[J]. 中国电机工程学报，2014，34(12)：1864-1873.

LI Wenjin，TANG Guangfu，KANG Yong，et al. Starting up and integration control of doubly-fed variable-speed constant-frequency wind power generator based on VSC-HVDC[J]. Proceedings of the CSEE，2014，34(12)：1864-1873.

[5] 朱晓东，周克亮，程明，等. 大规模近海风电场VSC-HVDC并网拓扑及其控制[J]. 电网技术，2009，33(18)：17-24.

ZHU Xiaodong，ZHOU Keliang，CHENG Ming，et al. Topologies and control of VSC-HVDC Systems for Grid-connection of large-scale offshore wind farm[J]. Power System Technology， 2009，33(18)：17-24.

[6] YAO Xingjia, SUI Hongxia, XING Zuoxia. The study of VSC-HVDC transmission system for offshore wind power farm[C]//International Conference on Electrical Machines (ICEMS), October 8-11, 2007, Seoul, Korea. 2007:314-319.

[7] PODDAR G，RANGANATHAN V T. Sensorless double-inverter-fed wound-rotor induction-machine drive[J]. IEEE Transactions on Industrial Electronics，2006，53(1)：86-95.

[8] 年珩，易曦露.面向直流输电的双馈风电机组并网拓扑及控制技术[J].电网技术，2014,38(7):1731-1738.

NIAN Heng，YI Xilu. HVDC power transmission oriented grid-connection topology and control strategy for wind farm composed of doubly fed induction generators[J]. Power System Technology，2014，38(7): 1731-1738.

[9] MARQUES G D,IACCHETTI M F. Stator frequency regulation in a field oriented controlled DFIG connected to a DC Link[J]. IEEE Transactions on Industrial Electronics，2014，61(11)：5930-5939.

[10] IACCHETTI M F，MARQUES G D. A scheme for the power control in a DFIG connected to a DC-Bus via a diode rectifier[J]. IEEE Transaction on Power Electronics，2015，30(3)：1286-1296.

[11] IACCHETTI M F,MARQUES G D. Torque ripple reduction in a DFIG-DC system by resonant current controllers[J]. IEEE Transactions on Power Electronics，2015，30(8)：4244-4254.

[12] 邹旭东，康勇，陈坚.感应电机矢量控制系统无位置传感器控制方案研究[J].电气传动,2004,34(4):3-7.

ZOU Xudong，KANG Yong，CHEN Jian. Study on speed sensorless schemes of induction motor vector control system[J]. Electric Drive，2004，34(4)：3-7.

[13] 陈伯时，杨耕. 无位置传感器高性能交流调速控制的三条思路及其发展建议[J].电气传动，2006，36(1):3-8.

CHEN Boshi，YANG Geng. Three approaches to the control strategies of sensorless high-performance ASD systems and proposals for their development[J]. Electric Drive，2006，36(1)：3-8.

[14] 苑国锋，李永东，柴建云. 双馈异步风力发电机新型无位置传感器控制方法[J]. 清华大学学报(自然科学版)，2009，49(4)：461-464.

YUAN Guofeng，LI Yongdong，CHAI Jianyun. Positioning sensorless control method for doubly fed induction wind power generator[J]. Journal of Tsinghua University(Science and Technology)，2009，49(4)：461-464.

[15] 阎耀明，范瑜. 无位置传感器的双馈电机在风力发电系统中应用研究[J].太阳能学报，2003,24(3):432-436.

YAN Yaomin，FAN Yu，WANG Zhizhong. Research on speed sensorless control of doubly fed induction machine for wind-energy generation[J]. Acta Energiae Solaries Sinica，2003,24(3):432-436.

[16] 马小亮，刘志强. 基于电流辨识速度的双馈矢量调速系统的研究[J].电工技术学报，2003,18(4):83-93.

MA Xiaoliang，LIU Zhiqiang. Study on doubly-fed vector speed regulating system with speed identification based on current[J]. Transactions of China Electrotechnical Society，2003，18(4)：83-93.

[17] 刘志强，王娜. 无位置传感器转子电流定向双馈电机的矢量控制调速系统[J].中小型电机,2002，29(6):38-42.

LIU Zhiqiang，WANG Na. Speed variable vector control system of doubly fed motor without speed sensor based on rotor current oriented[J]. S&M Electric Machines，2002，29(6)：38-42.

[18] MARQUES G D，SOUSA D M，IACCHETTI M F. Air-gap power-based sensorless control in a DFIG connected to a DC link[J]. IEEE Transaction on Energy Conversion，2015，30(1)：367-375.

[19] SHEN Baike，MWINYIWIWA Bakari，ZHANG Yongzheng. Sensorless maximum power point tracking of wind by DFIG using rotor position phase lock loop(PLL)[J]. IEEE Transaction on Power Electronics，2009，24(4)：942-951.

[20] ROBERTO Cárdenas，RUBÉN Pea.MRAS observer for sensorless control of standalone doubly fed induction generators[J]. IEEE Transaction on Energy Conversion，2005，20(4)：710-718.

(编辑：刘琳琳)

Sensorless control strategy of doubly-fed induction generator connected to DC grid

NIAN Heng， WU Chao

(College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China)

In order to simplify the complexity of doubly-fed induction generator (DFIG) system connected to DC grid, the sensorless operation technique is further studied on the basis of two converters. Aiming at that stator voltage is not sinusoidal, the stator side converter and the rotor side converter was controlled through the indirectly air-gap flux orientation. In order to reduce the dependency on the parameters, the model reference adaptive system based on air-gap flux was applied to achieve the sensorless operation. The small signal method was applied to analyze the stability of the sensorless operation and the robustness against the DFIG parameter variations on the basis of mathematical model of DFIG. Finally, the experimental system of DFIG connected to DC grid is developed to validate the sensorless operation technique.

DC power transmission；doubly-fed induction generator；dual converters control; model reference adaptive system; sensorless operation

2015-06-25

国家自然科学基金(51277159)

年 珩(1978—),男,博士,教授，博士生导师,研究方向为新能源技术、风力发电技术等;

吴 超(1992—),男,博士研究生，研究方向为双馈电机直流并网新型拓扑结构与控制策略研究。

年 珩

10.15938/j.emc.2016.11.001

TP 46;TM 315

A

1007-449X(2016)11-0001-09