带自适应估计器的微电网逆变器跟踪控制

闫士杰， 闫伟航， 高文忠

(1.东北大学 信息科学与工程学院，辽宁 沈阳 110819； 2.丹佛大学 电气和计算机工程系，美国 丹佛 80208)



带自适应估计器的微电网逆变器跟踪控制

闫士杰1， 闫伟航2， 高文忠2

(1.东北大学 信息科学与工程学院，辽宁 沈阳 110819； 2.丹佛大学 电气和计算机工程系，美国 丹佛 80208)

针对电压型微电网逆变器接入本地非线性负载产生输出电压波形畸变问题，提出一种基于自适应估计器的微电网逆变器跟踪控制策略。在该控制策略中，构造一个自适应估计器，用它来估算出因各种扰动产生的微电网逆变器电压降，并进行前馈补偿，求出逆变器的电压控制矢量。为了实现对微电网电压的实时跟踪，引入虚拟阻抗概念，将谐波压降、滤波器电感和电阻参数变化以及各种外部扰动等产生的压降等效成虚拟阻抗上产生的压降。以此为基础，估算出相关的等效虚拟阻抗，并修改自适应估计器中的参数，提高逆变器输出电压波形质量。在各种负载条件下进行了仿真和实验，取得了良好的控制效果。

微电网逆变器；自适应估计器；虚拟阻抗；非线性负载；跟踪控制

0 引 言

微电网逆变器是一种可再生能源与微电网之间的功率接口装置，广泛应用于新能源发电系统中。特别是太阳能发电、小型风力发电等分布式发电系统的大量使用，使得人们对作为微电网逆变器提出了更高的要求[1-5]。在微电网中，对于任何负载，逆变器不论在独立工作模式下，还是在并网工作模式下，保持输出电压波形正弦都是非常重要的[6-7]。在传统的电压型逆变器中，常见的控制方法大多以电压的幅值，或有效值等直流量控制为主，不控制相位。当微电网中接入非线性负载，或者逆变器带本地非线性负载时和直流侧电压波动时，微电网逆变器输出电压就会产生波动，从而使逆变器输出电压波形不能快速跟踪微电网设定的波形，存在幅值和相角误差，导致微电网中电压波动。为了改善微电网逆变器的输出性能，一些适用于快速系统瞬时跟踪和控制的先进控制理论，如无差拍控制[8]、重复控制[9-10]、状态观测器反馈控制[11-12]和H∞控制[13]等已应用到逆变器控制系统中。无差拍控制方法能够进行瞬时电压控制，完成轨迹跟踪功能，输出电压谐波畸变率小。但是无差拍控制要求精确的数学模型，对控制对象参数的依赖性很强。当逆变器所带负载突然增大，或者带非线性负载时，输出滤波器中的参数会因谐波和温度而发生变化，导致控制效果明显变差。重复控制方法能够实现很好的轨迹跟踪功能，广泛应用于电力电子系统中。但是重复控制是基于内模原理的一种控制方法，控制精度取决于内部模型是否能够很好地描述系统外部特性。由于延迟因子的存在，重复控制得到的控制指令并不是立即输出，而是滞后一个参考周期才会输出，因此重复控制对于位置等慢变化轨迹有很好的跟踪效果。但对正弦电压和电流等快变化轨迹的跟踪，要想取得良好的控制效果，必须应用高性能硬件资源，大幅提高采样频率和控制频率。状态观测器是一种能够根据输出量来重构系统状态的方法，广泛应用于电力变换系统中。应用状态观测器进行系统控制时，一般借助先进控制理论来实现，对逆变器硬件资源要求较高。H∞控制是一种优化控制，主要通过扰动补偿和系统性能优化来实现，但要求计算量大。除此之外，还有带谐振控制器控制[14-15]、智能控制[16-17]、预测控制[18-19]、波形控制[20]等。

虚拟阻抗控制是近年来提出的一种基于阻抗变换的逆变器控制方法，在三相逆变器并联控制中获得了广泛应用，能够很好解决微型电网中多逆变器负载电流的精确分配问题[21-22]。为此，本文提出一种微电网逆变器跟踪控制方法。该方法基于自适应估计器，结合虚拟阻抗设计，对逆变器输出产生的电压降实现快速前馈补偿，从而实现对微电网设定电压波形的快速跟踪。该控制方法简单，波形跟踪效果好，且不需要高性能硬件资源。最后利用DSP和FPGA相结合，在逆变器带纯电阻负载和二极管串联的情况下，进行了仿真和实验研究。

1 带虚拟阻抗的逆变器等效电路

本文研究的微电网逆变器是电压型单相逆变器，主电路如图1所示。在图1中，T1～T4为逆变器的功率开关管；Ud为逆变器直流侧电压；L为逆变器滤波电感，取值4.5 mH；R为电感内阻，取值1.2；C为滤波电容，取值40F；uAB为逆变器桥臂间电压；i为逆变器输出电流；uOUT为负载电压；i0为负载电流。本地负载Z0可以是线性负载，也可以是非线性负载。

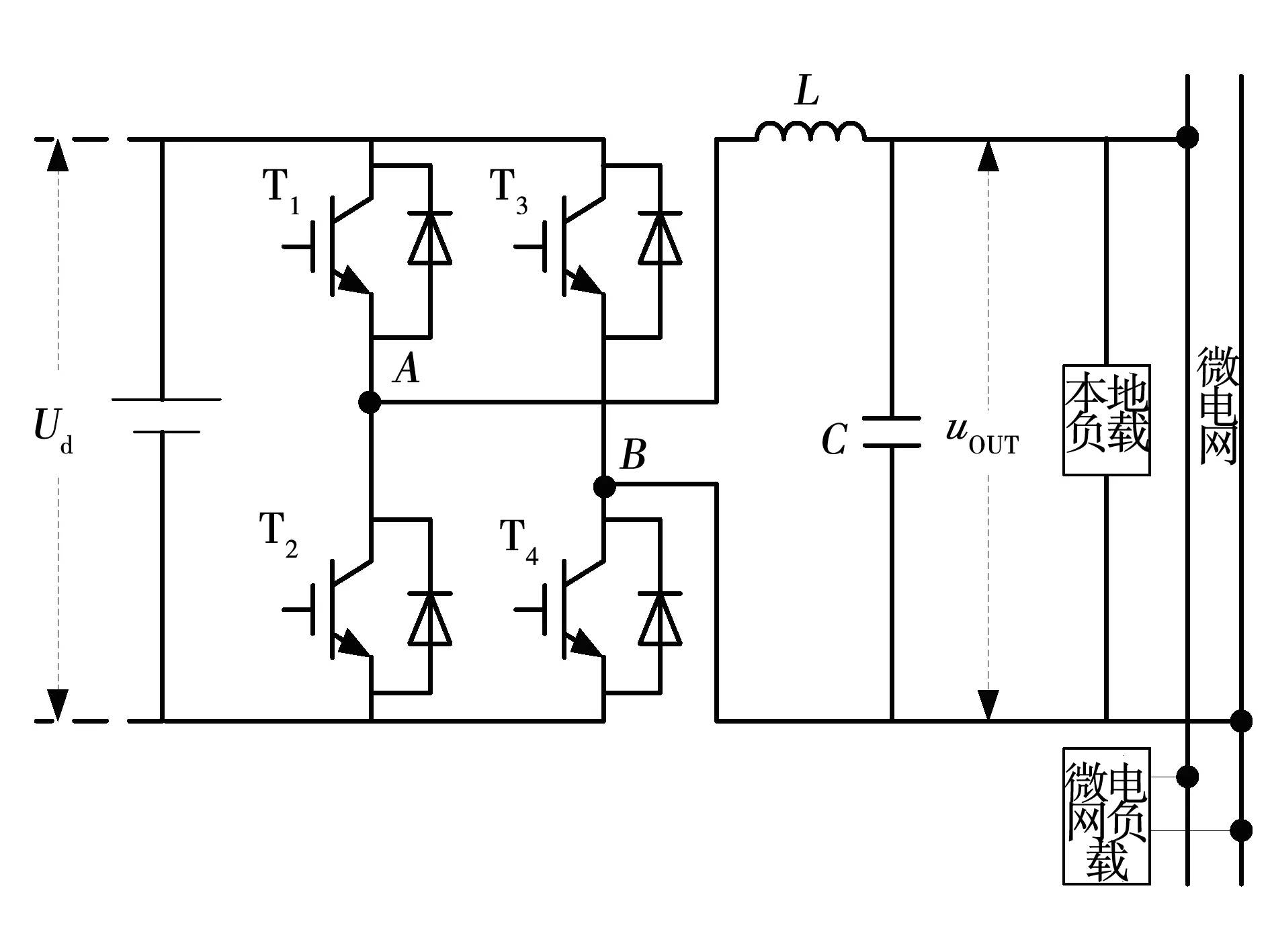
图1 微电网逆变器主电路Fig.1 Main circuit of microgrid inverter

根据图1，可画出微电网逆变器主电路的等效电路，如图2所示。

假设本地负载Z0由逆变器供电，同时向微电网输入电能，则根据基尔霍夫定律(Kirchoff's law)，写出微电网逆变器回路方程为

(1)

图2 微电网逆变器等效电路图Fig.2 Equivalent circuit diagram of microgrid inverter

当逆变器负载增加时，由于滤波器电感及其内阻压降影响，逆变器输出电压会因滤波器压降而降低。采用电压闭环调节后，幅值可调至给定幅值，但相位可能出现滞后。当逆变器带非线性负载时，由于总电流中含有谐波电流，导致逆变器输出电压的变化更大，并且不能通过电压闭环调节至给定值。假设滤波器参数恒定。当负载变化时，逆变器输出电流变化量为Δi，则式(1)可变换为

(2)

定义滤波器电阻上的压降为有功压降ΔuD，滤波器电抗上的压降为无功压降ΔuQ，则有：

(3)

将式(3)代入式(2)中，可得

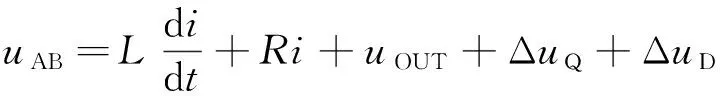
( 4)

考虑一般情况，可以将逆变器因所有扰动(包括谐波和PWM调制等影响)而引起的逆变器输出电压uOUT变化都统一等效为式(3)所示的有功压降和无功压降。如图3所示。

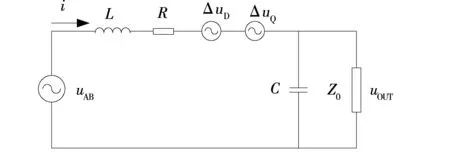
图3 电压波动时的等效电路图Fig.3 Equivalent circuit diagram with voltage fluctuation

在电气控制系统中，有功压降通常定义为电阻上的压降，无功压降通常定义为电感上的压降。在图3中，假设负载电流有效值不变，将有功压降和无功压降分别定义为虚拟电阻R*和虚拟电感L*上的压降，则有：

(5)

将式(5)代入式(4)得

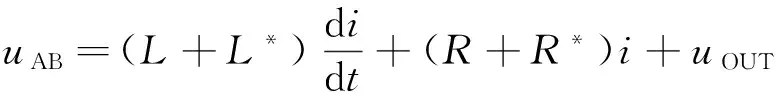
(6)

由此可以得出结论：因外部干扰等因素而导致逆变器输出电压变化时，就会存在等效的虚拟阻抗。带虚拟阻抗的等效电路如图4所示。

图4 带虚拟阻抗的等效电路图Fig.4 Equivalent circuit diagram with virtual impedance

针对图4，应用虚拟阻抗估计器计算出虚拟电感L*和虚拟电阻R*，推导出有功压降ΔuD和无功压降ΔuQ，然后补偿到电压控制回路，就可保持输出电压与给定电压相同。系统框图如图5所示。

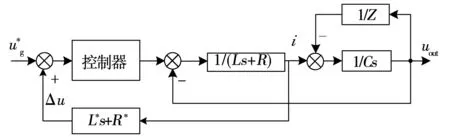
图5 带虚拟阻抗的系统框图Fig.5 Block diagram of system withvirtual impedance

从图6可以看出，无论R*或者L*如何变化，系统的特征根均位于虚轴的左侧，即系统是稳定的。

系统控制目标：应用虚拟阻抗，修改控制器中的参数，在直流侧电压波动、负载突变和非线性负载接入等情况下使逆变器的输出电压uOUT实时跟踪微电网给定的正弦电压波形，保证逆变器输出电压总谐波畸变率THD(total harmonic distortion)最小。

图6 开环传递函数的根轨迹簇Fig.6 Root locus cluster of open loop transfer function

2 自适应估计器的构成

微电网逆变器运行过程中，由于带非线性负载时会产生谐波电流，所以压降ΔuD和ΔuQ主要由负载电流i0产生的。设u为逆变器的输出电压控制矢量，则对于双极性调制时，式(6)可写成：

(7)

(8)

设计自适应估计器，则逆变器输出电压控制矢量具有形式

(9)

(10)

(11)

虚构一个相互垂直的DQ坐标系为参考，则e和i0的第k次谐波分量幅值为：

(12)

(13)

当逆变器输出负载电流为i0，产生电压降e后，则第k次谐波消耗的等效有功功率和无功功率为：

(14)

(15)

从上面的分析可以看出，只要逆变器输出不是给定的正弦波形，在基波中除了正弦波压降外，还会产生非正弦波压降。从而通过式(15)，就能够估算出回路中第k次谐波虚拟阻抗参数。本论文中，只讨论有限次谐波，即k取1、3、5、7、9、11。

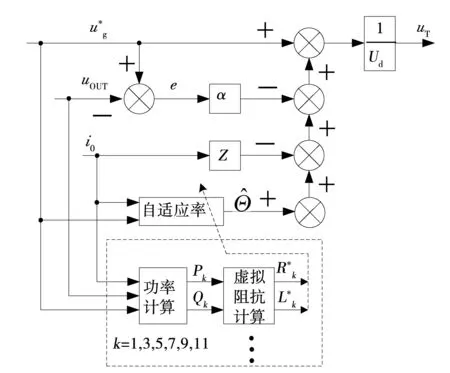
图7 自适应估计器框图Fig.7 Block diagram of adaptive estimator

3 仿真结果及分析

图8为在线性负载条件下，不加入自适应估计器，仅采用比例控制时的逆变器输出电压波形和跟踪偏差。图9为在图8基础上，加入自适应估计器时的逆变器输出电压波形和跟踪偏差。图10为自适应估计器前馈补偿信号。

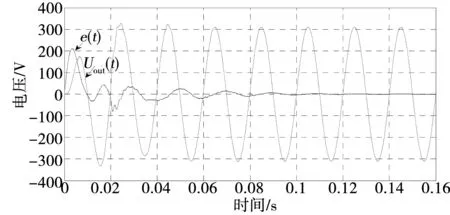
图8 线性负载时不带自适应估计器的输出电压和跟踪偏差Fig.8 Output voltage and error without adaptive estimator in linear load

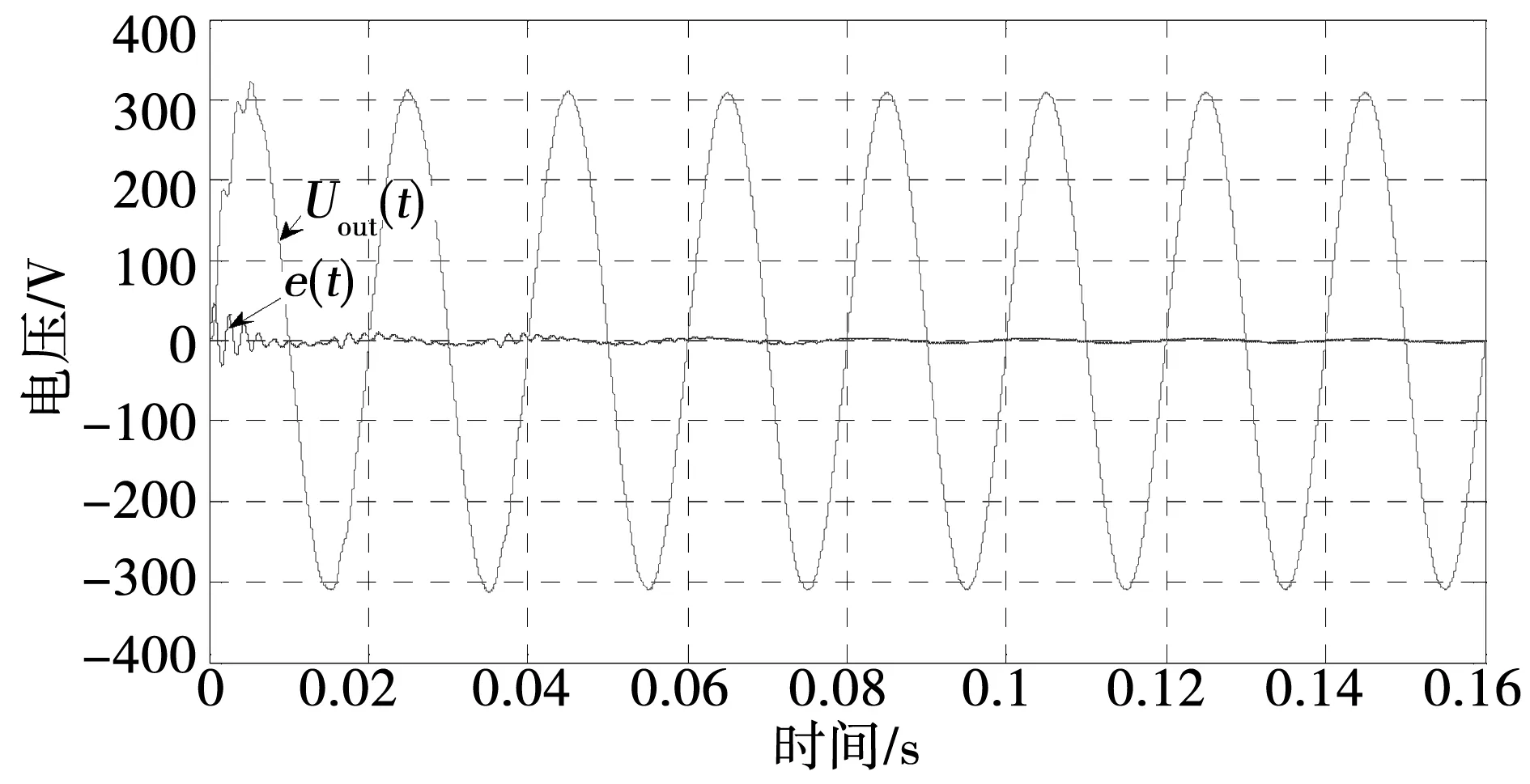
图9 线性负载时带自适应估计器的输出电压和跟踪偏差Fig.9 Output voltage and error with adaptive estimator in linear load

比较图8和图9，在不带自适应估计器的情况下，跟踪偏差e变化比较大，逆变器输出电压经过4个周期才能完好跟踪给定电压。在带自适应估计器的情况下，跟踪偏差e变化明显变小，逆变器输出电压经过2个周期就能完好跟踪给定电压。图10表示了加入自适应估计器后输出的补偿量波形。系统运行前期，由于输出与给定信号偏差较大，故跟踪控制器的前馈补偿量较大，随着系统的稳定，其输出的补偿量逐渐减小，最后趋于稳定。这说明逆变器输出电压波形能够很好跟踪微电网给定电压波形。

图10 自适应估计器的前馈补偿信号Fig.10 Feed-forward compensation signal of adaptive estimator

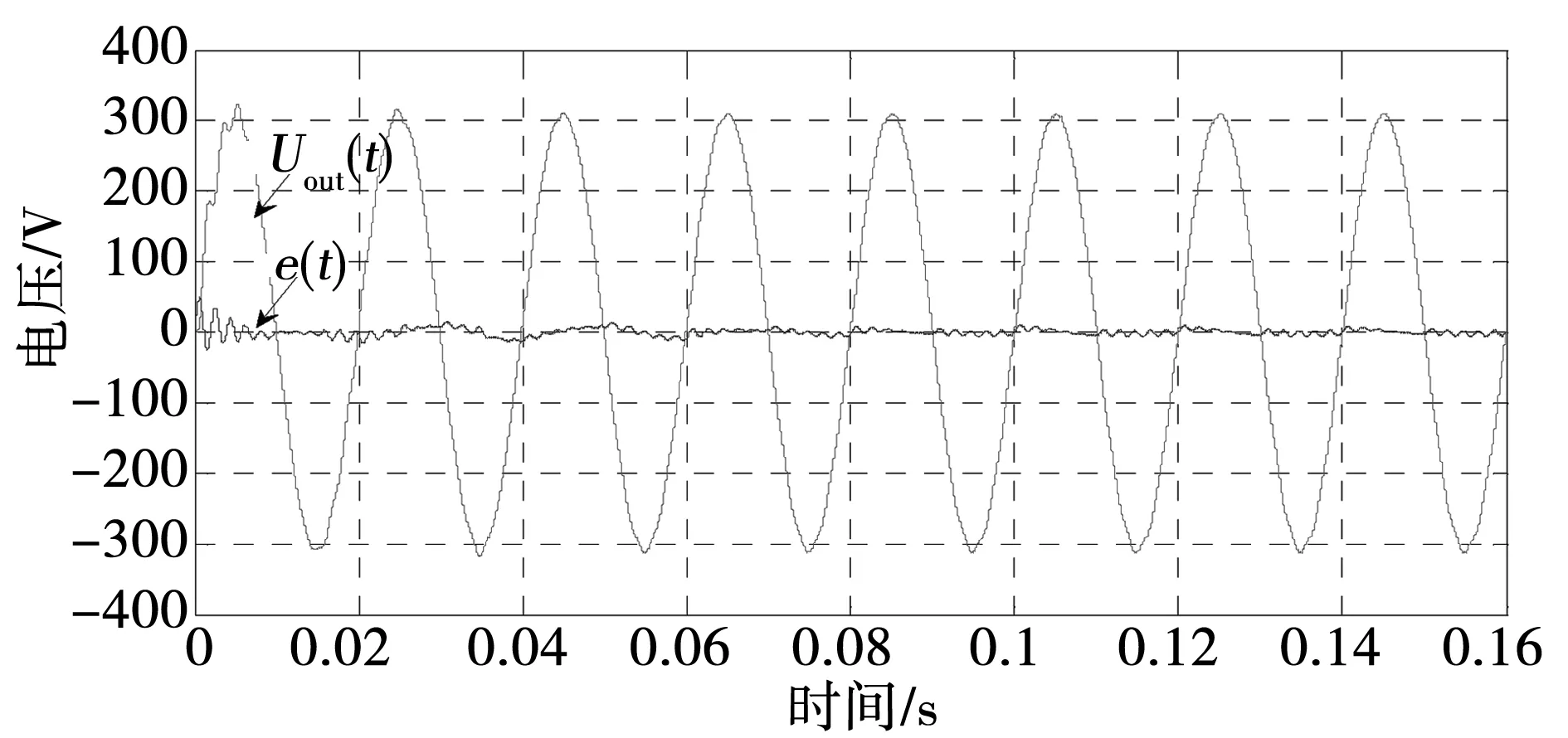
图11 非线性负载时带自适应估计器的输出电压和跟踪偏差Fig.11 Output voltage and error with adaptive estimator in nonlinear load

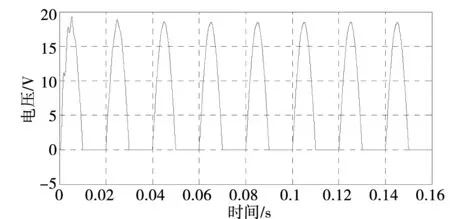
图12 非线性负载时带自适应估计器的输出电流Fig.12 Output current with adaptive estimator in nonlinear load

为了验证本控制系统在非线性负载条件下的电压跟踪能力，将电阻和二极管串联，形成非线性负载。图11为加入自适应估计器时的逆变器输出电压波形和跟踪偏差。图12为非线性负载的电流波形。比较图9和图11可以看出，逆变器带非线性负载时，跟踪偏差e变化略有增大，逆变器输出电压经过3个周期也能完好跟踪给定电压。

4 实验结果及分析

本系统采用DSP TMS320F2812A与FPGA XC3S250E相结合进行实验。在DSP中，完成采样和通讯，在FPGA中实现自适应估计器模块、跟踪控制器模块和PWM波形生成模块。实验时主电路参数和控制电路参数与仿真时相同，以微电网电压波形作为给定电压波形。实验波形如图13～16所示。为了便于区分，将逆变器输出电压波形按照电网电压波形的2倍衰减。

图13为逆变器带电阻负载时的输出波形。从图13中可以看出，逆变器输出电压波形经过2个周期后，能够很好跟踪上微电网电压波形。图14为稳态时的输出电压谐波畸变率，THD仅为2.6%。

图13 线性负载时带自适应估计器的输出电压Fig.13 Output voltage with adaptive estimator in linear load

图14 带自适应估计器的输出电压谐波表Fig.14 Harmonics table of output voltage with adaptive estimator

图15为突加负载时的逆变器输出电压和电流波形。逆变器空载起动，到达稳态后，负载电阻突然接入。此时，逆变器输出电压波形有一个小波动。经过1个周期后，恢复到正常状态。

图16为逆变器带非线性负载时的输出电压和电流波形。实验中，负载侧所接非线性负载为电阻串联电力二极管。从图16可以看出，电力二极管在输出电压波形的正半周处于导通状态，在负半周处于反向截止状态，负载电流波形为正弦半波。逆变器的输出电压波形除了在前2个周期有些畸变外，其余周期的波形基本与带线性负载时的电压波形相同。

图15 逆变器突加负载时的输出电压和电流Fig.15 Voltage and current of inverter when load is added suddenly

图16 非线性负载时带自适应估计器的输出电压和电流Fig.16 Output voltage and current with adaptive estimator in nonlinear load

5 结 论

本文针对电压型微电网逆变器，提出一种基于自适应估计器的电压波形跟踪控制策略。控制系统由电压比例控制器和自适应估计器组成。电压比例控制器进行电压波形跟踪控制，自适应估计器快速补偿各种扰动引起的动态压降，保证了系统的动态跟踪性能。本文在各种负载条件下分别进行了仿真和实验，结果表明：系统具有较好的快速响应性能和较高的稳态精度，对各种扰动具有较强的抑制能力。逆变器电压输出波形质量较高，谐波畸变率THD仅为2.6%(标准为THD≤5%)。

[1] BLAABJERG F, CHEN Zhe, KJAER S B. Power electronics as efficient interface in dispersed power generation systems[J]．IEEE Transactions on Power Electronics, 2004, 19(5): 1184-1194．

[2] BLAABJERG F, TEODORESCU R, LISERRE M, et al. Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1398-1409.

[3] 吴晓新, 柳巍, 阮毅, 等. 一种SVPWM过调制算法及其在两电平逆变器中的应用[J]. 电机与控制学报, 2016, 19(1): 76-81.

WU Xiaoxin, LIU Wei, RUAN Yi,et al.SVPWM over-modulation algorithm and its application in two-level inverter[J]. Electric Machines and Control, 2016, 19(1): 76-81.

[4] 许德志, 汪飞, 阮毅, 等. 多逆变器并网系统输出阻抗建模与谐波交互[J]. 电机与控制学报, 2014, 18(2): 1-7.

XU Dezhi, WANG Fei, RUAN Yi, et al. Output impedance modeling and harmonic interactions of multiple inverters grid-connected system[J].Electric Machines and Control, 2014, 18(3): 1-7.

[5] XUE Yaosuo, CHANG Liuchen, KUAER S B,et al. Topologies of single-phase inverters for small distributed power generators: An overview[J].IEEE Transactions on Power Electronics, 2004, 19(5): 1305-1314.

[6] 陈宏志, 刘秀翀, 钱晓龙, 等. 一种高性能单相正弦逆变电源的多环控制策略[J]. 东北大学学报, 2007, 28(12):1685-1688.

CHEN Hongzhi, LIU Xiuchong, QIAN Xiaolong, et al. A multiloop feedback control strategy for high performance single phase power supply through sinusoidal inverter[J].Journal of Northeastern University, 2007, 28(12):1685-1688.

[7] BOJOI R I, LIMONGI L R, ROIU D, et al. Enhanced power quality control strategy for single-phase inverters in distributed generation systems[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 798-806.

[8] MATTAVELLI P．An improved deadbeat control for UPS using disturbance observers[J]. IEEE Transactions on Industrial Electronics, 2005, 52(1): 206-212.

[9] 刘飞, 邹云屏, 李辉. 基于重复控制的电压源型逆变器输出电流波形控制方法[J]. 中国电机工程学报, 2005, 25(19): 58-63.

LIU Fei, ZOU Yunping, LI Hui. The repetitive control algorithm based current waveform correction for voltage source inverters[J]. Proceedings of the CSEE, 2005, 25(19): 58-63．

[10] ESCOBAR G, HERNANDEZ-BRIONES P G, MARTINEZ P R, et al. A repetitive-based controller for the compensation of 6l±1 harmonic components[J]．IEEE Transactions on Industrial Electronics, 2008, 55(8): 3150-3158.

[11] 何朕, 王广雄. 基于广义系统观测器的电池荷电状态估计[J]. 电机与控制学报, 2016, 20(1): 94-98.

HE Zhen, WANG Guangxiong.Descriptor system observer-based state-of-charge estimation for batteries[J]. Electric Machines and Control, 2016, 20(1):94-98.

[12] 刘新民, 邹旭东, 康勇, 等. 带状态观测器的逆变器增广状态反馈控制和重复控制[J]. 电工技术学报, 2007, 22(1): 91-95.

LIU Xinmin, ZOU Xudong, KANG Yong, et al. An inverter based on state-feedback integral control and repetitive control technology with state observer[J]. Transactions of China Electrotechnical Society, 2007, 22(1): 91-95.

[13] WILLMANN G, COUTINHO D F, PEREIRA L F A,et al. Multiple-loop H-infinity control design for uninterruptible power supplies[J]. IEEE Transactions on Industrial Electronics, 2007, 54(3): 1591-1602.

[14] CASTILLA M, MIRET J, MATAS J, et al. Linear current control scheme with series resonant harmonic compensator for single-phase grid-connected photovoltaic inverters[J]. IEEE Transactions on Industrial Electronics, 2008, 55(7): 2724-2733.

[15] HAO Xiang, YANG Xu, LIU Tao, et al. A sliding-mode controller with multiresonant sliding surface for single-phase grid-connected VSI with an LCL filter[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2259-2268.

[16] ZHANG Huaguang, LIU Zhenwei, HUANG Guangbin,et al. Novel weighting-delay-based stability criteria for recurrent neural networks with time-varying delay[J]. IEEE Transactions on Neural Networks, 2010, 21(1): 91-106.

[17] ZHANG Huaguang, XIE Xiangpeng, TONG Shaocheng. Homogenous polynomially parameter-dependent H∞ filter designs of discrete-time fuzzy systems[J]. IEEE Transactions on System, Man and Cybernetics, Part B， 2011, 41(5):1313-1322.

[18] WU Tsaifu, SUN Kunhan, KUO Chialing, et al. Predictive current controlled 5-kW single-phase bidirectional inverter with wide inductance variation for DC-microgrid applications[J]. IEEE Transactions on Power Electronics, 2010, 25(12): 3076-3084.

[19] BUSO S, FASOLO S, MATTAVELLI P. Uninterruptible power supply multiloop control employing digital predictive voltage and current regulators[J]. IEEE Transactions on Industry Applications, 2001, 37(6): 1846-1854.

[20] MATTHEW C T, CHEMMANGOT V N. DC Bus compensation for a sinusoidal voltage-source inverter with wave-shaping control[J]. IEEE Transactions on Industrial Electronics, 2008, 55(10): 3661-3669.

[21] HE Jinwei, LI Yunwei. Analysis, design, and implementation of virtual impedance for power electronics interfaced distributed generation[J]. Transactions on Industry Applications, 2011, 47(6): 2525-2538.

[22] HE Jinwei, LI Yunwei, GUERRERO J M, et al. An islanding microgrid power sharing approach using enhanced virtual impedance control scheme[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 5272-5282.

(编辑：刘琳琳)

Tracking control strategy for microgrid inverter with adaptive estimator

YAN Shi-jie1， YAN Wei-hang2， GAO Wen-zhong2

(1. College of Information Science and Engineering, Northeastern University, Shenyang 110819, China; 2. Department of Electrical and Computer Engineering, University of Denver, Denver 80208, USA)

Output voltage waveform of microgrid inverter is distorted when a local nonlinear load is connected. In order to solve this problem, a tracking control strategy was presented based on adaptive estimator for microgrid inverter. In this control strategy, an adaptive estimator was constructed to estimate voltage drops of microgrid inverter due to all kinds of disturbance. Then these voltage drops were used as feed-forward compensation, and voltage control vector of inverter was obtained. To achieve the real-time tracking of microgrid voltage,the concept of virtual impedance was introduced and some voltage drops are equivalent to voltage on the virtual impedance. These voltage drops may be generated by harmonics, inductor and resistor parameters variation on the filter, or a variety of external disturbance. On this basis, relative to harmonics or disturbances, the system estimates these equivalent virtual impedances to modify parameter of adaptive estimator. Therefore, the quality of waveform of the inverter output voltage is improved. The simulation and experiment which were carried out under various loads and the good control effect was achieved.

microgrid inverter; adaptive estimator; virtual impedance; nonlinear load; tracking control

2015-01-06

国家自然科学基金(61428301)

闫士杰(1964—),男,博士,副教授, 研究方向为微电网、电力变换和新能源发电；

闫伟航(1992—),男,博士研究生, 研究方向为电力系统和智能电网；

闫士杰

10.15938/j.emc.2016.11.002

TM 464

A

1007-449X(2016)11-0010-08

高文忠(1968—),男,副教授,研究方向为电力系统、电力电子和新能源发电。