蒙蒂·霍尔问题的认识及思考

☉江苏省东台市实验中学崔恒刘

蒙蒂·霍尔问题的认识及思考

☉江苏省东台市实验中学崔恒刘

概率学中，有一个经典的案例，叫“蒙蒂·霍尔问题”，又称为“车羊问题”或“三门问题”，源自美国的一个电视游戏节目，因为最后的结论与常人头脑中的固有认识不一致，引起了人们极大的兴趣，大家众说纷纭，笔者也倍感困惑.通过在初中数学骨干教师群中与网友的交流，静心思考，终于想明白了其中的道理，列夫·托尔斯泰说：“知识，只有当它靠积极的思维得来，而不是凭记忆得来的时候，才是真正的知识.”在此与同行们分享笔者的思考理解经历.

一、蒙蒂·霍尔问题

有三扇门，其中一扇门后面是一辆轿车，另两扇门后面各有一只羊.给你一次猜的机会.猜中羊可以牵走羊，猜中轿车可以开走轿车.当然大家都希望能开走轿车.现在假如你猜1号门后面是轿车，然后主持人把无轿车的一扇门（比如2号门）打开.现在再给你一次机会，请问你是否要换3号门？

二、流行观点

观点二：假定主持人打开的是2号门，既然2号门后面没有轿车，那么轿车要么在1号门后面，要么在3号门后面，概率各是，所以不必换.观点三：轿车在1号门后面的概率是，于是在2号门或3号门后面的概率就是，现在既然2号门后面没有轿车，所以轿车在3号门后面的概率为，因此应该换.

观点四：由于你并不知道哪个门后面是轿车，所以你的第一次选择是随机的，可能有以下三种出现情况：选中1羊门；选中2羊门；选中有轿车的门.这三种出现的可能性是一样的.而主持人知道每个门后面的情况，所以你的每一种选择换门的结果如下：①你选中1羊门，主持人打开2羊门给你看，你换门选中轿车；②你选中2羊门，主持人打开1羊门给你看，你换门选中轿车；③你选中轿车，主持人打开1羊门或者2羊门给你看，你换门选中剩下的2羊门或者1羊门.这样，换门选中轿车的概率为，虽然换不一定能选中轿车，但是换后选中的概率大，当然应该选择换了.

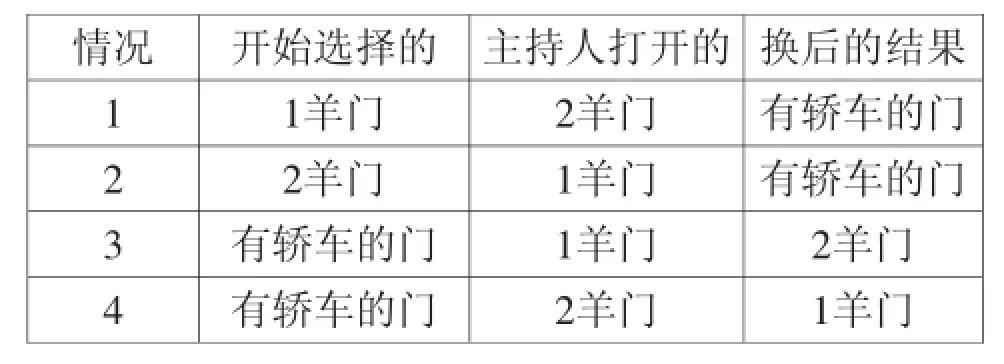
观点五：通过表格的形式给出所有等可能的结果.

情况开始选择的主持人打开的换后的结果1 1羊门2羊门有轿车的门2 2羊门1羊门有轿车的门3有轿车的门1羊门2羊门4有轿车的门2羊门1羊门

与观点四的不同之处在“当你选中有轿车的门后，主持人打开1羊门与打开2羊门给你看”看作是两种等可能的结果.从表中可以看出：共有四种等可能的情况，其中换后有轿车的两种，换后无轿车的也是两种，因此选中“有轿车的门”的概率是=，因此不必换.

专家观点：据说哈佛大学的概率学权威Diaconis教授曾接受电视台的邀请解说，他在台上当场邀请观众一起进行实验.他以一张红桃扑克牌表示轿车，两张黑桃扑克牌表示羊.按照规则要求，在台上和现场的观众进行了8次互动实验，结果是有6次显示应当换.Diaconis教授解说：每一次实验的结果事先都不知道，但是试验次数多了能够帮助我们做一些判断，概率的判断是依靠大量实验才获得的.如果这个游戏允许多次重复，那一定是“换”为好.如果只给你一次机会，那是很难说的.

这是一个概率决策问题，结论只有换与不换两个，看上去很简单，却引起人们极大的兴趣，众说纷纭，足以看出概率问题是有一定难度的.

三、分析理解

能不能获得轿车是随机的，如果开始选中的一扇门后面确实是轿车，恭喜你猜对了，此时要是换的话反而得不到轿车.如果开始选中的一扇门后面没有轿车，此时换就能得到轿车.那么“换与不换”应该以什么为依据？在这个问题中，应该以得到轿车的概率大为依据，或者根据实验进行判断，也可用计算机模拟实验来证实.

观点一到五在用概率思想方面是一致的，造成不同结果的原因在于对概率大小的判断上.在这个问题中，必须要注意的一点是，主持人是知道轿车在哪扇门后的.换的结果是将轿车换成羊，或将羊换成轿车.选择1号门，得到轿车的概率为，得到羊的概率为.如果换3号门，得到羊的概率为，得到轿车的概率为.从概率决策的角度应该换，观点三、四是正确的.观点五错在后两种情况对选择人来说应该是一种基本事件，严格地讲这个应该是条件概率，因为对原题来说，在你先行选择后，主持人打开了剩下的两扇中没有轿车的一扇门.你可这样来理解：将问题稍作改动，假设不是三扇门而是1000000扇门供你选择，在你选定一扇门之后，主持人打开余下的藏有山羊的999998扇门后问你“换不换”？这样问题是不是变得很清楚了，改变主意确实是最好的策略，毕竟，你最初选择获得轿车的概率是一百万分之一，当主持人打开余下的藏有山羊的999998扇门后，你感觉你是极幸运的，在几乎是天文数字中选中了轿车，还是来一次新的选择，换剩下的那扇未打开的门，轿车在剩下的那扇未打开的门后的可能性更大呢？其实这时也就相当于999998扇门的一百万分之一有轿车的概率都给了“剩下的那扇未打开的门”！其实将大多数不可能的情况剔除后当然会增加余下的概率.

有了上面的分析特别是这个变式问题，再来看看解释：“在主持人打开2号门之前，选择1号门，得到轿车的概率为，得到羊的概率为，也就是说，选择2号门或3号门得到轿车的概率为，当主持人打开2号门并已证实是羊之后，这就附加了条件.原来是2号门和3号门两扇门共同具有的概率，现在已经排除了2号门有轿车的可能性，这个概率就为3号门所独有.因此这时选择3号门有轿车的概率就为，比起1号门的概率，自然果断选择换.”能理解吗？

最后，再看看Diaconis教授的观点，毫无疑问，是正确的.既然人们在概率大小的判断上有分歧，那我们就通过重复模拟实验（现在还可用计算机模拟实验），借助频率的大小来判断最有说服力.用频率估计概率的原则是大量实验的频率是概率的近似值，根据实验进行判断是一个正常的思维过程，实验次数则决定判断的准确性的一种条件.Diaconis教授虽然只进行了8次实验，但这是在他对结论已经有了明确的认识的基础上实验的，Diaconis教授对这个概率问题了然于心，实验只是他让普通人认识概率的一种手段，所以8次是否是大量值得怀疑，但是不能用理论结果来证明这个结论的错误，因为所谓的估计就是已经明确了结论是不准确的，要想准确就要增加试验次数.这可以用计算机模拟实验来证实.

四、反思提升

（1）一个数学问题，如何讲解让学生感到通俗易懂，直白明了，我们教师还是大有作为的.像“蒙蒂·霍尔问题”，老师只要将问题稍作改动，将“三扇门”改为“1000000扇门”，学生理解这个概率决策就容易多了.同一个问题不同的人讲会有不同的效果，作为老师，如何讲解让学生有兴趣，感觉易懂，还是大有学问的，我们平时要多研究做这方面的有心人.

（2）概率是比较抽象，它是随机事件发生的可能性大小的度量.对于概率的研究，在教学中多结合实例，让学生亲自经历随机现象的探索过程，亲自动手进行实验，收集实验数据，分析实验结果，并将所得结果与自己的猜测进行比较.在本案例中，Diaconis教授为了让大众澄清错误的认识，接受他的结论，提供的方法就是使大众亲身参与实验，用实验的事实结果修正自己的错误认识，自然地接受他的教育.在《课程标准（2011年版）》案例40的说明中也给出了这种实验推断背后的科学依据，也就是虽然不能保证估计得完全一致，但能保证在一定试验次数下，估计值与实际情况相差不大的可能性是很大的.因此，在教学中，教师要注重创设情境，舍得花时间通过在相同条件下做大量的重复试验，让学生在实验过程中感受建构随机观念，知道可以用频率来估计概率，丰富学生对概率意义的理解，让学生在解决实际问题的过程中逐步理解频率与概率，形成概率观念.同学们虽然有一些生活经验，这些经验也是同学们学习概率的基础，但其中往往有一些是错误的，逐步消除错误的经验，建立正确的概率直觉是概率教学的一个重要目标.

（3）古典概型也叫传统概率，其定义是由法国数学家拉普拉斯（Laplace）提出的.如果一个随机试验所包含的基本事件是有限的，且每个基本事件发生的可能性均相等，则这个随机试验叫作拉普拉斯试验，这种条件下的概率模型就叫作古典概型.一个试验是否为古典概型，在于这个试验是否具有古典概型的两个特征——有限性和等可能性，只有同时具备了这两个特征的概型才是古典概型.在第三学段，课标中概率部分的要求是需要通过列表、画树状图等方法列出简单随机事件所有可能的结果，以及指定事件发生的所有可能结果.特别地，学生将从对可能性的定性描述，到刻画简单随机事件发生的概率，即定义事件｛x=k｝发生的概率为P（x=k）=，这个定义被称为概率的古典定义.这里需要注意的是Diaconis教授通过实验解决问题，给我们的启示：我们学习概率，目的不是会算几个事件发生的概率，因此，我们在教学中不能简单地将其教成会运用概率的古典定义计算事件的概率，学习课标，感受到第三学段概率课程中更重要的目标是体会概率的意义和作用，而不仅仅是计算一些事件发生的概率，因此，我们在教学中不能将这部分内容简单处理成单纯的计算内容，而要更关注在实际问题中学生对概率意义的理解.当然在第三学段的教学中，我们是经常利用树状图列举事件的所有可能性，并借此树状图算出概率.这里值得注意的是，在第三学段的很多问题中，树状图列举的每个结果，它们的可能性必须是相同的，这是利用树状图解决概率题的前提.

1.何庆青.概率小故事两则［J］.中学生数学（初中版），2013（8）.

2.史宁中.数学课程标准（2011年版）解读［M］.北京：北京师范大学出版社，2012.H