思路生成贵在自然,一题一课追求简约——一道考题的思路突破与习题课设计
2016-12-07江苏省徐州市第三十四中学孙莉
☉江苏省徐州市第三十四中学孙莉
思路生成贵在自然,一题一课追求简约——一道考题的思路突破与习题课设计
☉江苏省徐州市第三十四中学孙莉
每年中考之后,专业刊物上会有很多研究较难考题思路的文章,作者往往从解题的角度偏重于一题多解的探讨,也有多解归一、解法自然、拓展深化的研讨,然而把解题研讨转向解题教学研究的文章还不多见,本文以一道中考题为例,先给出思路突破(基于思路自然生成的角度),再围绕这道考题给出习题课的教学设计,提供研讨.
一、考题思路突破与解后反思
考题如图1所示,在梯形ABCD中,AB∥DC,∠B= 90°,AD=15,AB=16,BC=12,E是边AB上的动点,F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)求线段CD的长;
(2)如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.

图1
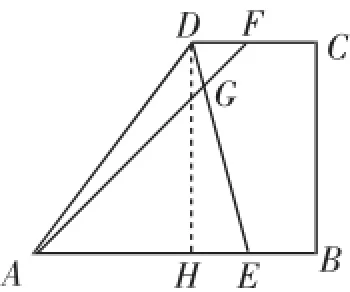
图2
1.思路突破
(1)只要过点D作出梯形的高DH(如图2),将梯形分成直角三角形和矩形,即可获得思路,求出CD=7,限于篇幅,过程略去.
(2)利用∠AGE=∠DAB,再结合∠AEG=∠DEA,可得△AEG∽DEA.由题意,△AEG是以EG为腰的等腰三角形,需要考虑两种可能:EG=AG或EG=EA;对应着另一个相似的三角形ADE中,则是两种可能:AE=AD或AE=DE.以下分两种情况求解:
第一种情况:当AE=AD时,直接可以得到AE=15(注意验证此时点E是否在边AB上即可);
第二种情况:当AE=DE时,构造图3,分析如下:作DH⊥AB于点H,由(1)中求解可知,AH=9,设AE=x,则DE=x,HE=x-9,在Rt△DEH中,根据勾股定理,可求出x=.
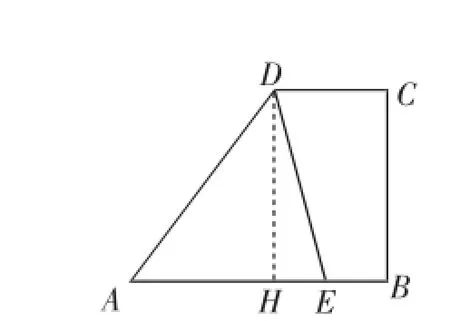
图3
(3)首先分析问题,可以有两组相似三角形供选用,并带来比例式.这就是△AEG∽△DEA,可得=,即x2=GE·DE;又△DFG∽△EAG,可得=,运用比例性质变形得
接下来,重点处理用含x或y的式子表示GE、DE,就可以沟通x、y之间的关系了.构造图2,由图2可知,HE=x-9,在Rt△DEH中中,得,再把GE、DE的表达式代入“x2=GE·DE”中,可得
现在再来分析自变量x的取值范围,首先是由(2)中得出的x=,这是一个极端位置,此时点F、D、G均重合,由题意点F不与端点D重合,故此种情况舍去,即x<;当点F运动到另一极端位置C点时,连接AC,如图4,此时,当点E恰在垂足H处时,经过演算有,满足∠AGE=∠DAE,考虑到点F不与点C重合,因而x>9,综上,x的取值范围为9<x<.
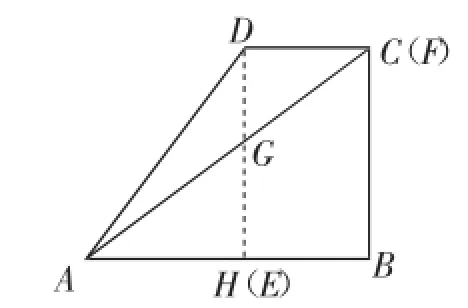
图4
2.解后反思
对于第(2)问的求解,如果不能有效转化目标,即思考△ADE,而是把思路盯在△AEG中,试图构造可能的等腰三角形AEG,则会花费更多时间,造成解题的时间成本偏高,影响其他试题的解答.
第(3)问延续了上海中考数学卷的一贯的风格,并不是初中阶段常见的三种初等函数(一次函数、二次函数或反比例函数),而需要分析具体线段之间的数量关系,通过勾股定理、相似三角形、比例式变形等综合之后,沟通x、y之间的数量关系.在演算过程中,式子不宜急于展开或化简,因为随着后续运算,会出现两个式子相乘,可以简化运算.这里也对繁杂算式化简的预见性提出了较高要求,即运算过程并不一定随时随刻都要保持算式的简洁.
另一个难点是,自变量x的取值范围.可以受到第(2)问的启示,思考可能的极端位置来获得思路,即当点F在端点C、D处时,分析此时G点的位置,相应地推理出点E的位置.启发学生想到极端位置来思考,需要教学中多加重视.
二、“一题一课”的微设计
以下以上海这道中考题为例,给出“一题一课”的微设计,提供研讨.
教学环节一:围绕梯形的热身问题
问题1:如图5,在梯形ABCD中,AB∥CD,∠B=90°,AD=15,AB=16,BC=12.
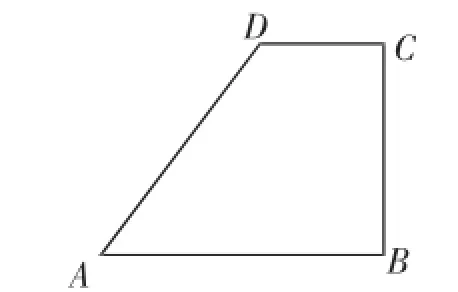
图5
(1)求∠A的正切函数值;
(2)求CD的长;
(3)求梯形ABCD的面积;
(4)设梯形的高DH与对角线AC交于M点,求DM的长.
设计意图:通过一组梯形相关的计算求值,让学生能熟练地求出直角梯形中锐角的三角函数值、梯形的面积及对角线等基础问题,为后续问题的探究奠定基础.
教学环节二:一个边上的动点探究
问题2:在“问题1”题干的基础上,若AB边上有一点E,连接DE.
(1)求线段DE的取值范围;
(2)当△ADE的面积恰为梯形ABCD面积的一半时,求AE的长;
(3)当△ADE是等腰三角形时,求AE的长;
(4)当DE取得最小值时,连接AC交DE于点G,求证:AE2=EG·ED.
设计意图:通过在边AB上增设一个动点E,设计了系列追问,为后续两个动点的研究提供基础;同时也对应着原考题中的第(2)、(3)问的设问方向.
教学环节三:引入双动点的探究
问题3:在“问题1”题干的基础上,若AB边上有一点E,射线CD上有一点F,连接DE,AF,设射线ED和射线AF交于点G(如图1).
(1)当AE2=EG·ED时,△ADE与哪些三角形相似?直接写出来.
(2)当∠AGE=∠DAE时.
①求证:△DFG∽△EDA;
②若△AEG是以EG为腰的等腰三角形,求AE的长;
③若点F在边CD上(不与点C、D重合),设AE=x,DF= y,直接写出y与x之间的函数关系式;并指出x的取值范围.
设计意图:通过层层递进式的追问,把原考题中的第(2)(3)问渐次呈现出来,提供优秀学生挑战和思考,教学时注意引导学生辨析“强化条件”的限制作用.
教学环节四:引导回顾与反思
回顾问题1:在上面“问题3”求解x的取值范围时,与之前的“问题2”“问题1”之间有没有联系?
回顾问题2:这道题目成功求解之后,你觉得对相似三角形和锐角三角函数之间的关系有怎样的认识?
回顾问题3:梯形中常用的辅助线有哪些?你能说说这些常用的辅助线的作用吗?
回顾问题4:动点问题的探究中,有人认为要特别注意一些极端位置(或特殊位置)的思考,你觉得在本题中,有哪些极端位置是值得注意的?一些具体的追问,还可结合教学对话中学生不同的思考给出.
设计意图:引导学生重视和善于解后回顾反思,以达到加深对问题求解的认识或理解.
三、开发“一题一课”的三点思考
1.铺垫问题,基础出发,渐次生长
“一题一课”的教学设计,开课阶段一定要平缓起步,坚持从基础出发,让更多的学生参与到初始问题的思考中来,能否更大范围地调动所有学生的思维是这种课型的实施关键.如果开课阶段就有不少学生不能理解初始问题,试想整节课的教学效果可能就会大打折扣,面向全体学生也就成了一句空话.特别是,如上文中的“微设计”的第一个教学环节,基础问题的设计又要服务于后续问题,即让这些基础题练习之后有助于思考后面渐次生长出来的能力题、提高题、拓展题,这就需要教师设计时充分关注后续问题的生长.
2.增设条件,靠近考题,启发思考
在基础题引导更多学生参与之后,就可陆续增设条件,靠近原来考题渐次增加强化条件,也不宜全盘托出,需要有必要的铺垫,保持基础偏弱学生探究的兴趣和信心,因为根据教学经验,当变式距离过大时,不少中等偏下的学生往往会放弃跟进思考,从而影响整体教学效果.有时在思维障碍点、解题难点处,教师可以通过必要的追问,让一些优秀学生重复讲解他们是如何突破问题的关键点、难点的,也有助于让更多的学生理解、贯通思路.
3.引出原题,自主发现,引导反思
我们认为,直到课堂教学时间进行到一半时,才适合全盘引出原题,这时要尽可能让学生在前面铺垫问题的启发下自主发现思路,保持优秀学生独立探索思路的自信和挑战的乐趣.对于特别难的拓展题,明显不适合数学基础偏弱的学生,这时可以适当取舍,比如多解问题,只要求他们先理解其中某一种简单的情形,或者问题聚焦在某个特殊图形上,请他们参与讲解对这个特殊图形中某些数据特征的理解等.特别是,在解答之后,如上面“教学环节四”一样,安排必要的回顾反思的问题,引导学生学会回顾反思,能更好地洞察和揭示难题的结构,懂得转化的路径,积累同类题的解题经验.
1.钟启泉.“教会提问”的教学[J].基础教育课程,2014(9).
2.郑毓信.善于提问[J].人民教育,2008(19).
3.郑毓信.善于优化[J].人民教育,2008(20).H
