合理分解适当铺垫各个击破——用分解法破解压轴题

☉江南大学附属实验中学庞彦福

☉江苏苏州工业园区星湾学校李景芝

☉宁夏灵武市第五中学陈红霞

合理分解适当铺垫各个击破——用分解法破解压轴题

☉江南大学附属实验中学庞彦福

☉江苏苏州工业园区星湾学校李景芝

☉宁夏灵武市第五中学陈红霞

一次听初三复习课，教学内容是如何解决综合类问题.课堂上授课教师呈现了学校中考模拟试卷中的压轴题.题目如下所示.

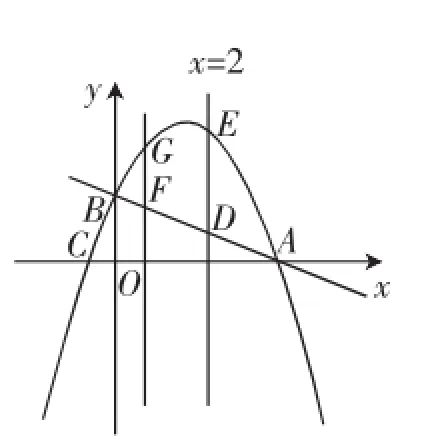
图1

（1）求b、c的值.

（2）平行于y轴的直线x=2交直线AB于点D，交抛物线于点E.

①点P从原点O出发，沿x轴的正方向以1个单位/秒的速度运动，设运动时间为t，过点P作x轴的垂线与直线AB交于点F，与抛物线交于点G，当t为何值时，FG∶DE=1∶2？

②将抛物线向上平移m（m＞0）个单位后与y轴相交于点B′，与直线x=2相交于点E′，当E′O平分∠B′E′D时，求m的值.

作为初中数学综合题目，本题具有一定代表性.但是，本节课针对该题体现出来的解题教学是不成功的.主要体现在：其一，除较为简单的第（1）问学生能够自主解决外，对第（2）问的两个问题“求t”及“求m的值”学生基本上无法自主完成；其二，当学生在第（2）问的第一个问题求满足条件的“t的值”受阻时，执教教师出现急躁情绪，往下的分析思路与解题过程基本上是老师替代了学生，已经没有了学生思维上的真正参与；其三，课后学生做当天匹配作业时，除较为简单的第（1）问外，第（2）问、第（3）问基本上没有写.

经了解学生得知，题目第（2）问的第一个问题中不会求FG，教师讲的也没有听明白，自己班又不是好班（在学生心目中，“好班”是指同一个年级中经过筛选，成绩好的学生所在班级），看到难的题目就不想写了.笔者任课的班级也是年级中基础相对薄弱的班级，针对成绩不够好的学生，该怎样进行综合类题目的教学呢？笔者在教学中采取的方法是将综合题进行分解，并根据学生的实际情况作适当的铺垫，以达到各个击破的策略.

一、在思维跨越处作铺垫

中考复习阶段，快初中毕业的学生回答问题的积极性与主动性较以前有明显的“弱化”，但是复习的对象是学生，复习的目的是促进学生的进一步理解，如果缺少了学生思维的参与，复习课的效果会大打折扣.基于此，笔者将上述问题分解后在自己的班级里尝试，学生绝大多数能参与其中，效果是显然的.

当问题呈现出来之后，教师先让学生思考怎样解答，当绝大多数学生表示没问题时，教师让一位平时表达还算清晰的学生A说出自己的解题思路.接着呈现问题2.

问题2：如图3，平行于y轴的直线x=2交直线AB于点D，交抛物线于点E.求DE的长.

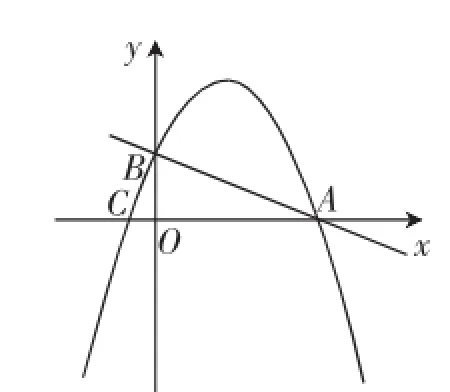
图2

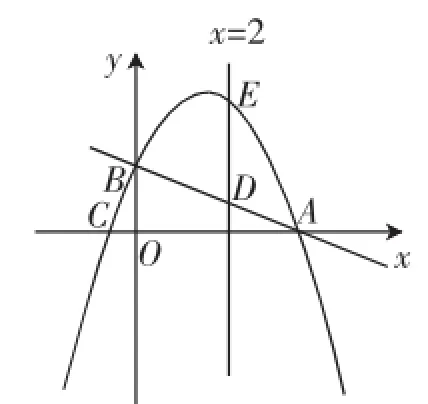
图3

教师观察到平时肯思考的学生在问题1的基础上写出抛物线的解析式y=-x2+x+2，再根据直线y=-x+2和直线x=2很快得出了点D、E的纵坐标yD=1，yE=5，于是有了DE=4.同时，教师还注意到几个后知后觉者尽管写出了抛物线和直线的解析式y=-x2+x+2和y=-x+2，但没有求出DE长的结果.教师又让一位表达较为清楚的学生B说出自己的解题思路.

学生B：就像求y轴上两点的距离一样，用上边点的纵坐标减下边点的纵坐标，因此要先根据D、E的横坐标都是2，分别代入抛物线y=-x2+x+2和直线y=-x+2中求出D、E的纵坐标，然后相减即得出DE的长.

评注：基础较为薄弱的学生解决综合类题目，除了知识储备与提取运用方面的因素，还有心理方面的障碍，譬如：怕不会、怕做错、不肯思考等.因此，教学中教师要研究学生，当学生够不到时该铺垫的要善于铺垫，当学生往上走时需要台阶的要巧设台阶.对于问题1，之所以在绝大多数学生都会的情况下仍让表达还算清晰的学生A说解题思路，目的是把应知应会的知识落实到位，使极个别会做但思路不够清晰的学生能够彻底明白.问题2对基础薄弱的学生来说是思维的一个跨越，他们往往只能解决基本的、简单的问题，也会求同一条坐标轴上两点的距离或利用勾股定理求不在同一条坐标轴上的两点的距离，但对于平行于坐标轴的直线上的两点构成的线段长往往不知道怎么下手或基本就想不到.有了学生B的提醒，这部分学生则会如醍醐灌顶、恍然大悟.这样设计，对后知后觉者来说既是思维跨越的铺垫，更为问题的进一步展开作足了准备.教学中，先知先觉者引领后知后觉者共同促进与成长是教学的一种策略.

二、在困惑处展开对话

从问题1到问题2，既有思维的跨越，也是知识运用的自然成长.有了数的坐标运算求线段长度的铺垫，再进一步拓展就有了基础和支撑，问题3的出现就不会使学生感到特别意外和茫然.

问题3：点P从原点O出发，沿x轴的正方向以1个单位/秒的速度运动，设运动时间为t，过点P作x轴的垂线与直线AB交于点F，与抛物线交于点G，如图4.

①求FG的长（用t表示）.

②当t为何值时，FG∶DE=1∶2？

问题3的①求FG的长，不少学生会将问题2的方法进行迁移，用问题2的解法来思考求FG的长.下面是教师引导学生思考的一段对话.

师：根据问题2的方法，要求FG的长需要知道什么？

众生：点F、G的纵坐标.

师：能求点F、G的纵坐标吗？

生1：从题目条件知道FG⊥x轴，P从原点O出发，速度是1个单位/秒，运动时间为t，可知点F、G的横坐标都是t，分别代入抛物线y=-x2+x+2和直线y=-x+2求出F、G的纵坐标，然后相减即可得FG的长.

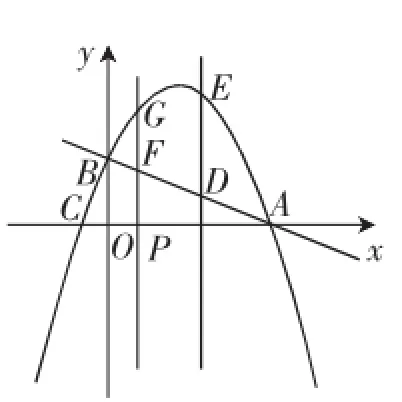
图4

师：F、G的纵坐标是具体的数吗？

生2：不是，所以题目要求用t表示.

教师看到同学们点头表示认同，就趁热打铁追问②.

生3：列个算式就能求出t的值了.

师：请同学们抓紧时间求出来吧！

不一会儿，绝大部分学生举手示意已经做好了.（教师同时观察学生的解答）

生5：还有一个答案.

师：还有一个答案（表示惊讶）？请上来结合着图说说你的想法.

师：两个一元二次方程应该得出四个值呀（追问中仍有惊讶）？

生5：t2-4t-2=0有一个解t=2-是负数，应舍去.

三、巧作铺垫静待花开

教师感觉到同学们听得很专注，表现得很认真，既想往下进行，又担心学的质量，就换着法子激将他们.老师还准备了一个往上走的问题，本想舍去，但看到同学们的出色表现，老师犹豫了，是舍掉还是继续往前走呢？教师在得到大多数学生想往前走的愿望时呈现出如下问题，并告诉同学们是选做.

问题4：将抛物线向上平移m（m＞0）个单位后与y轴相交于点B′，与直线x=2相交于点E′，当E′O平分∠B′E′D时，求m的值.

不一会儿，有好几位学生举手.

生6：问题4也不算难，画出草图，解直角三角形就可以了，m是不是-2？

师：选做的都有那么多的同学做好了.

生7（比较聪明但不够踏实）：我还以为多难呢！画出平移的抛物线后，如图5，过E′作E′H⊥y轴于H，则E′H=2，根据E′O平分∠B′E′D和E′D∥y轴，易得到OB′=B′E′，由题意知B′（0，2+m），点E′（2，5+m），所以B′E′=OB′=2+ m，B′H=5+m-（2+m）=3，在Rt△B′HE′中，即可求出m=-2.

图5

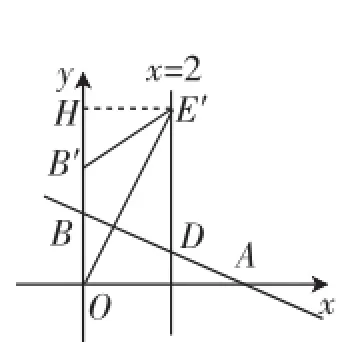
图6

师：同学们能明白吗？

大部分学生表示明白了.

师：同学们回顾一下，反思一下，这四个问题哪些是比较难的？哪些是容易出错的呢？

生8：问题3“用t表示FG的长”用的不熟.

生9：问题4中∠B′E′O=∠OE′D没有想到，如果想到了，就没啥难的了.

生10：问题3的②用字母表示FG有两种情况容易漏掉一种.

师：从几位同学的反思中，我们看到了几种共性的问题值得注意.一是字母表示数.字母运算是初一时学的，同学们不能忽略，应对的策略是首先要有用字母表示数的意识，其次运算时要细心.二是几种情况容易忽略.平时说的分类讨论要不重不漏.三是有的同学说某问题“没想到”或“想不到”，原因在哪儿？学数学就要学思维，学会思考的方法，要牢固掌握所学的知识，学会灵活运用知识解决问题的基本方法.

评注：建构主义的学习理论认为：学生的学习是从自己已有的知识和经验出发的一种自主建构的过程.教学中无论是新课还是复习，必须要研究学生，当学生思维受阻或解决问题遇到障碍时，作为数学学习的组织者、引导者与合作者的教师要多想一想原因在哪儿，教学要遵循学生学习数学的心理规律，从学生已有的知识和实际情况出发，该铺垫的要铺垫，该将问题分解的要合理分解.比如问题4的图形也可简化或分解为图6，进而使学生获得对数学本质理解的同时，在思维能力、情感态度与价值观等方面得到进步与发展.无论是复习课还是新授课，都不能靠让学生大量做题来替代理解数学，不能理解的死练往往会导致思维定势.

以学定教，因材施教.精心设计适合学生学习的教学，针对基础不够好的学生要有爱心，有耐心，用真心，做小事.譬如“低起点，小坡度”不失为一种有效的举措.“低起点”可以是知识起点低，方法起点低，易于让学生理解和操作，这样学生容易获得成功感，提高学习的兴趣.“小坡度”就是设计问题短小，提问坡度小，题型变化幅度小，可以通过变式训练，步步设问，层层递进，让学生先“想到”再进而“做到”，以达到拾级而上.“低起点，小坡度”的过程中，要注意课堂反馈要快，错题纠错要快，测试评价要快，以满足学生学习的心理需求；在要求上依然要高，做到规范要求高，思维效率高，不抑制学生的思维，让学生学会思考，学会学习.

本节课之所以这样分解与设计，主要是考虑到学生的实际情况，找准学生已有知识的起点，使问题由易到难，呈现出明显的梯度，让学生容易上手，这样新方法的生长就有了基础，学生的探究与思考就显得合情合理，水到渠成.再解决组合后的综合题时才不会产生心理畏惧.解题教学的核心是教学生学解题，关键是思路的寻找.中考中的综合类题目，对于大部分学生来说尽管不一定做完整，但还是能够尝试做一做的，不能因为学生暂时还比较薄弱，就忽略对他们的培养.教师要甘为人梯，当他们前行困难时作以铺垫，当他们想往新的目标时要搭建平台.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.卜以楼.生长型构架下实数复习课的教学实践与思考［J］.中学数学（下），2016（3）.

3.庞彦福．我曾这样对待留守儿童［J］．人民教育，2016（16）．Z