一道一模压轴题的命制过程及感悟*

☉江苏南京师范大学附属中学新城初中何君青

一道一模压轴题的命制过程及感悟*

☉江苏南京师范大学附属中学新城初中何君青

一模是全区组织的综合性检测，是中考前的一次大型诊断测试.命题须以中考及新课标的要求作为标准，其功能是让学生感受中考，同时这类考试还对后续中考第二轮复习起到指导性作用，所以无论教师还是学生都极其重视这类考试.近期，笔者命制了我区中考一模试题，压轴题以几何探究题为背景进行了考查，题目得到了全区老师的称赞.命题过程中略有收获，故撰文与同行分享.

一、原题呈现

问题提出

平面上，若点P与A、B、C三点中的任意两点均构成等腰三角形，则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形，也称点P是△ABC的巧妙点.

初步思考

（1）如图1，在等边△ABC的内部和外部各作一个△ABC的巧妙点.（尺规作图，不写作法，保留作图痕迹）

（2）如图2，在△ABC中，AB=AC，∠BAC=36°，点D、E是△ABC的两个巧妙点，其中AD=AB，AE=AC，BD=BC= CE，连接DE，分别交AB、AC于点M、N.求证：DA2=DB·DE.

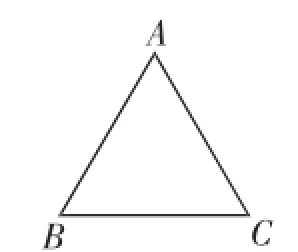
图1

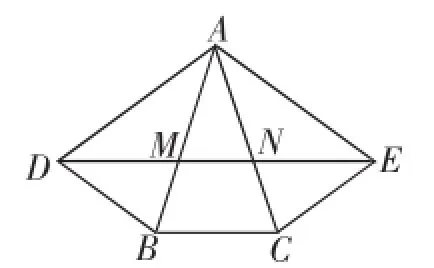
图2

深入研究

（3）在△ABC中，AB=AC，若存在一点P，使PB=BA，PA=PC，点P可能为△ABC的巧妙点吗？若可能，请画出示意图，并直接写出∠BAC的度数；若不可能，请说明理由.

分析：本题考查了尺规作图、平行线的性质及判定、黄金三角形的相关概念、等腰三角形的相关概念、全等三角形的性质与判定、相似三角形的性质与判定.本题注重思想方法的考查，蕴含了数形结合、分类讨论的思想，题目特别重视对学生能力的培养，引导教师在教学的过程中重视对数学知识间内在联系的讲解，以及基础知识、基本技能的训练，基本活动经验的培养，基本思想方法的渗透.题目在设置上螺旋式上升，第一问为作图题，旨在让学生经历发现问题、提出问题的过程，难度小，容易入手；第二问为证明题，旨在让学生经历分析问题、解决问题的过程，此问有一定的难度，学生理解巧妙点的实质后找准需要证明的一对相似三角形才能解决；第三问为探究题，旨在培养学生的空间观念和应用意识，难度较大，综合性强，区分度明显，考查学生综合运用数学知识解决问题的能力.

二、命制过程

1.初步设想

命题前，笔者查阅了近几年南京市中考试题，发现近几年中考试题压轴题主要以几何探究题为主，如2013年的顺相似、逆相似，2014年的“边边角”证明三角形的全等，2015年画等腰三角形等，试题不仅考查相似的有关性质和判定、等腰三角形的相关作图，也考查学生分析与解决问题的能力及综合运用知识的能力，试题的呈现体现出多元化的形式，开放性较大，探究味道浓.考虑到南京近几年中考试题考查的方式，笔者决定此次一模试卷的压轴题依然以几何探究题为考查载体.

之后，笔者查阅了新课标，将相似三角形、等腰三角形的考查要求仔细地研读：了解等腰三角形的概念，探索并证明等腰三角形的性质定理；了解相似三角形的判定定理；了解相似三角形的性质定理.

基于新课标的要求，鉴于此题为压轴题的定位，笔者决定命制一道难度系数为0.3，考查知识覆盖面广的试题，题目预设三问，逐步递进，题型丰富，涵盖作图、证明、解答，让各类学生都能得分，但又凸显优秀的学生.

有了明确的方向后，笔者翻阅书本相关章节，试图找到突破点，但无任何收获，庆幸的是笔者曾多次命制一模试卷，收集了不少的素材.在之前一次八年级期末考试中有这样一道题引起了笔者的注意：四边形ABCD是正方形，在正方形ABCD所在平面内找一点P，使△PAB、△PAD、△PCD、△PBC都是等腰三角形，这样的点P有______个.这道题难度不大，但却有很深的挖掘空间，于是笔者决定以此题为背景，改编试题，赋予题目“新的生命”.

2.框架形成

试题的改编、创作离不开“题源”，确定好题源后笔者准备给这个“特殊”的点起一个新的名字，让其“焕然一新”，这也正符合当下中考的模式：新定义阅读题.于是第一稿如下所示.

平面上，若点P与A、B、C三点中的任意两点均构成等腰三角形，我们则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形，也可称点P是△ABC的巧妙点.类似地，平面上，若点P与A、B、C、D四点中的任意两点均构成等腰三角形，我们则称点P是A、B、C、D四点的巧妙点，若A、B、C、D四点构成四边形，也可称点P是四边形ABCD的巧妙点.

（1）如图1，作出等边△ABC的所有巧妙点.（尺规作图，不写作法，保留作图痕迹）

（2）正方形的巧妙点的个数为________.

（3）矩形是否存在巧妙点？若存在，画出示意图加以说明，并直接写出此时矩形长与宽的比值的平方是多少；若不存在，请说明理由.

对于命题初稿，值得肯定的是本题取材合理：立足基础知识、基本技能，源于课本核心考点等腰三角形；角度新颖：着眼于学生画图时产生的问题，层层递进；题型丰富：既有填空，又有作图、解答.

3.修订完善

学生对新定义阅读题一直有较强的畏惧感，经常看到题目感觉无从下手，本着尊重学生的原则，笔者将题目的题干、图形尽可能反复修改，尽可能简洁，以减轻学生的恐惧感.一开始，笔者打算此题先考查三角形再考查四边形，增加题目复杂性，但在反复推敲修订时，笔者发现第（2）问正方形的巧妙点的个数为0，担心学生不太敢写这个答案，第（3）问计算时需要用到一元四次方程，虽然双二次方程可用换元法替换为一元二次方程，但怕被扣上超纲的帽子，于是笔者决定适当降低难度，仅考查三角形领域.故修如下.

问题提出

平面上，若点P与A、B、C三点中的任意两点均构成等腰三角形，我们则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形，也可称点P是△ABC的巧妙点.

初步思考

（1）如图1，在等边△ABC的内部和外部各作一个△ABC的巧妙点.（不写作法，保留作图痕迹）

（2）如图2，在△ABC中，AB=AC，∠BAC=36°，BC=2，点D、E是△ABC的两个巧妙点，其中AD=AB，AC=AE，BD=BC=CE，连接DE，交AB、AC于点M、N.求DE的长.

深入研究

（3）在△ABC中，AB=AC，若存在一点P，使PB=BA，PA=PC，问：点P是否可能为△ABC的巧妙点？若可能，请画出示意图、并直接写出∠BAC的度数；若不可能，请说明理由.

4.最终定稿

为了使题目更适合南京市的中考特色，给我区教师更好的后续复习指导，笔者再次仔细看了2015年南京市中考试题，发现2015年南京市中考题将相似问题作为证明题直接考查，这与历年南京的相似考题略有区别.于是笔者预测这是南京市2016年中考命题的导向，于是将题目第（2）问利用相似求线段长改为直接证明.

如图2，在△ABC中，AB=AC，∠BAC=36°，点D、E是△ABC的两个巧妙点，其中AD=AB，AE=AC，BD=BC= CE，连接DE，分别交AB、AC于点M、N.求证：DA2=DB·DE.

5.总结反思

回顾这道题的命题过程，一波三折，从一开始选定题源，到几次修改，都是以南京市历年中考试题和新课标作为参考依据.此题角度独特，探究味儿浓，很具典型性，但笔者认为此题还能加以发展，若将该题再发展到直角三角形、等腰直角三角形领域，解决更多的问题就更完美了，介于题目考查容量有限，未曾设问，确实可惜.

三、命题感悟

一模考试的目的不是为难老师、学生，而是达到共赢局面.通过考试，教师可以发现自己教学工作中的不足，从而加以重视、改善、提升，学生可以发现自己对哪些知识掌握得不牢靠，从而加以提高、完善.故每次考试前，命题老师要分析近几年当地中考的趋势，把握好考试的方向，考试后，教师、学生要好好分析从考试中发现的不足，从而尽快改进.

由于一模考试命题时间短，很多命题教师会将旧题直接拿来或者简单改编，这样会把广大备考师生引向题海，导向走偏.所以建议出卷教师在压轴题方面尽可能原创，真正诊断出考生的问题，查漏补缺，为备考师生指明正确方向.在命制压轴题时，要特别重视数学最核心的“四基”的考查：基础知识、基本技能、基本活动经验和基本数学思想方法.本题的第一问可以看作是对基础知识、基本技能的考查，第二问可以看作是对基本活动经验的考查，第三问可以看作是对基本数学思想方法的考查.

值得关注的是：数学思想的考查是数学的本质、精华所在，尤其是压轴题的考查更应建立在数学思想考查的基础上，命制的试题需精彩纷呈，逐步提升难度，螺旋式上升.引导教师在平时的教学中，要尽可能地教给学生一些提炼数学思想和本质的方法，让学生自己归纳，在比较、分析、归纳、类比、抽象中提升学生的能力.Z

南京市教育科学“十二五”规划立项课题“‘跑班’分层模式下初中数学课堂教学与考试评价研究”（课题编号：L/ 2015/181）.