从取材到命制从解题到再思考

☉福建福州第十一中学胡鹏程

从取材到命制从解题到再思考

☉福建福州第十一中学胡鹏程

笔者参加了2016年福州市中考命题工作，其中第26题是一道动态几何试题.本题的素材来源于教材，从取材到命制，从解题到再思考，经历了一个不断思考、学习的过程.现将一些思考及感悟与同行交流、分享.

一、试题取材

源自人教版《义务教育教科书·数学》八年级下册的一个数学活动：如果我们身旁没有量角器或三角尺，又需要作60°、30°、15°等大小的角，可以采用下面的方法（如图1）.

（1）对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；

（2）再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时，得到了线段BN.

观察所得到的∠ABM、∠MBN和∠NBC，这三个角有什么关系？你能证明吗？

简析：如图2，连接AN.由对称性可知∠ABM=∠MBN，且BN=BA.又因为NA=NB，可得△NAB是等边三角形，所以∠ABM=∠MBN=∠NBC= 30°.

本活动给出了一个利用矩形纸片折出30°角的方法.

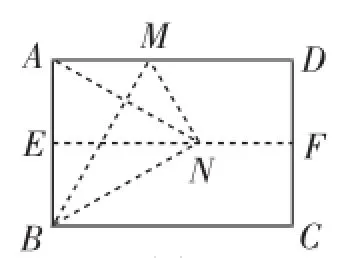
图2

二、思考探究

根据上述数学活动我们有如下思考.

思考1：本活动中两次折叠分别得到两个阶段性的结论，第1次折叠得到“EF垂直平分线段AB”，第2次折叠得到“BN=BA”，再由这两个阶段性的结论推出“△NAB是等边三角形”.

首先，所有这一系列结论都与矩形的边长无关，属于“变中的不变”；其次，由于“EF垂直平分线段AB”和“BN=BA”是相互独立的，那么这两个阶段性的结论可以独立推广.

思考2：对于“BN=BA”这个结论，从运动元素的主从关系看，点N是被动点，被点M牵制，点M运动，点N随之运动；从轨迹的角度看，点N的轨迹其实是一段圆弧.也就是说，点M在AD边上运动，点N则在以B为圆心，BA长为半径的圆弧上运动（如图3）.

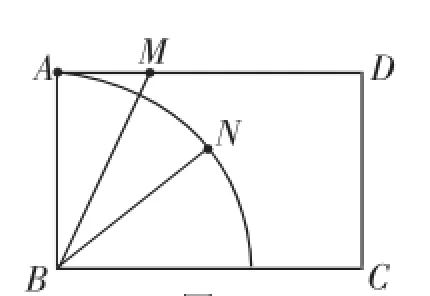
图3

三、试题命制

1.初稿

作为福州中考的“保留曲目”，动态几何试题一般都安排在压轴部分.在平面几何的背景下，让图形中的元素动起来，并用运动的观点观察问题，就可以从“一般性”和“特殊性”的角度命制动态几何试题.用函数来描述运动过程中两个目标变量之间的关系，或探索运动过程中图形所固有的性质，都属于对“一般性”的考查；而运动过程中，在限定条件下进行的计算，或研究满足某些条件的对象是否存在，则可以说是对“特殊性”考查的主要形式.

上述数学活动中，图形是学生所熟悉的，对折操作也是常见的，以此为素材命制试题，可以确保试题具有较高的信度.经过讨论，命题组将活动中的第二次操作确定为命题的核心点.

我们知道，平面内确定一个点需要两个独立条件.

从“特殊性”的角度看，一方面，由前面的分析可知，“对折”是点N的一个限制条件，对折使得点N在圆弧上运动，只要再设置一个条件，点N即可确定；另一方面，N、M两点是相互牵制的，具有对应关系，只要固定其中一个点，另外一个点也随之确定，限制点N即可对点M进行相关计算，固定点M亦可对点N展开相关计算，这样就可生成“特殊性”考查.

从“一般性”的角度思考，如果不增加条件，虽然点N及其运动所产生的量都无法确定，但可以根据其运动的范围设计出取值范围或最值问题，也就形成“一般性”的考查.如前所述，点M沿着线段AD从A向D运动时，点N在圆弧上运动，射线CN与直线AD的交点F也开始向点D运动，当CN与圆弧相切时，点F与点D的距离最近，且恰与点M重合.但是，随着点M继续向右运动，点F则开始“往回走”，并且会落到线段DA的延长线上.考虑到运动过程中，相切这个位置较为特殊，有考查价值，于是将其选为第（3）问的考点；又考虑到点F落在DA的延长线上时，没法确定最值，我们形成初稿.

如图4，在平面直角坐标系中，矩形OABC的顶点A（4，0）、C（0，3），D是边CB上一点，将△OCD沿直线OD折叠，得到△OED.

（1）当OE平分∠AOD时，求CD的长；

（2）当CD=1时，求点E的坐标；

（3）连接AE并延长，交直线BC于点F，设点F的横坐标为x，求x的最大值.

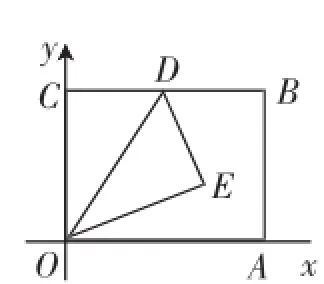
图4

2.定稿

第（1）、（2）两问其实就是一个由E定D和由D定E的互逆的过程，都属于“特殊性”的考查，第（3）问探究运动过程中的最值，属于“一般性”的考查.整道题，基本符合我们的命题意图，且问题之间还算连续，大致可以成题.但同时也存在一个致命的问题：坐标系给的很不自然.这明明就是一个平面几何背景下的动态几何试题，却安了一个坐标系进去，人为的痕迹过于明显，坐标系貌似只是为了第（3）问设问方便而建立的，其实际意义并不大.

实际上，只需要修改题目的表述，对点F的运动范围进行限制，让其落在线段BC上就可以把坐标系“拿掉”.至于第（2）问，只要点E的位置是确定的，可以计算的量就有很多，完全不受坐标系的影响.

经过讨论，命题组决定去掉坐标系，得到如下定稿.

如图5，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM.

（1）当AN平分∠MAB时，求DM的长；

（2）连接BN，当DM=1时，求△ABN的面积；

（3）当射线BN交线段CD于点F时，求DF的最大值.

三个小题有不同思维的层次，所设问题既独立又相互关联；三个问题或立足初中阶段的基本知识，或蕴含初中阶段重要的数学思想方法；去掉坐标系后，第（2）问的难度虽然稍微有所加大，但题目呈现方式自然，而且基本保留了初稿的意图；第（3）问最值问题的考查有一定的思维量，但计算量不大，体现了多思少算的精神.

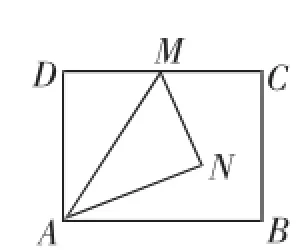
图5

3.进一步思考

对于第（2）问，我们给出以下两种解法.

解法1：如图6，延长MN交AB的延长线于点Q.

易得△ANM≌△ADM，则∠DMA=∠AMN.又∠DMA=∠MAQ，则∠AMN=∠MAQ，则MQ=AQ.

设NQ=x，则AQ=MQ=1+x.

在Rt△ANQ中，由AQ2=AN2+NQ2，可列方程（x+1）2= 32+x2.解得x=4.则NQ=4，AQ=5.

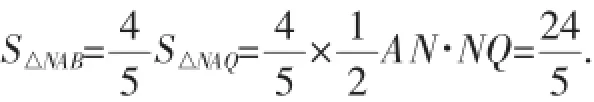
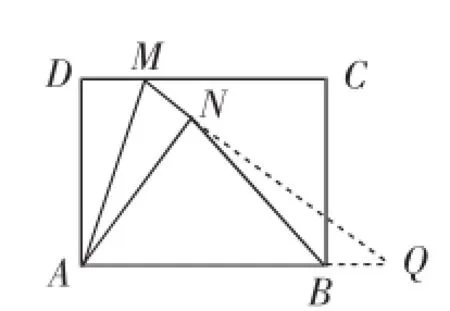
图6

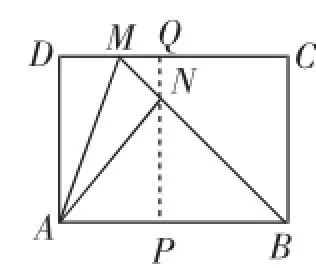
图7

解法2：如图7，过点N作PQ∥BC，分别交AB、CD于点P、Q.

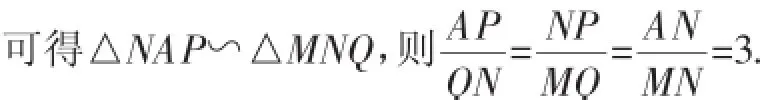
设MQ=m，则NP=3m，则AP=1+m，QN=3-3m，可列方

虽然题目本身没有问题，但在确定第（3）问的解答时又遇到一个问题：为什么BN与弧相切时DF最大？应该怎么说明？

从几何直观的角度的确能判断出BN与弧相切时，DF有最大值，通过几何画板也可以得到验证.但直观归直观，它只是解题时一个方向性的判断，不能作为最终的依据.作为解答，我们需要严谨的推理、演算.在命制动态几何试题时，很多命题者喜欢用“最值”或“取值范围”问题来压轴.不可否认，“最值”或“取值范围”问题即使是在高中也具有较强的选拔功能，但在初中阶段往往存在一个尴尬的情况：这两类问题的很多解答都采用直观代替演绎推理的做法.笔者认为这种做法不值得提倡.虽然直观很重要，但其始终不能代替逻辑推理.这是因为：数学是用抽象的眼光从客观世界的物体中提取几何图形进行研究，因此我们所研究的几何图形比它们的现实原型更一般、更纯粹，这就需要具有一般性和抽象性的方法，如果没有逻辑推理，只依靠直观，对图形的认识将难以深入，也不利于学生的长期发展.

命题组尝试着给出下列两种解法.

解法1：如图8，过点A作AH⊥BF于点H.则AH≤AN，则sin∠ABF=≤.则当点N、H重合（即AH=AN）时，∠ABF的度数最大，DF最大，此时点M、F重合，B、N、 M三点共线（如图9）.则BH=.

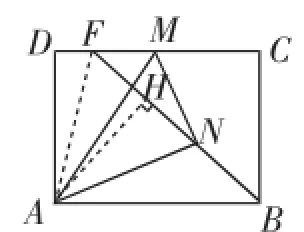
图8

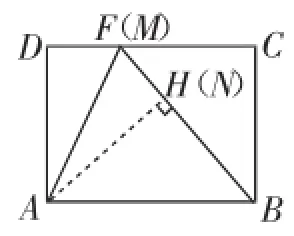
图9

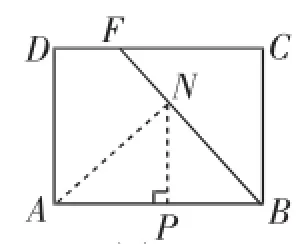
图10

解法2：如图10，过点N作NP⊥AB于点P.

由关于x的方程（k+1）x2-8kx+（16k-9）=0有实数根，得判别式△=（-8k）2-4（k+1）（16k-9）≥0，解得k≤.大且最大值为4-.

其他的一些解法，不是有“超纲”的嫌疑就是仍属于“几何直观”.上述这两种解法勉强说得过去，但毕竟不是通法，始终拿不出一个理想的解决方案.

重新分析，发现本题的运动过程中还存在着一个不变量——△ABF的面积.在M的运动过程中，△ABF的面积始终等于矩形ABCD面积的一半.三角形的面积保持不变不就是反比例的模型吗？如图11，过点A作AH⊥BF于点H，连接AF.由于面积不变，所以AH与BF的乘积也就保持不变，即BF与AH成反比例函数关系，当AH最大时，BF取最小值.又因为AH≤AN，所以当点H与点N重合时，AH最大，此时BF最小，进而可得CF最小，推出DF最大.

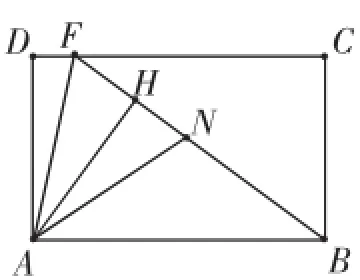
图11

本题中，在点M的运动过程中产生了BN、BF、AH、CF、DF等多个变量.我们知道，在解决多个变量的问题时，可以分析这些变量之间的关系，从中选取一个取值能影响其他变量的值的变量作为自变量，然后根据问题的条件寻求可以反映实际问题的函数，以此作为解决问题的数学模型.借助函数这个研究变量的工具，本题的解题思路显得更加清晰.这样一来，第（3）问就体现了用函数的观点分析运动过程中的变量，学生需要经过分析，选择AH为自变量，建立BF与AH之间的函数，通过反比例函数，分析点M运动过程中，BF随AH变化而变化的牵制关系，从而使问题得以解决.这更加符合我们预设的“一般性”的考查目标，于是得到下列解法.

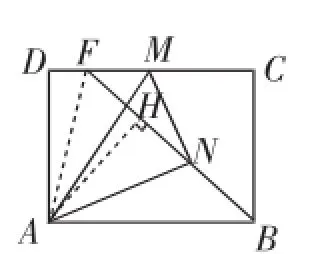
图12

由AH≤AN=3，得当点N、H重合（即AH=AN）时，DF最大.（AH最大，BF最小，CF最小，DF最大）此时点M、F重合，B、N、M三点共线.由△ABH≌△BFC，可得CF=BH=，则DF的最大值为4-.

四、写在最后

对于命制单一的一道题而言，有几个关键点值得注意：选取素材，设计问题，制定解答.在素材选取方面，各地有各自的做法，但一些经典题目或教材中的题目往往受到命题者青睐；选中素材后，对素材进行研究、改造、变式，设计出适宜的问题；选取素材和设计问题这两个环节固然重要，但制定解答这个环节也不可忽视，因为解答是对所设计问题的一个检查，它既要考虑到所用方法是否“超纲”，还应兼顾到解法的多样性及普适性.另外，试题的解答在一定程度上也会对教学起到导向作用.

1.胡鹏程.2013年福州卷第21题的命制与感悟［J］.中学数学教学参考（中），2014（8）.Z