几何综合题研究：从思路贯通到教学微设计

☉江苏省徐州市第十三中学孟慧

几何综合题研究：从思路贯通到教学微设计

☉江苏省徐州市第十三中学孟慧

几何综合题作为中考试卷的最后一题来“压轴”，这在全国各地中考试卷中并不多见.笔者关注到有些省市近年来中考试卷常常设计一道颇有区分度的纯几何综合题作为最后一道，考题涵盖了丰富的初中几何内容，有效考查了几何图形分离、识别、构造、聚焦、转化能力，达到了较好的区分选拔功能.本文选取某地中考最后一题，给出思路突破和解后反思，并构思教学“微设计”，提供研讨.

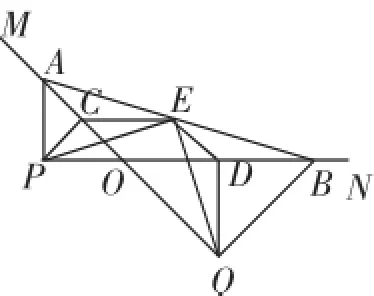
图1

一、考题及思路突破

考题（2016年某省中考卷第23题）如图1，A、B分别在射线OM、ON上，且∠MON为钝角，现以线段OA、OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP、△OBQ，C、D、E分别是OA、OB、AB的中点.

（1）求证：△PCE≌△EDQ.

（2）延长PC，QD交于点R.

①如图2，若∠MON=150°，求证：△ABR为等边三角形；

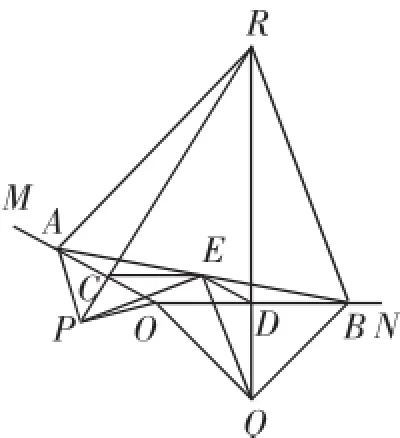
图2

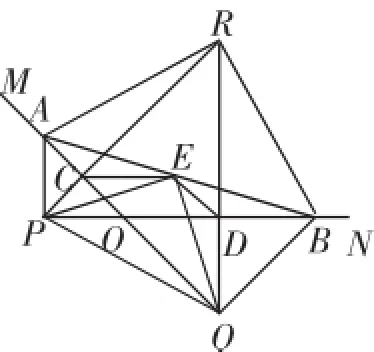
图3

1.思路突破

（1）根据很多中点的信息，可以解读出CE是△AOB的中位线，DE也是△AOB的中位线，即CE∥OB，CE=OB，DE∥AO，DE=AO.再结合△AOP、△CBQ是等腰直角三角形，可得CE=OD=QD，DE=OC=PC.

现在距离△PCE与△EDQ全等，还缺少一个条件！

继续利用上面的中位线性质可以发现一个平行四边形OCED，它的对角∠ECO=∠EDO，再结合∠PCO=∠QDO=90°，可得∠PCE=∠QDE.于是可以根据“SAS”（CE=QD，∠PCE=∠QDE，DE=PC）证出△PCE≌△EDQ.

（2）如图4，延长PC，QD交于点R后，可以运用PR垂直平分AO，QR垂直平分BO，连接OR，可得AR=BR，即△ABR是等腰三角形.

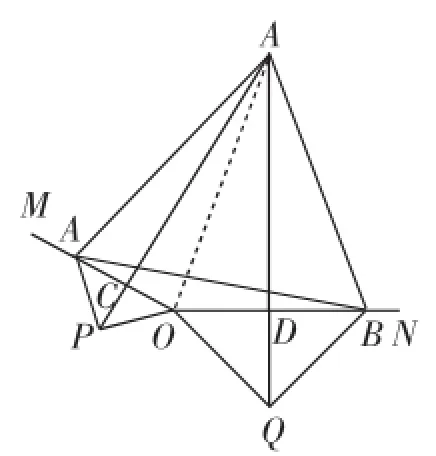
图4

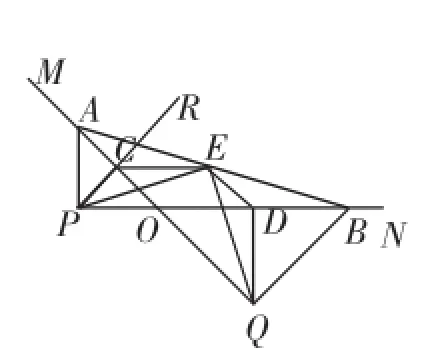
图5

①根据轴对称性质，∠ARO=2∠CRO，∠BRO= 2∠ORD，即∠ARB=2∠CRD.再把目光聚焦在四边形OCRD中，∠OCR=∠ODR=90°，∠CRD+∠COD=180°，所以∠CRD=30°.于是∠ARB=60°，再结合上面已证得的AR=BR，故△ABR是等边三角形.

②由△ARB∽△PEQ（上面的求证过程已知它们都是等腰三角形），可以确认顶角∠ARB=∠PEQ.主要难点是这两个顶角有无特殊？是否为一个特殊角度？让我们把图形中的线段简化，把目光锁定在相对简洁一些图形中，如图5，由平行四边形OCED的性质，可得∠ACE=∠CED.再结合△PCE≌△EDQ，有∠CPE=∠DEQ，∠CEP=∠DQE，而根据△CPE的外角性质，有∠RCE=∠CPE+∠CEP，这样经过代换可得∠ACR+∠RCE=∠ACR+∠CPE+∠CEP=∠CED=∠CEP+∠PEQ+∠DEQ，即∠PEQ=∠ACR=90°.这是一个非常重要的进展，随之可确定∠ARB=90°，∠CRD=30°，∠MON=135°，相应地可发现点P，O，B在同一直线上.

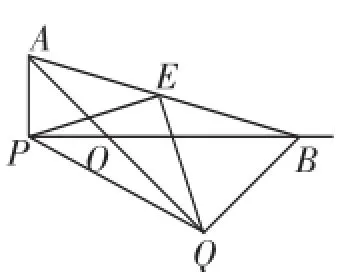
图6

2.解后反思

这是一道纯几何综合题，涉及全等、相似、平行四边形、三角形中位线等几何知识，由于图形线条繁多，造成分离、聚焦图形有一定的障碍，以下从主要障碍点的角度分析几处重要的障碍点.

障碍点之一：图形线段繁杂、条件堆砌，造成阅读理解不畅.

从第（1）问开始，图1就是线段繁多，让很多几何适应性偏弱的学生难以读下去，理解上也有困难.两个待证三角形的两组边仔细分析还可以沟通相等，但边的夹角相等却有一定的困难.

障碍点之二：发现△ABR是等腰三角形.

在图2中，生成的△ABR是一个特殊三角形（等腰三角形），需要结合PC、QD与OA、OB的特殊位置关系（垂直平分），来推出AP=BR.这对于后续问题的推理有重要的奠基作用.

障碍点之三：发现∠AEQ是直角.

最后一问只给了一个相似的条件，而需要探究∠MON的度数.将图形往特殊位置或特殊角度猜想是必要的.沿此方向，想到∠AEQ是一个特殊角度（直角），并使之成为破解最后一问的关键点.

二、解题教学“微设计”

教学环节一：特殊图形，热身练习

例1如图7，∠MON=135°，在边OM、ON上分别取点A、B，分别以OA、OB为斜边作等腰直角三角形OAP和等腰直角三角形OBQ.

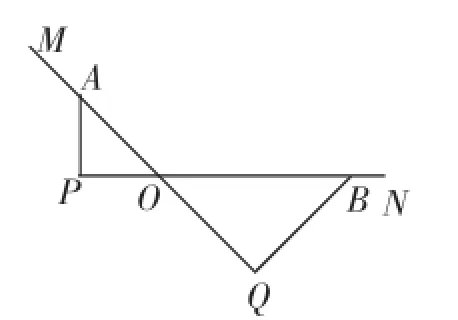
图7

（1）点P、O、B在同一直线上吗？

（2）连接AB，点A、P、Q、B是否在同一个圆上？如果在，请指出圆心的位置；如果不在，说明理由.

（3）分别取OA、OB的中点C、D，设射线PC、QD交于点R，求∠PRQ的度数.

（4）连接AB，取AB的中点为E，猜想△PEQ的形状，并说明理由.

设计意图：在特殊角度（∠MON=135°）的背景下，研究一些可能的问题，为学生理解“考题”第（2）问做些铺垫和准备.

教学环节二：旋转变换，继续探究

例2如图8，∠MON是一个钝角，点A、B在边OM，ON上，分别以OA、OB为斜边作两个等腰Rt△OAP、Rt△OBQ.取OA、OB中点C、D，设射线PC、QD交于点R，连接AP，AB，BR.

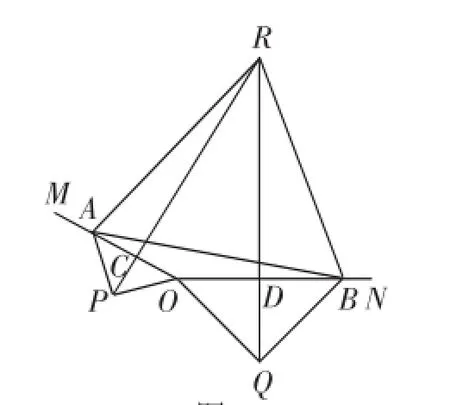
图8

（1）求证：AR=BR.

（2）小南同学经过演算，发现∠CRD与∠MON互为补角.请判断“小南的发现”是否正确？

（3）小舟同学发现：在图8中，取AB的中点E，还可证出△PEQ是等腰直角三角形.请判断“小舟的发现”的真假，并说明理由.

（4）在“小舟发现”的基础上，若△ARB∽△PEQ，求证AB=PQ.

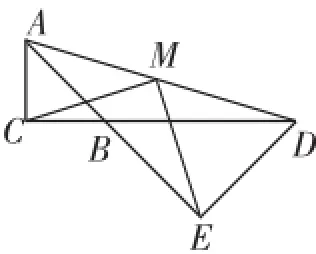
图9

教学环节三：听课检测，变式再练

听课检测题：如图9，△ABC与△BDE均为等腰直角三角形，∠ACB=∠BED=90°，连接AD，取AD中点M，连接CM，ME.

（1）当C、B、D三点在同一直线上时，求证：CM=ME.

（2）分别作△ABC与△BDE的高CF、EG，连接FM，GM，求证：△CFM≌△MGE.

（3）在（2）的条件下，若射线CF、EG交于点N，连接AN，DN，求证：AN=DN.

（4）设△ABC与△BDE的高CF、EG所在直线交于N点，连接AN，DN.

①当△AND为等边三角形时，求∠ABD的度数；

②当△AND∽△CME时，求AD CE的值.

三、写在最后

纯几何综合题作为全卷最后一题，又不得“超标”出现初中阶段没有学过的一些平几中较难的定理，那就需要在解题层次上不断增加，也就出现了像上文考题这样的繁杂图形，也使得问题的起点偏高，少部分数学适应性弱的考生可能就直接选择放弃.这让笔者想起初中有理数运算中的如下两种算式：

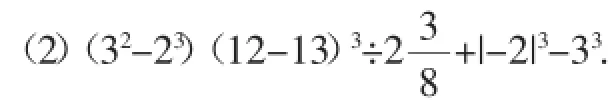
根据教学经验，即使有理数运算这一章学完之后，能成功把这两道算式准确、快速算出来的学生也不会超过一半，而逐个展开，有序地让他们订正后，又往往会成功算出.这说明学生在面对综合多次、解题层次增多后，常常容易顾此失彼，受阻某一环节或某一步骤之后，也就最终不能贯通问题.这是不是也提醒我们，在限时检测的“高利害”考试命题中，对于增加解题层次这一命题技术的控制也要谨慎呢？一方面是数学求简的本质追求，另一方面也是把教学导向“多想少算”的追求吧！

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

3.夏盛亮.引导回归教材，倡导开放取向——一次县级期末卷的命题取向分析［J］.中学数学（下），2014（1）.

4.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.H