理性思考严谨推理优先概念*——以“2016年厦门市中考第9题”为例

☉福建厦门第一中学王淼生

理性思考严谨推理优先概念*——以“2016年厦门市中考第9题”为例

☉福建厦门第一中学王淼生

一、真题呈现

刚刚落下帷幕的2016年厦门市中考试题第9题（以下简称题1），原题如下所示.

题1：某种动物活到20岁的概率为0.8，活到25岁的概率为0.6，则现年20岁的这种动物活到25岁的概率为（）.

A.0.8 B.0.75 C.0.6 D.0.48

其实，文1第148页“拓广探索”栏目也有一道类似试题（以下简称题2），原题如下所示.

题2：动物学家通过大量的调查估计：某种动物活到20岁的概率为0.8，活到25岁的概率为0.5，活到30岁的概率为0.3.

（1）现在20岁的这种动物活到25岁的概率为多少？

（2）现在25岁的这种动物活到30岁的概率为多少？

二、参考答案

对于上述题2，文2第268页给出以下参考答案，为了后续叙述方便，特摘录如下（以下简称解法1）.

解法1：根据题意，不妨设刚出生时共有这种动物a只，则20年后存活的还有0.8a只，又过了5年还存活0.5a只，再过5年还剩0.3a只存活.

毫无疑问，上述题1与题2本质完全相同，据此，笔者斗胆猜测2016年厦门市中考命题专家就是从文1中的题2获得灵感，或者说就是模仿题2命制上述中考试题（即题1），因此2016年厦门市命题专家对于上述题1所给出的参考答案也就如同上述题2的解答过程，只不过具体数据稍作改变而已，即为：

三、质疑之声

中考结束，上述题1就招来质疑之声，质疑焦点主要集中在以下四个方面，其一，题1是条件概率吗？如果是，而初中没有学习条件概率，题1是否有超纲之嫌？其二，题1作为涉及千家万户的中考试题是否合适？其三，上述解法1是否正确？其四，如果解法1正确，那么命题专家给出上述解法1的理论依据是什么？

四、理性思考

俗话说得好：“解铃还须系铃人.”要释怀上述质疑，还要从高中的“条件概率”这一概念入手，方能解开谜团.

1.紧扣概念——条件概率原始定义

顾名思义，条件概率就是受到一定条件制约，也就是说，在一个事件发生的前提下，另一个事件发生的可能性大小.条件概率准确定义如下所示.（见文3第52页）.

定义：一般地，设A、B为两个事件，且P（A）＞0，则有

则称①为在事件A发生的条件下，事件B发生的条件概率.其中P（B A）读作A发生的条件下B发生的概率.

依据上述条件概率定义，上述题1与题2均属于条件概率，千真万确，没有任何争议，因此质疑超纲之嫌不足为奇，实属正常，这也说明中考后有人“雄辩”题1不是条件概率纯属“强词夺理”.让我们一起聆听文4中的“主编寄语”：“数学是清楚的.清楚的前提，清楚的推理，得出清楚的结论.数学中的命题，对就是对，错就是错，不存在丝毫的含糊.”

2.寻觅依据——条件概率计算公式

其实，上述条件概率定义本身（即上述①）就是计算条件概率的一个计算公式.对于古典概型（见文4）来说，若n（Ω）表示Ω中包含的基本事件所有结果个数，依据上述①得到：

特别地，

（1）当事件B包含于事件A，即B⊆A时，上述①还可以进一步得到：

（2）当事件B包含于事件A，即B⊆A时，上述②还可以进一步得到：

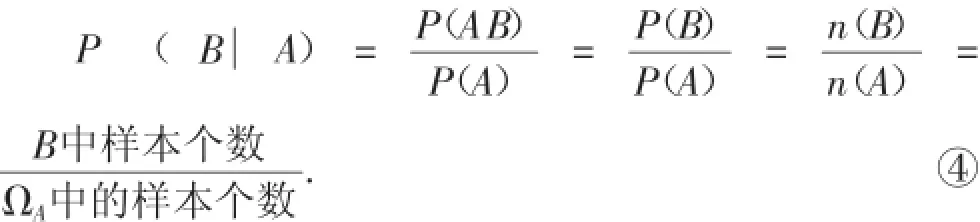
五、严谨推理

为了叙述方便与严谨，不妨设“活到20岁的这种动物”为事件A，则P（A）=0.8；设“活到25岁的这种动物”为事件B，则P（B）=0.6；“现年20岁的这种动物活到25岁”为事件C.依据题意得到B⊆A，依据上述公式③可得以下解法（以下简称解法2）.

上述解法2是高中常见的条件概率问题的解法，其理论依据就是条件概率定义及上述公式①、③.倘若依据上述公式④可得以下解答（以下简称解法3）.

六、心中疑惑

从上述条件概率定义及分析过程不难发现：文2及中考命题专家所给解答（即上述解法1）就是此处的解法3，即上述解法1就是解法3的“简略版”，因此可以肯定题1本身没有问题，解法1也是正确的.但是笔者还是有以下一些疑惑，在此向专家、同行请教.

1.能否随意删除前提

因为题1源自题2，题1与题2本质相同，因此不少读者根本没有察觉到题1与题2之间的细微差异，那就是文1中的题2的前提与背景，即第一句话“动物学家通过大量的调查估计”.然而中考命题专家在命制题1时却人为地删除了这句话，笔者认为这是败笔.题2之所以特意加上“动物学家通过大量的调查估计”，主编意在表明很多概率结论来自实践、调查及统计、估计，更在暗示初中没有涉及条件概率知识，其实是在为考生解决问题指明方向，即用频率估计概率，因此主编在文2第268页特意指出：“题2需要学生对用频率估计概率有更深层次的理解”，这正是主编给出上述解法1的缘由所在.基于初中仅仅接触概率基础知识，教科书（文1）甚至连“古典概型”这一名词都没有明确提起，更不要说几何概型了，因此文5明确指出：“知道通过大量的重复试验，可以用频率来估计概率.”为何初中特别重视借助频率估计概率呢？因为用频率来估计概率既不受试验结果个数是有限还是无限限制，也不受是否为等可能事件等限制，因此统计概率适用范围更广泛、更有效，这正好弥补了初中生认知水平不高及理解能力还不成熟而对深入理解相关概率问题带来的偏差.正因为题1删除了看似无关、实则关键的这句话，因此高中教师一致认同上述解法2、解法3而无法理解乃至质疑上述解法1.一个非常有趣的现象：对于上述题1，笔者先后咨询多位初中教师，几乎异口同声地说：“很简单，直接相除”（注：此处的“相除”就是指解法1），而高中、大学教师首先想到的是这是条件概率，应该利用上述①或②解决.

2.试题是否有超纲之嫌

由上述详细分析过程与结果足以说明：文2与命题专家解答的理论依据就是条件概率的定义及上述公式④，而且还利用了一个重要概念，即事件包含关系：B⊆A.这些知识与概念确实属于高中范畴，可以明确地说，没有条件概率定义，没有事件包含关系是不可能得到上述解法1的.也就是说，文2及中考命题专家所给解法1就是在默认“已知条件概率及事件包含关系”的前提下而得到的.而初中既没有学习条件概率定义，也没有学习事件包含关系，因此上述题1及解法1确有超纲之嫌，毋庸置疑.

3.作为中考试题是否恰当

中考涉及千家万户切身利益，事关莘莘学子升学择校，因此命制中考试题应该慎之又慎.不仅要从考查难度上控制，还要从考查内容上把握，特别要遵循《义务教育数学课程标准》（文5）、考纲及本地区的实际情况来命制试题.

俗话说：“打灯笼照旧.”因此不少人认为，题1源自文1中的题2，既然文1已经出现题2，为什么说题1有超纲之嫌？事实上，题2既不是作为教科书的一个例题，也不是作为一个普通习题，而是安排在教科书的“拓广探索”栏目，充分说明教科书主编已经考虑到题2的难度、深度与广度，其目的就是为了开阔学生视野、优化学生思维，为教师及能力较强的学生而设置，因此这个栏目的名字“拓广探索”本身就包含着“拓展、引申、探究”等更深层次的目标，更何况主编在文2（教师教学用书）第268页特意指出：“题2有一定难度”，这足以说明教科书主编在警醒一线教师应该有选择性地妥善处理题2，而不是千篇一律地要求所有学生掌握.笔者在第一时间特意就题1请教不少专家、学者，得到回复基本都是“这真的是中考试题吗？”“对于初中学生，这也太难了.”……事实胜于雄辩，中考阅卷之后的统计数据表明此题得分率极低，这也从一个侧面说明题1并非完美.综上所述，笔者认为将题1作为中考试题不是很恰当，值得专家、学者们进一步商榷.

七、几点建议

笔者爱好将各地中考（当然也包括高考）试题做一遍，不时发现个别试题有超纲之嫌、有概念不清之处、有不严谨之处.要想避免命制试题之中出现瑕疵乃至错误，关键在于命题专家把好命题关，严格按照流程操作，丝毫不放过任何一个环节，哪怕一丝一毫也要慎之又慎.除此之外，还需要主管部门在选拔命题专家时适当关注命题组成员的搭配，这一点非常重要.只有命题组成员明晰初中数学概念，同时包括高中数学概念，甚至还要准确把握小学及大学数学概念才能命制出一份紧扣教材、洞察概念、面向全体、范围恰当、难度适中的高质量试题.

1.成员搭配

目前各省市中考试题命题工作主要由初中一线教师及教研部门的教研员组成，这无可厚非.笔者认为还要适当选拔具有丰富教学经验、概念把握极其精准的高中一线教师参加命题，这样既能保证中考命题有利于考生后续高中学习，更能有效避免范围超纲等不必要瑕疵.像上述题1，如果命题组中有功力深厚的高中数学教师，应该立即就能发现题1属于条件概率.也许有人质疑笔者看轻初中教师，甚至贬低初中教师水平，笔者绝无此意.因为能够参加中考命题的教师都是鼎鼎有名的初中教师和资深教研员，而能够成为一个地区乃至一个省家喻户晓的名师一定经历了较长的教学生涯磨练，因此这些名师相对年龄较大，也就是说，尽管他们功力深厚，但毕竟远离高中数学多年，加上高中数学教科书多次变化，甚至不少内容进行了增加与删除，他们未必及时知晓.还有目前我国中小学教学模式分为小学、初中和高中，逐步形成“铁路警察各管一段”的局面，因此初中教师不太了解高中数学课程与内容，在此笔者呼吁中考命题组成员中至少应该选拔一名对高中数学概念精通的教师与初中教师及教研员一起共同完成中考命题，就像高考命题专家之中一定要配置大学教授或科研部门专家一样，其目的就是为了把把关、摸摸脉，预防出现本应完全可以避免的瑕疵与错误.

2.顾全大局

中考命题既要有利于初中教学，同时还要顾及高中乃至大学学习.如果说高考是为高校选拔优秀高中毕业生进一步深造，那么中考就是为了进入高中继续学习而进行的全面性检测考试，因此中考试题应该面向全体考生，难度应该适中，知识点应该较为全面.随着2016年回归全国统一高考命题，不少省份也正在实施或正在酝酿中考全省统一命题，可以集全省之力、聚全省名师命制试题，这样质量更高，更为重要的是与高考回归全国统一命题大背景保持一致，为初中教学指明方向，实现初高中教学的衔接，逐步打破初高中教学断层的局面.

3.优先概念

中考命题也好，高考命题也罢，其实衡量一份试卷质量高低、考量一道试题是否恰当、核准一道试题是否超纲，关键在于是否吃透概念，核心在于知晓概念来龙去脉.近年来笔者重视数学概念及概念教学，尤其在承担全国课题“基于数学教学内容知识（MPCK）视角下的概念教学案例研究”研究之后，更是特别关注数学概念与中考、高考命题之间的紧密联系并取得一点点收获，陆续发表了文6～8，其中文6、文7是针对目前高考命题与中学及大学概念之间的关联；文8则是跨越小学、初中、高中及大学概念之间的千丝万缕的联系.本文通过一道中考试题的质疑之声及理清之路，渴望更多一线教师不仅在教学之中，而且在命题之时都要关注数学概念，尤其是数学核心概念（比如函数、统计、概率等），这是数学教学的根本出发点，也是中考、高考命题依据所在.

行文结束，再次强调这是笔者一点心得体会，绝没有贬低更没有攻击命题专家之意，这正是文中没有用“某某市中考试题”来替代的原因，本文纯属从学术视角进行探究，不当之处，敬请批评指正，万分感谢.

1.义务教育教科书数学九年级（上册）［M］.北京：人民教育出版社，2015.

2.义务教育教科书数学九年级（上册）教师教学用书［M］.北京：人民教育出版社，2015.

3.普通高中课程标准实验教科书数学选修2—3（A版）［M］.北京：人民教育出版社，2012.

4.普通高中课程标准实验教科书数学必修3（A版）［M］.北京：人民教育出版社，2012.

5.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

6.王淼生.疑虑与渴望［J］.中学数学（上），2014（5）.

7.王淼生.2014年全国高考福建卷数学理科第21题的赏析［J］.数学教学，2014（12）.

8.王淼生.基于MPCK视角下的概念解读——以凸多边形内角和为例［J］.中学数学（下），2016（7）.Z

*本文系全国教育科学“十二五”规划2015年度单位资助教育部规划课题“基于数学教学内容知识（MPCK）视角下的概念教学案例研究”（课题批准号：FHB150464）的研究成果.