从“形聚”到“神似”:大题命制的一种追求——2016年盐城卷第28题思路突破与命题反思
2016-12-07江苏省张家港市塘桥初级中学王东
☉江苏省张家港市塘桥初级中学王东
从“形聚”到“神似”:大题命制的一种追求——2016年盐城卷第28题思路突破与命题反思
☉江苏省张家港市塘桥初级中学王东
承载着中考区分选拔功能的压轴题往往倍受大家关注.有些考题呈现简约、渐次生长、前后关联、上下呼应等特征,给练习者、欣赏者以美的享受.然而也有些综合题把几个无甚关联的小问题勉强拼凑成一道大题,让练习者感觉是在练习一大堆不相关的题目.本文关注一道中考压轴题,尝试给出思路突破和解后反思,并改编变式,提供研讨.
一、考题及思路突破
考题(2016年江苏盐城中考数学卷第28题)如图1,已知一次函数y=x+3的图像与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c过A、B两点,且与x轴交于另一点C.
(1)求b,c的值.
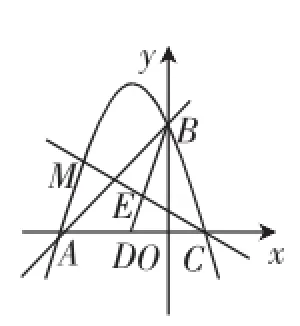
图1
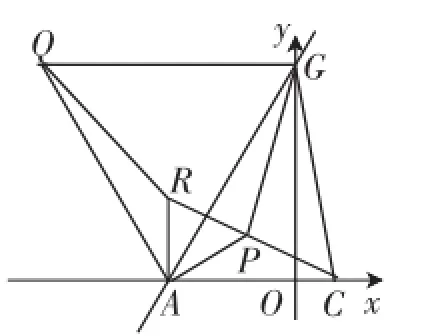
图2
(2)如图1,D为AC的中点,点E在线段BD上,且BE= 2ED,连接CE并延长交抛物线于点M,求点M的坐标.线CE与抛物线解析式,可得M点坐标为(-,).是一个含60°角的特殊直角三角形,G(0,3),AG=6.以AG为边向左侧作等边△AGQ,可求出Q点坐标为(-6,3).有了这些解读之后,可以进入后续问题的
(3)首先解读一些初始条件,比如,将直线AB旋转后得到直线AG的位置,应该是与x轴成60°角,即△AOG求解了.
①根据两个等边三角形的条件,加上∠GAO=60°的识别,容易证明△ARQ≌△APG,从而得到PG=RQ;
②认真观察图2,发现由上一问中△ARQ≌△APG,有PG=QR,要想PA+PC+PG取得最小值,就是PR+PC+QR取得最小值,只要四点C、P、R、Q共线即可,即最小值就是连接QC,求线段QC的长,这两个端点的坐标都是明确的,构造图3,很快可求得QC=2
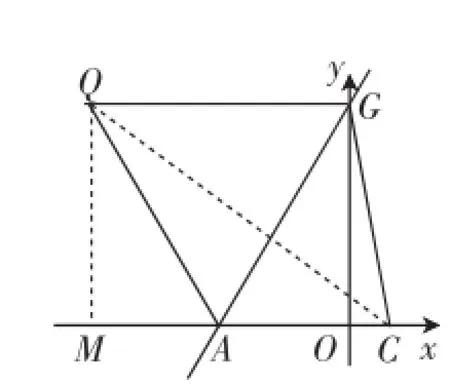
图3
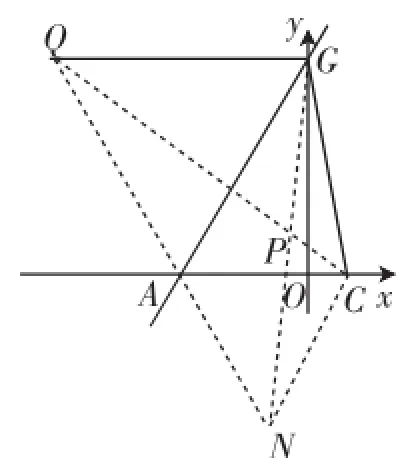
图4
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG.如图2,P为△ACG内一点,连接PA,PC,PG,分别以AP、AG为边在它们的左侧作等边△APR、等边△AGQ,连接QR.
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.
1.思路突破
(1)由一次函数解析式可确定A、B点的坐标,再将其代入抛物线解析式就能确定b、c的值,即b=-2,c=3.
(2)由上一问求出的抛物线解析式,可以求出C点坐标为(1,0),容易解读点D的坐标为(-1,0),再由BE= 2ED,可求出点E的坐标为(-,1);于是根据待定系数法可以确定直线CE的解析式为y=-x+,进而联立直
到此进展都很顺利,真正的挑战是点P的位置,即如何求点P的坐标.
我们很快会确认点P应该在线段CP上,但是具体位置呢?如果有“费马点”的模式积累的话,可以构造图4解决,以AC为边向下作等边△ACN,连接CQ,GN交于P点,该点为△ACG的费马点,满足AP+CP+GP最小,这样可以求出直线CQ的解析式为,直线GN的解析式为,再联立方程组解出点P的坐标为
然而,上述解法的难点在于“以AC为边向下作等边△ACN”,这种构造如果缺少对三角形费马点的深刻理解,短时间是难以获得思路的,而且费马点也并非是初中阶段的教学要求.让我们另寻突破点P坐标的思路.
考虑到△APR是等边三角形,可以作AH⊥CQ于H点,根据相似三角形性质(△ACH∽△QCM)或锐角三角函数(∠ACQ的三角函数值)可以求出换到Rt△APH中,可求出
由于三个小问之间基本无甚关联,特别是第(3)问甚至离开总题干中的抛物线,另起炉灶,命题者“引来”了所谓的费马点问题,让难点落在最后一问上.以下再简述几处障碍点:
障碍点之一:缺少费马点结构的认识,难以获得最值.
如果缺少费马点的结构,则短时间学生认识到线段CQ就是最小值有些障碍,就是想到连接CQ,也并不一定能认识到这就是三条线段和的最小值.
障碍点之二:构造出图5之后在不同的三角中切换不畅,导致思路受阻.
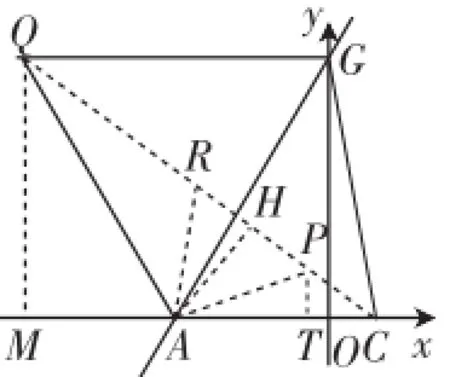
图5
图5中需要灵活的目光转换能力,如果不能有效、按序转换,则往往思路受阻.特别是求解的次序:先求AH→PH→HC→PC→PT→CT.这一路径如果走偏,则会消耗时间成本.
障碍点之三:运算繁杂,对运算的意味品质有较高的要求.
由于涉及的三角形三边之间不是学生熟悉的特殊三角形,所以无论是相似路径,或是锐角三角形函数路径,都会陷入较为繁杂的运算.笔者经过演算,发现有些相似的路径虽然思路是通的,但是构造出来的一元二次方程计算非常繁杂,只得放弃.
二、关于综合题命题的一些思考
1.综合题的系列小问尽量“看似并列,实质递进”
就笔者认真研习全国各地中考试卷,特别是北京、上海等省会城市的中考试题最后一问,往往都是在一个题干之下系列生长出来的题组,往往“看似并列,实质递进”,即看上去几个小问之间并列式设计,互相条件不能混用,但是前问的解法、思路却对后问的思考探究起着暗示、铺垫的作用.而上文中考题的三个小问,特别是第(3)问与前面两个小问基本缺少关联,甚至让题干也“提前枯萎”,似有遗憾和不足.
2.综合题的命题导向重在“考查思维,淡化运算”
由于目前各地中考题的题量偏大,答题时间偏紧,如果在最后一道大题仍然有较大的运算量,特别是繁杂运算时,往往会影响试题考查的重要追求,即数学试题应该重在考查数学思维,而淡化运算.像上面的解法中,涉及很多分数、无理数系数的函数表达式,或线段的长都带分数、无理数,且三角形三边关系也不是学生熟悉的常见特殊三角形,使得学生尽管知道问题的思路,但是由于运算量繁杂而思路受阻,让一些放弃最后大题的学生与认真思考的学生得分相近,使得该题的信度、效度都大打折扣.
3.综合题中蕴含的问题结构尽量不涉及高中内容
作为中考毕业、升学合一的考试,首先应该严守数学课程标准,不得“超标”,或者不得打擦边球.最后一问隐含着费马点模型,让很多应试复习中通过题海战术或补充过费马点的学校与考生就能一眼洞察问题结构,造成命题背景上的不公平,这是值得命题者思考的.想起,前几天有些地区的最后一道隐含着高中阶段的抛物线的准线、焦点问题,带来了相应地区在中考应试复习时以准线、焦点为专题的复习课研讨,实在是“上有所好,下必趋之”.
三、变式研讨
与教学一样,命题也是一项充满遗憾的艺术.知易行难,以下本着个人命题研究的兴趣,给出笔者的一种变式改编题,提供批评.
变式改编题如图6,已知一次函数y=x+3的图像与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c过A、B两点,且与x轴交于另一点C.点M是抛物线在第二象限上的一点,直线MC,AB相交于点N.
(1)求b,c的值;
(2)当N恰为线段AB的中点时,求点M的坐标;
(3)连接AM,BM,当△ABM的面积取得最大值时,求线段MN的长.
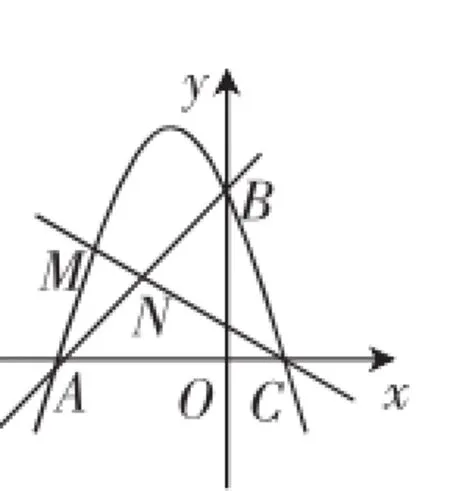
图6
1.何明.由博返约,追求简洁——一道“双曲线”综合题的命题过程[J].中学数学(下),2015(11).
2.刘东升.“并列”式问题与“递进”式求解——由一则解题教学案例说起[J].中学数学教学参考(中),2012(8).
3.夏盛亮.引导回归教材,倡导开放取向——一次县级期末卷的命题取向分析[J].中学数学(下),2014(1).
4.鲍建生,顾泠沅,等.变式教学研究[J].数学教学,2003(1,2,3).H
