快速自适应经验模态分解方法及轴承故障诊断

2016-12-07李富才李鸿光

振动、测试与诊断 2016年4期

关键词：本征包络线端点

陈凯，李富才，李鸿光

(上海交通大学机械系统与振动国家重点实验室上海，200240)

快速自适应经验模态分解方法及轴承故障诊断

陈凯，李富才，李鸿光

(上海交通大学机械系统与振动国家重点实验室上海，200240)

提出一种快速自适应经验模态分解(fast and adaptive empirical mode decomposition ,简称FAEMD)，其算法结构和本征模态函数的特点与经验模态分解(empirical mode decomposition, 简称EMD)类似。采用顺序统计滤波器代替三次样条来拟合曲线，简易的终止准则使耗机时间大幅减小。该方法可以快速、有效、准确地分解信号，能够避免终止准则和端点效应问题，改善模态混叠和耗时问题。在滚动轴承故障诊断的应用中，效果表现良好。

经验模态分解；快速自适应经验模态分解；滚动轴承；顺序统计滤波器

引言

时频分析方法适合用于非平稳信号，包含Wigner-Ville分布、小波变换、短时傅里叶变换和Hilbert-Huang变换等，其中前3种方法存在自适应性缺陷。经验模态分解[1]是Hilbert-Huang变换的核心部分，它是一种具有自适应性的时频分析方法，适合对非平稳信号进行分析。于德介等[2]把EMD引入旋转机械故障诊断领域。针对EMD的模式混叠缺陷，文献[3]利用白噪声的频率均匀分布统计特性提出集合经验模态分解(ensemble empirical mode decomposition,简称EEMD) 。景蓓蓓[4]对微分的经验模态分解(differential-based empirical mode decomposition,简称DEMD)进行实验验证，得出EDMD和EEMD相对传统方法EMD耗机时间大幅度增加。EEMD，EMD运算耗时的缺点限制了其在旋转机械在线监测与故障诊断中的应用。为了提高EMD的运算效率，比如减少取样[5]，但还是无法避免EMD本身的缺陷。

针对文献[6-7]对二维经验模态分解法进行改进提出的算法，笔者构造了一维快速自适应经验模态分解法。算法采用顺序统计滤波器代替三次样条来获取上下包络线，省去了复杂的终止准则。结果表明，算法效率显著提高，EMD的传统缺陷得到避免,将该算法应用到滚动轴承故障诊断效果良好。

1 FAEMD理论

1.1 FAEMD本征模态函数的特点

FAEMD方法的本质与EMD是一样的，将一个信号分解为有限个本征模态函数，每个本征模态函数为信号的一个单分量信号，必须满足两个条件：a.在整个信号长度范围内，极值点和过零点的数目必须相等或至多相差一个；b.信号上任何一点，由局部极大值确定的上包络线和局部极小值确定的下包络线的平均值始终为零，或接近零。实际上，第1个条件相当于稳态高斯分布的窄带信号条件, 起到排除骑行波的作用；第2个条件是把对信号的全局约束修改为局部约束。这种限定的好处是可以减少在信号处理过程中由于波形不对称所产生的瞬时频率扭曲现象[8]。

1.2 顺序统计滤波器和包络线

在EMD算法中，普遍使用三次样条插值的办法获取上下包络。这里采用顺序统计滤波器(order statistics filter, 简称OSF)替代，不仅节省计算耗机时间，还在许多指标上表现出色。一阶顺序统计滤波器对信号做如下处理：假设输入信号为{Xi}，输出为{Yi}，窗口尺寸为L=2w+1。其中：L为滤波器的长度；w为原始信号中相邻极大值点的最小间距。

顺序统计滤波表示为

(1)

bi为滤波器特性，即

(2)

Yi取的是L这一段内的极大值，具体算法见文献[9]。

图1为仿真信号的上下包络线的求取过程，其仿真信号为一个序列信号

z=sin(2π4t)+3sin(2π8t)

(3)

上下平滑曲线即为包络线，中间幅值最小的曲线为包络线的均值曲线。包络均值曲线在某些地方不平滑，存在一阶不可导点，采用加窗平滑处理。一般采用均值形式做平滑处理，如式(4)对数据点前后r个数据求和再做平均。

图1 上下包络和均值滤波示意图Fig.1 Upper & lower envelope and smooth mean envelop

(4)

1.3 FAEMD计算步骤

将原始信号设为I，快速EMD分解的本征模态函数设为F，余量设为R，其计算步骤如下。

1) 定义 Si=I,i=1,2,…。

2) 获取Si的极大值序列，定义为Pi序列，其值为信号的极大值点的横坐标值序列。

3) 采用顺序统计滤波器，计算Pi序列中最小相邻极值点间距w，以(2w+1)为滤波器的长度，获取Pi的包络线，定义为上包络线UE。

4) 获取Si的极小值序列，定义为Qi序列，其值为信号的极小值点的横坐标值序列。

5) 采用顺序统计滤波器，计算Qi序列中最小相邻极值点间距w，以(2w+1)为滤波器的长度，获取Qi的包络线，定义为下包络线LE。

6) 求上下包络线的平均值MEi=(UE+LE)/2。

7) 采用均值形式对包络均值做平滑处理

MEi=smooth(MEi)

8) 计算Fi=Si-MEi;i=i+1;Si=MEi-1，其中Fi为第i次分解的本征模态函数。

9) 终止条件：当I大于信号长度的1/3，或极值点数小于3，或超过设定的本征模态函数的个数; 否则，重复步骤1～9。

10) 当余量R=Si，分解终止。

按照计算步骤分解之后得到多个本征模态函数和余量

(5)

其中: N为本征模态函数的个数，说明FAEMD满足完备性。

FAEMD算法流程如图2所示。

图2 FAEMD算法流程图Fig.2 The algorithm flow chart of FAEMD

2 FAEMD相关问题

2.1 端点效应

传统EMD算法中，端点效应主要来自样条拟合过程，尤其在处理长度较短的信号中。主要是在信号的两端，由于无法获取足够的极值点导致信号拟合出现误差甚至在信号两端出现发散现象[10]，且这种误差会不断地延续到下一个本征模态函数中。

很多学者针对端点效应做了研究[11-12]。在FAEMD算法中，上下包络线通过顺序统计滤波器拟合，在边界处的处理不需要多个极值点信息，效果在两端同样得到保证，从而避免端点效应。从图1可以看出，包络线在两端点处于收敛状态。

2.2 耗机时间

在传统EMD算法中，采用三次样条拟合的办法获取上下包络线，这个过程是消耗时间的主要部分，而且信号成分越复杂，耗机时间将越久。为了达到效果并满足本征模态函数的条件，往往每次分解都需要循环若干次，导致时间成本增加。在EEMD算法中，利用白噪声的频率均匀分布统计特性，多次分解用均值的形式表示本征模态函数，最大缺点为耗机时间成百倍的增加。

FAEMD算法采用顺序统计滤波器，根据极值点集获取上下包络线，这个过程能被计算机快速处理，包络线的均值过程同样可以快速处理。

2.3 模态混叠现象

在EMD中，模态混叠现象非常常见[13]。FAEMD能够减少模态混叠现象，主要是由顺序统计滤波器的窗口长度决定的。当信号中高频成分存在时，窗口非常小，用小窗口获取信号的上下包络线，较好地描绘了低频信号，使其保留在下次分解中，高频信号则被分离出来。图3表明了FAEMD在混叠效应中的优势。图3(a)包含两个明显的低频和高频成份，此时滤波器的窗口较小，包络线和包络均值曲线都很好地刻画了低频成分，原始信号减去包络均值得到高频信号。被分解出来的高频信号和保留的低频信号如图3(b)所示。包络均值在高频信号的边界处有一些凹凸的地方，产生了一些偏差，不过这些偏差在下一次分解中很容易被分解出来。

图3 FAEMD的分解过程Fig.3 Decomposition process diagram of FAEMD

3 仿真信号分析

构造了一个信号，由3个频率成分组成，即正弦信号、非平稳信号和线性信号。S1，S2和S3构成分析信号S。采样点数为1 280，采样频率为1 kHz，幅值大小如图4所示。

图5为采用传统EMD算法分析结果。筛分准则选取SD=0.3，最大循环设为50，共分解出4层信号。Res代表剩余的信号即趋势项。其中，IMF1和IMF3与原始信号中的S2和S1两个频率信号相似，但是差异很大且余项Res端点错位严重。IMF2为分解IMF1时泄漏出来的部分，幅值较小因而能量不大。

图4 原始信号及信号成分Fig.4 The original signal and the signal component

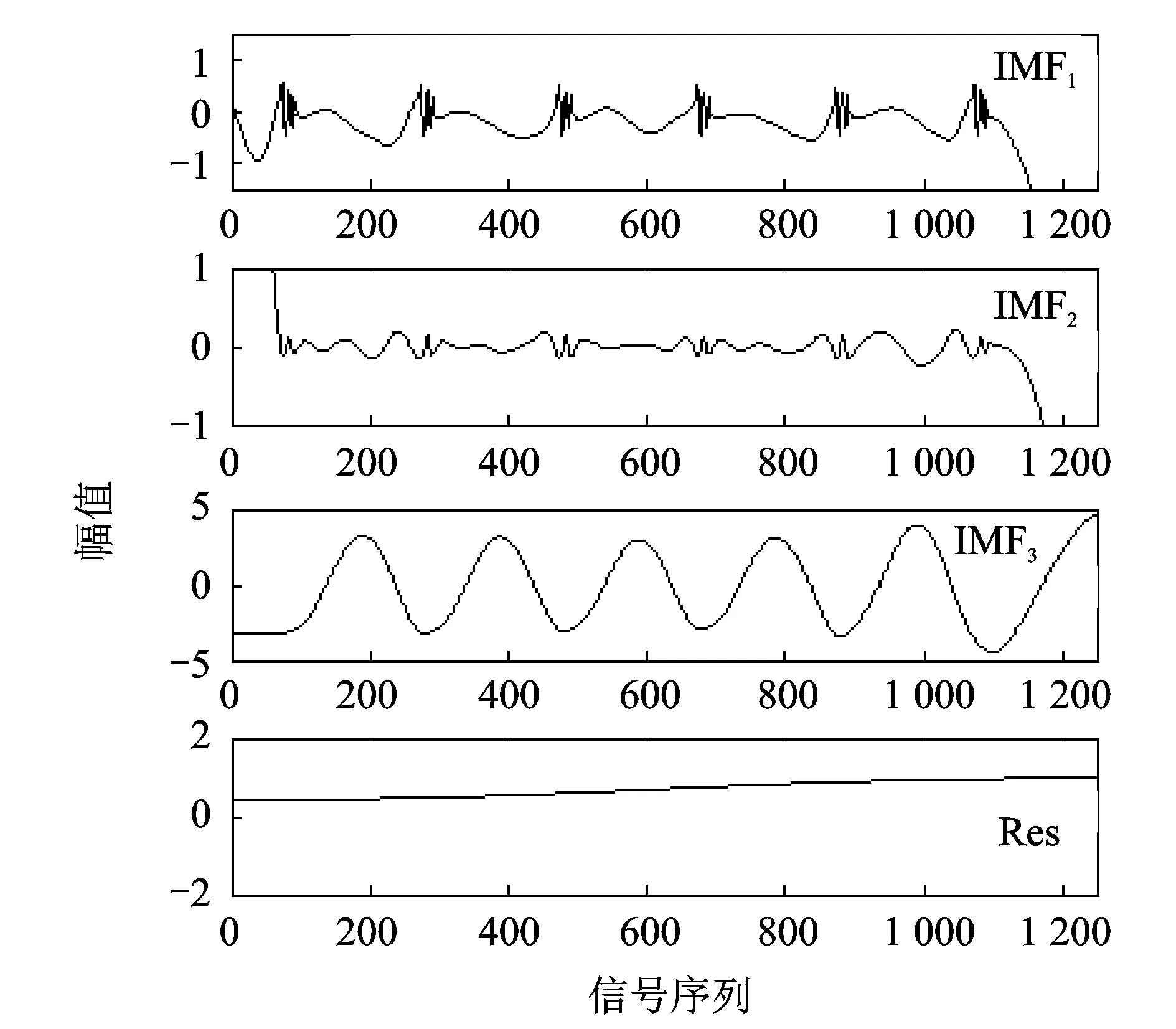
图5 采用镜像延拓技术的EMD分析结果Fig.5 The result of EMD using mirror continuation

图6为采用FAEMD算法分析结果。同样，在端点处加入镜像延拓进行显示对比，共分解出FIMF1，FIMF2和余项Res。其中，FIMF1，Res相比原始信号的S3和S1有轻微差别，但比EMD算法的分解效果要好，且没有多余的无效分解信号，余项Res的端点没有错位，保持了原有的物理含义。

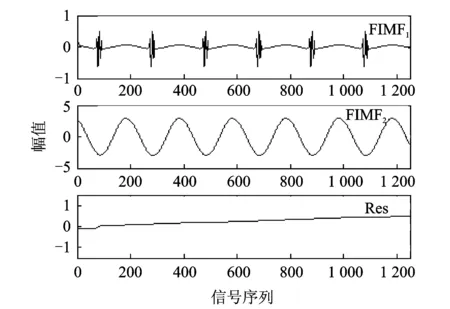
图6 采用镜像延拓的FAEMD分析结果Fig.6 The result of FAEMD using mirror continuation

表1为两种算法的耗机时间，同时添加高斯白噪声，使分析信号的成分变复杂，来模拟现实环境并计算其耗机时间。由于仿真信号比较简单，所以EMD算法的耗机时间较短，但添加白噪声后EMD耗机时间增加一半多，而FAEMD的耗机时间基本不变。

表1 EMD和FAEMD算法的耗机时间

Tab.1 Time consumption of EMD and FAEMD s

4 实例分析

本实验采用美国西储大学驱动端轴承内圈故障信号数据。采样频率为12 kHz，数据点数为6 144。数据分析前对数据重采样，采样频率设为6 kHz。滚动轴承型号为6205-2RS JEMSK，滚珠为9个，内径为25 mm，外径为51.998 88 mm，球直径为7.940 04 mm，节圆直径为39.039 8 mm，转子转速为1 730 r/min，计算得出内圈故障特征频率为156.2 Hz。原始信号经FAEMD分解，得到各本征模态函数。对每个本征模态函数进行傅里叶变换，查看其频率成分。

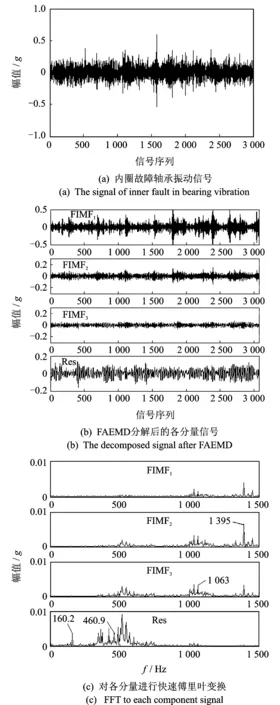
图7 轴承内圈故障诊断Fig.7 Diagnose of inner fault in bearing

图7(a)为带内圈故障的滚动轴承原始信号，信号成分非常复杂，很难直接看出故障信号。图7(b)为FAEMD的各本征模态函数和余量，总数设为4个。对每个分量进行傅里叶变换，如图7(c)所示。Res中160.2 Hz,460.9 Hz信号与内圈故障特征频率及三倍频非常吻合。FIMF3和FIMF2中1 063 Hz和1 395 Hz信号与内圈故障特征频率的七倍频率和九倍频非常吻合,其误差都属于正常范围，说明内圈故障存在。很多学者基于EMD的滚动轴承故障诊断做了研究[14]，而FAEMD算法实质上是一样的，因而在滚动轴承中应用同样非常广泛。基于FAEMD算法的快速性，非常适用于旋转机械在线监测与故障诊断中。

5 结论

1) 构造了一种快速经验模态分解的算法，能够快速有效地对信号进行分解处理, 同时在端点效应、耗机时间和模态混叠的问题上有较好的改进。

2) 仿真信号和实验信号证明了FAEMD算法的可靠性和快速性。滚动轴承故障信号分析表明，FAEMD算法能很好地提取出故障信息。

3) 基于FAEMD算法的快速性，对一些在线监测诊断系统有很大的帮助。

[1] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[2] 于德介，程军圣. EMD方法在齿轮故障诊断中的应用[J]. 湖南大学学报:自然科学版, 2002(6):48-51.

Yu Dejie, Cheng Junsheng. Application of empirical mode decomposition method to gear fault diagnosis [J].Journal of Hunan University: Natural Science Edition, 2002(6):48-51. (in Chinese)

[3] Wu Z, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Mathematical, Physical and Engineering Sciences, 2004, 460(2046): 1597-1611.

[4] 景蓓蓓. 基于微分的经验模态分解及其在多重转子故障分析中的应用[D]. 上海：上海交通大学，2009.

[5] 吴顺德, 陈良荣, 吴求文, 等. 以减少取样來提升经验模态分解演算法计算效率之研究[J]. 资讯科技国际期刊，2010，4(1): 56-70.

Wu Shunde, Chen Liangrong, Wu Qiuwen, et al. To reduce the sampling to promote empirical mode decomposition algorithm of computing efficiency research[J]. International Journal of Information Technology, 2010, 4(1): 56-70. (in Chinese)

[6] Bhuiyan S M A, Adhami R R，Khan J F. Fast and adaptive bidimensional empirical mode decomposition using order-statistics filter based envelope estimation[J]. Eurasipe Journal on Advances in Signal Processing, 2008 (2008): 164.

[7] Bhuiyan S M A, Adhami R R，Khan J F. A novel approach of fast and adaptive bidimensional empirical mode decompositon[C]∥2008 IEEE International Conference on Acoustics, Speech and Signal Processing. Las Vegas: [s.n.], 2008: 1313-1316.

[8] 金辉. 基于EMD的语音信号检测与增强方法研究[D]. 哈尔滨: 哈尔滨工程大学，2012.

[9] Ramirze J, Segura J C, Benitez C, et al. An effctive subband OSF-based VAD with noise reduction for robust speech recognition[J]. Transaction on Speech and Audio Processing, 2005, 13(6):1119-1129.

[10]程军圣, 于德介, 杨宇. Hilbert-Huang 变换端点效应问题的探讨[J]. 振动与冲击，2005，24(6):40-42.

Cheng Junsheng, Yu Dejie, Yang Yu. Discussion of end effects in Hilbert-Huang transform[J]. Journal of Vibration and Shock, 2005,24(6):40-42. (in Chinese)

[11]王学敏, 黄方林. EMD端点效应抑制的一种实用方法[J]. 振动、测试与诊断, 2012, 32(3): 493-497.

Wang Xuemin, Huang Fanglin. Practical method to restrain the end effect of EMD[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(3): 493-497. (in Chinese)

[12]Yao G, Zhao J J, Yao Y T, et al. Separation of systematic error based on improved EMD method[J]. Journal of Vibration and Shock, 2014, 33(14): 176-180.

[13]Colominas M A, Schlotthauer G, Torres M E. Improved complete ensemble EMD: a suitable tool for biomedical signal processing[J]. Biomedical Signal Processing and Control, 2014，14(1):19-29.

[14]张志刚, 石晓辉, 施全, 等. 基于改进EMD和谱峭度法滚动轴承股长特征提取[J]. 振动、测试与诊断, 2013, 33(3): 478-482.

Zhang Zhigang, Shi Xiaohui, Shi Quan, et al. Fault feature extraction of rolling element bearing based on improved EMD and spectral kurtosis[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3): 478-482. (in Chinese)