电梯系统垂直振动的频率敏感度分析与鲁棒设计

2016-12-07冯文周曹树谦

振动、测试与诊断 2016年4期

关键词：轿厢共振固有频率

冯文周，曹树谦，胡铖

(1.天津大学机械工程学院天津，300072) (2.天津市非线性动力学与混沌控制重点实验室天津，300072) (3.大连理工大学机械工程学院大连，116024)

电梯系统垂直振动的频率敏感度分析与鲁棒设计

冯文周1，2，曹树谦1，2，胡铖3

(1.天津大学机械工程学院天津，300072) (2.天津市非线性动力学与混沌控制重点实验室天津，300072) (3.大连理工大学机械工程学院大连，116024)

考虑曳引绳刚度在电梯运行过程中具有变刚度的特性，利用Lagrange方程对电梯系统建立了7自由度的振动微分方程，通过试验设计方法得出随机变量与系统频率响应的数值关系，利用人工神经网络技术获得随机变量与频率响应之间的显性函数关系式。根据激振频率与固有频率之比不超过规定值的关系准则，定义了电梯系统纵向振动的可靠性模式，运用频率可靠性分析方法，提出多频激励情况下的系统的频率可靠性及其敏感度的分析方法。在此基础上，结合可靠性敏感度理论与稳健设计方法，将可靠性敏感度融入到目标优化设计中，建立系统频率可靠性鲁棒设计模型。通过工程算例，将可靠性敏感度理论和稳健设计方法应用到电梯系统设计当中，得到满足鲁棒设计要求的随机参数值。结果表明，该方法具有较高的计算效率和求解精度，可以作为电梯系统稳健设计的理论依据。

电梯系统；频率共振；神经网络；频率可靠性敏感度；鲁棒设计

引言

电梯作为机电产品的一个有机体，其振动特性受到机-电两方面因素的影响，其动态特性较为复杂[1-3]。由于各部件的加工精度和安装误差等因素，电梯系统在运行过程中存在多个激振力。当激振力的频率与电梯系统的某阶固有频率较近时，会导致电梯系统共振，引起轿厢振动强烈，严重影响电梯运行质量。电梯由设计不当而导致系统共振，是电梯振动超标的主要原因之一。目前，国内外学者对于电梯系统振动特性的理论研究也取得了一些成果[4-7],但对电梯系统可靠性敏感度分析和可靠性稳健设计方面的研究较少。通过可靠性敏感度分析得到系统设计参数的变化对系统可靠度的敏感度，基于可靠性敏感度的分析对系统进行可靠性鲁棒设计，可以使系统具有较高的可靠度和鲁棒性，以达到稳健设计的目的。

笔者在频率可靠性研究的基础上[8-11]，定义了多频激励条件下的共振失效模式，给出了在串联系统共振失效模式的可靠度和可靠性敏感度计算方法。将可靠性敏感度理论与稳健设计方法相结合，针对工程实例，对电梯系统频率可靠性敏感度分析和稳健设计进行了研究。

1 电梯系统纵向振动微分方程

电梯的机械系统主要由轿厢、对重、悬挂装置、曳引机和曳引绳等子系统组成。本研究对象为无机房曳引式电梯，将其等效为7自由度的动力学模型，如图1所示。模型中：m1，m2，m3和m4分别为对重装置、曳引机、轿厢反绳轮和轿厢的等效质量；J1，r1分别为对重反绳轮的转动惯量和回转半径；J2，r2分别为曳引轮的转动惯量和回转半径；J3，r3分别为轿厢侧反绳轮的转动惯量和回转半径；k1，c1分别为对重侧绳头弹簧的刚度和阻尼；k2，c2分别为曳引机隔振垫的等效刚度和阻尼；k3，c3分别为轿厢侧绳头弹簧的刚度和阻尼；k4，c4分别为轿厢与反绳轮之间隔振垫的刚度和阻尼；k5，k5*，c5和c5*分别为对重两侧曳引绳的等效刚度和阻尼；k6，k6*，c6和c6*分别为轿厢两侧曳引绳的等效刚度和阻尼。

图1 电梯系统动力学模型Fig.1 Dynamics model of elevator system

根据Lagrange方程得到系统的振动微分方程为

(1)

T，U分别为

(2)

(3)

其中：x1，x2，x3，x4分别为m1，m2，m3，m4的线位移，

垂直向上为正；θ1，θ2，θ3分别为m1，m2，m3的角位移，逆时针方向转动为正；k5，k5*，k6，k6*的刚度与轿厢所处的位置有关；k11，c11分别为对重左侧曳引绳与绳头弹簧的的串联刚度和阻尼；k33，c33为轿厢右侧曳引绳与绳头弹簧的串联刚度和串联阻尼。

(4)

(5)

(6)

(7)

其中：N，E，A分别为曳引绳的个数、弹性模量和截面面积；H为提升高度。

将式(2)～(7)代入式(1)，得到系统振动的微分方程,写成矩阵形式为

(8)

其中：X={x1, x2, x3, x4, θ1,θ2,θ3}T为系统的位移向量；M，K，C分别为系统的质量矩阵、刚度矩阵和阻尼矩阵。

2 电梯系统共振的可靠性分析

由离散结构体组成的系统发生共振时，各结构体的振幅均达到最大。当结构体的振幅超过槛值，则结构系统处于失效状态或准失效状态。根据激振频率与系统固有频率的关系准则，定义电梯系统共振失效的状态函数为

(9)

其中：fi为系统的激振频率；f1，f2分别为由曳引机驱动轮、轿厢反绳轮产生的激振频率；ωj为系统的j阶固有频率。

根据激振频率和系统固有频率的关系准则，可以确定结构发生共振失效的极限状态函数。

(10)

其中：λ为一特定的值，工程上一般取10%～15%。

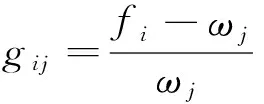
(11)

一般情况下，系统结构的随机参数分布服从某种类型。如果想精确获得系统随机参数的实际分布类型，就需要大量的试验数据进行统计学分析，这给分析带来了困难。在工程实际中，随机变量以正态分布最为典型，这也是在工程分析中首选的分布类型。假定系统随机参数服从正态分布，则系统共振失效的概率为

(12)

其中：Φ(·)为标准的正态分布。

μgij和σgij分别为gij的均值和标准差，即

(13)

(14)

可靠性指标βuv1，βuv2定义为

(15)

(16)

3 串联系统可靠性敏感度分析

考虑到电梯系统具有多阶固有频率、多个激振频率的特点，当激振频率落在某阶固有频率的共振区间时，会使整个系统发生共振。因此，含有多频激励的系统频率可靠性模型为串联系统。依据串联系统的可靠性分析理论[9]，得到系统的失效概率。

(17)

(18)

其中：R为串联系统的可靠度。

通过对系统失效状态进行敏感度分析，得到影响系统失效的敏感因子。通过修改系统的设计参数来改变系统的固有频率，使其远离激振频率以避开共振区。根据可靠性敏感度的定义，可靠度R对设计参数bs的均值敏感度和方差敏感度分别为

(21)

(22)

其中：σs，Var(bs)分别为基本随机变量bs的标准差和方差；R*为系统的可靠度。

4 共振问题的可靠性鲁棒设计

鲁棒设计是指允许产品的设计变量和控制容差在一定范围内波动，仍能保证产品具有较高的可靠度和稳定性，即能够抵抗一定程度非预期随机因素的干扰。因此在优化设计的基础上，结合系统结构的可靠度要求，以可靠性指标作为约束条件，将随机变量的敏感度融合到目标函数中，将可靠性鲁棒设计归结为求解多目标函数的优化设计问题。当随机动态结构系统受到某一激振力时，激振力的频率不同，强迫振动的振幅也随之不同。为了满足系统的稳健要求，即要求随机系统的固有频率远离系统的激振频率，避开共振区，从而保证系统安全可靠运行。随机系统的频率可靠性鲁棒设计模型表示为

5 实例分析

5.1 模态

以某样梯为研究对象，额定载重为1 150 kg，轿厢速度为1.7 m/s，提升高度为42 m。曳引机转速为492 r/min，反绳轮的转速为223 r/min，激振频率分别为f1=7.96 Hz，f2=3.625 Hz。其他主要部件结构参数如表1所示。

现有的合规管理制度仅对商务行为的合规管理，即“狭义”合规管理进行了约束，对非商务行为的合规管理，即“广义”合规管理没有明确的要求；对合规风险评估、合规审查、合规评价等管理内容也没有细化；对重要风险领域，如“礼品和款待”“商业伙伴合作”也没有具体的行为准则。同时企业规章制度执行不到位，未能做到有制度必依。真正落实的时候却大打折扣，从而有章不循、不按制度办事、违章操作、违反规定等现象时有发生，使得有的规章制度成了摆设。

表1 电梯系统动力参数

根据式(1)～(9)对电梯系统纵向振动进行模态分析，得到系统各阶频率与轿厢位移x4变化曲线，如图2所示。可以看出，系统频率ω1在3.195～3.295之间，可见ω1与轿厢位移x4关系不大，2阶频率在9.31～11.68之间变化，其他高阶频率与轿厢位置较为敏感。由激振频率与系统固有频率的关系可知，激振频率f1与ω2共振区接近，易发生共振。激振频率f2落在系统1阶固有频率的共振区内，代入式(9)～(11)，λ取0.15，系统失效概率Pf=1，即系统发生共振。

图2 系统各阶固有频率变化曲线Fig.2 Variable cures of system natural frequencies

5.2 试验结果

如图3所示，利用电梯乘运质量检测工具PMT对轿厢振动进行测试。发现轿厢的纵向振动比较强烈，最大峰峰值为17.1mg。选择恒速阶段进行频谱分析，如图4所示。可见，轿厢振动主要是在3.625 Hz引起的，该频谱与轿厢反绳轮转动频率相对应。结合系统模态分析可知，轿厢反绳轮激振频率与系统一阶频率发生共振，表明理论分析与试验结果吻合，证明所建振动模型是合理的。

图3 轿厢振动时间历程Fig.3 Time domain plot of car vibration

图4 轿厢纵向振动幅频曲线Fig.4 Amplitude frequency curve of longitudinal vibration

5.3 敏感度

根据电梯系统的敏感度分析可以得出系统设计变量与系统固有频率的敏感顺序。本系统选取参数k1，k2，k3和k4作为系统的随机变量，刚度变量的分布情况在均值上下±10%范围内变化，且服从正态分布。求解振动微分方程只能得到随机变量与系统频率响应的数值解，不能得到b={k1,k2,k3,k4}T与固有频率f1的显性函数表达式。因此，笔者采用优化软件Isight进行试验设计，通过集成Matlab编制的程序进行超立方拉丁试验分析。将随机变量b={k1,k2,k3,k4}T抽样81次，作为BP神经网络训练的样本，将每次分析的结果作为BP神经网络的响应值。通过神经网络训练，拟合得到随机变量与ω2之间的显性函数关系式。由图5可知，经过119次训练，神经网络模型精度可达到10-6。

图5 BP神经网络训练误差Fig.5 BP neural network training error

如图6所示，为了确保神经网络拟合函数的准确性，对随机参数按照正交试验方法抽样16次进行验证，并与Matlab编制的振动微分方程求得的理论值进行比较，证明了神经网络模型的可靠性。

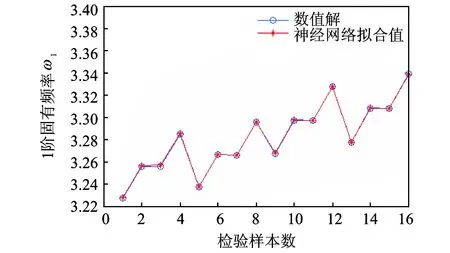
图6 均值处随机样本模拟检验图Fig.6 Random sampling simulation test in mean

将神经网络拟合后的函数代入式(9)～(17)，得到系统的准失效概率Pf=1，由此可知该系统已发生共振失效。代入式(18)～(21)对其进行敏感度分析，得到可靠度对随机变量均值和方差的敏感度为

5.4 稳健设计

为了达到减少共振发生的风险和系统设计变量在误差范围内变化对系统共振不敏感、满足系统稳健的要求，通过修改设计变量来改变系统共振区间，以达到远离激振频率。式(20)取3个目标函数

建立约束条件

优化后各随机变量的均值为k1*=490 080, k2*=9 986 000, k3*=819 900, k4*=2 804 200。将优化后的随机参数代入式(9)～(21)，系统可靠度为R*=0.999 964 89,均值、方差的敏感度为

通过优化前后可以看出系统具有较高的可靠度，随机变量的敏感度也大大降低，满足稳健设计的要求。

5.5 稳健设计后试验结果

从图7可知，轿厢的纵向振动明显减低，最大峰峰值由17.1 mg降低到6.9 mg。如图8所示，对恒速阶段进行频谱分析，3.625 Hz频率的幅值由1.836 mg降低到0.424 1 mg。其他频率的振动也大大降低，从而使系统振动满足要求。

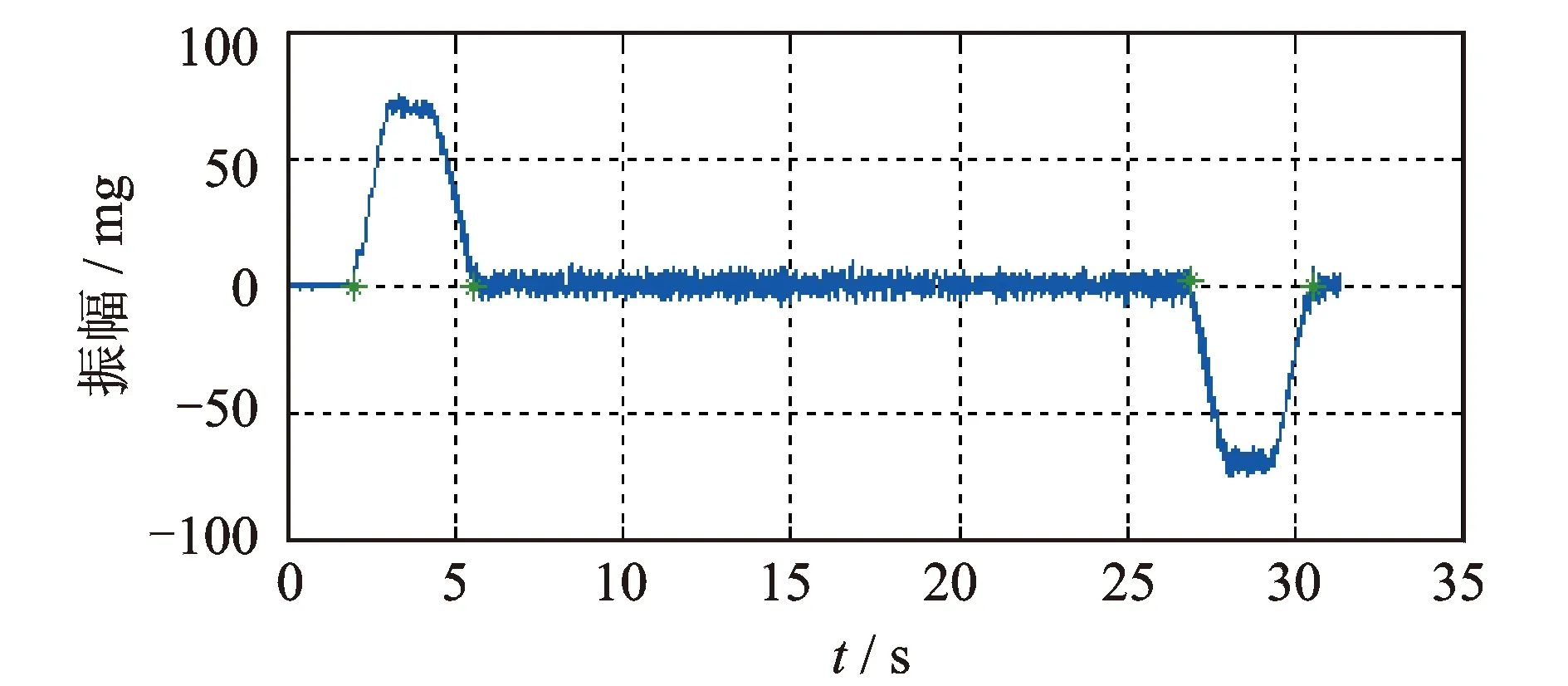
图7 轿厢垂直振动时间历程Fig.7 Time domain plot of car vibration in vertical direction

图8 稳健设计后的轿厢纵向振动幅频曲线Fig.8 Amplitude frequency curve of longitudinal vibration by robust design

6 结论

1) 考虑电梯曳引绳在运动过程中的变刚度特性，对电梯系统建立了7自由度振动微分方程，得到系统各阶固有频率与轿厢位移的变化曲线。结果显示，低阶固有频率与轿厢位置变化影响不大，高阶频率与轿厢位置变化敏感。

2) 对电梯系统动力学模型进行模态分析，指出曳引机的激振频率与系统固有频率较近，容易发生共振。结合系统实际振动测试，得到系统垂直振动超标，表明系统激振频率与固有频率较近发生共振。

3) 在频率可靠性敏感度分析的基础上，对系统进行可靠性稳健设计。结果表明，通过修改设计变量可以使系统达到可靠度的要求，同时满足稳健设计的要求。

4) 对振动微分方程进行数值分析，利用集成优化工具Isight对系统结构随机变量和响应进行试验设计。借助人工神经网络拟合函数的优势，得到随机变量与系统响应的解析方程。结合可靠性敏感度技术与稳健设计理论，对随机结构系统进行敏感度分析和稳健设计。该方法具有较高的计算效率和求解精度，可以作为随机结构可靠性灵敏度分析和稳健设计的一种有效方法。

[1] Lorsbach G P. Analysis of elevator ride quality, vibration[J]. Elevator World, 2003, 51(6): 108.

[2] 王向红, 朱昌明, 杨广全, 等. 电梯系统机电耦合模型仿真研究[J]. 系统仿真学报, 2007, 19(10): 2328-2331.

Wang Xianghong, Zhu Changming, Yang Guangquan, et al. Simulation for electromechanical coupling model of elevator systems[J]. Journal of System Simulation, 2007, 19(10): 2328-2331.(in Chinese)

[3] Nai K, Forsythe W. Improving ride quality in high-speed elevators[J]. Elevator World, 1997(6): 88-93.

[4] Kang J K, Sul S K. Vertical-vibration control of elevator using estimated car acceleration feedback compensation[J]. IEEE Transactions on Industrial Electronics, 2000, 47(1): 91-99.

[5] 胡振东，赵珊珊.高速电梯系统时变动力学模型与分析[J].力学季刊,2002, 23(3): 422-426.

Hu Zhendong, Zhao Shanshan. Modeling and analysis of time-varying dynamics for high-speed elevator[J]. Chinese Quarterly of Mechanics, 2002, 23(3): 422-426.(in Chinese)

[6] 包继虎，张鹏，朱昌明.变长度提升系统钢丝绳纵向振动特性[J].振动与冲击,2013, 32(15): 173-177.

Bao Jihu, Zhang Peng, Zhu Changming. Longitudinal vibration of rope hoisting systems with time-varying length[J]. Journal of Vibration and Shock, 2013, 32 (15): 173-177. (in Chinese)

[7] 张聚, 李平. 参数不确定电梯机械系统振动的 H∞鲁棒控制[J]. 振动与冲击, 2001, 20(4): 22-24.

Zhang Ju, Li Ping. Active vibration H∞infinity robust control for the mechanical system of elevator with parameter uncertainty[J]. Journal of Vibration and Shock, 2001, 20(4): 22-24. (in Chinese)

[8] Zhang Y, Lü C, Zhou N, et al. Frequency reliability sensitivity for dynamic structural systems[J]. Mechanics Based Design of Structures and Machines, 2010, 38(1): 74-85.[9] Melchers R E, Ahammed M. A fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability[J]. Computers & Structures, 2004, 82(1):55-61.

[10]吕春梅，张义民，李鹤，等. 随机连续杆纵向振动系统频率可靠性稳健分析[J]. 振动、测试与诊断, 2013, 33(5): 794-798.

Lü Chunmei, Zhang Yimin, Li He, et al. Frequency reliability robust of random axial vibration of rod system with arbitrary distribution[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(5): 794-798.(in Chinese)

[11]Wu Y T. Computational methods for efficient structure reliability and reliability sensitivity analysis[J]. AIAA Journal, 1994, 32(8): 1717-1723.