梁结构碰撞位置的定量诊断方法

2016-12-07姚红良闻邦椿

振动、测试与诊断 2016年4期

关键词：谐波定量故障诊断

姚红良，孙云，许琦，闻邦椿

(东北大学机械工程与自动化学院沈阳，110819)

梁结构碰撞位置的定量诊断方法

姚红良，孙云，许琦，闻邦椿

(东北大学机械工程与自动化学院沈阳，110819)

针对机械设备中广泛存在的各种梁结构常因振动等原因与外界发生碰撞而不能及时准确检测出碰撞位置的问题，提出了一种梁结构碰撞故障位置的定量诊断方法。基于谐波平衡理论推导出碰撞梁响应信号中高次谐波成分之间的对比关系，根据无故障系统和故障系统信号的响应之差，提取某一高阶谐波分量，结合梁结构系统的有限元模型来诊断碰撞故障的具体位置。对悬臂梁和复杂梁结构的数值仿真和实验结果显示，该诊断方法能够准确判断梁结构的碰撞故障位置。通过改变未知参数的实验表明，该方法具有较好的稳健性，不需要大量的先验数据，仅用两个测点的响应数据就可以诊断出故障的准确位置，简单又便于实现在线诊断。

碰撞；定量诊断；谐波分量；梁结构

引言

梁类结构广泛存在于各类机械装备中，其在设备运行中可能会发生各种故障。复杂梁类结构体积巨大，往往因碰撞而发生严重破坏，从而影响设备的安全运行。因此，梁类结构碰撞故障的诊断研究具有重要意义。

目前，梁类结构的故障诊断方法可以分为定性诊断方法和定量诊断方法两大类。定性诊断方法多是通过对采集到的振动信号进行分析处理来判断故障的存在。Nguyen等[1]应用自适应神经结构和小波分析的方法识别梁结构故障。Chen等[2]利用神经网络方法对梁结构表皮剥落损伤和连接松动问题进行诊断，该方法对微小故障具有很好的敏感性。罗跃纲等[3]利用小波分析和神经网络相结合的方法诊断设备故障。Du等[4]使用神经网络和PSOSAEN算法对梁结构进行故障诊断，该方法具有良好的容错性。定性诊断方法能够直接迅速地判断结构是否存在故障，但不能直接确定故障的位置等定量参数。定量诊断方法需要根据系统本身的物理特性进行建模，将振动信号与模型结合进行故障诊断，从而诊断出故障的具体位置和严重程度。文献[5]结合扩展卡尔曼估计算法及递推最小二乘估计算法进行梁结构的损伤诊断。文献[6]提出采用适宜求解奇异性问题的小波有限元法检测梁类结构多裂纹参数。文献[7]提出一种提升小波包分解、多传感器特征融合和神经网络模式分类相结合的结构损伤诊断方法，对复合材料机翼盒段进行损伤特征辨识。国外对梁类结构故障的定量诊断方法也很多。Sinou等[8]提出利用裂纹梁结构的非线性振动响应和高阶频响函数检测故障位置。文献[9]利用小波变换方法检测梁裂纹位置。文献[10]提出利用非线性输出频率响应函数来诊断梁的裂纹故障。文献[11]提出了首先利用模态变化诊断裂纹位置，然后通过响应敏感度来诊断裂纹大小的二步方法。定量诊断方法还可与许多方法结合，使数学计算更加容易，如结合奇偶校验法[12]、基于沃尔泰拉模型[13]等。由于定量诊断方法既可以定量诊断出故障的位置，也可以诊断出故障的严重程度，对机械设备的预知维修有很大的贡献。以上方法大多应用于梁类结构的裂纹类故障，而目前针对梁类结构碰撞故障的诊断方法很少。

鉴于梁类结构碰撞故障诊断的重要性，笔者提出一种定量的梁结构碰撞故障位置诊断方法。该方法通过建立梁结构的动力学模型，利用故障振动响应的高次谐波成分进行故障诊断。采用数值仿真和实验验证的方法分别对简单梁结构和复杂梁结构进行研究，验证了该诊断方法的正确性和有效性。

1 梁结构的动力学模型

梁结构模型采用欧拉梁单元组成，每个单元有两个节点，每个节点包含6个自由度，分别为x，y，z方向的平动和绕x，y，z方向的转动，单元模型如图1所示。

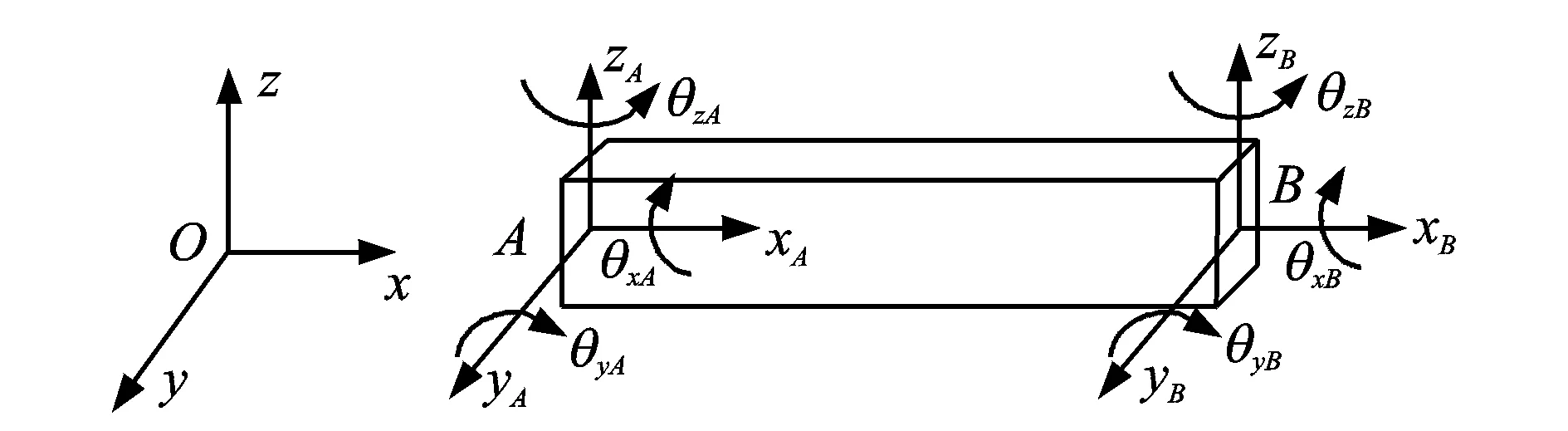
图1 梁单元有限元模型Fig.1 Finite element model of beam element

梁结构的动力学方程为

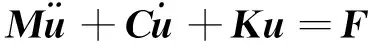
(1)

其中：M，C，K分别为质量、阻尼、刚度矩阵(设系统有N个节点，则矩阵均为6N×6N阶方阵)；u为振动响应矢量；F为偏心电机产生的激励矢量。

设系统碰撞故障发生在节点L处，则故障系统的动力学方程为

(2)

其中：T6L-3为碰撞位置矢量；Pz为碰撞力在节点L处z方向上的分量；ur为故障的振动响应矢量。

式(2)-式(1)，得

(3)

其中：Δu=ur-u。

式(3)即为故障系统剩余振动量动力学方程。由式(3)可以看出，碰撞力可以被视为系统的外加等效力，系统本身的质量、阻尼和刚度矩阵保持不变。

2 定量诊断方法推导

将广义故障力也展开成各阶谐波分量和的形式，即

(5)

其中：Aieijωt为碰撞故障力的第i阶谐波分量。

根据谐波平衡理论，有

(6)

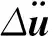
(7)

利用式(7)即可诊断系统的碰撞故障位置。设梁结构系统的两个任意节点号为n1和n2，由式(7)得到

(8)

当δL取最小值时，L即为故障节点位置。取系统响应中的前N阶谐波分量，则故障系统的碰撞故障力为

(9)

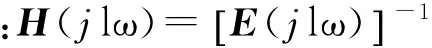
3 诊断步骤

本研究方法的具体诊断步骤如下：

2) 计算系统的频率-加速度响应函数矩阵E(jlω)；

3) 建立下式并计算δL

(10)

4) 当δL取最小值时，L即为系统的碰撞位置。

4 数值模拟及实验

4.1 悬臂梁结构仿真结果

采用欧拉梁单元模型建立梁结构的有限元模型，如图2所示。悬臂梁长为400 mm，宽度为40 mm，厚度为3.4 mm，截面为矩形。将其划分为11个单元，每个单元长度为40 mm，共11个节点，每个节点包含6个自由度。弹性模量为210 GPa，泊松比为0.3，材料密度为7 850 kg/m3。一端全约束(节点1)，电机所在位置(节点11)采用mass21集中质量单元。

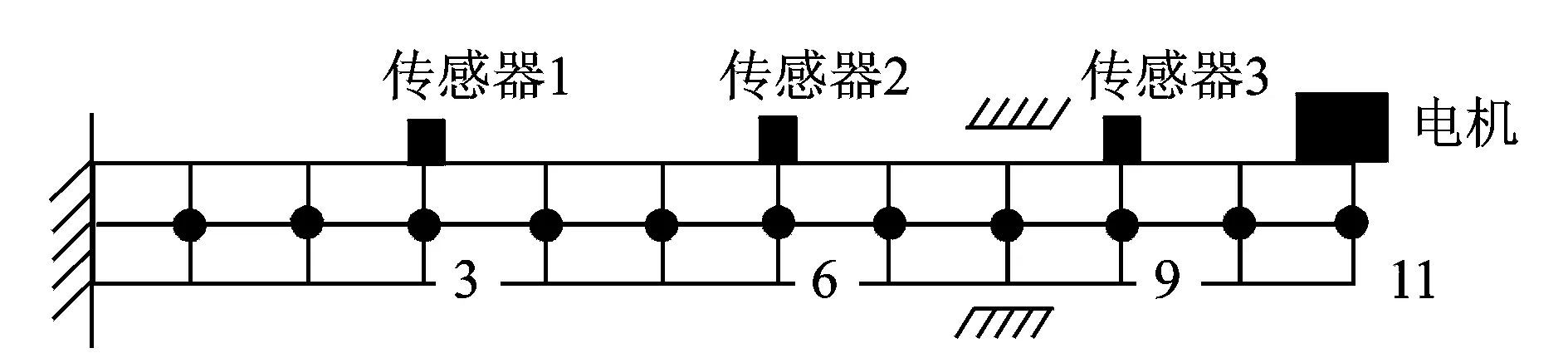
图2 悬臂梁结构有限元模型Fig.2 Finite element model of cantilever structure

激振力加载在节点11处，方向垂直于梁表面，大小为1.132 N，频率为146 Hz；碰撞力加载于节点8，方向垂直于梁表面。节点8的响应如图3所示，频域响应中出现了丰富的高倍频成分。取节点6，8和节点8，9两组观测点，采用2X数据进行诊断，诊断结果如图4所示。两组数据诊断的最小值均在节点8处，即可准确判断出碰撞故障位置。

图3 节点8的响应Fig.3 Response at node 8

图4 悬臂梁仿真诊断结果Fig.4 Diagnosis results of cantilever beam by simulation signals

4.2 复杂梁结构仿真结果

假设某复杂梁结构(框架结构)高为450 mm，分为3层，每层柱高为150 mm，x方向上的梁长为250 mm，z方向上的梁长为150 mm。梁和柱为等直径的圆柱体，圆柱体的截面半径为10 mm，有限元模型如图5所示。框架结构最下端4个节点全约束，材料密度为7 850 kg/m3，弹性模量为210 GPa，泊松比为0.3。

图5 复杂梁结构有限元模型Fig.5 FEM of the complex beam structure

对节点11施加x方向的正弦激振力，激振力幅值为1 N，激振频率为125 Hz，设碰撞接触刚度为1×108N/m，碰撞间隙为1×10-3m。

假设碰撞故障发生在节点6，取节点8和节点10，节点8和节点12两组观测点。诊断结果如图6所示，结果验证了该方法在复杂梁类结构诊断中的有效性。

图6 复杂梁结构仿真诊断结果Fig.6 Diagnosis results of complex beam structure by simulation signals

4.3 实验结果

实验装置如图7所示。结构与悬臂梁仿真模型相同，激振频率为148 Hz，碰撞方向垂直于悬臂梁表面,传感器布置在节点3，6和节点9。使用B&K Pulse信号采集器以及配套的加速度传感器对振动信号进行采集。

图7 悬臂梁实验装置Fig.7 Experimental equipment

正常情况和碰撞情况下节点6的时域响应和频谱图结果分别如图8，9所示。从图9可以明显地看出响应呈非线性特征。

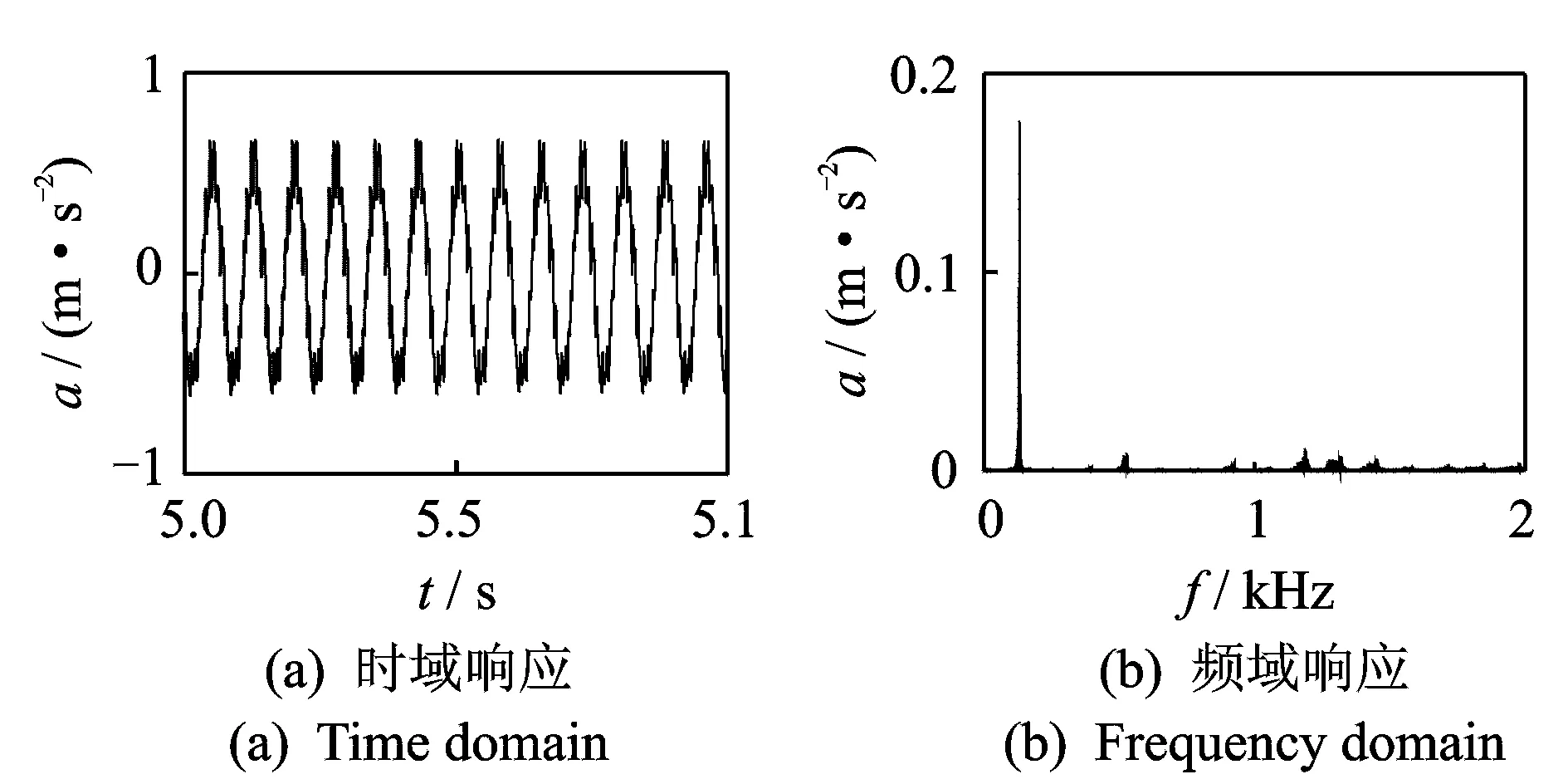
图8 非碰撞时节点6的响应曲线Fig.8 Response at node 6 without impact

图9 碰撞时节点6的响应曲线Fig.9 Response at node 6 with impact

使用相同节点的响应信息，但是取不同阶谐波分量，分别采用传感器3，9响应剩余量的2X谐波分量和传感器6，9响应剩余量的4X谐波分量作为诊断依据，诊断结果如图10所示。可见，两种情况都能准确地诊断出碰撞故障位置，验证了诊断方法的正确性和可行性。

图10 实验诊断结果Fig.10 Experiment diagnosis results

4.4 方法稳健性分析

由于本研究方法采用了结构动力学模型，因此必须分析动力学模型的精度对诊断结果的影响，即模型不精确时本研究方法的稳健性。由于动力学模型中质量和刚度都容易确定，而阻尼的确定比较困难，因此改变阻尼的大小，观测其对诊断结果的影响。在建模时设计的材料阻尼基础上，将阻尼矩阵C分别乘以0.01，0.1，10和100，得到的诊断结果如图11所示。当系统阻尼整体改变很多时，诊断结果与原结果基本无差别，验证了本研究方法的稳健性。

图11 改变阻尼诊断结果Fig.11 Experiment results when damping changed

5 结论

1) 结合谐波平衡理论，推导出存在碰撞故障时梁结构的振动响应和碰撞位置之间的关系，提出梁结构碰撞位置的定量诊断方法，并给出了诊断的具体步骤。

2) 进行故障诊断时，仅需任意两点的振动响应数据就可以定量诊断出故障位置，方法简单有效，便于实现在线诊断。

3) 仿真和实验结果表明，该方法具有很好的效果。改变阻尼的实验表明该方法具有较强的稳健性。

[1] Nguyen S D, Ngo K N, Tran Q T, et al. A new method for beam-damage-diagnosis using adaptive fuzzy neural structure and wavelet analysis[J]. Mechanical Systems and Signal Processing, 2013, 39(1-2): 181-194.

[2] Chen Qian, Chan Y W, Worden K. Structural fault diagnosis and isolation using neural networks based on response-only data[J]. Computers and Structurese, 2003, 81(22-23): 2165-2172.

[3] 罗跃纲, 陈长征, 曾海泉, 等. 基于信息融合的集成小波神经网络故障诊断[J]. 东北大学学报: 自然科学版, 2002, 23(8): 802-805.

Luo Yuegang, Chen Changzheng, Zeng Haiquan, et al. Integrated wavelet neural networks in fault diagnosis based on information fusion[J]. Journal of Northeastern University: Natural Science Edition, 2002, 23(8): 802-805. (in Chinese)

[4] Du Shichang, Xi Lifeng. Fault diagnosis in assembly processes based on engineering-driven rules and PSOSAEN algorithm[J]. Computers & Industrial Engineering, 2010, 60(1): 77-88.

[5] 雷鹰, 江永强. 输入输出信息有限观测下的结构损伤诊断[J]. 振动、测试与诊断, 2012, 32(5): 736-740.

Lei Ying, Jiang Yongqiang. Structural damage detection technique with limited input and output measurement signals[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5): 736-740. (in Chinese)

[6] 陈雪峰, 李兵, 訾艳阳, 等. 梁类结构多裂纹微弱损伤的小波有限元定量检测方法[J]. 机械工程学报, 2005, 41(7): 126-130.

Chen Xuefeng, Li Bing, Zi Yanyang, et al. Multiple infant cracks detection for beam-type structures by wavelet finite element method[J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 126-130. (in Chinese)

[7] 陈换过, 江金寿, 李剑敏, 等. 基于提升小波包和神经网络的结构损伤检测[J]. 振动、测试与诊断, 2013, 33(1): 116-121.

Chen Huanguo, Jiang Jinshou, Li Jianmin, et al. Damage detection of wing-box based on lifting wavelet packet transform and neural network[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(1): 116-121. (in Chinese)

[8] Sinou J J. On the use of non-linear vibrations and the anti-resonances of higher-order frequency response functions for crack detection in pipeline beam[J]. Mechanics Research Communications, 2012, 43: 87-95.

[9] Wu Nan, Wang Quan. Experimental studies on damage detection of beam structures with wavelet transform[J]. International Journal of Engineering Science, 2011, 49(3): 253-261.

[10]Peng Zhike, Lang Ziqiang, Billings S A. Crack detection using nonlinear output frequency response functions[J]. Journal of Sound and Vibration, 2007, 301(3): 777-788.

[11]Lu X B, Liu Jike, Lu Zhongrong. A two-step approach for crack identification in beam[J]. Journal of Sound and Vibration, 2013, 332(2): 282-293.

[12]Beckerle P, Schaede H, Butzek N, et al. Balancing filters: an approach to improve model-based fault diagnosis based on parity equations[J]. Mechanical Systems and Signal Processing, 2012, 29: 137-147.

[13]Tang Hao, Liao Yuhe, Cao Junyi, et al. Fault diagnosis approach based on volterra models[J]. Mechanical Systems and Signal Processing, 2010, 24(4): 1099-1113.