回归模型与VEC模型在旅游业的应用研究

李 杰，刘兆鹏，费时龙，任 敏

（ 宿州学院 数学与统计学院，安徽 宿州 234000 ）

回归模型与VEC模型在旅游业的应用研究

李 杰，刘兆鹏，费时龙，任 敏

（ 宿州学院 数学与统计学院，安徽 宿州 234000 ）

根据多元线性回归模型理论，摘取安徽省近些年旅游业相关原始数据进行相关性分析，给出了多重因素下的线性回归模型，并对模型进行优化，修复了严重共线性。进一步，运用VEC模型预测安徽省旅游业的发展前景，为安徽省的旅游发展和规划提供参考。

旅游业； 回归模型； VEC模型； 检验

1.旅游需求计量分析模型的各因素

根据安徽省统计年鉴获取的历年有关数据[1]，进行简单的图表处理得图1、图2、表1、表2和表3。

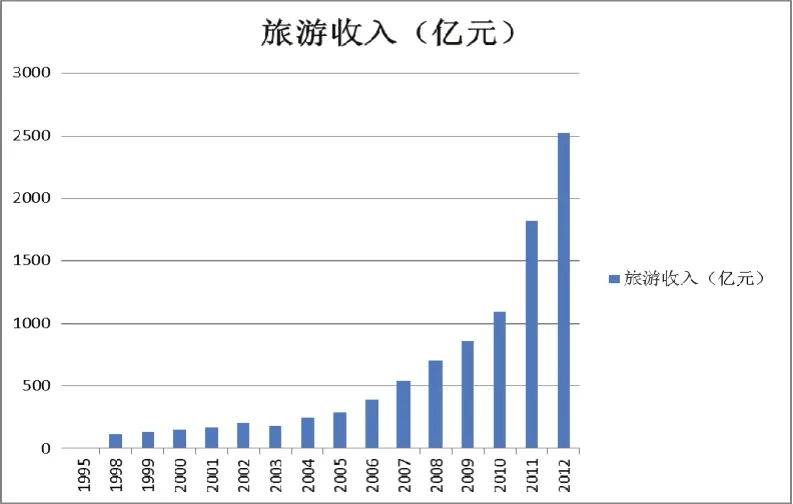
图1 历年安徽省旅游收入

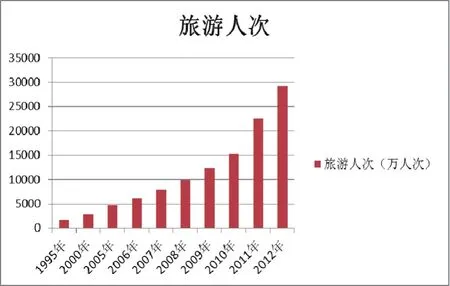
图2 历年安徽省旅游人次

2.模型的设定及其检验

2.1.相关性分析及模型建立

根据影响因素设五个相关变量[2]。X2：来皖旅游人数；X3：来皖游客人均花费；X4：旅游者可支配收入；X5：公路里程；X6：铁路里程。Y表示安徽省省内旅游需求，对Y进行初步回归分析。为此设定了如下形式的计量经济模型[3]：

其中tY为第t年安徽省省内旅游需求。

为估计模型参数，本文选用安徽省统计年鉴上1999年至2012年的统计数据。利用EViews软件，生成Yt、X2、X3、X4、X5、X6等数据，采用这些数据对模型进行OLS回归，由OLS回归结果可知该模型可决系数很高，F检验值575.5910，明显显著。但是当α=0.05时，的系数t检验不显著，而且X6系数的符号是负号，与实际情况不符，这表明很可能存在严重的多重共线性[4]。

计算解释变量的相关系数，选择X2、X3、X4、 X5、X6的数据，点“view/correlation”得相关系数

矩阵，如表4所示。由表4可以看出，各解释变量间的相关系数较高，这表明存在严重共线性。

2.2.修正多重共线性

依次作Y对X2、X3、X4、X5、X6的一元回归，其中加入X的方程最大。以X为基础，顺次加入其他变量逐步回归，经比较，新加入的X3的方程=0.9912,改进最大，而且各参数的t检验显著，选择保留X3，再加入其他新变量逐步回归。在X、X基础上加入X后的方程有所改善，且各参数的t检验都显著。保留X4，再加入其他新变量逐步回归。当加入X时，有所增加，但其参数的t检验不显著。加入X后，也有所增加，但其参数的t检验不显著，且参数为负值，不合理。从相关系数也可以看出，X5、X6与其他变量高度相关，这说明主要是X5、X6引起了多重共线性，予以剔除。

表1 全国城乡居民人民币储蓄情况（1999年～2012年）（单位：亿元）

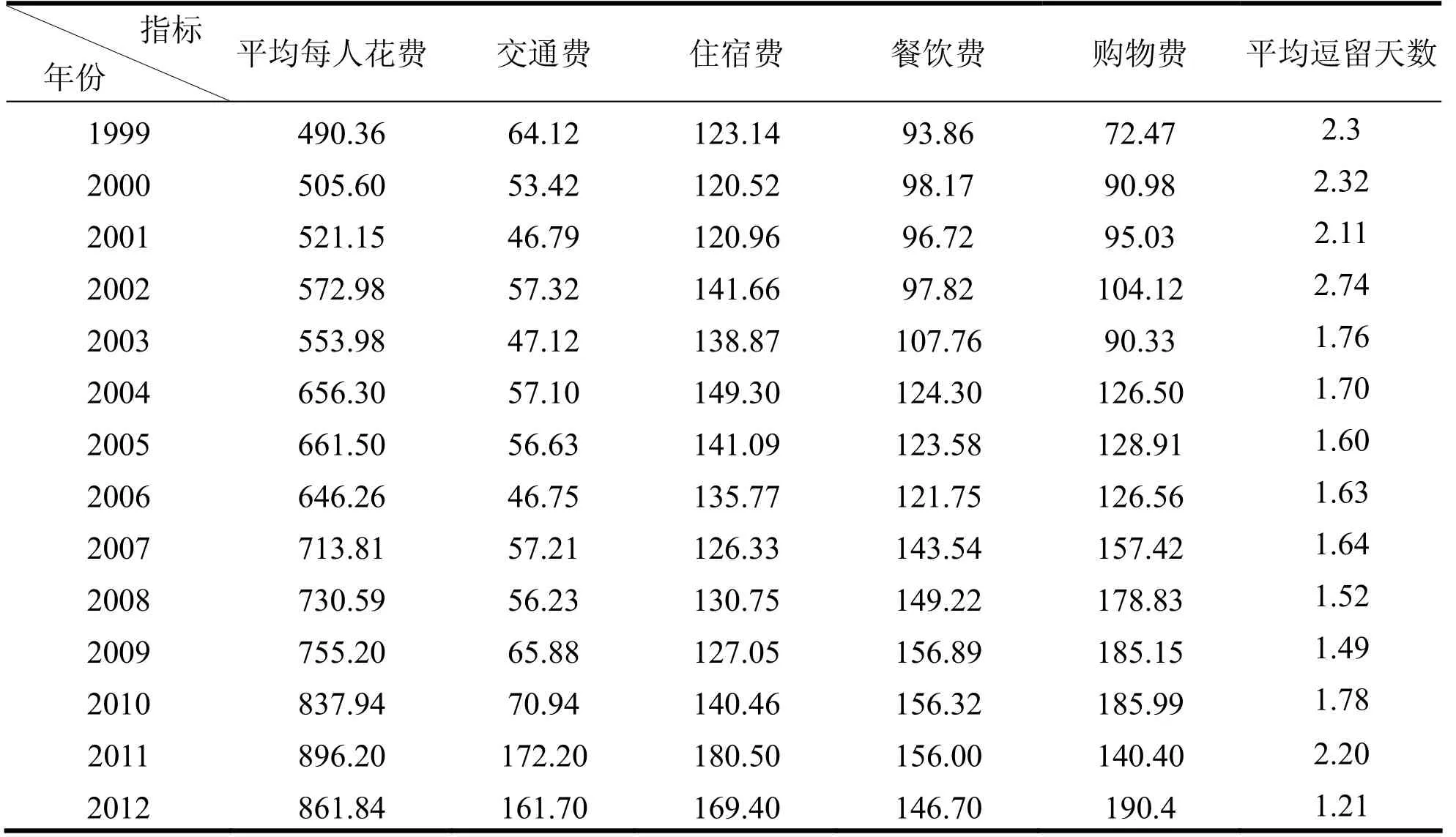
表2 历年来皖游客在安徽省的消费（单位：元）

表3 安徽省公路、铁路的运营里程

2.3.优化模型

修正后的回归模型为：

逐步回归后的结果虽然实现了减轻多重共线性的目的，但反映基础设施类影响的因素X5、X6也一并从模型中剔除了，可能会带来设定误偏。

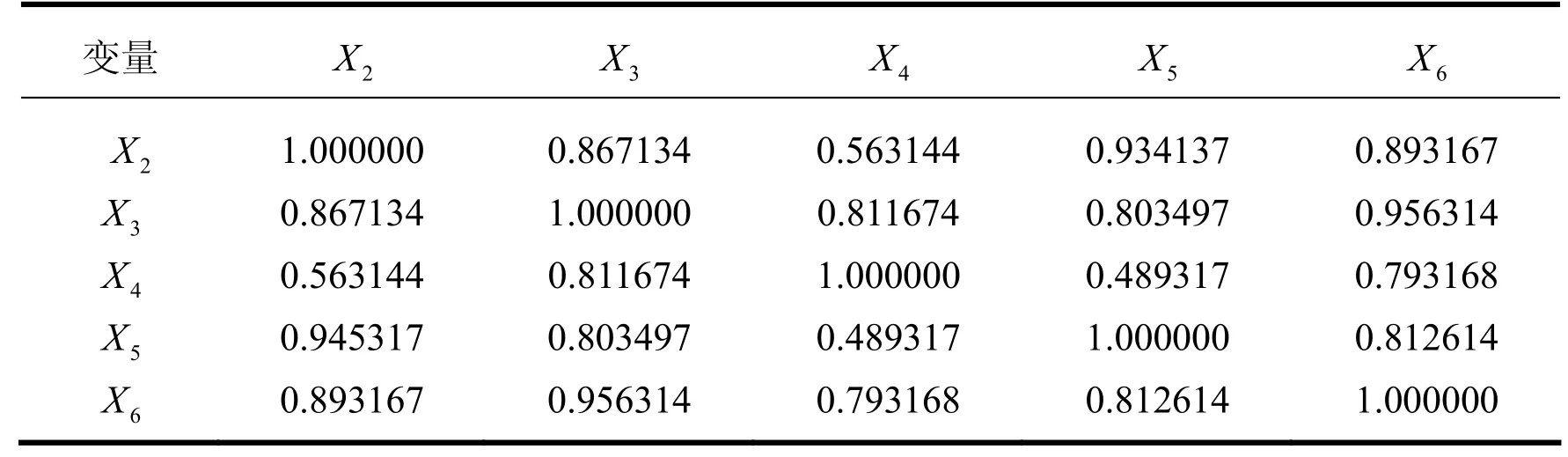
表4 相关系数矩阵

3.对安徽省旅游需求进行回归预测

3.1.单位根检验

使用PP检验，根据序列的形态，对各列采用同时包含截距和趋势项的检验，最大滞后期采用Eview5.0[5]。根据样本量自动推荐的q值序列，LY, LX2,LX3,LX4,LX5,LX6的PP值分别为-2.30、-2.02、-0.59、-0.09、-1.82、-1.39，对应95%置信水准的临界值是-3.57，故均不能拒绝时间序列存在单位根的假设，从而它们都是非平稳的。对经过一阶差分后序列进行单位根检验，所得PP统计量分别为-4.74、-3.82、-4.27、-4.37、-3.62、-5.65，至少可以在95%的置信水准下拒绝原假设。从每个变数的序列图和一阶差分图中可以看出，每个对数化变数的序列图有明显的趋势，是非平稳序列，而每个对数化变数的差分序列图基本上在0附近波动，近似于平稳序列。以上分析表明，6个对数化的产生序列都是I（1）序列，满足协整检验的条件。

3.2. 协整检验

表5是年度资料在滞后区间为（1,1）时的JJ检验结果。从表5可以看出，有4个拟然比统计量大于99%水准下的临界值，因而有4个原假设被拒绝，即存在多个协整关系。本文只关心拟然比统计量=329.5468时的协整假定关系下经过标准化的协整系数[6]，如表6所示。

表5 Johansen协整检验结果

表6 标准化协整系数表

将上述协整关系用数学运算式表达出来，使其结果等于vecm，具体如下：

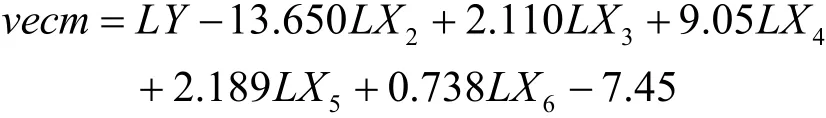
对序列vecm进行单位根检验，得出其是平稳序列，并且其取值在0附近波动，验证了协整关系的正确性。上式反应了6个时间序列之间长期稳定的平衡关系。

3.3.向量误差修正模型（VEC）

表6表明6个序列是协整的，并且通过验证的只有一个协整关系[7]，可以建立该6个变量的VEC模型。根据Eview软件的运行可以得到VEC模型的参数估计值，估计结果如下：

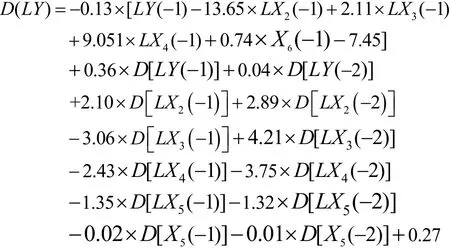
研究年度VEC模型[8]整体效果的主要标准是AIC和SC，模型的AIC=-14.90264，SC=-11.03475都较小，说明该模型的整体模拟效果较好。

保留样本模型误差验证：（1）RMSE=1960.17；（2）MAE=4139；（3）MAPE=10.55%；（4）Theil’s IC=0.017。对2016年至2019年的安徽省游客量进行预测，预测资料见表7：

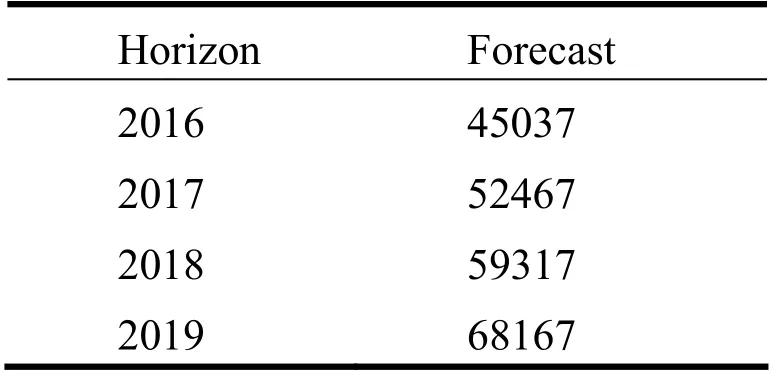
表7 安徽省游客量预测值（年度）

4.结论

第一个多元线性回归模型研究了安徽省旅游需求的影响因素，因为公路里程和铁路里程引起了严重的多重共线性，所以被剔除。由模型可以看出，国内旅游人数和可支配收入对旅游需求有很大影响,因此，如何最大程度的吸引游客和控制旅游物价应该是安徽省旅游机构的当务之急。

第二个分析运用了VEC模型，得出了安徽省游客量的未来预测，为安徽省的旅游发展和规划提供了很好的参考。如完善公共服务体系：扩大安徽省

内旅游公路的覆盖率；注重旅游形态方面的协调发展转变：随着当今生活水平的不断提高，人们越来越倾向于自驾游和自助游，传统的旅游模式已经不能满足当前的市场需求，旅游业应顺应这种发展趋势；结合省内的资源和区位优势，不断创新，多层次多角度丰富旅游产品：全面发展休闲观光度假游。

[1] 安徽省统计局.2012安徽统计年鉴[M].北京：中国统计出版社，2012.

[2] 庞皓，李南成.计量经济学学[M].四川：西南财经大学出版社，2002.

[3] 何晓群，刘文卿.应用回归分析[M].北京：中国人民大学出版社，2001.

[4] 王燕.应用时间序列分析，第三版[M].北京：中国人民大学出版社，2011.

[5] 姜启源.数学模型[M].北京：高等教育出版社，1993.

[6] 沈继红，施久玉，高搬滨，等.数学建模[M].哈尔滨：哈尔滨工程大学出版社，1998.

[7] 余建英，何旭宏.数据统计分析与SPSS应用[M].北京：人民邮电出版社，2003.

[8] 李柏文.国内外城镇旅游研究综述[J].旅游学刊，2010，（6）：28-35.

The application of regression model and VEC model in tourism research

LI Jie, Liu Zhaopeng, Fei Shilong, Ren Min ( Department of mathematics and statistics, Suzhou University, Suzhou, Anhui 234000, China )

According to the theory of multiple linear regression model, gather tourism related original data in Anhui province in recent years, for correlation analysis. Multiple linear regression model in the case of factors are given, and optimize the model, repair the serious collinearity. Further, use the VEC model to predict the prospects for development of tourism in Anhui province, provide reference for Anhui province's tourism development and planning.

the tourism industry, the regression model, the VEC model, test

O212

A

1673-9639 (2016) 04-0173-05

（责任编辑 毛 志）（责任校对 印有家）

2015-04-13

高校创新训练项目“Mean-CvaR模型及其两基金定理的应用研究”（AH201410379077）；高校自然科学研究项目（KJ2016A770）；宿州学院教学研究项目（szxy2015jy09；szxyjyxm201322）。

李 杰（1983-），男，安徽六安人，硕士，研究方向：概率论与数量统计。