基于自适应权值的点云三维物体重建算法研究

林　晓， 王燕玲， 朱恒亮， 胡甘乐， 马利庄， 李鲁群

(1. 上海师范大学信息与机电工程学院，上海 200234；2. 洛阳师范学院信息技术学院，河南 洛阳 471022；3. 上海交通大学电子信息与电气工程学院，上海 200240)

基于自适应权值的点云三维物体重建算法研究

林晓1, 2， 王燕玲2， 朱恒亮3， 胡甘乐3， 马利庄3， 李鲁群1

(1. 上海师范大学信息与机电工程学院，上海 200234；2. 洛阳师范学院信息技术学院，河南 洛阳 471022；3. 上海交通大学电子信息与电气工程学院，上海 200240)

基于三维扫描点云数据的三维物体重建是计算机图形学中非常重要的课题，在计算机动画、医学图像处理等多方面都有应用。其中基于最小二乘问题的 Levenberg-Marquart算法和基于极大似然估计的 M-Estimator算法都是不错的方案。但是当点的数量过多过少或者点云中有噪声时，这些方案产生的结果都会有较大的误差，影响重建的效果。为了解决这两个问题，结合 Levenberg-Marquart算法和 M-Estimator算法，提出了一种新的算法。该算法结合Levenberg-Marquart算法较快的收敛性和M-Estimator算法的抗噪性，能很好地解决点数量较多和噪声点影响结果的问题。通过在 M-Estimator的权重函数上进行改进，提出自适应的权值函数，用灵活变动和自适应的值代替原来的固定值，使算法在噪声等级较高时也能表现良好。最后将算法应用在球体和圆柱上，并和最新的研究成果进行对比，数据说明算法无论是在点云数量较多还是在噪声等级较高的情况下都明显优于其他已知算法。

Levenberg-Marquart；M-Estimator；自适应权值；点云；重建

基于三维扫描点云数据的三维物体重建已经广泛地应用于计算机视觉领域，如计算机动画、医学图像处理、科学计算和虚拟现实等。在这方面存在很多优秀的算法，比如基于最小二乘法(Levenberg-Marquart, LM)算法，基于极大似然估计的M-Estimator算法和DirectFitting算法[1]。

前面两种算法都是基于迭代求解的，而最后一种算法是基于算术求解的，通过数学推导直接算出最后的结果。故在点的数量较少且没有噪声时后一种算法无论是在速度还是在准确性上都要优于迭代算法。但是一旦点的数量增加或者点云中夹杂着噪声时基于迭代求解的算法优势又体现出来了，在结果的精准性上要明显高于直接求解的算法。本文算法主要基于迭代求解，故这里重点关注前面两种算法。

一般通过迭代来解决最小二乘问题，而迭代方法中又有3种是最常用的：①最速下降法。利用方程的一阶导数逼近信息，该方法能保证迭代结果的正确性，但是不能保证迭代的速度。尤其在点的数量较多时，迭代收敛的速度非常慢。②高斯牛顿算法。其利用方程的二阶导数信息，比最速下降法有了更快的收敛速度，但是降低了迭代结果的正确性。③为了能同时解决迭代速度和结果准确性的问题，研究者们提出了LM算法[2-3]。LM算法结合了前两种算法的迭代公式，并在算法中根据前一次的迭代结果动态地决定后面的迭代是用最速下降法还是高斯牛顿法。当迭代速度变慢时，会自适应地调用高斯牛顿法来调整迭代的速度；当后一次的迭代误差比前一次还要大时，说明已经有可能偏离了正确的迭代方向，这时该算法又会自适应地调用最速下降法来调整迭代方向。这样的自适应调整不仅能保证迭代不会偏离正确的迭代方向，又能保证迭代结果的正确性。但该算法还不是最好的，因为实际应用中三维扫描得到的点云数据一般都有噪声，因为扫描设备的不同和扫描环境的不同，其结果中的噪声等级也不相同。噪声会严重影响LM算法的收敛速度和迭代结果的准确性。因此有必要对这些算法做必要的改进使得能够在处理实际数据时产生较好的结果。基于极大似然估计的M-Estimator[4-8]算子就是为了解决噪声问题提出的算法，该算法在LM算法的迭代公式中增加一个算子。在每一步迭代中该算子都会对每个迭代点产生一个权值，这个权值将决定这个点对最后的迭代结果产生多大的影响，权值越大说明对结果的影响越大，反之则越小。因为点云中有噪声点，所以如果能在迭代的过程中将噪声点的影响消除或减小，噪声就不会对迭代结果产生太大的影响。该算法在一定程度上解决了这一问题，但是在噪声等级较大或点的数量太大或太小时还是有较大的误差。经过仔细研究M-Estimator的算子发现该算子加权在每个点上的值是一个常量值，不会随着迭代的进行而动态的进行调整，因此不具有灵活性和自适应性。所以才会在噪声点较多的时候表现的不好。一些研究者也对这些问题进行了研究，李胜男等[9]提出了运用点云的球面三维逆向建模；刘进[10]运用了自适应方法进行CAD模型重建；Liu和Wu[11]通过点云进行了自适应的原始形状抽取。

针对上述存在的各种问题，本文提出了一种自适应的权值算法。M-Estimator算子在迭代的最初几步，如果给定的初始值和正确值偏离得比较远，会使得大部分的数据点都不参与计算，能参与计算的小部分点很有可能是噪声点，这样会让迭代方向出错，使程序迭代次数增加，迭代的结果也有可能出错。因此本文提出一种更加灵活的权重函数，无论是在迭代的最初几步，还是在迭代将要收敛的时候都能让足够多的正确点影响最后的迭代结果，并且排除噪声点或减小噪声点对最后迭代结果的影响。利用上一次的迭代中每个点产生的误差信息来动态的决定下一次迭代中每个点的权值，也就是说每个点的前一次迭代误差会影响到下一次的权重值。通过不停的动态调整，将噪声点的影响降到最低，从而得到较好的迭代结果。综上所述，在自适应权值算法中主要有3个创新点：

(1) 自适应权重函数能和LM算法结合的更好，算法有更快的收敛速度。

(2) 不会对给定算法的初始迭代值有很强的依赖性。

(3) 结合本文权重函数，LM算法对噪声表现出更强的鲁棒性。

1　自适应权重函数算法

1.1问题定义

在实际应用中经常需要得到一个物体的几何表达式，但又不能通过测量的方法，唯一能得到的数据就是通过三维扫描得到该物体的点云数据，并根据这些点云数据重建出物体的几何表达式。由于扫描设备的问题和环境因素的干扰，导致扫描出来的数据经常有很多噪声，在重建时还需排除这些噪声的影响，否则重建的结果将会产生很大的误差。下面对这个问题给出一个比较严格的数据定义。

i程参数。如果f表示的是一个球体，可通过某种方法求出这个球体的球心坐标和球体半径；如果f表示的是一个圆柱体，需求出圆柱体的半径和轴线的方向向量。这里f所表示的物体类型是已知的。

1.2自适应权值函数

其中，ρ是一个对称正定且在原点有唯一最小值的函数。不直接解这个问题，而是将其转换为一个迭代加权最小二乘问题。设为将要计算的未知数，也就是如下线性方程组的解：

这里的偏导数ψ(x)=dρ(x)/d x称为影响函数。式(3)定义了权重函数：

现将式(2)用式(4)表示：

式(4)正是求解最小二乘问题的线性方程组：

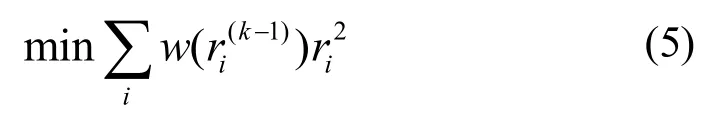
相应的影响函数ψ(x)为：

权重函数w(x)为：

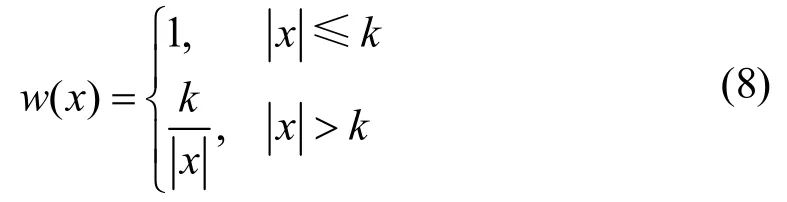
传统的算子使得最小二乘问题对噪声具有更强的鲁棒性，但因k值是一个常数使得权重函数式(8)不够灵活。在迭代的最初几步，如果给定的初始值和正确值偏离得比较远，因为k值很小使得大部分的数据点均不参与计算。在噪声点较多时，能参与计算的小部分点也很有可能是噪声点，这样会让迭代方向出错，还会使程序收敛的速度下降，并使迭代结果产生较大的误差。让k更加灵活，在刚开始迭代时让更多的正确点能参与计算，或者增大正确点对迭代结果的影响。

设ri的绝对值为所有点的误差集合，则误差绝对值的集合可表示为：

该权重函数有以下2个优点：

(1) 在迭代的最初几步确保大部分的点都能参与计算，不会产生像Huber一样的问题，这样算法就不会对初始值的设定产生很大的依赖性。

(2) 在保证大部分点都参与计算的情况下还能保证噪声点不对迭代结果产生很大的影响，由此确保结果的可信度。

将权重函数和LM算法结合就可得到如式(11)所示的计算迭代方向的表达式：

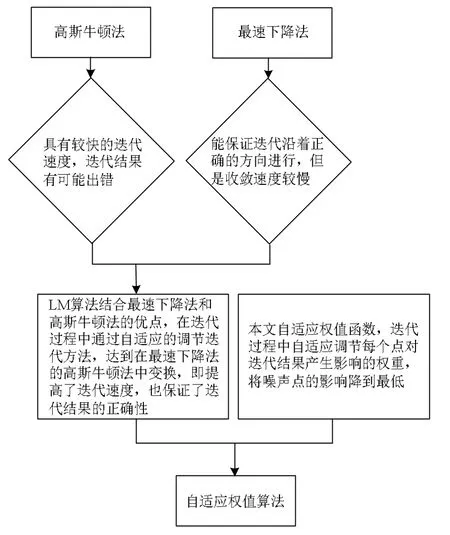
图1　算法衍生图

下面给出算法在球体和圆柱体上的实验结果，并将其结果和LM算法与M-Estimator算法进行比较。

2　实验结果

为了方便实验结果的对比，将给出圆柱体和球体2种情况的实验结果，较一般的情况同样也可以用本文算法得出较好的结果。可从几个方面进行对比。①从点的数量上进行对比，每组实验均在两组点上进行，一组点数较多，一组点数较少。②在不同的噪声等级上比较，具体来说在没有噪声和噪声等级分别为 0.2，0.5，1.0，1.5上进行比较，数值越大噪声比例越大。③因为参数较多，而且不是每个参数在各个算法中都会产生剧烈的变化，所以只对明显有不同的参数进行比较。在球体的实验中，几种算法产生的结果主要区别在球体的半径和球心坐标的Z轴上，其他的几个参数都没有明显的不同，所以不做比较；在圆柱体的实验中，实验结果的主要区别是在圆柱体的半径上，圆柱轴线方向向量没有明显区别，因此只对半径进行比较。

图2中给了两组球体半径实验结果对比，分别为点数采样比例为1和采样比例为4，前者点数较多。在两组图中给出了球体的标准值为15，如图中的水平线所示。从图中可以看出自适应权值算法在5个噪声等级上明显要好于LM算法。在点的采样比例为1噪声等级达到1.5时，LM算法得出的球体半径已经和标准值偏离了3个单位，而本文算法只和标准值差1。在噪声等级为0.2时M-Estimator的半径值和标准值达到3的差距。在两个点采样比例下，当噪声比例达到1.5时，M-Estimator算出的半径比本文算法好，这是以其他参数的大误差为代价的。从下面的球体Z轴的对比结果可以看出这点，如图3所示。

在图3中用水平线标出了5个噪声等级下的Z轴标准值都为0。LM算法和M-Estimator算法在噪声等级达到0.2后就会出现较大的误差，最大的误差达到10，而且变化剧烈，其在实际应用中是不能接受的。虽然本文算法也会有误差，但相对于另外两种算法的总体误差要小，而且变化相对较平缓，从而体现了自适应权值的效果。

圆柱体的半径实验结果对比图如图4所示。在圆柱体的实验中其圆柱体的半径标准值为15，LM算法在噪声等级高于0.2后半径就开始出现了较大的偏差，M-Estimator相对于LM算法要好，相对于本文算法要差。

图5和图6给出了更直观的比较。图5为球体标准图和3种算法计算出来的图，其噪声等级为1.0 和 0.5；标准图形球心为(0,0,0)，半径为 15。从两个图的分离程度可看出算法的误差，其中本文算法与标准图吻合最好。

图6为圆柱体标准图和3种算法实验结果图，其噪声等级为1.0和0.5；标准图形轴向均为(0.866, 0.499, 0)，轴线过(0, 0, 0)，半径为15。从两个图的分离程度可以看出本文算法的精度好于LM算法和Huber算法。

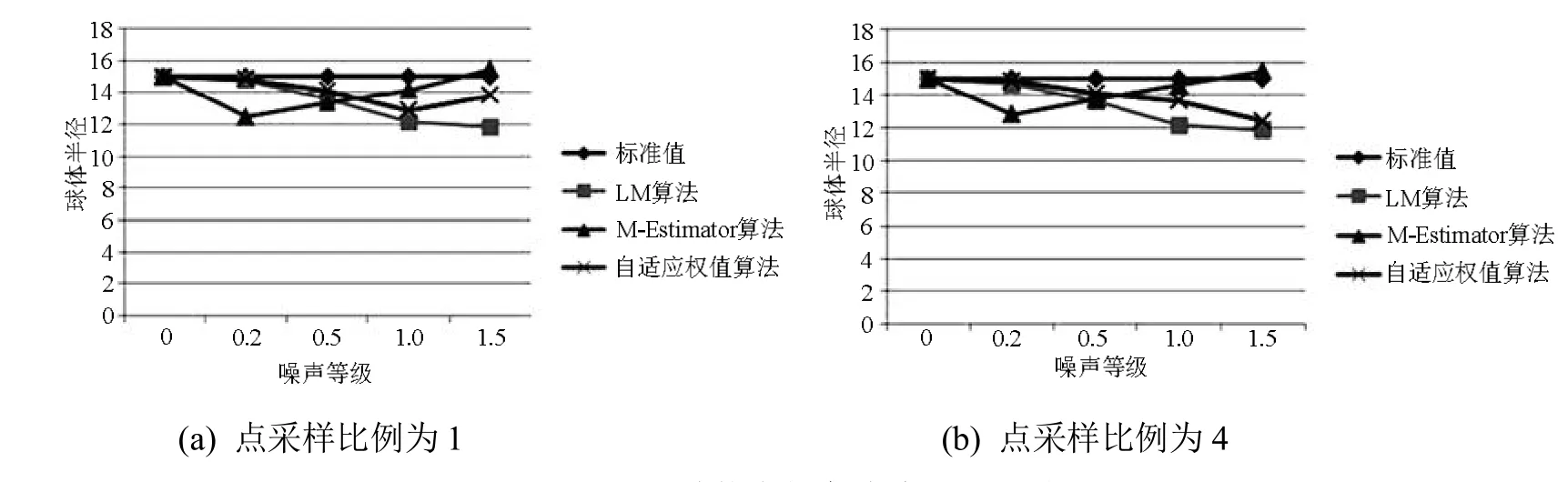
图2　球体半径实验结果对比图

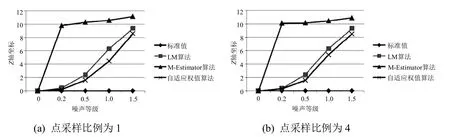
图3　球体Z轴实验结果对比图

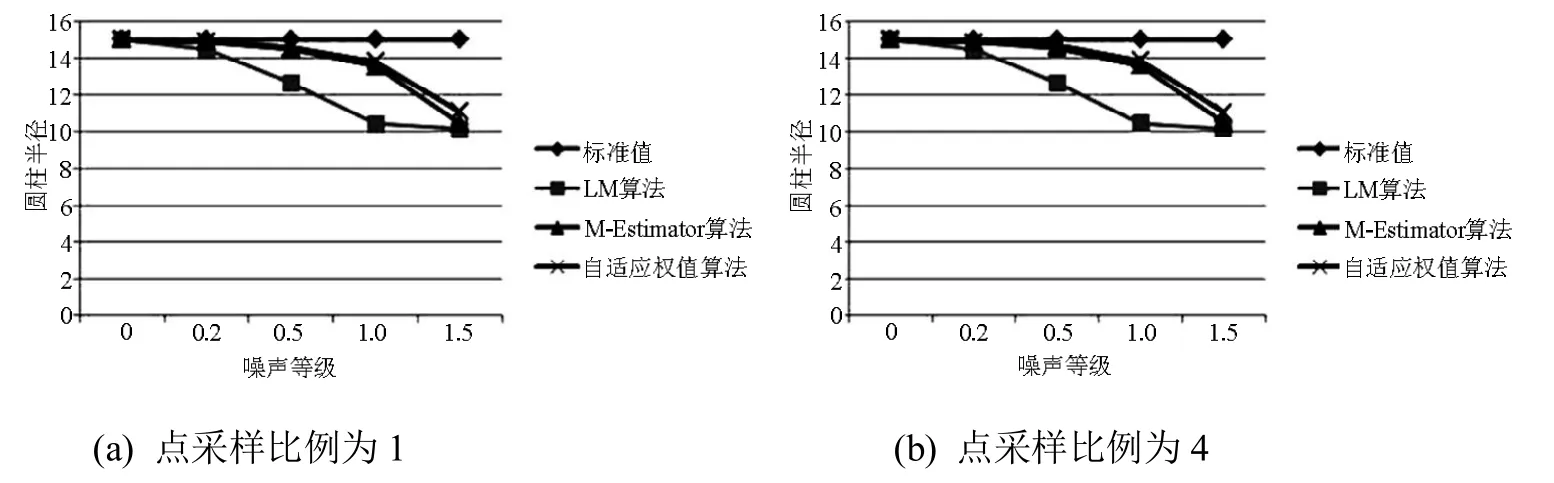
图4　圆柱体半径实验结果对比图

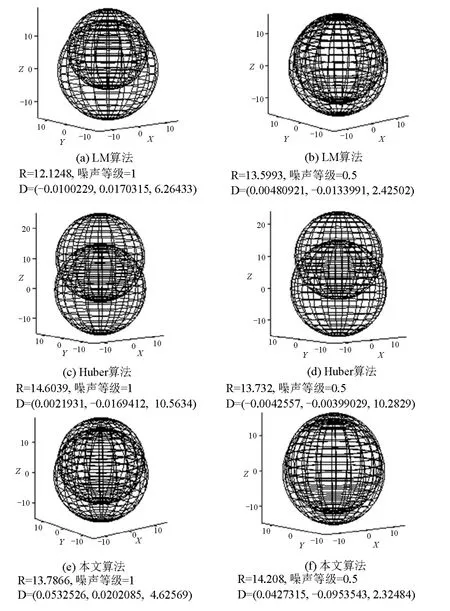
图5　球体上的实验结果对比

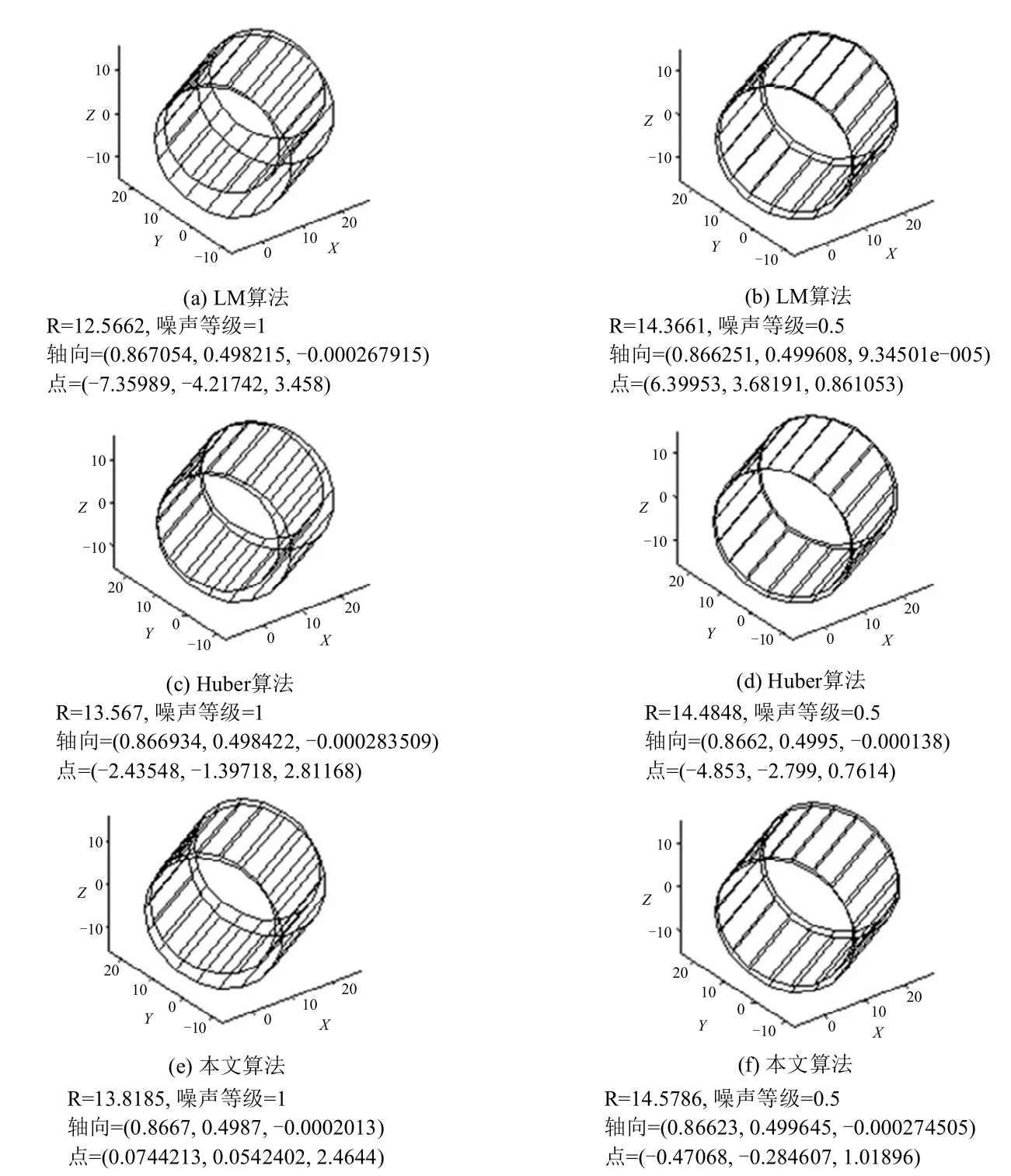
图6　圆柱体上的实验结果对比

3　总　结

三维点云的重建在计算机视觉领域有很多的应用，如计算机动画、医学图像处理等。从有噪声的数据中重建出原始物体的模型是项艰巨的任务，虽然有很多算法，但是这些算法对噪声的鲁棒性不是很好，基于此提出了自适应权值算法。将自适应权值函数和LM算法结合起来能对有噪声的点云进行很好地重建。权重函数在每次迭代时能动态地调整自己对每个点的权重值，从而调整每个点对迭代结果的影响权重，达到自适应调整的目的。通过这样的自适应调节能更好地排除或减小噪声的影响，从而达到较好的迭代结果。

通过实验对比，发现本文算法无论是对较简单的物体还是复杂的物体都能较好地重建。无论是在速度、还是在精度上都比其他两种算法要好。但是本文算法在性能上的提升不是很明显，未来的工作将专注于性能的提升和改进。

[1] Shah T R. Automatic Reconstruction of Industrial installations using point clouds and images [D]. Shanghai: Shanghai Jiao tong University, 2006.

[2] Shakarji C M. Least-squares fitting algorithms of the nist algorithm testing system [J]. Journal of Research of the National Institute of Standards and Technology, 1998, 103(6): 633-641.

[3] Ranganathan A. The levenberg-marquardt algorithm [J]. Tutoral on LM Algorithm, 2004, 11(1): 101-110.

[4] Zhang Z Y. Parameter estimation techniques: a tutorial with application to conic fitting [J]. Image and Vision Computing Journal, 1997, 15(1): 59-76.

[5] Bustos O H, Lucini1 M M, Frery A C. M-Estimators of roughness and scale for-modelled SAR imagery [J]. EURASIP Journal on Applied Signal Processing, 2002, 1: 105-114.

[6] Tyler D E. A distribution-free M-Estimator of multivariate scatter [J]. The Annals of Statistics, 1987, 15(1): 234-251.

[7] Smolic A, Ohm J R. Robust global motion estimation using a simplified M-Estimator approach [J]. Image Processing, 2000, 1: 868-871.

[8] Clark D I, Osborne M R. Finite algorithms for Huber’s M-Estimator [J]. Society of Industrial and Applied Mathematics, 1986, 7(1): 72-85.

[9] 李胜男, 林晓, 陈言, 等. 基于点云的球面三维逆向建模[J]. 图学学报, 2013, 34(3): 49-52.

[10] 刘进. 自适应的基于点云的 CAD模型重建方法[J].计算机应用, 2013, 33(9): 2617-2622.

[11] Liu J, Wu Z K. An adaptive approach for primitive shape extraction from point clouds [J]. Optik-International Journal for Light and Electron Optics, 2014, 125(9): 2000-2008.

Point-Cloud 3D Object Reconstruction by Using Adaptive Weighting Function

Lin Xiao1,2,Wang Yanling2,Zhu Hengliang3,Hu Ganle3,Ma Lizhuang3,Li Luqun1

(1. The College of Information, Mechanical and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China; 2. Academy of Information Technology, Luoyang Normal University, Luoyang Henan 471022, China; 3. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

3D object reconstruction based on point clouds is an important field in computer graphics which have been used in computer animation, medical image processing and so on. Many good algorithms have been developed to solve this problem such as Levenberg-Marquart algorithm based on least squares and M-Estimator based on maximum likelihood estimation. But all of these algorithms are sensitive to noise and the data number of too lager or too little. And the result of these algorithms would have a larger error, which can influence the effect of reconstruction. In order to solve these problems, we propose a new algorithm which is based on Levenberg-Marquart algorithm and M-Estimator. Our algorithm takes advantage of high convergence of Levenberg-Marquart algorithm and noise proof of M-Estimator, so it can solve two problems mentioned above. And we improved the weighting function of M-Estimator which replaces the constant value with the flexible and adaptive value. This way makes our algorithm to behave very well in large number of points andhigh level of noise. We apply our algorithm on ball and cylinder and compare with the latest research results. From the experimental data we can see that our algorithm behaves much well than the others.

Levenberg-Marquart; M-Estimato; adaptive weighting function; point cloud; reconstruction

TP 391

10.11996/JG.j.2095-302X.2016020143

A

2095-302X(2016)02-0143-06

2015-09-24；定稿日期：2015-10-22

国家自然科学基金项目(U1304616, 61502220)

林晓(1978–)，女，河南南阳人，副教授，博士。主要研究方向为图形图像、数字媒体与数据重建。E-mail：lin6008@126.com

李鲁群(1967–)，男，山东泰安人，教授，博士。主要研究方向为移动GIS、数字媒体等。E-mail：liluqun@gmail.com