基于差分进化算法的B样条曲线曲面拟合

何兵朋， 冯仁忠， 余胜蛟

(北京航空航天大学数学与系统科学学院，北京 100083)

基于差分进化算法的B样条曲线曲面拟合

何兵朋， 冯仁忠， 余胜蛟

(北京航空航天大学数学与系统科学学院，北京 100083)

应用B样条曲线曲面拟合内在形状带有间断或者尖点的数据时，最小二乘法得到的拟合结果往往在间断和尖点处误差较大，原因在于最小二乘法将拟合函数B样条的节点固定。本文在利用3次B样条曲线和曲面拟合数据时，应用差分进化算法设计出一种能够自适应地设置B样条节点的方法，同时对节点的数量和位置进行优化，使得B样条拟合曲线曲面在间断和尖点处产生拟多重节点，实现高精度地拟合采样于带有间断或尖点的曲线和曲面数据。

数据拟合；B样条曲线曲面；最小二乘法；差分进化算法；自适应；拟多重节点

B样条曲线曲面已被广泛应用于数据拟合、几何建模、CAD、医学成像等领域[1-4]。当拟合数据的内在形状较为复杂时，简单的多项式难以精确地拟合，然而具有局部可调性质的B样条是一种有效的拟合函数。节点的设置对B样条曲线的形状有重要的影响，不合理的节点矢量可能会产生不可接受的形状[5-6]。所以，应用 B样条进行数据拟合的关键在于寻找最优的节点矢量，包括节点的数量和位置。节点设为变量的B样条拟合问题是一个多元和多极值的非线性最优化问题[7]，难以获得其全局最优解且最小二乘法无法直接求解此类问题。鉴于此，许多传统的方法[8-10]被提出来，这些方法可分为2类：节点插入和节点删除，如Jupp[9]提出一种将节点进行对数转化的方法；Lyche和Mørken[8]提出一种数据简化算法实现节点删除的方法。近年来，许多异于上述传统方法的自适应设置节点的算法被提出[5-6, 11-13]，如Yoshimoto等[11]提出一种基于遗传算法的自适应地优化节点数量和位置的方法，能够较好地拟合带有尖点和间断的数据；Li等[5]提出一种基于数据点的光滑曲率和启发式准则的非迭代算法，较好拟合稠密的和带噪音的数据点；Ülker和İşler[12]提出一种人工免疫系统方法以求解B样条曲面拟合问题。然而，很多文献只是将提出的方法用于B样条曲线拟合，并没有将其扩充到B样条曲面拟合。

本文应用差分进化算法[14](differential evolution, DE)设计出一种新的求解B样条拟合的方法，其能够根据数据的变化情况自适应地设置节点，同时对节点的数量和位置进行优化，并且在间断和尖点处产生拟多重节点。通过计算机程序计算浮点型节点产生真正的多重节点是几乎不可能的，但是通过数值试验发现，本文提出的方法能够产生多个非常接近的节点，可称之为拟多重节点。拟多重节点使得拟合曲线能较好地拟合急剧变化的数据，包括间断和尖点。

从对比数值试验的结果可发现，本文提出的方法的拟合效果比最小二乘法和遗传算法都要好，能更精确地求解采样于带有间断和尖点函数数据的B样条曲线曲面拟合问题。

1　基于最小二乘法的B样条拟合

以二维数据拟合为例，介绍B样条拟合的最小二乘法。假设拟合数据为：

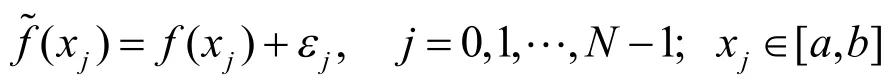
其中，f(x)为采样函数(对于散乱数据，f(x)是未知的)，ε为噪音误差，N为采样数量。

设定义k次B样条曲线的节点为ξi∈[a,b] (i=0,1,…,n+2 k +1)，n为内节点数。通常将端节点设为k+1重节点，即：

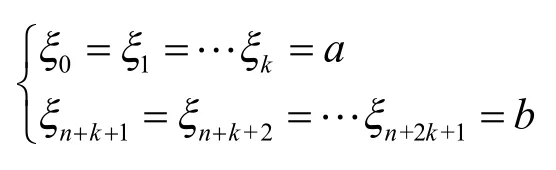
拟合函数记为：

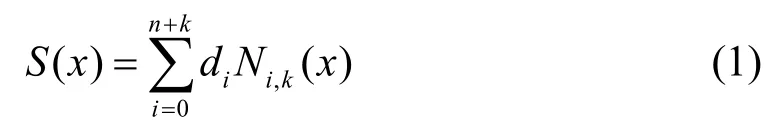
其中，di(i=0,1,…,n+ k)为控制顶点，Ni,k( i=0,1,…,n+ k) 为k次B样条基函数，其递推公式为：

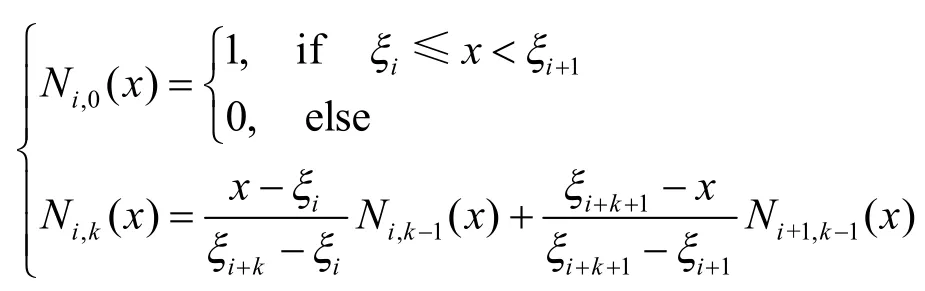
用R记以下残差平方和：

2　基于差分进化算法的B样条拟合

最小二乘法是在 B样条的内节点数量和位置均固定的情况下求得最优拟合曲线或曲面，以致其对间断和尖点的拟合效果较差。本文在最小二乘法的基础上，应用差分进化算法设计出一种能够根据拟合数据的变化情况自适应地设置 B样条节点的方法，同时对节点数量和位置进行优化，从而更精确地拟合急剧变化的数据。

2.1B样条拟合的差分进化算法实现

(1) 初始种群。在差分进化算法中将优化问题的一个可行解作为一个个体，在这里将B样条拟合问题中的一组可行内节点(ni为ξi的长度)作为一个个体，由NP个个体组成一个种群，NP称为种群规模。本文中初始种群个体长度均设为L=[λN]，N是被拟合数据点数量，λ称为节点率，其取值随具体实例的不同而改变。

本文在差分进化算法的变异和杂交操作的基础上增加删除和插入节点功能，来自适应地调整内节点的数量和位置。对第G代的第i(i=0,1,…,NP-1)个个体进行变异、杂交和选择操作。

(2) 变异操作。变异操作分3步来完成。

步骤1. 随机选取 3个互不相同且不同于ξi,G的个体,分别对进行如下操作：

如果rand()1＜dp(dp称为删除概率，rand()1为[0,1]之间的随机数)，则随机删除ξj,G中的一个节点，得到一个新个体ξ′j,G；否则，按升序向ξj,G随机插入一个(a,b)之间的节点，得到一个新个体。

步骤2. 取D=m in{nr1,nr 2,nr 3}，其中nr1,nr 2,nr 3分别为的长度。如果D=nr 1，则将中每nr2-D+1个元素相加后求其平均值按顺序依次存入 ξr′2,G中，即：

同样地，对ξr′3,G进行此操作。如果D=nr或D=nr3时，同样依此方法处理。

其中，FG称为变异系数，本文其值取为，Gm为最大迭代次数。

(3) 杂交操作。将ξi,G和Ui,G杂交得到试验向量Vi, G：

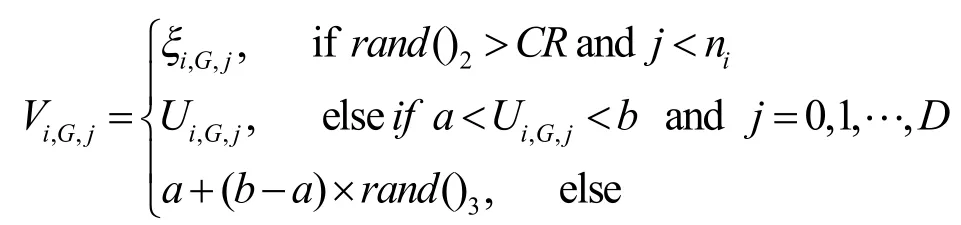
(4) 选择操作。本文使用统计学中贝叶斯信息准则 BIC[15](评价模型拟合效果的一种方法)作为适应度函数，在本文曲线拟合问题中，其表达式为：

其中，N为拟合数据点的数量，R为残差平方和，2n+k+1为变量的数量。曲面拟合问题中，其表达式类似给定。BIC值的大小反映了拟合精度，其值越小，拟合精度越高。

选择操作过程：首先对个体ξi,G通过第 1节中最小二乘法求得对应的B样条最优控制顶点；然后利用式(2)求出相应的残差平方和R，进而利用式(3)计算出与ξi,G对应的适应度函数值ξ_BIC。同时，采用同样的方法计算出与Vi,G对应的适应度函数值V_BIC。最后，根据贪婪法则，选择较优个体遗传到下一代：

2.2数据拟合算法

结合上述差分进化算法的描述，给出以下数据拟合算法：

步骤2. 输入差分进化算法参数，包括种群规模NP、节点率λ、节点删除概率dp、最大迭代次数Gm；

步骤4. 对每一个个体应用最小二乘法求得与之对应的最小残差平方和，进而计算出对应的适应度函数BIC值；

步骤5. 进行变异和杂交操作；

步骤6. 根据适应度函数值进行选择，并更新种群；

步骤7. 判断迭代终止条件G＞Gm。如果达到终止条件，则停止计算，输出最优内节点组；否则，转到步骤4。

3　数值试验

利用第1～2节介绍的算法，对几组采样于带有间断、尖点以及间断面的曲线和曲面数据进行拟合，将拟合结果与遗传算法的结果及最小二乘法拟合结果进行比较。

3.1曲线拟合

例1. 拟合数据由以下函数生成：

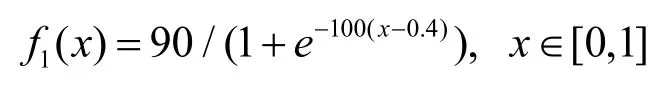
该函数在x=0.4附近发生剧烈的变化，其形状类似于一个台阶。相关参数设置：λ=0.025，dp=0.6。

图1、2为每一代最优个体的适应度函数值以及内节点数量随迭代次数的增加而变化的图像，其中点划线表示 30次试验的平均适应度函数值随迭代次数的增加的变化图像，实线表示 30次试验中最好的一次试验的适应度函数值随迭代次数的增加的变化图像，点线表示内节点数随迭代次数的增加的变化图像。从图1可看出，DE算法大概在25代收敛，且收敛结果稳定；内节点数很快由初始给定的5个减少为4个，并保持不变；DE算法收敛后适应度函数值为630，大约为遗传算法同等条件下的收敛值1 200的一半。这反映了本文方法的拟合精度高于遗传算法。

将最小二乘法拟合效果和本文提出的算法收敛时的拟合效果进行了对比，图3为5个均匀分布内节点的B样条的最小二乘法拟合效果图，图4为差分进化算法收敛后的拟合效果图。通过两图对比可看出，在x=0.4附近，最小二乘法得到的3次B样条拟合曲线出现较大的波动，拟合效果较差，而差分进化算法得到的3次B样条拟合曲线在此处附近与采样数据点相合较好，其拟合效果明显优于最小二乘法。原因在于差分进化算法能对内节点的位置和数量进行优化，节点由初始均匀分布的5个，优化为汇集在x=0.4附近的4个，并在x=0.4处产生一个拟二重节点，提高了拟合精度。

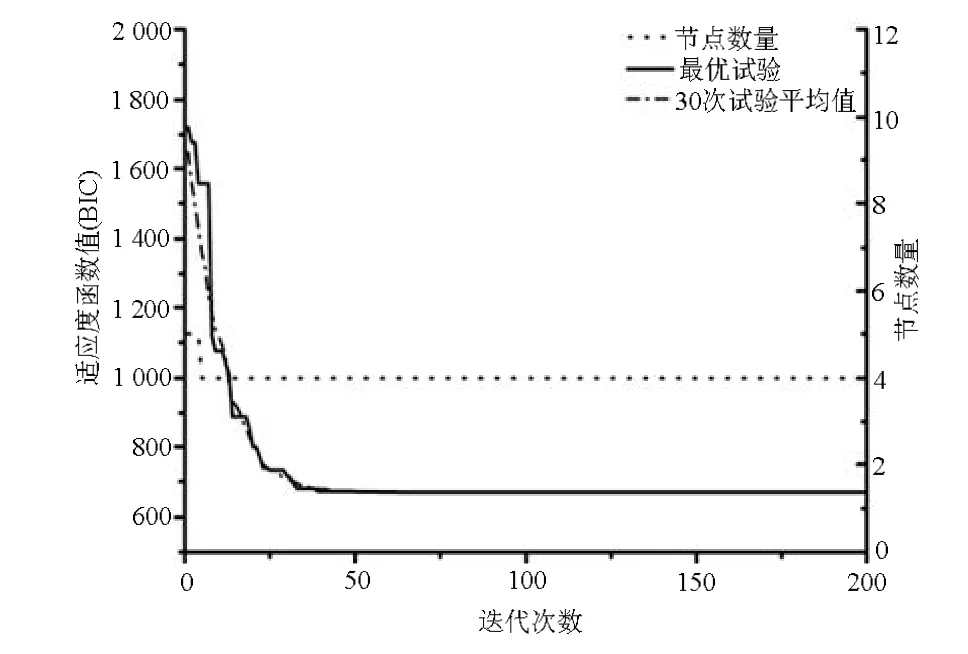
图1　DE算法适应度函数值以及节点数变化图像

图2　遗传算法适应度函数值以及节点数变化图像

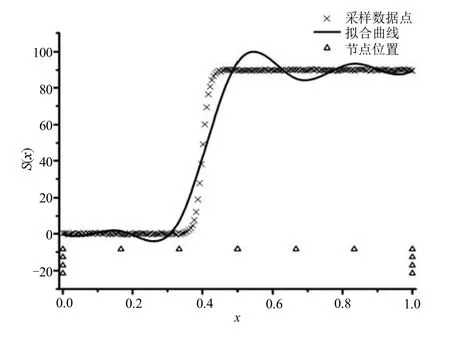
图3　最小二乘法拟合效果图

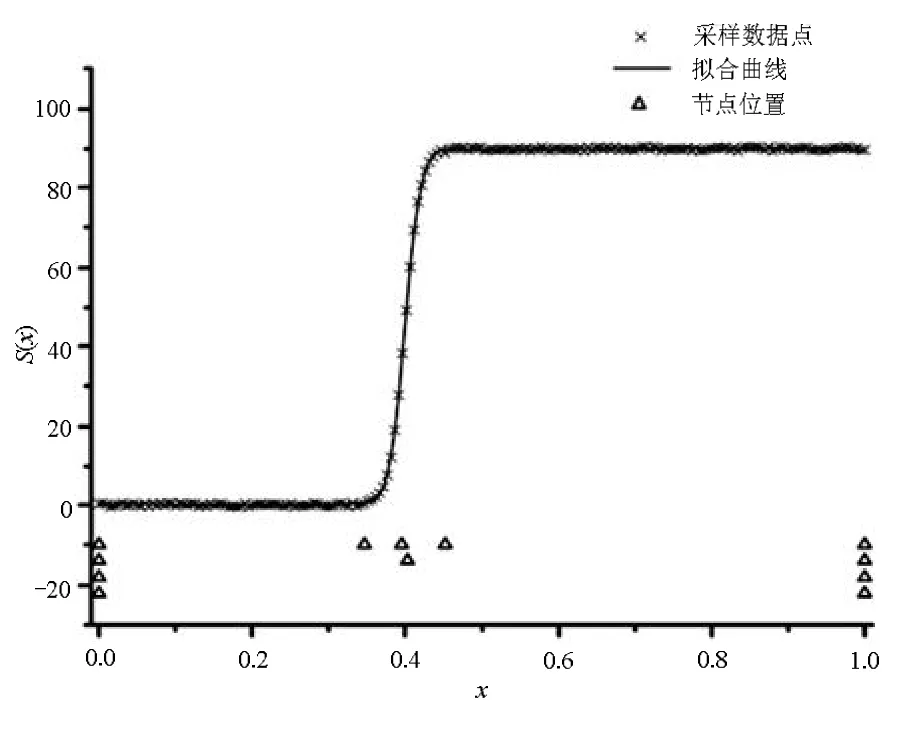
图4　DE算法拟合效果图

例2. 拟合数据由以下函数生成：

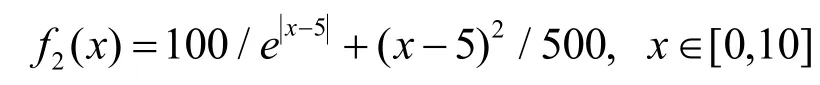
该函数在x=5处不可导，有一个尖点。相关参数设置为：λ=0.05，dp=0.6。

由图5可知，DE算法大概在75代收敛，收敛结果稳定；内节点数很快由初始给定的10个减少为7个，并保持不变；对比图5和图6，DE算法收敛后适应度函数值为640，大约为遗传算法的计算结果1 200的一半。对比图7、8易知，差分进化算法收敛后冗余的节点被删除，并且在尖点处产生了一个拟三重节点；在尖点 x=5附近，最小二乘法得到的3次B样条拟合曲线是光滑的，拟合效果较差，而差分进化算法对节点数量和位置进行优化后得到的拟合曲线几乎与采样点重合，拟合效果较好。

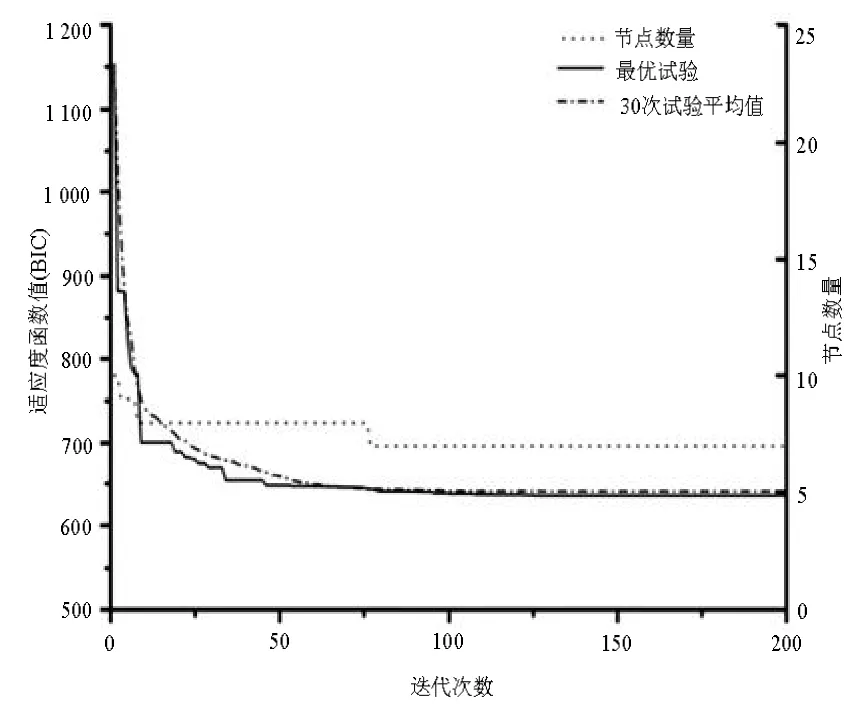
图5　DE算法适应度函数值以及节点数变化图像

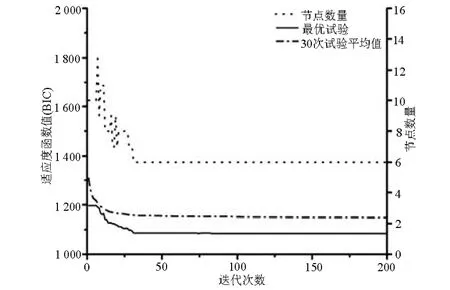
图6　遗传算法适应度函数值以及节点数变化图像

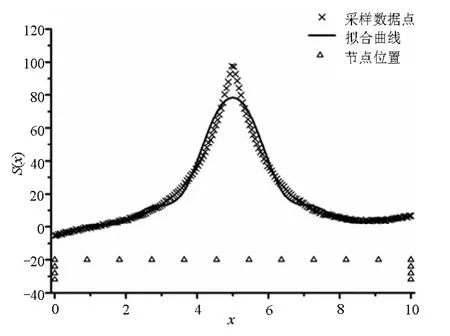
图7　最小二乘法拟合效果图

图8　DE算法拟合效果图

3.2曲面拟合

应用提出的方法对表1中2个带有间断或尖点的曲面进行拟合。曲面拟合数值试验：均取32×32的网格进行无噪音数据采样；均通过均匀节点加随机扰动的方法生成初始种群；差分进化算法参数均设置为NP=50，Gm=2 000；终止条件均设为：平均平方误差MSE＜10-5或者迭代次数 G＞Gm。MSE的定义为：

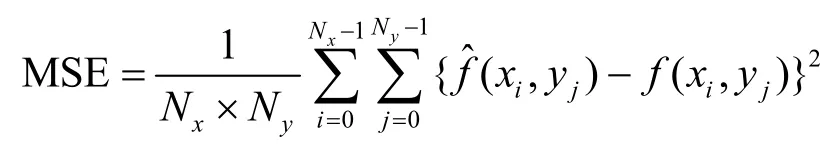
表1　测试函数

表2　曲面拟合数值试验计算结果

由表2可知，与初始时节点数量相比，DE算法收敛后测试1节点的数量减少了，而测试2节点数量增加了，这说明本文提出的方法实现了节点自适应设置。

将差分进化算法收敛后的拟合效果与最小二乘法拟合效果进行对比。图9为按照表2设置的初始均匀分布内节点的情况下最小二乘法拟合效果图和差分进化算法收敛后的拟合效果图。比较图9(a)～(b)可知，最小二乘法得到的拟合曲面在间断处是光滑的且有振荡，拟合效果较差；而差分进化算法收敛后得到的3次B样条拟合曲面几乎能准确构造出采样数据曲面。比较图9(c)～(d)可知，最小二乘法拟合结果在图形底部有较大的误差，而差分进化算法收敛后拟合结果较好重构出被拟合函数的图像。

图9　曲面拟合数值试验效果图

4　结论与展望

本文利用差分进化算法设计了一种求解3次B样条曲线曲面非线性拟合问题的方法，该方法能够自适应地优化内节点的数量和位置，在间断和尖点附近产生拟多重节点，实现了对带有间断和尖点的曲线曲面高精度拟合。通过数值试验发现，迭代过程中误差呈台阶式下降。此外，本文提出的方法对不同的实例需要通过试验来确定节点删除概率的大小。鉴于此，作者将进一步研究差分进化算法和本文提出的方法，加快算法收敛速度，实现参数对不同实例的自适应调整。

[1] Safari A, Lemu H G, Jafari S, et al. A comparative analysis of nature-inspired optimization approaches to 2D geometric modeling for turbomachinery applications [J]. Mathematical Problems in Engineering, 2013, (11): 1-15.

[2] 冯仁忠, 查理. 局部构造C2连续的三次B样条插值曲线和双三次插值曲面[J]. 工程图学学报, 2005, 26(6): 110-117.

[3] Lee D, Pavlidis T. One-dimensional regularization with discontinuities [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1988, 10(6): 822-829.

[4] Zhao X Y, Zhang C M, Xu L, et al. IGA-based point cloud fitting using B-spline surfaces for reverse engineering [J]. Information Sciences, 2013, 245(10): 276-289.

[5] Li W S, Xu S H, Zhao G, et al. Adaptive knot placement in B-spline curve approximation [J]. Computer-Aided Design, 2005, 37(8): 791-797.

[6] Zhao X Y, Zhang C M, Yang B, et al. Adaptive knot placement using a GMM-based continuous optimization [J]. Computer-Aided Design, 2011, 43(6): 598-604.

[7] Dierckx P. Curve and surface fitting with splines [M]. Oxford: Oxford University Press, 1993: 58-61.

[8] Lyche T, Mørken K. A data-reduction strategy for splines with applications to the approximation of functions and data [J]. Ima Journal of Numerical Analysis, 1988, 8(2): 185-208.

[9] Jupp D L B. Approximation to data by splines with free knots [J]. SIAM Journal on Numerical Analysis, 1978, 15(2): 328-343.

[10] Piegl L, Tiller W. The NURBS book [M]. New York: Springer Press, 1997: 141-187.

[11] Yoshimoto F, Harada T, Yoshimoto Y. Data fitting with a spline using a real-coded genetic algorithm [J]. Computer-Aided Design, 2003, 35(8): 751-760.

[12] Ülker E, İşler V. An artificial immune system approach for B-spline surface approximation problem [C]//Lecture Notes in Computer Science. Berlin: Springer Press, 2007: 49-56.

[13] Garcia-Capulin C H, Cuevas F J, Trejo-Caballero G, et al. Hierarchical genetic algorithm for B-spline surface approximation of smooth explicit data [J]. Mathematical Problems in Engineering, 2014, 2014: 1-11.

[14] Storn R, Price K. Differential evolution: a simple and efficient adaptive scheme for global optimization over continuous spaces [J]. Journal of Global Optimization, 1995, 23(4): 341-359.

[15] Schwarz G B. Estimating the dimensions of a model [J]. The Annals of Statistics, 1978, 6(2): 461-464.

B-Sp line Curve and Surface Fitting Using Differential Evolution A lgorithm

He Bingpeng,Feng Renzhong,Yu Shengjiao

(School of Mathematics and System Science, Beihang University, Beijing 100083, China)

To use B-spline curve and surface to fit data with an underlying function having discontinuous points and/or cusps, the fitting results obtained by least squares method are often bad in the vicinity of discontinuous points and cusps because of the fixed B-spline knots. In this paper, we propose a method for solving data fitting problem with cubic B-spline curve and surface by using differential evolution algorithm. Our method can set B-spline knots adaptively, so as to optim ize the number and location of knots simultaneously and produce quasi-multiple knot in the vicinity of discontinuous points and cusps. W ith this, we can fit data with an underlying function having discontinuous points and/or cusps with high precision.

data fitting; B-spline curve and surface; least squares method; differential evolution algorithm; adaptation; quasi-multiple knot

TP 391.7

10.11996/JG.j.2095-302X.2016020178

A

2095-302X(2016)02-0178-06

2015-09-24；定稿日期：2015-10-01

国家自然科学基金项目(11271041)；民用飞机专项项目(M J-F-2012-04)

何兵朋(1993–)，男，湖北咸宁人，硕士研究生。主要研究方向为计算几何。E-mail：hebinpeng429@126.com

冯仁忠(1967–)，男，江西都昌人，教授，博士。主要研究方向为数值逼近与计算几何。E-mail：fengrz@buaa.edu.cn