基于Abaqus的高强材料连接金具接触问题分析

李俊辉， 徐光辉， 常林晶， 宋铁创， 万少婷， 许爱斌

(1. 平高集团有限公司，河南 平顶山 467001；2. 北京云道智造科技有限公司，北京 100083)

基于Abaqus的高强材料连接金具接触问题分析

李俊辉1， 徐光辉1， 常林晶1， 宋铁创1， 万少婷2， 许爱斌2

(1. 平高集团有限公司，河南 平顶山 467001；2. 北京云道智造科技有限公司，北京 100083)

接触问题是一种高度非线性行为，且不同的接触类型及控制因素对仿真模型的计算结果有着重要影响。采用Abaqus软件对高强材料连接金具在使用过程中抵抗极限载荷的能力进行了非线性静力仿真分析，通过对连接金具U型挂环与其连接件间接触类型的不同设置，对比分析不同接触类型下的计算结果，明确了U型挂环在给定工况下适合的接触类型。并根据U型挂环的变形与应力分布规律，提出了相应的改进建议，为连接金具的结构设计提供了更加科学的指导。

连接金具；非线性；接触；有限元仿真

接触问题的研究很早就引起了人们的重视。早在1882年， Herz就较系统地研究了弹性体的接触问题，并提出经典的 Herz接触理论，随着数值解法的兴起和发展，出现了很多求解接触问题的非经典方法，有限元作为解决复杂工程问题最有效的数值方法，也成为求解接触问题的一种主要方法[1-3]。

随着 CAE技术的迅速发展，有限元法被广泛应用到连接金具设计中，通过仿真找到连接金具的薄弱环节而进行结构改进，相比传统的设计方法(主要依靠工程师的经验和试验结果)，不仅大大节省了人力、物力，还缩短了产品的研发周期。但是，大部分连接金具在仿真分析过程中通常都涉及到接触问题，接触类型设置的正确与否直接影响计算结果的准确性。

通常对连接金具 U型挂环与其连接件间接触类型的设置有2种：①假定U型挂环与其连接件之间相对滑移较小，可忽略不计，故将接触类型设置为绑定接触，这种接触形式具有求解速度快、容易收敛的优点。如果将两个面设置为绑定接触，相当于人为地将两个接触面上的单元“粘在一起”，这样易出现虚假应力与位移。②更倾向于将接触类型假设为面面接触，其在计算中会产生大量的迭代步，从而对计算资源要求较高且计算时间比绑定接触要长的多，同时也易出现不收敛问题。

本文利用 Abaqus软件，在考虑材料非线性基础上，对连接金具U型挂环与其连接件间分别设置为绑定接触和面面接触，进行求解计算，对比不同接触类型下的计算结果，明确U型挂环在给定工况下适合的接触类型，以期得到更加准确的接触设置方式，提高仿真精度，为连接金具的结构设计提供更加科学的指导。

1　接触理论基础

非线性问题可以分为3类：几何非线性、材料非线性和边界非线性[4-5]。接触问题是最常见的边界条件非线性，可划分为2种形式[6-7]：

(1) 依据接触类型。①刚体-柔体的接触。其是一种软材料和一种硬材料接触时，问题可以被假定为刚体-柔体的接触。②柔体-柔体的接触。其是一种更普遍的接触形式，两个接触体都是变形体。

在本文的分析中由于两连接部件的材料性能相近，而且同时受力并同时产生变形，所以是柔性体-柔性体的接触形式。

(2) 依据接触方式。可分为共形面(即两相互接触面的几何形态完全相同，处处粘合)相接触和异形曲面相接触。

本文研究的是异形曲面相接触的情况。

Abaqus/Standard采用New ton-Raphson方法进行迭代分析，将一个分析步分解为多个增量步，在每个增量步开始时检查所有接触相互作用的状态，以建立从属节点是开放还是闭合。在图1中，P表示从属节点上的接触压力；h表示从属节点侵入主控表面的距离。如果一个节点是闭合的，那么Abaqus/Standard要确定其是处于滑动还是粘结。首先Abaqus/Standard对每个闭合节点施加一个约束，而对那些改变接触状态从闭合到开放的任何节点解除约束。然后Abaqus/Standard进行迭代，并利用计算的修正值来更新模型的构形。

如果在当前的迭代步中检测到任何接触变化，Abaqus/Standard标识其为严重不连续迭代(severe discontinuity iteration)，并不再进行平衡检验，每当一个严重不连续迭代发生时，Abaqus/Standard重新将内部平衡迭代计数器设置为零。如果严重不连续迭代的数目很多，并只有很少的平衡迭代，那么Abaqus/Standard难以确定合适的接触状态。对于任何需要严重不连续迭代超过了一定的增量步，Abaqus/Standard会默认地放弃，而应用更小的增量尺度再次进行增量步计算。如果这里没有严重不连续迭代，从一个增量步到下一个增量步的接触状态不会发生改变。

因仿真过程中涉及到接触问题，计算中会产生大量的迭代步，从而对计算资源要求较高且计算时长比不考虑接触的模型要长的多，同时对于收敛问题不易把控。

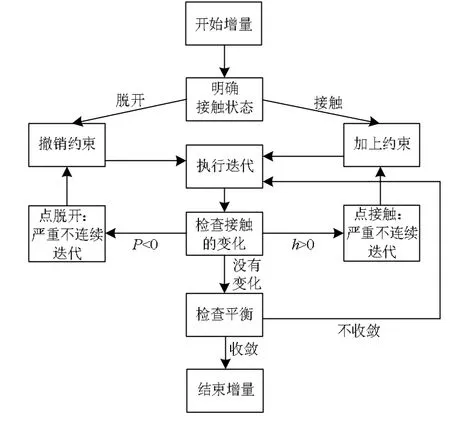
图1　接触逻辑

2　计算模型

2.1三维实体模型建立

根据初步设计的二维图纸绘制 U型挂环的实体模型(图2)。

图2　U型挂环实体模型

2.2有限元网格划分

本文利用前处理软件HyperMesh，对三维实体模型进行有限元网格剖分，根据其结构特征，U型挂环采用精度较高的四面体单元，单元数为46 981。

3　仿真计算

3.1材料特性

本文考虑材料非线性，U型挂环材料选用35CrMo。35CrMo是一种合金结构钢，具有很高的静力强度及冲击韧性，其材料参数如表1所示，材料应力应变曲线如图3所示。本文设定当U型挂环所受最大应力达到极限强度1 100 MPa后，应力值随应变量的增大而保持1 100 MPa。

表1　材料参数

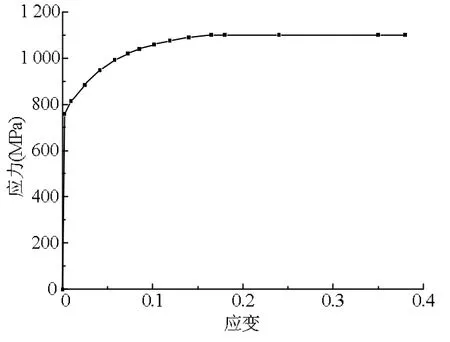
图3　材料应力应变曲线

3.2接触条件

(1) 绑定接触。在工程应用中，U型挂环通常一端用螺栓或螺杆固定，U型环端与另一U型连接件挂接而承受拉力(图4)。在拉伸过程中，U型挂环与连接件之间存在较小的相对滑移，考虑到计算资源的节省，本文对此小滑移忽略不计，将接触类型设置为绑定接触。

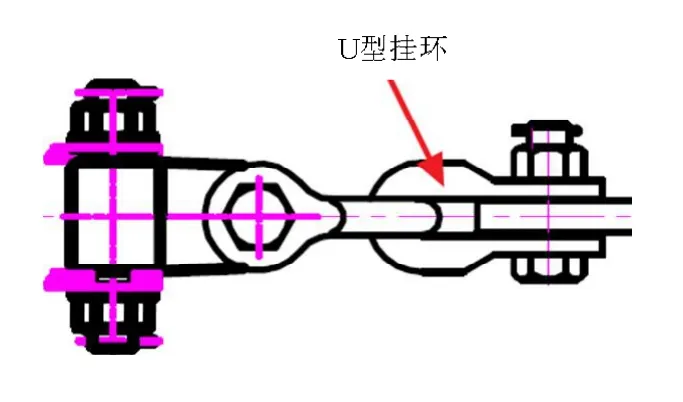
图4　U型挂环安装示意图

(2) 面面接触。在拉伸过程中，挂板与螺杆通过上侧曲面接触，且面与面之间存在较小的相对滑移，本文考虑此相对滑移对两接触部件的影响，将接触类型设置为面面接触。

3.3边界条件

为有效模拟 U型挂环的实际拉伸情况，对 U型挂环螺栓孔进行约束处理，约束连接件下侧截面除Y向平动外的所有自由度(图5)。

图5　U型挂环边界条件

3.4载荷

在 U型挂环另一侧的连接件端面处施加静力载荷(图 6)，载荷采用随时间缓慢增加的方式，以模拟随着载荷的增大，U型挂环从弹性变形到塑性变形的变化过程。另外，根据企业要求，施加的最大载荷为设计载荷(640 kN)的1.2倍，故连接件端面处施加的最大载荷为768 kN，单侧截面施加的最大载荷为384 kN。

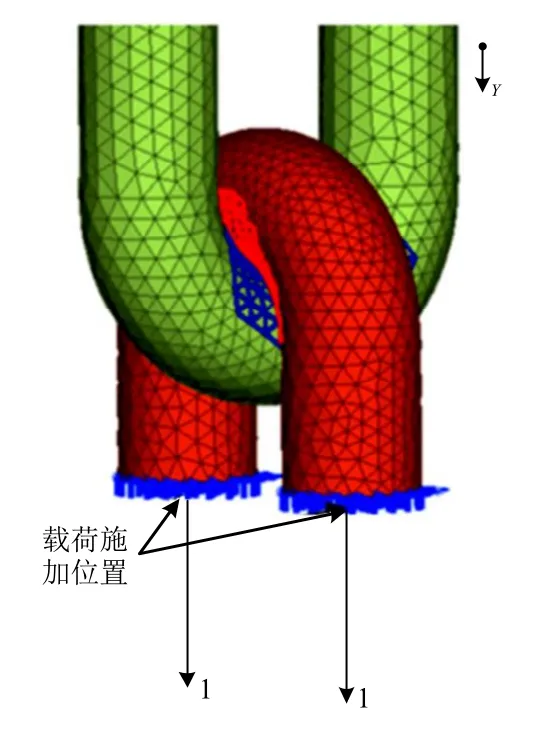
图6　U型挂环载荷施加位置

4　计算结果与讨论

4.1绑定接触计算结果

采用Abaqus/Standard，U型挂环绑定接触的计算结果如图7～10所示。

图7　绑定接触下的位移-载荷曲线

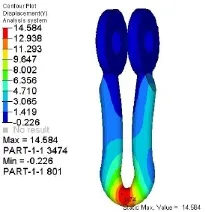
图8　绑定接触下的变形云图

图9　绑定接触下的应力云图

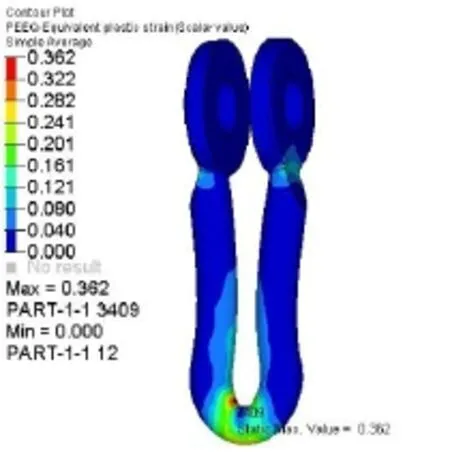
图10　绑定接触下的塑性应变云图

4.2面面接触计算结果

采用Abaqus/Standard，U型挂环面面接触计算结果如图11～14所示。

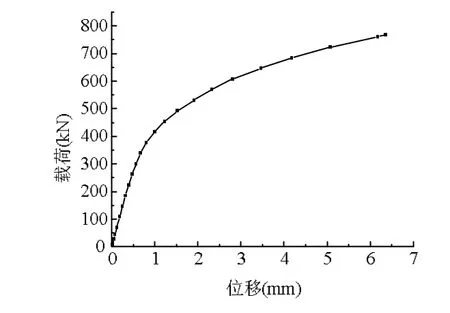
图11　面面接触下的位移-载荷曲线

图12　面面接触下的变形云图

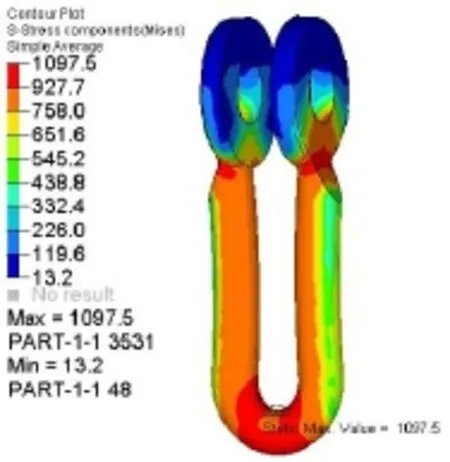
图13　面面接触下的应力云图

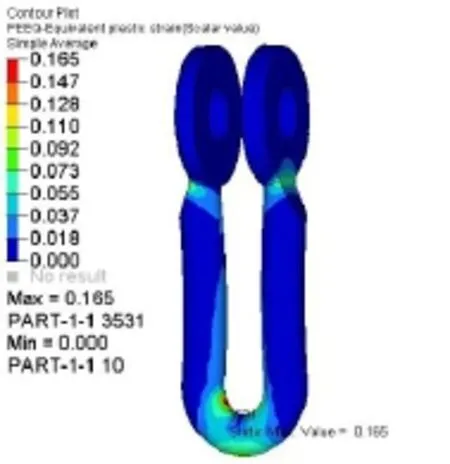
图14　面面接触下的塑性应变云图

4.3结果对比讨论

图8为载荷达到768 kN时，绑定接触计算的U型挂环变形图。U型挂环槽底变形最大，为14.6 mm。当材料发生塑性变形后，位移急剧增大，呈现明显的非线性特征(图 7)。图 12为载荷达到768 kN时，面面接触计算的U型挂环变形图。同样U型挂环槽底变形最大，变形量为6.4 mm。材料发生塑性变形后，位移呈明显的非线性特征(图11)。

图15为绑定接触和面面接触下U型挂环的位移-载荷曲线对比，通过对比图可看出，设置绑定与面面接触这2种不同的接触算法时，最大载荷下的变形量相差128.1%，存在较大差异。当载荷逐渐增大至768 kN时，U型挂环槽底局部区域已不再是圆弧形状而是呈直线(图16左)。而实际情况中，因U型挂环底部连接的同样为U型连接件，通常在一定的拉力载荷下，U型挂环槽底部不会出现此种变形，如出现是因为在仿真模拟时槽底与连接件之间设置绑定接触，导致载荷从小逐渐增大过程中两个接触的零部件间未出现相对滑移，U型挂环槽底被绑定的网格直接拉伸，两个U型臂呈现出明显的内凹，误差较大。

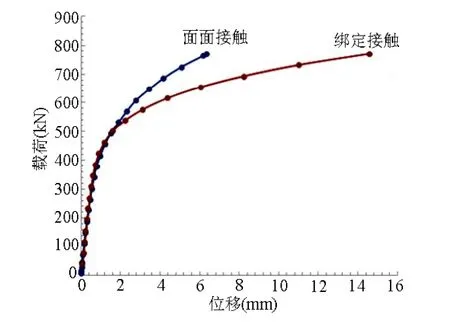
图15　绑定与面面接触位移-载荷曲线对比

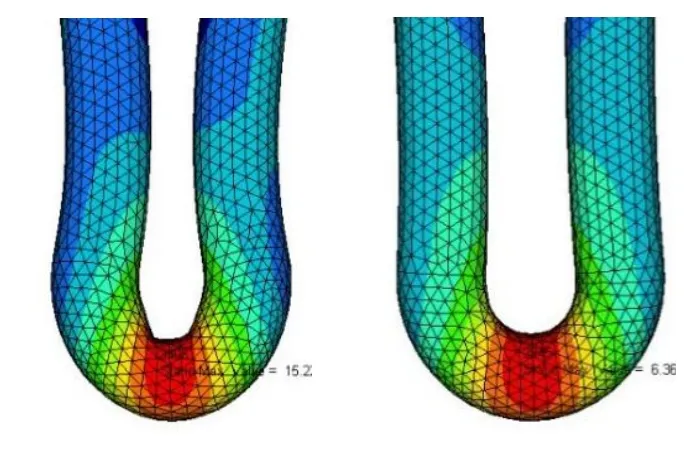
图16　绑定与面面接触变形对比

从图9和图13可看出，绑定接触与面面接触计算的U型挂环应力分布相接近，当载荷为768 kN时，绑定接触下的U型挂环最大应力达1 100 MPa，已达到材料的极限强度；面面接触下的U型挂环最大应力达1 097 MPa，接近材料的极限强度。

本文所研究的U型挂环承受拉力载荷，因载荷是从小到大缓慢施加，在载荷增大的过程中两个零部件首先需要消除间隙直至无相对位移，在消除间隙的过程中两个零部件的接触部位则会发生小的相对位移，而不是从始至终粘连在一起。如果将两个零部件的接触部位粘连在一起，就有可能导致变形量及等效塑性变形过大，误差不可接受。所以本文研究的U型挂环与连接件间需要设置面面接触，不建议为求模型简化与缩短计算时长而使用绑定接触。

从面面接触的计算结果可以看出，当载荷达到768 kN时，最大应力达1 097 MPa，接近材料的极限强度，同时U型挂环的塑性变形区域已贯穿挂环槽底，易发生破坏断裂，出于安全考虑，建议U型挂环选用强度更高的材料。此外，U型挂环颈部也出现了塑性区，此处为U型挂环截面变化区，在截面变化区域，特别是截面变化较剧烈的部位，应力往往得不到有效传递。建议将颈部设计做平滑处理，使截面缓慢过渡。

5　结 束 语

本文利用Abaqus软件，考虑材料非线性，将U型挂环与其连接件间接触类型分别设置为绑定接触和面面接触，并对这两种不同接触类型的计算结果作了对比分析。结果表明：

(1) 当采用绑定接触时，U型挂环槽底局部区域已不再是弧形结构而是呈直线，与实际不符；面面接触允许两个接触面间存在相对滑移，故U型挂环槽底变形较光滑，符合实际变形情况，故本文研究的U型挂环在给定工况下，应设置为面面接触。

(2) 从面面接触的计算结果可以看出，U型挂环的最大应力已接近极限强度，塑性变形区域贯穿U型挂环槽底，出于安全考虑，建议选用强度更高的材料。针对颈部截面变化区域的塑性变形，建议将颈部做平滑处理，使应力得到有效传递。

[1] 孙林松, 王德信, 谢能刚. 接触问题有限元分析方法综述[J]. 水利水电科技进展, 2001, 21(3): 18-20.

[2] 赵杰, 常俊英, 陈家庆. ANSYS在求解带摩擦接触问题中的应用[J]. 北京石油化工学院学报, 2003, 11(4): 45-48.

[3] 蔡猛昌. 基于有限元的新型碗头挂板分析与研究[D].扬州: 扬州大学, 2014.

[4] 庄卓, 由小川, 廖剑晖, 等. 基于ABAQUS的有限元分析和应用[M]. 北京: 清华大学出版社, 2009: 287-350.

[5] 石亦平, 周玉蓉. ABAQUS有限元实例分析详解[M].北京: 机械工业出版社, 2006: 126-133.

[6] 才博. 机械零部件设计中的非线性接触分析研究[D].乌鲁木齐: 新疆农业大学, 2005.

[7] 张建超, 王军, 刘涛, 等. 造桥机结构的有限元仿真分析[J]. 图学学报, 2013, 34(4): 98-104.

Contact Analysis of Link-Fitting with High-Strength Material Based on Abaqus

Li Junhui1,Xu Guanghui1,Chang Linjing1,Song Tiechuang1,Wan Shaoting2,Xu Aibin2

(1. Pinggao Group Co., Ltd., Pingdingshan Henan 467001, China; 2. Beijing Internet Based Engineering Co., Ltd., Beijing 100083, China)

Contact problem is a highly nonlinear behavior. Different contact types and control factors have an important effect on the results of the simulation model. In this study, the ability of resisting to deformation of link-fitting with high-strength material was simulated by FEA, using commercial software Abaqus. Different contact types between U-shackle and its connecting part were set up. Upon comparison and analyzation of the results with different contact types, it is clear that the contact type of U-shackle is suitable for the given service condition. Through nonlinear static analysis, the stress and deformation distributions of link-fitting were obtained. According to the results, modification suggestions were put forward, which provides a scientific guidance for the design of the link-fitting.

link-fitting; nonlinear; contact; finite element simulation

O 312.3

10.11996/JG.j.2095-302X.2016020184

A

2095-302X(2016)02-0184-05

2015-09-30；定稿日期：2015-11-13

国家电网公司科技项目(KY2014001)

李俊辉(1982–)，男，河南平顶山人，工程师，本科。主要研究方向为电力金具、仿真分析。E-mail：lijunhui2782@163.com