改进的最小包围球随机增量算法

李世林， 李红军

(北京林业大学理学院，北京 100083)

改进的最小包围球随机增量算法

李世林， 李红军

(北京林业大学理学院，北京 100083)

三维空间中离散点集的最小包围球，在碰撞检测、计算几何和模式识别等领域都有广泛应用。为了更好地理解和构造最小包围球算法，首先对最小包围球的性质进行分析。然后，基于对随机增量算法的分析，提出了构造较大初始包围球和减少迭代过程中最小包围球更新次数两种策略。依据后一种策略提出的方法称为随机点组-重算最远点算法。计算机随机生成数据和现实三维模型采样数据的多组实验结果表明，随机点组-重算最远点算法相比于之前的经典算法能够有效地提高时间效率。

最小包围球；随机增量算法；随机点组-重算最远点算法

对于三维空间中的离散点集P，求解其最小包围球(minimum enclosing ball，MEB)以寻找一个半径最小的球，其包含P中所有的点，球体有许多良好的性质[1]，因此在计算机图形学和计算几何中，与离散点集的凸包围多面体[2]相比，包围球常作为边界，可以更快地进行近似的碰撞检测、范围界定和形状分析。在空间数据库中，MEB的求解可用于建立空间数据索引，以便提高查询速度[3]。同时MEB问题在模式识别[4]、计算几何[5]、机器学习[6]等领域也有广泛应用。模型局部的包围球可以用于模型裁剪[7]或者重采样，因这些领域处理的数据集通常都是大规模的，所以提高MEB算法运行效率是很有必要的。

MEB问题可以追溯到19世纪中期，Sylvester[8]在1857年提出了最小包围圆问题，并在1860年，给出了求解该问题的一种近似线性算法[9]。之后人们开始系统地研究该问题，比如最近的基于α-壳的最小包围圆求解算法[10]，并研究从二维平面到三维空间再到更高维空间的算法；1982年，Megiddo[11]首次给出了一种理论上的线性时间算法，其时间复杂度是最小的，但算法本身的实现却很复杂；1991年，Welzl[12]提出了一种简单快捷的随机算法，其时间复杂度是线性级的，并指出该算法易于推广到高维空间的 MEB和最小包围椭球(minimum enclosing ellipsoid)中。后来，Berg等[5]对该方法进行了进一步的改进，称之为随机增量算法(randomized incremental algorithm，RIA)，该算法是求解MEB问题有代表性的经典算法。分析该算法可看出，影响求解的时间效率主要因素是MEB更新的次数，因此提高算法效率的策略有2种：①构造较大的初始 MEB；②修改迭代过程中的选点规则。在给出这两种策略对应的具体算法之前，为便于理解和构造算法，先概述MEB的性质。

1　离散点集的最小包围球及其性质

定义1. 点集P的MEB定义为：

其中， o*为最优球心，r*为最优半径，表示Euclidean范数。

2012年，文献[13]给出一系列有关最小包围圆的性质，这里对应给出三维空间中MEB的有关性质，这将有助于RIA的理解和实现。

性质1. 三维空间中，有限离散点集的MEB是唯一的。

此性质的证明见文献[12]。

若P中只有一个点p1，则MEB是退化的，半径为0，球心为点p1。

性质2. 非退化的MEB可以由2～4个边界点定义。

证明. 点集P的MEB的构成有3种情况：

(1) 点集 P中距离最远的两个点(p1,p2)作为边界点，p1,p2两点之间距离的一半作为球半径，两点连线段的中点作为球心。

(2) 点集P中任意3个点求其最小包围圆，其中最大的圆半径为r，圆心为o，确定该圆的那 3个点(p1,p2,p3)，若点集P中的任何一点与o之间的距离都小于r，则点集 P的 MEB的球心为o，半径为r，边界点是p1,p2,p3。

(3) 若有4个边界点，那么点集P的MEB为这4个点所构成的空间四面体的外接球。由空间几何的知识可知，空间四面体的包围球是唯一的，若边界点多于4个，那么边界点集中任意4个点所确定的MEB是等同的，都可以归纳为4个边界点。

性质3. 若点集P的MEB是由p1,p2,p3,p44个边界点确定，那么这4个点的MEB是其所构成的空间四面体的外接球。

引理1. 设点集P的子集的 MEB为Di：

(1) 若点pi+ 1∈ Di，则点集的 MEB为Di+1= Di；

(2) 若点pi+ 1∉ Di，则点pi+1必定是在点集 P′的MEB即Di+1的边界上。

引理1是RIA的递增思想，其证明可参考文献[5]。

证明. 由性质 3的条件可知，任意 3个点所确定的MEB都不包含第4个点。设p1,p2,p3所确定的MEB是球o，p4∉o，由引理1可知，点p4是在点集的MEB的边界上。同理p1,p2,p3也在其边界上，又因为四面体的外接球是唯一的，所以该4个点的MEB是这4个点所构成空间四面体的外接球 。

2　较大初始最小包围球的随机增量算法

Berg等[5]给出一种易于理解的RIA，该算法的思想与动态规划问题中动态维护最优解有相似之处。根据文献[5]中关于平面点集最小包围圆 RIA的描述，容易给出三维空间MEB的RIA。

RIA还有很大的改进空间，初始点对的选取直接影响到整个算法的迭代次数。传统RIA只是随机选取了两个点作为初始MEB的直径，尽管可以从平均意义上获得比较好的时间效率且能避免最差的情况，但是迭代次数却很大。本文采用较远两点构造较大初始 MEB，以便减少后续迭代过程中MEB的更新次数。

步骤1. 构造较大初始MEB。在点集P中任取点p1，找出距离p1最远的点pi，再找出距离pi最远的点pj，以点pi,pj的连线作为直径，构造初始MEB，记为D2。此时的初始MEB大小相对于RIA更接近最优的 MEB D的大小，迭代中重新构造MEB的次数会变得更少，所以理论上改进后的RIA效率比原始算法更高。

后续步骤采用经典RIA，迭代更新当前MEB。

步骤2. 设MEB D2的两个点分别为p1,p2, 令i=3转到步骤3。

步骤3. 检验点pi，如果pi在包围球Di-1中，那么MEB不变，即Di=Di-1；否则需根据性质3重新构造MEB Di。

步骤4. 令i=i+1，若i≤n，则转到步骤3，否则算法终止，输出Dn的半径和球心。

显然，步骤1的时间复杂度为O(n)，步骤2为O(1)，步骤 3与步骤 4构成循环，时间复杂度为O(n)，因此该方法确定初始点对的时间复杂度也是O(n)。由于新的改进算法在步骤1选取较大的包围球，所以步骤3中的MEB重新构造的次数会大大减少，因此新的算法能够有效地提高时间效率，称该算法为较大初始MEB的RIA，记为iRIA。

3　随机点组-重算最远点算法

通过修改RIA迭代过程中的选点规则，提出了一种新算法，称为随机点组-重算最远点算法(random point group - recalculation the farthest point，R-RCF)。

3.1算法介绍

步骤1. 将P中各点打乱成一个随机排列p1,p2,···,pn。

步骤2. 作前4个点p1, p2,p3,p4确定的MEB。根据性质2和性质3，球的边界可能通过这4个点(4点的外接球)；也可能只通过其中的3个点(3点的外接圆构成球的最大截圆)，但包含第4点；还可能只通过其中的两个点，后一种情况球边界上的两点一定是位于球的一条直径的两端。令i=5，转到步骤3。

步骤3. 考察点pi，如果该点位于球外部，转到步骤4。否则，令i=i+1，若i≤n，执行步骤3；若i＞n，执行步骤5。

步骤4. 根据引理1，在p1,p2,p3,p4中任意选择3个点，加上pi，构造包含这5个点的MEB，且半径是所有满足条件所构造的MEB中最小的，此时确定该MEB的4个点记为新的 p1,p2,p3,p4，令i=i+1，若i≤n，执行步骤3；若i＞n，执行步骤5。

步骤5. 在点集P中找出距离MEB的球心最远点F。若F点已在球内或球边界上，则该球即为所求的球，算法结束。否则，执行步骤6。

步骤6. 以F为边界点，在点集｛p1, p2, p3, p4｝中选择3个点和点F一起构造新的MEB，使得这5个点都在球内，且半径是所构造的MEB中最小的，此时选择的3个点和点F记作新的 p1, p2,p3,p4，转到步骤5。

R-RCF将求解MEB问题分为2部分进行：①动态更新最优解利用了RIA的核心思想，该算法的优点是每次迭代所需的计算量远远小于RIA，但缺点是每次更新最优解会遗漏少部分已经位于上一步的MEB内部的点。②重算遗漏部分则是利用了最远点依次选取算法的思想[14]，且相对于最远点依次选取算法，该部分迭代次数更少，同时又重算了动态更新中所遗漏的部分，弥补了动态更新最优解的缺点。本文称该算法为R-RCF。

3.2算法分析

3.2.1算法重算部分的必要性

由于R-RCF算法在步骤4动态更新最优解的过程中会遗漏少部分已经包含在球内部的点，所以该算法加入了步骤5和步骤6，对步骤4动态更新最优解的过程中所遗漏的区域进行重算。为了更形象地说明该问题，以二维平面最小包围圆为例进行分析。

如图1所示，ci是点ABC所确定的最小包围圆，当遍历到点D时，由于点D不在ci里，所以需要更新最小包围圆，ci+1是满足算法步骤 4的圆，此时s区域内遍历过的点已经不包含于更新后的最小包围圆中，要想使其重新位于最小包围圆中，就需要对该区域进行重算。该算法根据参考文献[14]中算法的步骤3，采用重算最远点的方法进行重算，同时该算法动态更新最优解的思想恰是参考RIA，且利用边界点动态更新最优解。

图1　R-RCF更新最优解时遗漏s区域的点

3.2.2算法收敛性

本节要证明上述 R-RCF算法一定能终止，且最后一次求得的MEB就是包含点集P中所有点的MEB。

引理2. 算法步骤4和步骤6所生成的MEB的半径是递增的。

证明. 设步骤4生成的包含A, B, C, D 4点的MEB为B1，半径为 r1；当考虑球外的点E后，生成的包含A, B, C, D, E 5点的MEB记为B2，半径为r2，显然B2包含A, B, C, D 4点。考虑到B2的构造，会有B2≠B1。若r1=r2，与空间离散点集的 MEB的唯一性存在矛盾；若r1＞r2，与点A, B, C, D的MEB为 B1也存在矛盾；所以r1＜r2，即更新后的MEB半径比原MEB的半径大。

定理1. 上述R-RCF算法是收敛的，且最后一次得到的MEB是包含点集P中所有点的MEB。

证明. 因为在点集P中任取4个点、3个点或2个点所生成的MEB的个数是有限的。由引理2可知，算法进行过程中所生成的MEB半径是递增的，经过有限次迭代后，可求得这些最小球中半径最大的一个。从算法步骤5可知，只有当点集P中所有点都在由4个点、3个点或2个点生成的MEB内部时，算法结束，因而最后得到的MEB会是包含点集P中所有点的MEB。

4　实验验证

上述算法的实验是在笔记本电脑上进行的，计算机配置是 Intel(R) Core(TM) i3-2310M CPU @ 2.10 GHz处理器和 6 GB内存，程序运行环境MATLAB R2012a。实验针对RIA，iRIA和R-RCF的时间效率进行对比，实验数据分为两类：计算机随机生成点集(简称为随机点集)和现实对象采集的三维点集(简称为采样点集)。

4.1实验比较

为了对比在不同规模下的数据求取MEB的时间效率，设计了10组点集，点数n分别是100，200，300，400，500，1 000，2 000，3 000，4 000，5 000，每组数据分别进行500次实验。随机点集的生成范围有2种，矩形域随机点集和球形域随机点集。

实验 1. 是矩形域随机点集，随机点按照均匀分布产生于一个单位正方体，如下式：

表 1是在矩形域上采样所得出的实验数据，Red1表示iRIA相对于RIA的时间压缩比，Red2表示R-RCF相对于RIA的时间压缩比。从表1可看出，本文提出的 iRIA算法在时间代价方面能压缩 8%以上，且随着点数的增加，时间效率的提升越来越高。而本文提出的 R-RCF算法在时间代价方面能压缩66%以上，这将大幅度地提高求解MEB的时间运行效率。MEB的实验效果如图2(a)所示。

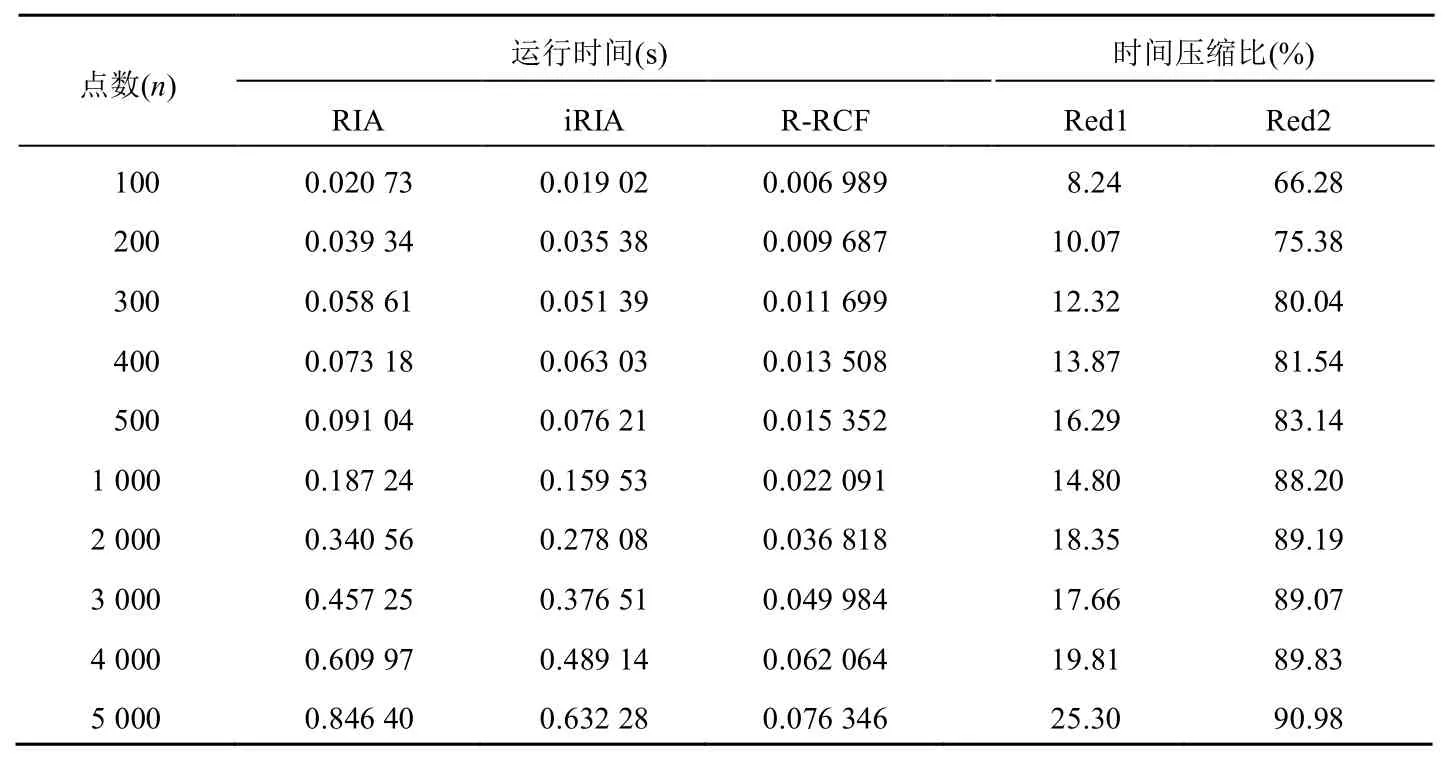
表1　矩形域上不同点数的平均运行时间比较

实验2. 针对球形域随机点集进行，随机点按照均匀分布产生于一个平移后的单位球。

球形域上MEB的求取效果如图2(b)所示。实验结果见表2。从时间效率上看，本文所提出的iRIA算法由于第一步计算较远的两个点增加了不少时间，同时，由于球形域点集形状对称的特点，本文改进后的 iRIA算法并不能有效地减少迭代次数，所以总时间代价上表现的略差些。但是本文提出的R-RCF算法在计算球形域点集的MEB在时间代价上能压缩71%以上。

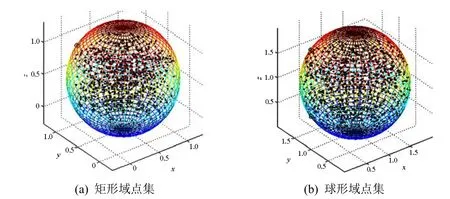
图2　离散点集最小包围球计算结果

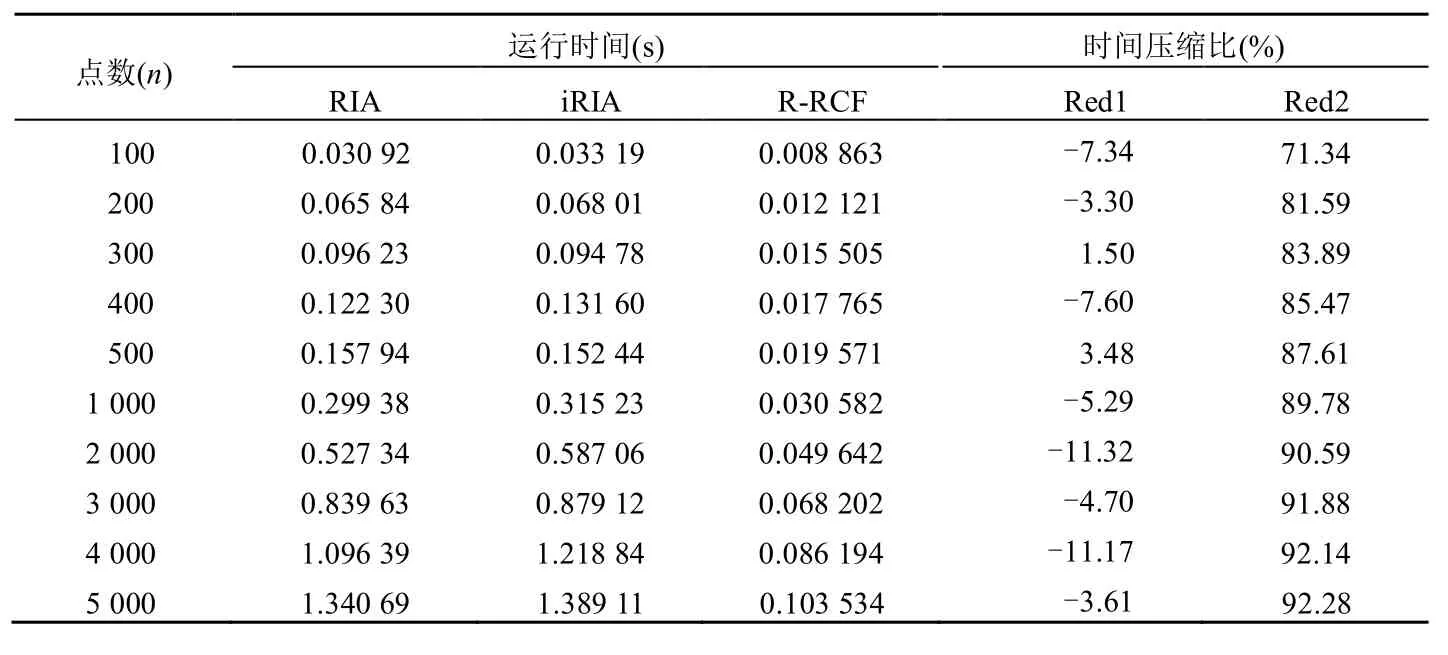
表2　球形域上不同点数的平均运行时间比较

在表2中，由于RIA和iRIA的运行时间相差并不大，故进行了方差未知均值相等(H0:μ1=μ2)的假设验证。当取显著性水平为0.05时，接受H0，即认为此两种算法针对球形区域的时间效率无显著差异。

4.2采样点集的最小包围球

在三维游戏制作或者三维激光测量中，需获得各种形状的点云数据。为了验证RIA、iRIA和R-RCF针对不同复杂数据的时间效率，将进行MEB计算，针对6个现实对象采集的三维点集，分别为网络公开数据库(http://visionair.ge.imati.cnr.it/ontologies/shapes/)人手、花瓶和佛像模型的采样点集，以及实验室扫描数据：树1、树2和场景模型，如图3所示。

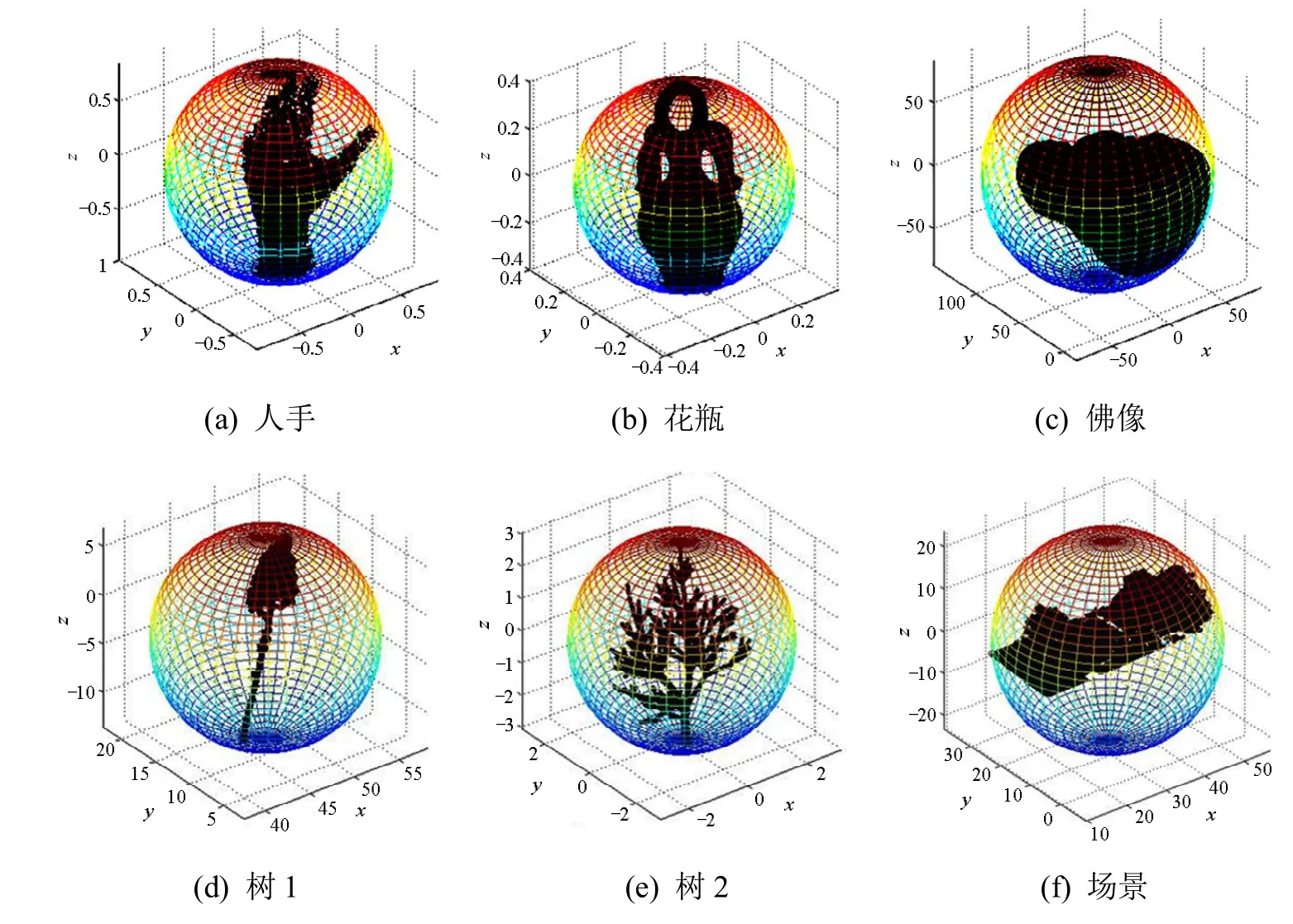
图3　现实三维模型采集数据的最小包围球

6组数据的点数和3种算法的时间及其效率比较见表3，其中运行时间是实验重复30次的平均运行时间。从表3看出，本文提出的改进算法iRIA的平均运行时间比RIA快10%～33%，R-RCF比RIA 快51%～93%。具体来说，iRIA与RIA之间的比较效果：对于比较“修长”的点集数据模型，如人手模型、树1模型和树2模型，iRIA的程序运行效率比RIA提高了22%以上，这是因为对于该类的点集数据模型，iRIA算法改进的初始值能大大减少求解MEB的迭代次数，这与矩形域随机点集得出的结论一致；而对于一些比较“饱满”的点集数据模型，如花瓶模型、佛像模型和场景模型，iRIA的程序运行效率比RIA提高的程度明显低于“修长”的点集数据模型，这与球形域随机点集得出的结论一致。从表3中的实验结果可以看出，针对不同形状的采样点集，iRIA算法的运行效率普遍高于RIA。R-RCF与RIA之间的比较效果：对于比较“饱满”的点集数据模型，R-RCF的程序运行效率比RIA提高了89%以上。可见，针对不同形状的大规模点集，本文提出的新算法R-RCF的运行效率远高于原始算法，同时，对于“饱满”的点集数据模型，效果尤其明显，这将为计算离散点集的MEB的工程应用节省大量的时间。

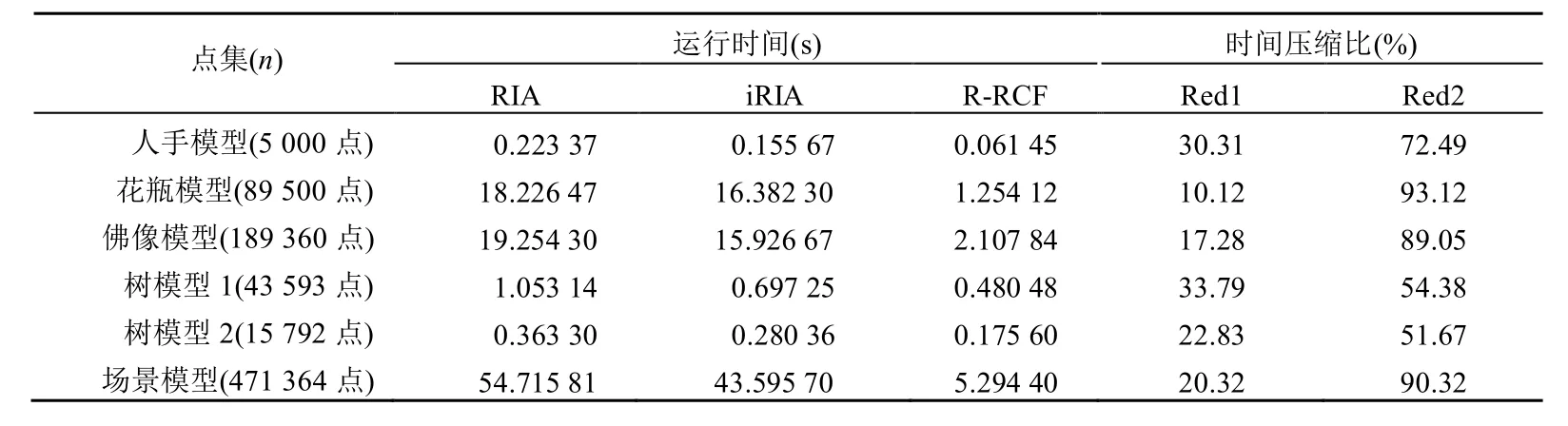
表3　3种算法针对激光扫描点云数据的平均运行时间比较

5　结 束 语

针对三维空间中求取离散点集MEB问题，为便于构造求解MEB的算法，本文先概述了三维空间中离散点集的MEB的几条主要性质。在分析求解MEB的RIA的基础上，提出一种称为较大初始MEB的 RIA，这种算法通过在第一阶段选取较远点对构造初始 MEB，有效地减少了第二阶段的MEB更新次数，提高了算法的时间效率。同时，本文又提出了一种新算法，称之为R-RCF，该算法通过减少迭代过程中MEB的更新次数，大幅度提高了时间效率。通过随机数据和现实三维模型采样数据等多组实验验证，结果表明，与原始RIA相比，本文提出的R-RCF算法能大幅度的提高时间效率。本文算法分析详细，有助于学生或者工程技术人员在算法实现过程中较好地处理相关细节。

此外，因为最小包络长方体比MEB更加接近物体表面，所以参考本文的研究思路和二维空间中最狭长包络矩形的求解原理及方法[15]，研究三维空间的最小包络长方体的快速计算是未来的一个研究方向。

[1] Hu P, Xu D, Li H. A normalization method of moment invariants for 3D objects on different manifolds [J]. Computer Aided Drafting, Design and Manufacturing, 2014, 24(2): 15-22.

[2] 唐磊, 施侃乐, 雍俊海, 等. 模型适应的凸包围多面体并行生成算法[J]. 中国科学: 信息科学, 2014, 44(12): 1515-1526.

[3] Samet H. The design and analysis of spatial data structures [M]. New Jersey: Addison Wesley Press, 1990: 86-89.

[4] 来疆亮, 王守觉. 最小球覆盖几何算法及其在模式识别中的应用[J]. 模式识别与人工智能, 2006, 19(2): 271-276.

[5] Berg M D, Jreveld M V. Overmars M, et al. 计算几何:算法与应用[M]. 邓俊辉, 译. 北京: 清华大学出版社, 2005: 99-103.

[6] Ben-Hur A, Horn D, Siegelmann H T, et al. Support vector clustering [J]. Journal of Machine Learning Research, 2001, 2(2): 125-137.

[7] 耿博, 张慧娟, 王衡, 等. 离散曲面的近似 Poisson盘采样[J]. 中国科学: 信息科学, 2012, 42(6): 703-716.

[8] Sylvester J J. A question on the geometry of situation [J]. The Quarterly Journal of Pure and Applied Mathematics, 1857, (1): 79.

[9] Sylvester J J. On Poncelet’s approximate linear valuation of surd forms [J]. Philosophical Magazine, 1860, 20(132): 203-222.

[10] 张勇, 陈强. 一种基于计算几何方法的最小包容圆求解算法[J]. 工程图学学报, 2007, 28(3): 97-101.

[11] Megiddo N. Linear-time algorithms for linear programming in R3 and related problems [J]. Siam Journal of Computing. IEEE, 1983, 12(4): 329-338.

[12] Welzl E. Smallest enclosing disks (balls and ellipsoids) [J]. Lecture Notes in Computer Science, 1991, 555(1): 359-370.

[13] 李红军, 张晓鹏. 离散点集最小包围圆算法分析与改进[J].图学学报, 2012, 33(2): 34-38.

[14] 汪卫, 王文平, 汪嘉业. 求一个包含点集所有点的最小圆的算法[J]. 软件学报, 2000, 11(9): 1237-1240.

[15] 周敏, 郑国磊, 陈树林. 二维图形最狭长包络矩形的求解原理及方法[J]. 图学学报, 2013, 34(4): 46-53.

An Im proved Random ized Incremental A lgorithm for Generating M inimum Enclosing Ball of Discrete Point Set

Li Shilin,Li Hongjun

(College of Science, Beijing Forestry University, Beijing 100083, China)

The minimum enclosing ball (MEB) of discrete point set in the 3D space has been w idely used in many fields, such as collision detection, computational geometry, pattern recognition and so on. In order to better understand and construct MEB, its character is analyzed firstly. A fter analyzing the classical randomized incremental algorithm, we propose two strategies to improve time efficiency. One strategy is to construct a bigger initial enclosing ball and another strategy is to decrease the number of updating MEB. Based on the second strategy, a new algorithm called random point group-recalculation farthest point is proposed. Multi-group experimental results, whose data are both random ly generated by computer and realistic 3D model sampling, show that the random point group-recalculation farthest point algorithm can effectively improve the time efficiency compared with the classical algorithms.

minimum enclosing ball; randomized incremental algorithm; random point grouprecalculation farthest point

TP 391

10.11996/JG.j.2095-302X.2016020166

A

2095-302X(2016)02-0166-06

2015-09-24；定稿日期：2015-10-03

国家自然科学基金项目(61372190)

李世林(1992–)，男，山东青岛人，硕士研究生。主要研究方向为计算几何。E-mail：lishilin_2015@bjfu.edu.cn

李红军(1969–)，男，湖南郴州人，副教授，博士。主要研究方向为计算机图形学和计算几何等。E-mail：lihongjun69@bjfu.edu.cn