六次PH曲线G2Hermite插值

王　慧， 朱春钢， 李彩云

(1. 大连理工大学数学科学学院，辽宁 大连 116024；2. 大连理工大学盘锦校区基础教学部，辽宁 盘锦 124221)

六次PH曲线G2Hermite插值

王慧1， 朱春钢1， 李彩云2

(1. 大连理工大学数学科学学院，辽宁 大连 116024；2. 大连理工大学盘锦校区基础教学部，辽宁 盘锦 124221)

以其在弧长计算与等距线表示上的优势，PH曲线成为近年来计算机辅助几何设计研究的焦点问题之一。为此讨论了六次PH曲线的G2Hermite插值问题。在指定自由参数下，对两类六次PH曲线分别进行复分析曲线求解，得到满足G2插值条件的六次PH曲线和控制顶点。通过弧长、能量积分、绝对旋转数的衡量，选取较好的插值曲线。进一步，讨论了用六次PH曲线G2Herm ite插值逼近90°和67°圆弧的问题。在同一个自由参数下，选择插值最好的曲线，可实现六次C1Hermite插值逼近圆弧的效果，且逼近90°圆弧时，优于五次G2Hermite插值逼近的PH曲线，而逼近67°圆弧时，与最好的五次PH曲线达到的效果几乎相同。

PH曲线；G2Herm ite插值；圆弧

1990年，Farouki和Sakkalis[1-2]提出一种速端曲线模长为多项式参数曲线的 (Pythagorean hodographs, PH)曲线。这种曲线克服了一般参数曲线的一些缺点，具有良好的性质，如弧长是原参数的多项式函数、等距线可以用精确的有理形式表示等，这些优点为数控加工和路径规划提供了方便。由于在几何与工业设计上的广泛应用，导致PH曲线的理论分析和应用性研究成为近些年来计算机辅助几何设计(computer aided geometric design, CAGD)研究的焦点之一，其中PH曲线插值是一个重要研究内容。

PH曲线插值一般分为Hermite插值和样条插值2种形式。在Hermite插值的研究中，可分为参数连续(Ci, i阶)和几何连续(Gj, j阶)Herm ite插值。Meek 和W alton[3]研究了一般的三次参数曲线的G1Hermite插值。1995年，Farouki和Neff[4]利用复分析的方法求解五次PH曲线的C1Hermite插值，在产生的4条满足Hermite条件的曲线中，利用计算旋转数来选择最优解。文献[5]采用速度参数化的方法用凸五次PH曲线求解C1Hermite插值问题。C1Hermite插值需用五次PH曲线解决文献[4]，C2Hermite插值需用九次PH曲线有效解决文献[6]，一般地，CkHermite插值可以用4k+1次PH曲线解决文献[7]。五次及五次以上PH曲线可以解决G2Herm ite问题，所以Jüttler[8]采用了七次PH曲线解决介C1和C2的G2Hermite插值问题。2002年，Walton和Meek[9]对G2Hermite插值问题分别构造了“C”和“S”形状的五次过渡PH曲线。陈国栋和王国瑾[10]用复形式表示，研究了五次PH曲线的G2Hermite插值求解。杨平和汪国昭[11-12]用同伦算法研究了C3连续的七次PH样条曲线和闭曲线插值问题。文献[13]用一种三次PH曲线逼近代数曲线，且逼近曲线具有G1连续性。文献[14-15]介绍了三次、五次、七次PH曲线控制多边形几何性质，文献[16-17]介绍了四次PH曲线控制多边形的特点。2015年，Farouki等[18]给出了两种判别三次和五次PH曲线的方法。由于PH曲线具有良好的几何性质，近年来，采用PH曲线对圆弧进行逼近也成为研究的热点问题。张伟红等[19]对圆弧进行了C1五次PH曲线等弧长逼近。2014年，Farouki[20]在G2Hermite插值条件下，利用具有单峰曲率特点的五次和能微调曲率的七次PH曲线构造了圆直角。

从以上研究发现，绝大多数都是基于奇次PH曲线的研究，主要原因是偶次PH曲线是非正则曲线会存在奇异点。方林聪和汪国昭[21]首次研究了六次PH曲线的C1Hermite插值问题，并将曲线分成两类讨论，通过自由参数的控制，构造了六次PH曲线。在实际应用中，有对已知型值点采用两端点的位矢、单位切矢和有向曲率构造Hermite插值的需要，在现有的G2Hermite插值和六次PH曲线的分析理论上，本文研究了六次PH曲线的G2Hermite插值问题。并从复分析的角度，对自由参数进行选取，避免了六次PH曲线出现奇异点的情况，从而构造了两类情况下六条不同的六次PH曲线。利用弧长、能量积分、绝对旋转数等度量标准，选择较好的插值曲线。对比满足G2Hermite插值条件的六次PH曲线插值逼近圆弧的6个结果，得到最好的两条六次PH曲线。同时对比五次PH曲线G2Hermite插值逼近圆弧和六次PH曲线C1Hermite插值逼近圆弧的研究发现，90°圆弧的六次PH曲线里，式(18)的G2Hermite插值逼近效果最好，对于67°圆弧，最好的六次、五次G2Hermite插值以及六次C1Hermite插值PH曲线的逼近效果几乎相同。

1　六次PH曲线

1990年，Farouki和Sakkalis[1]定义了PH曲线并给出其相关性质。Farouki[2]在2008年又从代数与几何的角度，总结了之前对平面PH曲线和空间PH曲线的研究工作。有关PH曲线的定义和相关定理介绍如下(其中黑斜体字母表示复变量)：

定义1[1]. 平面多项式参数曲线r(t)=(x(t), y(t))称为 PH曲线，如果存在多项式σ(t)，使得x′2(t)+y′2(t)=σ2(t )。

一条平面参数曲线 r (t)=(x(t), y(t))的复表示为r(t)=x(t)+iy(t)。

定理 1[1]. 平面参数曲线r(t)=x( t)+iy( t )是PH曲线的充要条件，其为：

其中，w( t), u( t), v( t)为非零实系数多项式，u(t)与v(t)不同时为常数。

由定理1可以得到如下等价定理：

定理 2[2]. 平面参数曲线 r (t)=(x( t), y(t))是PH曲线的充要条件，为r(t)的速端曲线：

其中，Q(t)=u( t)+iv( t)。

设平面n次Bézier曲线r(t)的控制顶点记为Pj, j=0,…,n，控制顶点的一阶向前差分为ΔPj=Pj+1-Pj，则n次Bézier曲线的速端曲线r′(t)可以表示为：

定理3[2]. 平面n次Bézier曲线r(t)是PH曲线的充要条件，为r(t)的速端曲线：

其中，w(t)为实系数多项式，Q(t)为复系数多项式。

其中，实系数多项式w(t)和复系数多项式Q(t)也表示为Bézier形式。

引理4[2]. n次PH曲线r(t)=x(t)+iy(t)满足的次数关系是n= n1+2n2+1，其中n1=deg(w), n2=max[deg(u), deg(v)]。

当n=6时, n1,n2取值有2种情况：n1=3,n2=1 或n1=1,n2=2，对应的2类曲线分别为：

其中，wi( i=0,1,2)为待定实系数，uj( j=0,1)为待定复系数。

其中，w0为待定实系数，ui( i=0,1,2)为待定复系数。

易知，r′(t)的奇异点与实多项式w(t)的根对应。由代数基本定理可知，第一类六次PH曲线上可能存在3个奇异点，第二类六次PH曲线存在一个奇异点，使其为非正则曲线。

2　六次PH曲线的G2 Hermite插值

定义 2[6]. 六次 PH 曲线, t∈[0,1]，若满足：

2.1第一类曲线

将向量进行复形式表示，记：

若给定式(*)和w0，将式(6)、(7)联立，可以求得λ,μ值。将其代入式(4)、(5)求出 u0,u1，再由式(3)，分离实部和虚部，解关于w1, w2的二元一次方程组，从而最终求得六次PH曲线及其控制顶点。

虽然式(4)、(5)的符号选择有4种组合情况，但是式(6)、(7)所得表达结果唯一，其求解出来的是两组互为相反数的(λ,μ)，分别代回式(3)，得到的两组w1, w2相同，因此求得第一种六次PH曲线只有一条。

设ξi,( i=1,2,3)为实多项式w(t)的3个代数根，则。w0＞0说明(0,1)区间存在两个奇异点或者不存在奇异点，而w0＜0说明(0,1)区间存在1个或3个奇异点[20]。因此，自由参数w0可以体现出六次PH曲线奇异点情况。

例1. 取与文献[10]相同的插值条件：P0=-5, P6=6,T0=0.5154+0.8575i,T1=0.4472-0.8944i, k0=-0.11, k1=-0.14。

令w0=1，代入上述分析过程，得到关于w1,w2的方程组：

进而可计算得到满足G2Hermite插值条件(*)的六次PH曲线为如图1(a)所示：

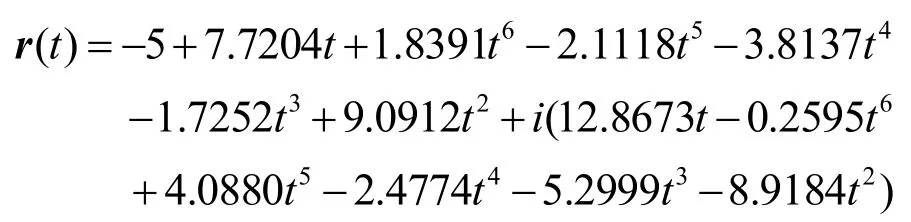
其控制顶点为：

令w0=0.5，关于1,2ww的方程组为：

计算可得满足G2Hermite插值条件(*)的六次PH曲线，如图1(b)所示：

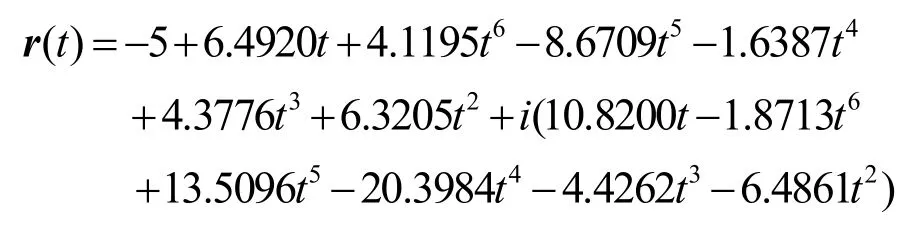
其控制顶点为：

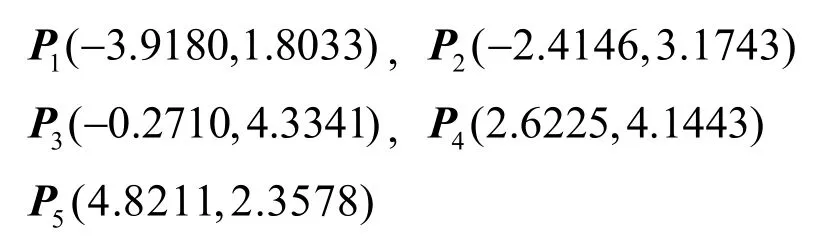
令w0=0.1, 关于1,2w w的方程组为：

计算可得满足G2Hermite插值条件(*)的六次PH曲线，如图1(c)所示：

其控制顶点为：

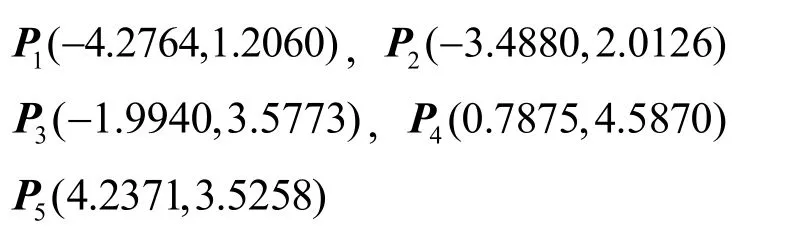
图1　第一类六次PH曲线w0取不同值时的图像

对于以上3种不同w0的取值情况，采用如下选取标准对曲线度量[2]：

其中，k为曲率。

以上3类积分，采用105为细分单位求其数值解。并对以下选取标准的求解施以相同方法。

从表1可知，w0=0.5时其弧长小于w0=1且大于w0=0.1，但其能量积分、绝对旋转数都是三者中最小的。

表1　第一类六次PH曲线w0取不同值时的选取标准

2.2第二类曲线

(2)创建宗地的关联属性方法。如在调查库中查看宗地属性时，发现没有相应的属性信息，系统可自动获取宗地上的建筑面积、容积率等关联信息，即创建关联属性的方式来获取相应的属性。

若给定式(*)和w0，将式(15)、(16)联立，可以用(λ,μ)表示出u1,x，u1,y，再将式(12)、(13)代入式(11)，分离实部和虚部得到关于(λ,μ)的二元六次方程组，将求出的(λ, μ)代回式(12)～(14)求得u0, u1, u2，进而得到原六次PH曲线和控制顶点。

式(12)、(13)符号有(+,+),(+,-),(-,+),(-,-) 4种组合情况，符号的差异会得到不同的(λ, μ)值。通过以下几组实例数据发现，给定 w0值，每组符号均得到10组互为相反数的不同(λ, μ)值，且4组符号得到对应的(λ, μ)绝对值相同。类似上一种，互为相反数的(λ, μ)求得的PH曲线也一样，所以每种符号求得5条不同的曲线。而式(12)符号的改变，会导致μ值符号改变，同样式(13)符号的改变，也决定λ值符号的改变，但最终得到的控制顶点坐标和六次 PH曲线是一致的，说明绝对值相同的(λ, μ)求得的PH曲线也一样，所以最终只有5条不同的第二种六次PH曲线，如图2～3所示。

例2. 取与例1相同的G2Herm ite插值条件。w0= 1，w0=0.5，w0=0.1时，相应的关于(λ, μ)的二元六次方程组如下，六次PH曲线及其控制顶点如图2～4所示。

如表2并结合图形，比较以上标准可发现，13条六次PH曲线的弧长相近；有尖点出现的曲线弧长相对较长，能量积分和绝对旋转数偏大；能量积分越小，绝对旋转数也越小。综合来看，图2(a～c)、图3(a～c)、图4(a)均较好地满足了G2Hermite插值条件的PH曲线。

图2　第二类六次PH曲线w0=1时的图像

图3　第二类六次PH曲线w0=0.5时的图像

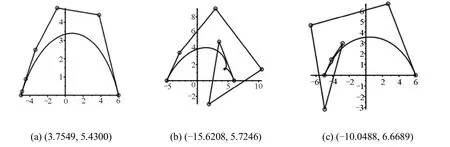
图4　第二类六次PH曲线w0=0.1时的图像

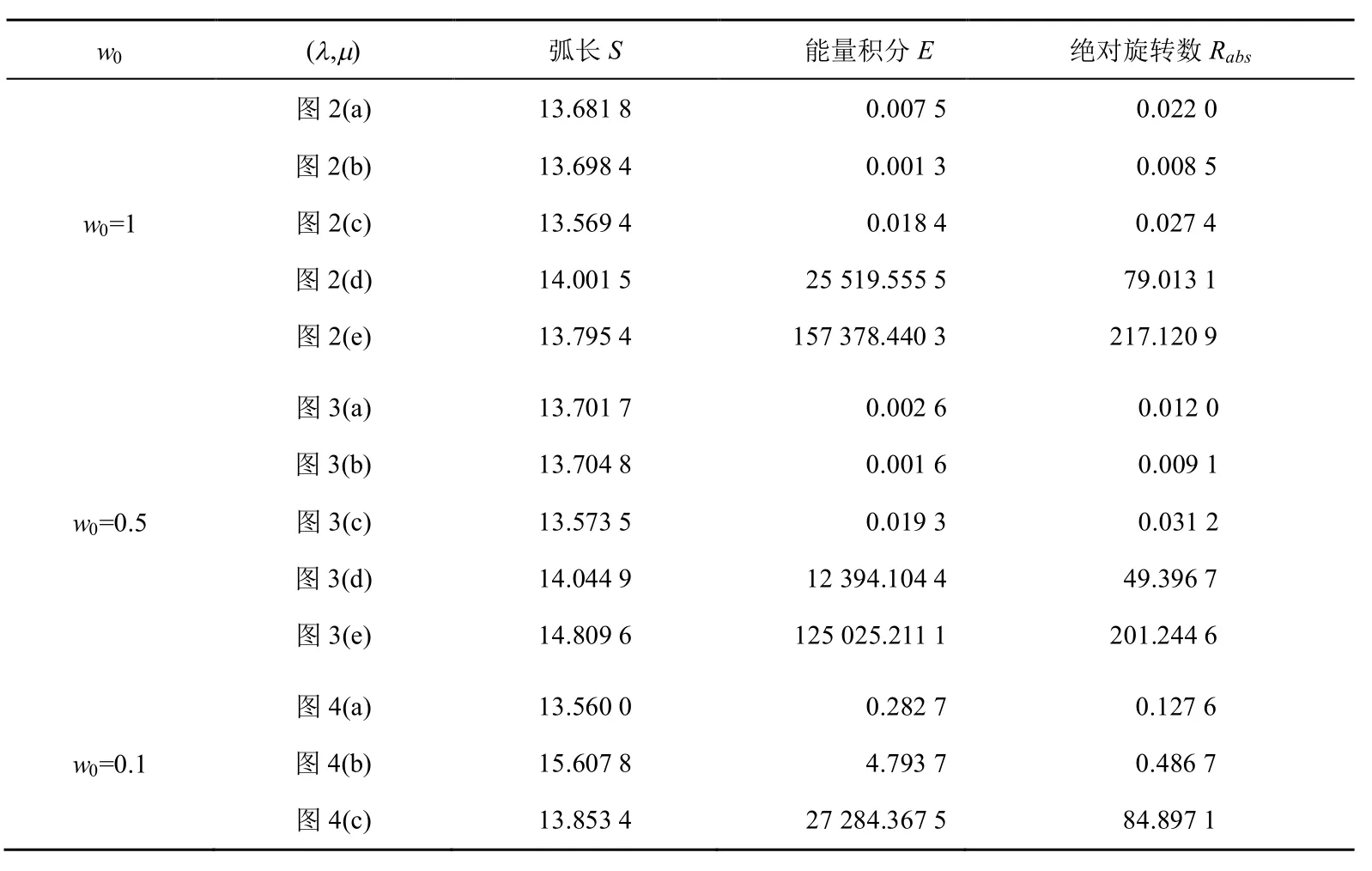
表 2　第二类六次PH曲线w0取不同值时的选取标准

本文不研究 w0对曲线的决定作用，所以针对例1和例2的G2Hermite插值条件，只给出了w0分别取 1，0.5，0.1时对应的曲线和衡量标准。第一类曲线里，w0=0.5是较好的曲线，其弧长介于两者之间，能量积分和绝对旋转数均最小。第二类曲线里，w0=1和 w0=0.5的满足条件且较好的曲线数量要多于w0=0.1，且w0=1和w0=0.5的衡量标准相近。下面采用的是w0=0.5的六次PH曲线解决插值逼近圆弧的问题。一段圆弧，其满足的G2Hermite插值条件复表示为：

3　圆弧的六次PH曲线逼近

上面讨论了六次PH曲线的G2Hermite插值，下面利用以上分析解决插值逼近特殊的 90°和 67°圆弧的问题。其他度数的圆弧，可以类似得到，也可以利用对称等变换或样条等知识解决更一般的圆弧插值逼近问题。这里w0=0.5。

3.190°圆弧的六次PH曲线逼近

弧长误差分别为0.000 424 5和0.000 082 68。

采用六次PH曲线逼近x2+(y-1)2=1的四分之

图5　90°圆弧的G2六次PH插值曲线

表 3　90°圆弧的G2六次PH曲线选取标准

为了检验六次PH曲线G2Hermite插值逼近圆弧的效果，将其与圆弧的五次PH曲线G2Herm ite插值逼近和圆弧的六次PH曲线C1Hermite插值逼近进行对比。

(1) 90°圆弧的五次PH曲线G2Hermite插值逼近。依据文献[10]的方法，在G2Hermite插值条件(**)下，得到满足条件的五次PH曲线本质上(将曲线及其控制顶点关于直线 y=-x+1对称的两条曲线算作一条)有3条，如图6所示。选取标准见表4，其中弧长误差最小的是0.000 114 ，对应的是五次PH曲线 G2Herm ite插值逼近效果最好的曲线如图6(c)所示，但是和图5(d)的六次PH曲线比较见表3，曲线式(18)的插值逼近效果更好。

图6　90°圆弧的G2五次PH插值曲线

表 4　90°圆弧的G2五次PH插值曲线选取标准

(2) 90°圆弧的六次PH曲线C1Hermite插值逼近。依据文献[20]中的讨论，取 w0=0.5，若进行六次PH曲线C1Hermite插值逼近圆弧，需要构造C1Hermite插值条件：

为了和圆弧的六次PH曲线G2Hermite插值逼近进行比较，式(***)应分别选取第一类曲线式(17)的4个控制顶点P0=0,P1=0.1982, P5=1+0.7198i,P6=1+i和第二类曲线式(18)的4个控制顶点 P0=0,P1=0.2406,P5=1+0.7198i, P6=1+i。

第一类得到圆弧的 C1插值逼近六次 PH曲线(如图7(a)所示)的选取标准见表5与表3中第一类的相同，说明该六次 PH曲线与曲线(17)的插值逼近效果相同。第二类关于u1的一元二次复方程有2组解：u1= 1.3840+0.6133i ，u1=-5.1777- 2.1413i ，则求得圆弧的C1插值逼近六次PH曲线有两条，见图7(b)、(c)。显然图7(b)是较好的圆弧插值逼近曲线，且相应的选取标准(见表5)与曲线式(18)几乎相同，说明二者是插值逼近效果非常相近的曲线。

图7　90°圆弧的C1六次PH插值曲线

表 5　90°圆弧的C1六次PH插值曲线选取标准

以上结果分析，关于90°圆弧的Hermite插值逼近曲线，五次G2Hermite插值PH曲线的最好逼近效果，不如六次G2Hermite插值PH曲线的最好逼近效果。而2条六次G2Hermite插值PH曲线(17)、(18)的逼近效果与最好的2条六次C1Hermite插值PH曲线的逼近效果几乎相同。

3.267°圆弧的六次PH曲线逼近

采用六次PH曲线逼近x2+y2=1的67°圆弧，其满足的G2Hermite插值条件复表示为：

从得到的六次PH曲线(如图8所示)和选取标准(见表6)可知，图8(a)、(c)是近似效果最好的2条曲线，弧长误差分别为0.000 005 073和0.000 060 83。类似上述90°圆弧的分析，可以做这2条曲线确定的C1Hermite插值条件下的六次PH逼近曲线和式(****)条件下的五次PH逼近曲线，见图9与表7、图10与表8。

图8　67°圆弧的G2六次PH插值曲线

表6　67°圆弧的G2六次PH插值曲线选取标准

图9　67°圆弧的G2五次PH插值曲线

表 7　67°圆弧的G2五次PH插值曲线选取标准

图10　67°圆弧的C1六次PH插值曲线

表8　67°圆弧的C1六次PH插值曲线选取标准

从以上图形和表格数据发现，67°圆弧的逼近曲线里，最好的2条六次G2Hermite插值PH曲线的逼近效果与六次C1Hermite插值PH曲线的逼近效果几乎相同；但和 90°圆弧的逼近效果略有不同的是，最好的G2五次PH曲线和G2六次PH曲线的弧长误差有相同的数量级10-6，且前者的逼近效果略好于后者。

4　结　论

本文对六次PH曲线的G2Hermite插值进行了研究，对其依据次数关系分成两类，通过自由参数的确定，分别讨论了两类曲线在G2Herm ite插值条件下的曲线求解。对比曲线弧长、能量积分、绝对旋转数，选取了较好的插值曲线。其中自由参数恰恰是六次PH速端曲线r′(t)= w( t)Q2(t)中w(t)的一个系数 w0，其可以由r(t)的奇异点表示，因此控制了w0，便确定了六次PH曲线上奇异点的位置，从而简化了非正则的六次PH曲线的研究。对于第一类曲线，奇异点在曲线中的位置不易控制，但是第二类的更易控制，且表达结果更加丰富。依据以上分析，本文利用六次 PH曲线在 G2Hermite插值条件下，分别对90°和67°两种圆弧进行了逼近。对于每种圆弧逼近问题，取定一个自由参数，两类六次PH曲线都达到了很好的逼近效果，对比图像、弧长、弧长误差、能量积分、绝对旋转数，找到逼近效果最好的曲线。同时对五次PH曲线G2和六次PH曲线C1插值逼近这两种圆弧的研究发现，90°圆弧的逼近曲线里，式(18)的逼近效果最好，弧长误差为0.000 082 68。在式(17)、(18)确定的C1Hermite插值条件下，得到的逼近效果最好的两条C1六次PH曲线与式(17)、(18)近乎相同，说明C1六次PH曲线插值逼近90°圆弧的问题可以通过G2Hermite六次PH曲线求解，这个结论也体现在插值逼近67°圆弧上。在 67°圆弧的逼近曲线里，最好的五次和六次G2Hermite插值PH曲线逼近效果相近，弧长误差都达到10-6数量级。对圆弧的六次PH曲线逼近的研究突破了以往都是对奇次 PH曲线插值逼近圆弧的传统，在CAD和工业设计上，若提供了插值端点、切向量和曲率数据，可以利用六次PH曲线进行插值逼近，同时自由参数增加了构造的灵活性。

[1] Farouki R T, Sakkalis T. Pythagorean hodographs [J]. IBM Journal of Research and Development, 1990, 34(5): 736-752.

[2] Farouki R T. Pythagorean-hodographs curves: algebra and geometry inseparable [M]. Berlin: Springer Press, 2008: 369-377, 546-566.

[3] Meek D S, Walton D J. Geometric Hermite interpolation with Tschirnhausen cubics [J]. Journal of Computational and Applied Mathematics, 1997, 81: 299-309.

[4] Farouki R T, Neff C A. Hermite interpolation by Pythagorean hodograph quintics [J]. Mathematics of Computation, 1995, 64(212): 1589-1609.

[5] Kong J H, Jeong S P, Lee S, et al. C1Hermite interpolation with simple planar PH curves by speed reparametrization [J]. Computer Aided Geometric Design, 2008, 25(4): 214-229.

[6] Farouki R T, Manjunathaiah J, Jee S. Design of rational cam profiles with Pythagorean-hodograph curves [J]. Mechanism and Machine Theory, 1998, 33(6): 669-682.

[7] Sir Z, Jüttler B. Constructing acceleration continuous tool paths using Pythagorean hodograph curves [J]. Mechanism and Machine Theory, 2005, 40(11): 1258-1272.

[8] Jüttler B.Hermite interpolation by Pythagorean hodograph curves of degree seven [J]. Mathematics of Computation, 2001, 70(235): 1089-1111.

[9] Walton D J, Meek D S. Planar G2transition with a fair Pythagorean hodograph quintic curve [J]. Journal of Computational and Applied Mathematics, 2002, 138(1): 109-126.

[10] 陈国栋, 王国瑾. 五次PH曲线的 Hermite 插值[J]. 软件学报, 2001, 12(10): 1569-1572.

[11] 杨平, 汪国昭. C3连续的7次PH样条曲线插值[J].计算机辅助设计与图形学学报, 2014, 26(5): 731-738.

[12] 杨平, 汪国昭. C3连续的七次PH样条闭曲线插值[J].浙江大学学报: 工学版, 2014, 48(5): 934-941.

[13] 寿华好, 江瑜, 缪永伟. 基于三次PH曲线误差可控代数曲线等距线逼近算法[J]. 图学学报, 2012, 33(2): 30-33.

[14] Farouki R T. The conformal map2z→zof the hodograph plane [J]. Computer Aided Geometric Design, 1994, 11(4): 363-390.

[15] 杨平, 汪国昭. 7次PH曲线的控制多边形的几何性质[J]. 计算机辅助设计与图形学学报, 2014, 26(3): 378-384.

[16] Wang G Z, Fang L C. On control polygons of quartic Pythagorean-hodograph curves [J]. Computer Aided Geometric Design, 2009, 26(9): 1006-1015.

[17] Li Z, Ait-Haddou R, Biard L. Pythagorean hodograph spline spirals that match G3Hermite data from circles [J]. Journal of Computational and Applied Mathematics, 2015, 278: 162-180.

[18] Farouki R T, Giannelli C, Sestini A. Identification and “reverse engineering” of Pythagorean-hodograph curves [J]. Computer Aided Geometric Design, 2015, 34: 21-36.

[19] 张伟红, 蔡亦青, 冯玉瑜. 圆弧的五次PH曲线等弧长逼近[J]. 计算机辅助设计与图形学学报, 2010, 22(7): 1082-1086.

[20] Farouki R T.Construction of G2rounded corners with Pythagorean-hodograph curves [J]. Computer Aided Geometric Design, 2014, 31(2): 127-139.

[21] 方林聪, 汪国昭. 六次PH曲线C1Hermite插值[J]. 中国科学数学, 2014, 44(7): 799-804.

G2Herm ite Interpolation by Pythagorean Hodograph of Degree Six

Wang Hui1,Zhu Chungang1,Li Caiyun2

(1. School of Mathematical Sciences, Dalian University of Technology, Dalian Liaoning 116024, China; 2. School of Science, Dalian University of Technology, Panjin Liaoning 124221, China)

By the advantages of computing arcs and representing offsets, study of phythagorean hodograph curves is one of the hot topics in recent years. In this paper, G2Hermite interpolation by sextic PH curves is studied. Sextic PH curves can be classified into two types and the interpolation problem can be resolved to get the control points with some free parameter in complex representation. With the analysis of arc-length, bending energy and absolute rotation number, the better interpolation curves are selected. Moreover, the sextic PH G2Hermite interpolation is applied to approximate the 90° and 67° arcs. The best approximating curves can solve C1Hermite interpolation by the PH sextics. And the best curves’ performance is better than the quintic G2Hermite interpolation curves when approximating the 90° arc, and is almost same as the latter’s best curve when approximating the 67° arc.

PH curve; G2Hermite interpolation; arc

TP 391

10.11996/JG.j.2095-302X.2016020155

A

2095-302X(2016)02-0155-11

2015-09-24；定稿日期：2015-10-09

国家自然科学基金项目(11271060，11290143，11401077)；民用飞机专项项目(M J-F-2012-04)；中央基本科研业务费资助项目(DUT16LK38)；辽宁省高等学校优秀人才支持计划项目(LJQ2014010)

王慧(1990–)，女，吉林吉林人，博士研究生。主要研究方向为计算几何。E-mail：wanghui21301062@mail.dlut.edu.cn

朱春钢(1977–)，男，北京人，教授，博士，博士生导师。主要研究方向为计算几何。E-mail：cgzhu@dlut.edu.cn