非自治Kuramoto-Sivashinsky方程一致吸引子的存在性、一致有界性和收敛性

2016-11-29沈晓鹰马巧珍

华中师范大学学报（自然科学版） 2016年2期

关键词：对式内积西北师范大学

沈晓鹰, 马巧珍

(西北师范大学数学与统计学院, 兰州 730070)

非自治Kuramoto-Sivashinsky方程一致吸引子的存在性、一致有界性和收敛性

沈晓鹰, 马巧珍*

(西北师范大学数学与统计学院, 兰州 730070)

讨论了具有奇异振动外力项的Kuramoto-Sivashinsky方程

ut+Δ2u+Δu+u·u=g(x,t)+ε-ρh(t/ε),u|t=τ=uτ

和相应的Kuramoto-Sivashinsky方程

ut+Δ2u+Δu+u·u=g(x,t),u|t=τ=uτ

Kuramoto-Sivashinsky方程; 一致吸引子; 一致有界性; 收敛性

令ρ∈[0,1]和ε>0,考虑如下Kuramoto-Sivashinsky方程

(1)

(2)

不失一般性,定义

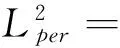
u(x+2dei,t),x∈Ω,t≥0.i=1,2},

mu(x+2dei,t),x∈Ω,t≥0.i=1,2},

m=1,2.

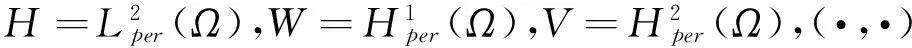
1 预备知识

为了证明本文的主要结论,下面的概念和抽象结果是需要的,详细内容请看文献[8-9].

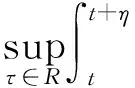
(3)

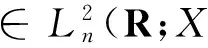
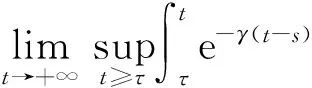
(4)

关于φ∈H(φ0)一致.

假设1令{T(h)|h≥0}是作用在符号空间Σ上的一族算子,满足

i) T(h)Σ=Σ,∀h∈R+;

ii) 平移恒等式,

Uσ(t+h,τ+h)=UT(h)σ(t,τ),∀σ∈Σ,t≥τ,τ∈R,h≥0.

引理2[9]设E是一致凸Banach空间,则满足假设1的过程族{Uσ(t,τ)},σ∈Σ在E中有紧的一致(关于σ∈Σ)吸引子AΣ,且

AΣ=ω0,Σ(B0)=ωτ,Σ(B0),∀τ∈R,

如果它满足

i) 有有界一致(关于σ∈Σ)吸收集B0;

ii) 满足一致(关于σ∈Σ)条件(C).

进一步,如果E是一致凸Banach空间或Hilbert空间,定理的逆也成立.

2 一致吸引子的存在性

2.1 一致吸收集

为了证明方程(1)和(2)的一致吸引子,先证明方程

(5)

一致吸引子的存在性.

u(t)∈C(Rτ;V),∂tu∈C(RT;H).

(6)

证明根据标准的Galerkin方法[11]，很容易得到解的存在唯一性.

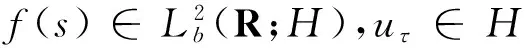
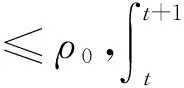
(7)

(8)

所以

‖u(t)‖2≤‖uτ‖2e-α1(t-τ)+

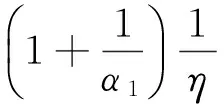
另外,对式(8)从t到t+1积分得

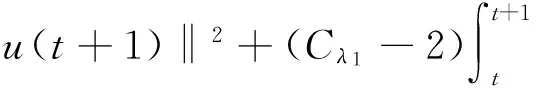
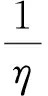
从而

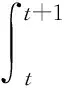
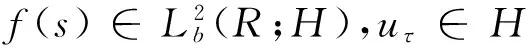
‖u(t)‖‖Δu(s)‖2ds≤I1.

(9)

证明在H中用-Δu与(5)作内积,并利用Cauchy不等式得

(10)

取α2=Cλ1-2-η>0,则上式变为:

(11)

对式(11)从s到t积分,其中,t-1≤s≤t,

‖u(t)‖2≤‖‖,

再对上式关于s从t-1到t积分得

‖‖‖.

令t1=t0+1,则当t≥t1时,

‖‖,

由式(10)得

(12)

对式(12)从t到t+1积分得

‖u(t+1)‖2-‖u(t)‖2+

因此

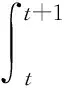
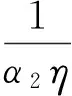
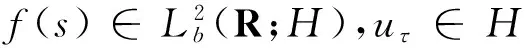
‖Δu(t)‖≤ρ2.

(13)

证明在H中用Δ2u与(5)作内积,并利用Cauchy不等式得

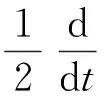
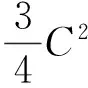
故

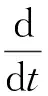
(14)

对式(14)从s到t积分,其中,t-1≤s≤t,

再关于s从t到t+1积分得

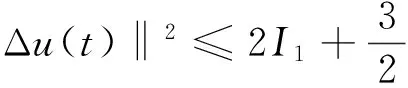
取t2=t1+1,则当t≥t2时

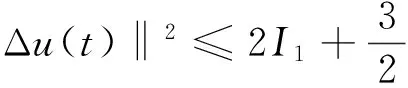
2.2 一致吸引子

AH(f0)=ω0,H(f0)(B1)=ωτ,H(f0)(B1),

(15)

其中,B1是空间V中的有界一致(关于f∈H(f0))吸收集.

证明由定理4和引理2可知,只需证明过程族Uf(t,τ),f∈H(f0)在空间V中满足一致(关于f∈H(f0))条件(C).

0<λ1≤λ2≤…≤λj≤…,j→∞,λj→+∞,

(16)

Aωj=λjωj,∀j∈N.

设Vm=span{ω1,…,ωm}是空间V的m维子空间,Pm:V→Vm是标准正交投影.对任意的u∈D(A)可分解为:

u=Pmu+(I-Pm)uu1+u2.

(17)

在空间V中用Au2与(5)式做内积,可得

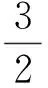
进一步,

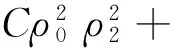
(18)

由引理2,当m充分大时,对任意的ε>0,

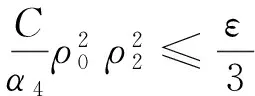
因此

‖Δu2‖2≤ε,∀t≥T,f∈H(f0),

从而过程族Uf(t,τ),f∈H(f0)在空间V中满足一致(关于f∈H(f0))条件(C).

2.3 吸引子Aε的一致有界性

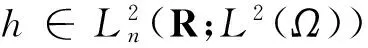
(19)

的解,其中,ε∈(0,1],且满足不等式

‖Δv(t)‖2≤Cε.

(20)

根据Gronwall引理得

证明令u是方程(1)在初值uτ∈V下的解.对∀ε>0,考虑方程

(21)

类似定理6,有

‖Δv(t)‖2≤Cε1-ρ,

(22)

令w(t)=u(t)-v(t),则w(t)是满足方程

wt+Δ2w+Δw+B(w+v,w+v)=

g(x,t),w|t=τ=uτ.

(23)

再用w与式(23)作内积,可得

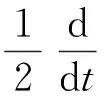
|b(w+v,v,w)|+(g(x,t),w),

估计三线性型b(w+v,v,w),

|b(w,v,w)|≤C‖w‖·‖Δw‖·‖Δv‖≤

|b(v,v,w)|≤C‖v‖·‖Δv‖·‖Δw‖≤

2C‖w‖2‖Δv‖2+2C‖v‖2‖Δv‖2+2C‖g‖2,

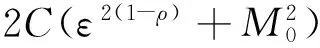
‖w(t)‖2≤

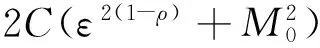
由u=w+v和式(22)可得

(24)

因此,过程族Uε(t,τ)有一个不依赖于ε的吸收集B*.由于Aε⊂B*,则定理得证.

3 一致吸引子的收敛性

为了证明定理8,首先需要比较当初始值相同时,方程(1)和(2)的解.记

uε(t)=U(t,τ)uτ,

其中,uτ属于吸收集B*.由式(24)可得一致估计,

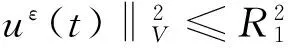
(25)

特别地,当ε=0时,由于uτ∈B*,则有

(26)

其中,R0=R0(ρ),因为B*的大小依赖于ρ.

定理9对∀ε∈(0,1],τ∈R和∀uτ∈B*,令

w(t)=uε(t)-u0(t),

(27)

其中,uε(0)=u0(0)=uτ,对任意的不依赖于ε的常数C,满足

证明由于误差w(t)是方程

wt+Δ2w+Δw+B(uε,uε)-B(u0,u0)=

的解.

令q(t)=w(t)-v(t),其中,v(t)是方程(21)的解,则q(t)满足

qt+Δ2q+Δq+B(uε,uε)-B(u0,u0)=0,

q|t=τ=0,

(28)

注意到

(B(uε,uε)-B(u0,u0),q)=b(u0,v,q)+

b(q,u0,q)+b(v,u0,q)+b(q,v,q)+b(v,v,q),

所以,用q与式(28)作内积得

2C(‖Δu0‖2+‖Δv‖2)‖q(t)‖2+

再用Δ2q与式(28)作内积得

C(‖Δu0‖2+‖Δv‖2+

(29)

由w=q+v和式(22)可得

为了研究一致吸引子的收敛性,实际上需要定理9更一般的形式,其对应的方程簇为:

(30)

对任意的ε∈(0,1],令

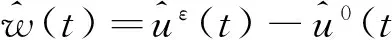
定理10如下不等式成立,

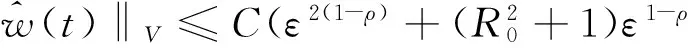
且

结合定理10,当t=0和τ=-L时,有

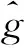
令L=T,结合上述两个不等式,可得

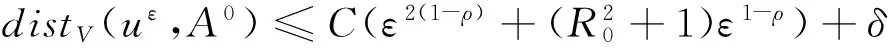
由于uε∈Aε是任意的,则

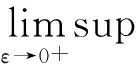
其中,δ>0是任意的常数,证毕.

[1] KURAMOTO Y. Difusion induced chaos in reaction systems[J].Progr Theoet Phys Suppl, 1978, 64:346-367.

[2] SIVASHINSKY G. On flame propagation under conditions of stoichiometry[J].SIAM J Appl Math, 1980, 64:67-82.

[3] GUO B L, SU F Q. The global attractors for the periodic initial value problem of generalized Kuramoto-Sivashinsky type equations in multi-dimensions[J].J Partial Diff Eqs, 1993, 6:217-236.

[4] GUO B L, GAO H J. Global attractor for axially symmetric Kuramoto-Sivashinsky equation in annular domains[J].J Math Study, 1996, 29:1-4.

[5] 王冠香, 刘曾荣. Kuramoto-Sivashinsky 方程的渐近吸引子[J].应用数学学报, 2000, 23:329-336.

[6] WANG S Y, MU L G,ZHANG Y H. Global attractors of strong solution for the generalized Kuramoto-Sivashinsky equation[J].Chinese Quart J Math, 2008, 23:75-82.

[8]LUSS,WUHQ,ZHONGCK.Attractorsfornon-autonomous2DNavier-Stokesequationswithnormalexternalforce[J].DiscrContDynSys, 2005, 13:701-719.

[9]MAQF,WANGSH,ZHONGCK.Necessaryandsufficientconditionsfortheexistenceofglobalattractorsforsemigroupsandapplications[J].IndianaUnivMath, 2002, 51:1541-1557.

[10]ANHACT,TOANBND.NonclassicaldiffusionequationsonRNwith singularly oscillating external forces[J].Applied Mathematics Letters, 2014, 38:20-26.

[11] BABIN A V, VISHIK M I. Attractors of Evolution Equations[M]. Amsterdam:North-Holland, 1922.

ut+Δ2u+Δu+u·u=g(x,t)+ε-ρh(t/ε),u|t=τ=uτ

forρ∈[0,1] andε>0 and the corresponding K-S equation:

ut+Δ2u+Δu+u·u=g(x,t),u|t=τ=uτ, as ε=0.

Furthermore, the uniform (w.r.t.ε) boundedness of a class of uniform attractorsAεare verified as well as the convergence of the attractorsAεfor the first equation to the attractorA0of the second one asε→0+.

Existence,uniform boundedness and convergence of uniform attractors for the non-autonomous Kuramoto-Sivashinsky equations

SHEN Xiaoying, MA Qiaozhen

(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070)