不同Mg掺杂位置对ZnO电子结构、态密度和光学性质的影响

毛彩霞， 黄海铭， 胡永红，3*

(1.湖北科技学院 核技术与化学生物学院， 湖北 咸宁 437100; 2.湖北汽车工业学院 理学院， 湖北 十堰 442002; 3.南京理工大学 材料科学与工程学院， 南京 210094)



不同Mg掺杂位置对ZnO电子结构、态密度和光学性质的影响

毛彩霞1， 黄海铭2， 胡永红1，3*

(1.湖北科技学院 核技术与化学生物学院， 湖北 咸宁 437100; 2.湖北汽车工业学院 理学院， 湖北 十堰 442002; 3.南京理工大学 材料科学与工程学院， 南京 210094)

通过第一性原理计算， 研究了替代位和间隙位Mg掺杂对ZnO电子结构、态密度和光学性质的影响. 结果表明， 替代位Mg掺杂导致ZnO带隙展宽， 而间隙位Mg掺杂ZnO形成n型半导体. 比较了纯ZnO和不同Mg掺杂位置MgZnO体系的分波和总电子态密度， 并解释了相应的电子结构和光学性质的差别. 发现替代位Mg掺杂和纯ZnO体系的光学特性差别较小， 而间隙位Mg掺杂导致ZnO光吸收边蓝移， 折射率减小， 而且在可见到近紫外光区域 (0到4.2 eV)， 具有比纯ZnO更好的光透过性.

第一性原理计算; 电子结构; 态密度; 光学性质; MgZnO

ZnO是一种直接带隙的半导体光电材料， 室温禁带宽度为3.37 eV， 自由激子束缚能为60 meV， 远大于GaN的结合能(25 meV)[1]. ZnO还具有生长温度低， 抗辐射性能好， 环境友好和价格便宜等特点[2]， 是具有重要发展和应用潜力的半导体材料， 可能在短波长发光二极管、激光器和太阳能电池等领域得到广泛应用. 近年来， 人们发现通过掺杂可以改变ZnO 的性质， 在实验上已有许多相关的报道[3]. 例如， 对其掺杂Al， Ga和In等元素可得到导电性能较好的n型ZnO薄膜材料[4]. 过渡金属元素Ni， Cu和Mn等掺杂ZnO， 可以获得居里温度高于室温的稀磁特性[5]. 但是， 人们对掺杂结构以及掺杂后的电学、光学和磁学性质变化的机理还不是很清楚， 因此最近对于ZnO 掺杂的理论研究已成为该领域的一个研究热点[6-7]. 实验研究发现， 在ZnO中掺杂不同量的Mg， 可以调控它的电子结构和光电性质 (例如， 禁带宽度可能从3.37 eV调到7.8 eV). 由于Mg2+离子半径(0.1057 nm) 和Zn2+离子半径(0.1060 nm) 较为接近， 其掺入后晶格常数的变化仅在1% 左右. 目前普遍认为Zn1-xMgxO是与ZnO 构建有效异质结的理想三元合金体系， 这使Zn1-xMgxO合金成为紫外波段光电器件研究的热点方向.

目前， 第一性原理计算是电子结构计算较为准确的理论方法，大量的第一性原理计算工作， 报道了Mg掺杂ZnO的晶体结构和光电性质随掺杂浓度的变化. 这些研究使得我们对Mg掺杂行为和MgZnO合金的几何结构和电子结构以及光学性质有了一定的了解. 以往对Mg掺杂的ZnO的第一性原理计算研究都是基于Mg替代Zn位置的超晶胞模型. 对间隙位掺杂Mg的ZnO模型及其光电学性质的研究结果很少有报道. 然而实验研究表明，ZnO中Mg掺杂制备MgZnO纳米晶或薄膜时， 不管Mg掺杂浓度是多少， 总有一部分Mg原子可能处于纤锌矿结构ZnO晶格的间隙位置. 而且这些处于间隙位置处的Mg原子会影响整个体系的晶格常数和相应体材料或薄膜的电学和光学性质[8-10]. 因此， 对间隙位Mg掺杂ZnO进行第一性原理计算研究具有重要理论意义， 并可能对MgZnO的能带工程及其光电材料的制备具有重要的参考价值. 本文计算了纤锌矿结构的ZnO晶体中掺杂Mg后体系的电子态密度和光学性质. 研究了掺杂位置不同的两种MgZnO晶体的介电函数、折射率、吸收光谱和反射光谱等光学性质的变化， 并对其进行了理论分析和比较. Mg在纤锌矿结构ZnO中的间隙位掺杂位置可以有四面体间隙位和八面体间隙位两种， 因为杂质原子在八面体间隙位处稳定性比四面体间隙位高， 所以本文只考虑了Mg在ZnO中的八面体间隙位置掺杂情况．

1 计算模型和方法

计算采用3×3×2的纤锌矿ZnO超晶胞， 由36个ZnO单胞组成， 共72个原子.1个镁原子替换超晶胞中的锌原子， 对应掺杂浓度为2.78%， 或者1个镁原子占据超晶胞中的一个八面体间隙位置， 对应掺杂浓度为2.7%. 掺杂后的超晶胞结构见图1．

绿色、灰色和红色的球分别代表Mg、Zn和O原子,“I”代表八面体间隙位置，“S”代表替代位置．图1 掺Mg的3×3×2纤锌矿ZnO超晶胞结构.Fig.1 The 3×3×2 wurtzite ZnO supercells doped with Mg atoms

计算采用密度泛函理论下的第一性原理平面波赝势方法， 电子间相互作用的交换-关联能采用广义梯度近似(GGA)修正方法(PBE). 为准确计算带隙值， 对Zn 3d轨道引入壳上库伦相互作用(U=7.5 eV)[11-12]. 平面波截止能Ecutoff选取为380 eV， k网格点选取4×4×3[13-14]. 在自洽场运算中， 自洽场设为1×10-6eV/atom. 结构优化计算采用BFGS算法[15]， 优化参数为: 原子间的相互作用力收敛标准设为: 0.05 eV/Å; 单原子能量的收敛标准设为: 2×10-5eV; 晶体内应力的收敛标准设为: 0.1 GPa; 原子最大位移收敛标准设为: 0.002 Å[3，6，8]. 四个参数同时进行优化， 且最后均达到收敛标准. 参与计算的价态电子分别为: Mg：2s22p2; Zn：3d104s2; O：2s22p4. 对于光学性质的计算， 引入了剪刀算符校正(修正值等于能带的实验测量和理论计算值之差). 对纯ZnO， 替代位掺Mg和间隙位掺Mg的ZnO 3种模型， 所取剪刀因子值分别为2.456、2.450和2.720 eV．

2 结果与讨论

2.1 电子结构和态密度

图2是纯ZnO、Mg替代Zn掺杂和Mg八面体间隙位掺杂ZnO的能带结构. 从图2(a)可知纯ZnO的最小带隙Eg约为0.919 eV， 比实验值(3.37 eV)低得多， 这主要是由于广义梯度近似与局域密度近似都存在Eg计算值偏低的普遍性问题[16]. 对ZnO晶体而言， 主要是计算中过高的估计了Zn 3d的能量， 造成Zn 3d和O 2p相互作用的增大， 结果使价带带宽增大， 带隙偏低， 但这并不影响对ZnO电子结构的理论分析. 从图2(b)可以看出， Mg替位掺杂后， 导带向高能端略有移动， 所以带隙值增大. 从图2(c)可以看出， Mg间隙位掺杂后， ZnO的费米能级向上移动并进入导带内， 很显然这是Mg掺入后电子数增多所引起的. 纯ZnO， Mg替代Zn掺杂和Mg八面体间隙位掺杂ZnO最小带隙宽度分别为0.919和0.972，0.747 eV．

图2 能带结构Fig.2 The energy band structures

为了分析Mg掺杂对ZnO电子结构的影响， 以及不同Mg掺杂位置的区别， 我们对理想ZnO晶体、Mg替代Zn位置和Mg占据八面体间隙位置的ZnO晶体的电子态密度， 包括分波态密度(PDOS)和总态密度(TDOS)进行了计算(如图3-图5). 图中虚线位置表示费米能级. 图3是纯ZnO的分波态密度和总态密度图. 由图3可知， 纯ZnO上价带主要由O 2p态和Zn 3s， 3p和4s态贡献， 其中价带顶位置由O 2p态决定. 它的导带底位置由Zn 4s态决定.

图3 纯ZnO的分波态密度和总态密度图Fig.3 The total and partial density of states of pure ZnO

图4是Mg替代位掺杂ZnO的分波态密度和总态密度图. 由图4可知， 价带顶的位置主要由O 2p态决定， 导带底的位置则主要由Zn 4s态决定. 从图3和图4不难看出， 价带和导带中增加了Mg的2s和2p态， 而价带中Zn 3d态相对变少， 价带宽度变窄. 导带中Mg 2s和2p态较Zn 4s态的能量位置高， 所以Mg替代Zn掺杂后， 导带底向高能端移动. 因此， 带隙宽度较理想ZnO晶体的带隙变宽. 从图4还可以看出来， Mg原子和Zn原子态密度有5点区别：(1) 导带中Mg 2p态和Zn 3p态都较Zn 4s态远离费米能级一些(大约1 eV);(2) 在价带的-4.5到-2.5eV范围内， Zn的4s态的峰强度要比Mg的2s态的峰强度大2倍左右;(3) Zn的3d态在-10到-7.5 eV范围内有很强的峰;(4) Zn的4s、2p和3d态比Mg的2s和2p态对上价带的贡献要大一些; (5) 在能量区间(-17，-16)eV内， Zn的4s、2p和3d态与Mg的2s态一样， 都有几乎同样微弱的峰， 而此能级主要由O的2s态贡献．

图5是Mg八面体间隙位掺杂ZnO的分波态密度和总态密度图. 从图5看出， 费米面进入导带， 这是因为Mg间隙原子的引入增加了电子数. 从图4和图5可以看出， 替代Zn位置的Mg和处在八面体间隙位置的Mg的分波态密度有几点差别: (1) 在低能端， 处在间隙位置的Mg 2p态较替代Zn位置的Mg 2p态强度大0.5倍， Mg 2s和2p态峰能量位置间距变大. (2)在价带中， 间隙位置Mg较替代位置Mg的2s， 2p态峰位更远离导带底， 峰强度更强. 尤其两种情况下Mg的2p态的主峰峰位差别显著. (3) 在导带中， 间隙位置Mg较替代位置Mg的2s态峰位更靠近价带顶， 且各峰强度更强．

图4 Mg替代位掺杂ZnO的分波态密度和总态密度图Fig.4 The total and partial density of states of ZnO doped by substitutional Mg

图5 Mg间隙位掺杂ZnO晶胞的分波态密度和总态密度Fig.5 The total and partial density of states of ZnO doped by interstitial Mg

2.2 光学性质

在线性响应范围内， 固体宏观光学响应函数通常用光的复介电函数ε(ω)=ε1(ω)+iε2(ω)来描述， 其中，ε1=n2-k2， ε2=2nk.介电函数虚部ε2(ω)可以利用计算占据态和非占据态波函数的矩阵元得到， 介电函数的实部ε1(ω)则可以利用Kramers-Kronig色散关系求出. 吸收系数、反射率和能量损失谱就可以由ε1(ω)和ε2(ω)推导得出. 介电函数是沟通带间跃迁微观过程和固体电子结构的桥梁， 它包含固体能带结构和光谱方面的信息. 图6 是纯ZnO， Mg替代位和间隙位掺杂的ZnO的介电函数虚部ε2(ω). 从图6可以看出， 替代位Mg掺杂的ZnO的虚介电函数谱和纯ZnO的有微小差别， 而间隙位Mg掺杂的ZnO的虚介电谱则与前两者有显著的区别. 首先是低能端吸收边有大约2 eV的蓝移， 其次介电峰个数变少了， 再次主峰强度明显变强. 以上3种情况下介电函数虚部的各峰能量位置列表在表1中.

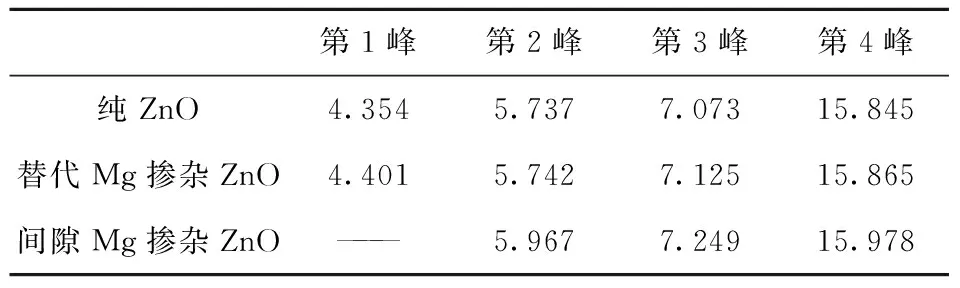
表1 3种ZnO材料的虚介电谱的各峰能量位置.

介电函数虚部与吸收有关， 各介电峰可以从态密度图结合电子跃迁进行解释. 第一个介电峰对应价带顶到导带底的跃迁. 从图6可看出， 替代位Mg掺杂的ZnO虚介电函数谱的第一峰强度要比纯ZnO的弱， 峰的能量位置有向高能区域的微小移动(蓝移)， 而间隙位Mg掺杂情况下ZnO的虚介电函数谱在此能量范围内没有出现介电峰. 前者是因为在Mg替位掺杂情况下， 导带底Zn 4s态总峰强度减弱， 且峰位有微弱蓝移. 后者是因为Mg间隙位掺杂形成n型ZnO， 费米面高于导带底， 导带底到费米能级处被电子填充， 相应的电子从价带跃迁到费米能级以上位置处能量增大， 介电函数虚部的吸收边向高能端移动， 故使光学吸收阈变大. Mg掺杂后ZnO的介电峰减少了. 从态密度图可以看到， 间隙位Mg离子引入后， Mg 2s， 2p与Zn 3d， O2p电子发生杂化作用， 使得价带和导带展宽， 相应的带间跃迁的能量取值范围扩大， 造成介电吸收相应变得分散， 使得介电吸收峰减少. 第2个峰主要对应价带中的Zn3d 态到O2p态的跃迁. 纯ZnO和Mg替位掺杂的ZnO的第2介电峰峰位和峰强相近. 间隙位Mg掺杂的ZnO的第2介电峰峰位相对纯ZnO和替代位掺Mg的ZnO约有0.2 eV的蓝移. 这是因为替代位Mg掺杂情况下价带中靠近低能端的O2p态的峰位较间隙位Mg掺杂情况下相应的O 2p态峰位更靠近Zn 3d 态峰位. 第3个峰主要对应价带中的O 2s态到Zn 3d态的跃迁. 纯ZnO和Mg替位掺杂的ZnO的第3介电峰峰位和峰强几乎完全相同. 间隙位Mg掺杂的ZnO的第3介电峰峰位相对替代位掺Mg的ZnO的峰强度略强， 并且峰位约有0.12eV的蓝移. 这是因为间隙位Mg掺杂情况下相应的Zn3d态峰强度更强， 且Zn 3d态峰位相对替代位情况下的峰位有微弱蓝移. 第4个峰主要对应价带中的O的2s态到上价带中的Zn的3d和3p态以及Mg的2p态的跃迁. 纯ZnO和Mg替位掺杂的ZnO的第四介电峰峰位和峰强完全类似. 间隙位Mg掺杂的ZnO的第4介电峰峰位相对替代位掺Mg的ZnO的峰位有微弱的蓝移. 这可能是因为理论计算的误差引起的.

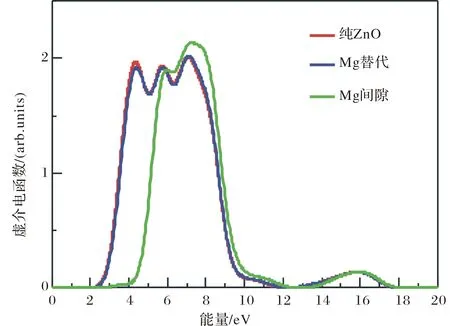
图6 纯ZnO和Mg替代位和间隙位掺杂的ZnO材料的虚介电谱Fig.6 The imaginary part of dielectric functions of the pure ZnO and ZnO materials doped by substitutional and interstitial Mg

(a)吸收谱， (b)反射谱，(c)消光系数谱， (d)能量损失谱图7 纯ZnO和Mg替代位及间隙位掺杂后的ZnO的光学吸收谱、反射谱、消光系数谱和能量损失谱Fig.7 The absorption coefficients， reflectivity coefficients， extinction coefficients and energy loss functions of pure ZnO and ZnO doped by substitutional and interstitial Mg

图8 纯ZnO和Mg替代位及间隙位掺杂后的ZnO的光学折射率Fig.8 The refractive index of pure ZnO and ZnO doped by substitutional and interstitial Mg

材料的吸收系数表示光波在介质中传播单位距离光强度衰减的百分比. 图7(a)为3种材料的吸收光谱. 纯ZnO和Mg替代位掺杂的ZnO的吸收系数在小于1.46和1.56 eV范围内为零，在可见到近紫外范围(1.7～3.1 eV)较小. Mg间隙位掺杂的ZnO的吸收系数在小于1.56 eV范围内为零， 在可见到近紫外范围(1.7～4.2 eV)较小. 另外， 从图7(b)和(c)可以看出， Mg间隙位掺杂的ZnO的反射率谱和消光系数谱在可见到近紫外范围内的强度可近似为零， 远小于纯ZnO和Mg替代位掺杂ZnO的相应强度. 所以可得出结论， 在可见到近紫外范围内， Mg间隙位掺杂的ZnO的光透过性要比前两者好. 从图7(d)可以看出3种材料的主能量损失峰分别位于9.611 9， 9.604 6和9.772 7 eV处， 能量损失峰和反射谱的急剧下降相对应. 图8是3种材料的折射率谱. 可见， 纯ZnO， Mg替代位和间隙位掺杂ZnO的折射率n0分别为1.463， 1.456和1.320. 从图6～图8可以看出这3种材料的光谱有一个共同的特点， 即在高于10 eV的能量范围里， 它们的峰位和强度非常一致.

3 结论

本文采用基于密度泛函理论的平面波赝势方法和广义梯度近似， 详细计算并讨论了Mg替代位和间隙位掺杂ZnO体系的电子结构和光学性质. 比较了掺杂前后以及不同Mg掺杂位置的ZnO的偏态密度和总态密度的变化， 发现替代位Mg掺杂ZnO的带隙较纯ZnO的带隙大， 而间隙位Mg掺杂ZnO后， 其费米能级进入导带， 形成n型半导体， 最小光学带隙为0.747 eV. 通过光学常数计算， 发现替代位Mg掺杂ZnO跟纯ZnO的光学性质差别较小，而通过间隙位Mg掺杂， 可以有效提高可见光区到近紫外区域的光透过率. 同时间隙位Mg掺杂导致ZnO光吸收边向高能端移动， 折射率减小， 所以间隙位Mg掺杂可以明显的改变ZnO的光学性能．

[1] TANG Z K， WONG G K L， Yu P， et al. Room-temperature ultraviolet laser emission from self-assembled ZnO microcrystallite thin films [J]. Appl Phys Lett， 1988， 72: 3270-3274．

[2] OZGUR U， ALIVOV Y I， LIU C， et al. Comprehensive review of ZnO materials and devices [J]. Journal of Applied Physics 2005， 98: 041301(1-5)．

[3] 刘建军. 掺Ga对ZnO电子态密度和光学性质的影响 [J]. 物理学报， 2010， 59(9): 6466-6472．

[4] LU J G， FUJITA S， KAWAHARAMURA T， et al. Carrier concentration dependence of band gap shift in n-type ZnO：Al films [J]. J Appl Phys， 2007， 101: 083705(1-6)．

[5] VENKATESAN M， FITZGERALD C B， LUNNEY J G， et al. Anisotropic ferromagnetism in substituted zinc oxide [J]. Phys Rev Lett， 2004， 93：177206(1-4)．

[6] 邓胜华， 姜志林. F， Na共掺杂p型ZnO的第一性原理研究 [J]. 物理学报， 2014， 7: 077101(1-5).

[7] WANG Q， SUN Q， JENA P， et al. First-principles study of magnetic properties in V-doped ZnO [J]. Appl Phys Lett， 2007， 91: 063116(1-5)．

[8] 侯清玉， 赵春旺， 金永军， 等. ZnO高掺杂Ga的浓度对导电性能和红移效应影响的第一性原理研究 [J]. 物理学报， 2010， 59(6):4157-4161．

[9] TRUNK M， VENKATACHALAPATHY V， KUZNETSOV A Y. Deep level related photoluminescence in ZnMgO [J]， Applied Physics Letters， 2010， 97: 211901(1-3)．

[10] GINTING R T， YAP C C， YAHAYA M， et al. Improvement of inverted type organic solar cells performance by incorporating Mg dopant into hydrothermally grown ZnO nanorod arrays [J]， Journal of Alloys and Compounds 2014， 585: 696-702．

[11] SCHLEIFE A， EISENACHER M， RÖDL C， et al. Ab initio description of heterostructural alloys: Thermodynamic and structural properties of MgxZn1-xO and CdxZn1-xO [J]， Phys. Rev B 2010， 81：245210 (1-3)．

[12] GUAN L， LIU B T， LI Q， et al. Electronic structure and optical properties of substitutional and interstitial phosphor-doped ZnO [J]. Physics Letters A， 2011， 375: 939-945．

[13] MONKHORST H J， PACK J D. Special points for Brillouin-zone integrations [J]. Phys Rev B， 1976， 13: 5188-5196．

[14] PACK J D， MONKHORST H J. “Special points for Brillouin-zone integrations”—a reply [J]. Phys Rev B， 1977， 16: 1748-1749．

[15] FISCHER， T H， ALMLÖF， J. General methods for geometry and wavefunction optimization [J]. J Phys Chem， 1992， 96: 9768-9774．

[16] OSUCH K， LOMBARDI E B， GEBICKI W. First principles study of ferromagnetism in Ti0.0625Zn0.9375O [J]. Phys Rev B， 2006， 73: 075202(1-5)．

The influences of different Mg-doping positions on the electronic structure，density of state and optical properties of ZnO

MAO Caixia1， HUANG Haiming2， HU Yonghong1，3

(1.School of Nuclear Technology and Chemistry & Biology， Hubei University of Science and Technology，Xianning， Hubei 437100; 2.School of Science， Hubei University of Automotive Technology，Shiyan， Hubei 442002; 3.College of Materials Science and Engineering， Nanjing University of Science and Technology， Nanjing 210094)

The electronic structure, density of states and optical properties of ZnO doped by Mg in substitutional and interstitial positions are studied through the first-principle calculations. It is found that the band gap of ZnO is extended by doping Mg in the substitutional position, and that ZnO doped by Mg in interstitial position becomes n-type semiconductor. The partial and total electronic state density of pure ZnO and ZnO doped by Mg in different positions are compared. The differences between their electronic and optical properties are explained. It’s found that the difference between the optical properties of pure ZnO and ZnO doped by Mg in substitutional position is non-significant. However, Mg-doping in interstitial position results in blue shift of the absorption edge and decrease of refractive index. In addition, their photo permeability in the energy range from visible to near ultraviolet (0～4.2 eV) is better than that of pure ZnO.

first-principle calculation; electronic structure; state density; optical property; MgZnO

2015-09-02.

江苏省博士后基金资助项目(1302099C);湖北科技学院教学研究项目(2013-XA-012)．

1000-1190(2016)02-0190-06

O481.1

A

*通讯联系人. E-mail: hchyh2001@tom.com.