第一性原理研究C/Si比对SiC理想剪切强度的影响

苏 文， 李盈盈

(1.武汉大学 动力与机械学院， 武汉 430072； 2.国核(北京)科学技术研究院， 北京 100029)



第一性原理研究C/Si比对SiC理想剪切强度的影响

苏 文1*， 李盈盈2

(1.武汉大学 动力与机械学院， 武汉 430072； 2.国核(北京)科学技术研究院， 北京 100029)

使用第一性原理计算方法研究C/Si比对β-SiC的理想剪切强度的影响，建立化学计量比下理想β-SiC分子模型，用C原子替换其中的Si原子，经蒙特卡罗方法优化得到非化学计量比下的SiC分子模型，这些晶体的C/Si比的变化范围是1～1.52.每个模型样品都沿[100]方向剪切，得到其剪切应力应变关系，最终了解C/Si比对SiC理想剪切强度的影响.计算结果表明，随着C/Si比增加，SiC的理想强度总体上呈下降趋势.在剪切载荷逐渐增大情况下，晶体会在C团簇周围的C-C键或者C-Si键处断裂.C原子的聚集，会使SiC的剪切强度减少，因为C团簇内部存在应变，而且C团簇越大，SiC的剪切强度下降得越剧烈.

理想剪切强度； 第一性原理； 蒙特卡罗模拟； SiC； C团簇； 非化学计量比

SiC由于拥有众多的优点，如热导系数高、热膨胀系数低、抗热冲击能力强、高温下抗腐蚀性能好、中子吸收截面低以及高温下能保留裂变气体等，而被认为是未来理想的核材料[1].然而纯SiC也有其致命的缺点，如断裂韧性差、对微观结构中的缺陷非常敏感、脆性及可靠性低，这些缺点是其应用在实际工程之中的最大阻碍.为了克服纯SiC的缺点，科学家们将纯SiC通过连续SiC纤维的强化，形成了SiC/SiC陶瓷基复合材料.这种SiC/SiC复合材料与纯SiC相比，强度、硬度、抗损伤能力都有所增强，并且对于缺陷和刻痕毫不敏感，这使得它能够适用于恶劣的裂变反应堆堆芯环境[2].同时SiC/SiC复合材料的诱导放射性低，固有活性低、衰变热低及氚渗透性低，使得其也能应用于聚变系统中[3].种种的优点都使得SiC/SiC复合材料在第四代反应堆和聚变堆设计中都备受瞩目.

经过几十年的发展，SiC/SiC复合材料已经形成了具有特色的三代，每一代性能的增强都是通过改进SiC纤维的性能来达到的，因为SiC纤维对复合材料的抗辐照性、高温强度和稳定性都至关重要[4]，因此更深入了解SiC的性质对于制造出高性能的SiC/SiC复合材料是必不可缺的.科研人员们为了提高SiC的抗辐照性和高温下的性能，这些年来研发SiC纤维的趋势是寻找靠近化学计量比、氧含量低、结晶度高的SiC纤维[5-7]，因为这样的SiC纤维在中子辐照下其机械性能不会降低[6].但是，有些在化学计量比附近、氧含量低的SiC纤维(如Hi-Nicalon Type-S)较其他类型的SiC纤维(如Hi-Nicalon)，强度却有所下降[4].换而言之，C/Si比对SiC的机械性质的影响我们还不清楚.

理想脆性断裂定义为原子键的断裂，因此理想强度是材料在断裂临界点处所受的应力值[8].理想强度的计算能够让我们从原子成键本质上了解材料的机械性能，因此，多年来不少科研工作者用计算的方法研究了SiC的机械性质.Lambrecht 等采用Orowan方程的方法研究了SiC的杨氏模量和剪切模量等性质，这些弹性常量的计算值与实验值比较接近[9].王自强等用第一性原理计算方法研究了β-SiC的弹性、稳定性、理想强度等性质[10].Yoshitaka等人也用第一性原理的方法研究了SiC的理想拉伸和剪切强度[11].虽然世界使用计算方法研究理想SiC性质的科研人员不在少数，但是大部分都是研究化学计量比下SiC的性质，并没有过多关注非化学计量比的SiC得机械性能，因此对C/Si比对SiC性能的影响也知之甚少.

李盈盈等[12]用第一性原理的方法研究了C/Si比对SiC理想拉伸强度的影响，得到C/Si比逐步增大，SiC的理想拉伸强度总体呈下降趋势.本文的研究内容，是在李的研究[12]上更进一步，使用第一性原理软件研究C/Si对SiC[100]方向上的理想剪切强度的影响.通过蒙特卡罗模拟的方法产生不同C/Si的非化学计量的SiC模型，再用第一性原理计算方法计算每个模型的应力应变曲线，最后了讨论C/Si比对SiCl理想剪切强度的影响.

1 计算方法

为了研究C/Si比对SiC理想强度的影响，首先需要建立不同C/Si比的SiC模型.相对于形成空位或者间隙原子这样的缺陷，C原子取代Si原子的形成能低得多，而Si原子取代C原子的形成能远高于其他缺陷[13]，因此我们的不同C/Si的SiC模型的建立是用C原子取代SiC晶体中的Si原子，经蒙特卡罗模拟优化形成的.由于工业实际用到的SiC中C/Si比均是大于1的[4]，因此我们构建了比例从1到1.52的10种比例的模型.计算采用3×2×2的超晶胞，每个单晶胞有4个C原子和4个Si原子，总共96个原子.用数量为1～10的C原子取代晶胞中的Si原子，构建10组非化学计量比的SiC晶胞，这些晶胞的C/Si比分别是1.04、1.09、1.13、1.18、1.23、1.29、1.34、1.4、1.46、1.52.每组根据取代的C原子所在晶胞中位置的不同，取5个不同的结构作为计算样品.

C原子取代Si原子的初始结构中，C原子只是简单地占据了Si原子的位置，此时的C-C键和C-Si键的长度相等，这并不是一个稳定的状态.因此，我们使用蒙特卡洛方法来优化C原子在结构中的位置[14]，使系统处于总能相对降低的亚稳定状态.系统总能是用大规模分子并行计算模拟器(LAMMPS)来计算的，蒙卡优化结构的过程如下：首先，随机地选择结构中目标数量Si原子，在选择的Si原子的位置上放上等量的C原子取代原来的Si原子；然后，随机选择相邻的两个原子，如果这两个原子的类型不同，一个C原子，一个Si原子，交换两个原子的位置后计算系统总能，如果交换位置之后总能下降，保留新结构，如果能量上升，保留原结构；如上重复1 000步以上，收敛的标准是平均每个原子能量小于10 meV，将最后的晶体结构用于剪切应力的计算，每个C/Si比比选择5个不同结构的计算样品以上.

图1所示的是C/Si比为1.09的晶胞结构.这个晶胞中有46个Si原子和50个C原子，黄颜色的大分子为硅原子，灰颜色的小分子为C原子，C原子数量为50,其中，A和B两个碳原子取代了硅原子的位置,晶体沿[100]方向剪切(箭头方向).

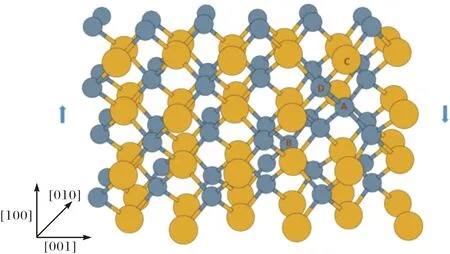
图 1 C/Si比为1.09的SiC超晶胞Fig.1 A SiC super cell with 50 C atoms and 46 Si atoms

系统总能的计算使用的是基于密度泛函理论(DFT)计算方法的第一性原理计算软件VASP[15-16]，核心区域附近的波函数是用投影增强波法[17]处理的.晶体波函数用平面波基展开，平面波动能的截止能是520 eV.对于所有C/Si比不同的样品，均选取(1×1×1)均匀网格的Monkhorst-Pack 类型的k点进行布里渊区的积分.

剪切应力应变曲线的计算过程中，应变过程是连续的，每一步初始结构均是在上一步弛豫完成后的结构上增加应变后得到的，每步增加的剪切应变为0.01.弛豫过程中，使用共轭梯度法最小化Hellmann-Feynman力，剪切[100]方向上的应变是固定的，使用准牛顿法使所有原子在其它方向上完全弛豫后，直到作用在所有原子上的力均小于0.05 GPa.从VASP 输出结果中， 可以直接得到弛豫后的原子位置、总能量、应力、应变等数据，剪切试验一直进行到有原子键断裂为止.

2 计算结果

2.1 化学计量比下SiC计算结果

我们首先计算了固体3C-SiC的平衡晶格常数、剪切模量、理想剪切强度，并将与实验数据和计算结果做比较，比较结果见表1.由于我们计算所用的晶体是没有任何缺陷的，而实际材料总存在缺陷，因此计算所得的强度值与实验值相比会高出一两个数量级.文章后面的部分也会介绍到非化学计量比下SiC的理想强度，这个值比没有缺陷的晶体材料值低得多，这也说明了缺陷确实会降低材料的理想剪切强度.

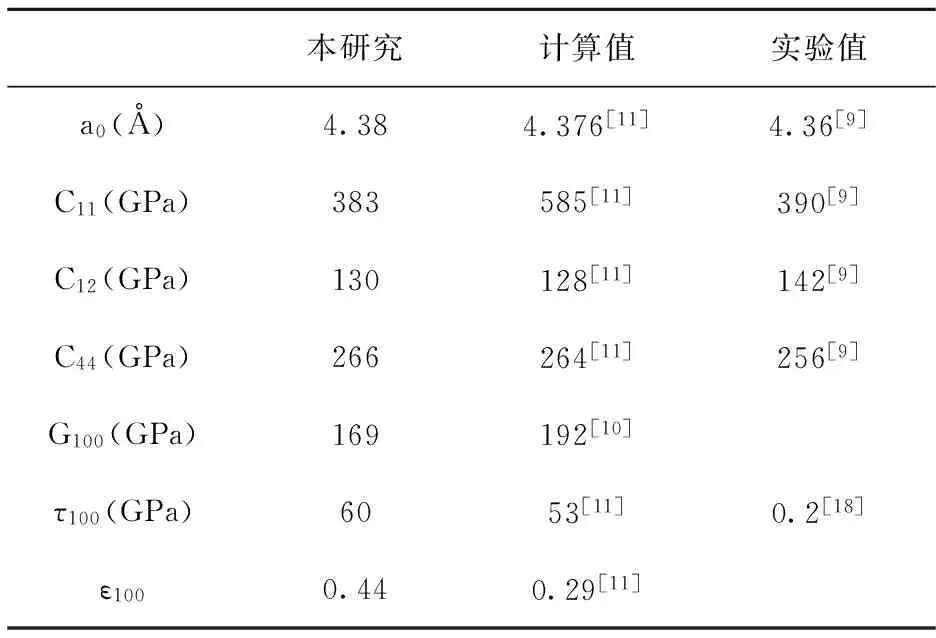
表1 β-SiC的平衡晶格常数a0，弹性常量C11、C12、C44，剪切模量G100，剪切强度τ100及相应的应变ε100

图2所示的是理想无缺陷的3C-SiC的应力应变曲线.应力开始随着应变的增加开始呈线性关系，在应变ε=0.13的时候出现一个极大值，随后应力随应变线性增加.忽略极大值出现的微小扰动，在ε<0.34时，应力随应变是线性变化的，发生的是弹性形变，弹性形变区的剪切模量为169 GPa.当ε>0.35时，此时材料出现非弹性形变，应力随应变增加至屈服强度后急剧下降，此时原子键发生断裂.β-SiC的理想强度为60 GPa，其发生原子键断裂相应的应变ε为0.44，在最大应力下，C-Si键的键长为2.15 Å，而在完全没有应力的情况下，C-Si键的键长为1.90 Å.

2.2 非化学计量比下SiC的计算结果

实际工业制造的SiC中，C浓度是要比Si的浓度高，为了研究C含量对SiC的影响，用C原子取代晶体中的Si原子，构建了10组C/Si比大于1的SiC模型.96个原子的超晶胞中，含有48个C原子和48个Si原子，分别用1～10个C原子取代等数量的Si原子，构建了C/Si比从1.04～1.52的10组SiC模型.每个比例选取5个不同结构作为计算的样品，每个结构经过蒙罗卡罗方法优化使系统能量最低，最后用第一性原理软件包VASP优化，优化后的同一C/Si比的计算样品的能量差别很小，小于10-3eV每个原子.

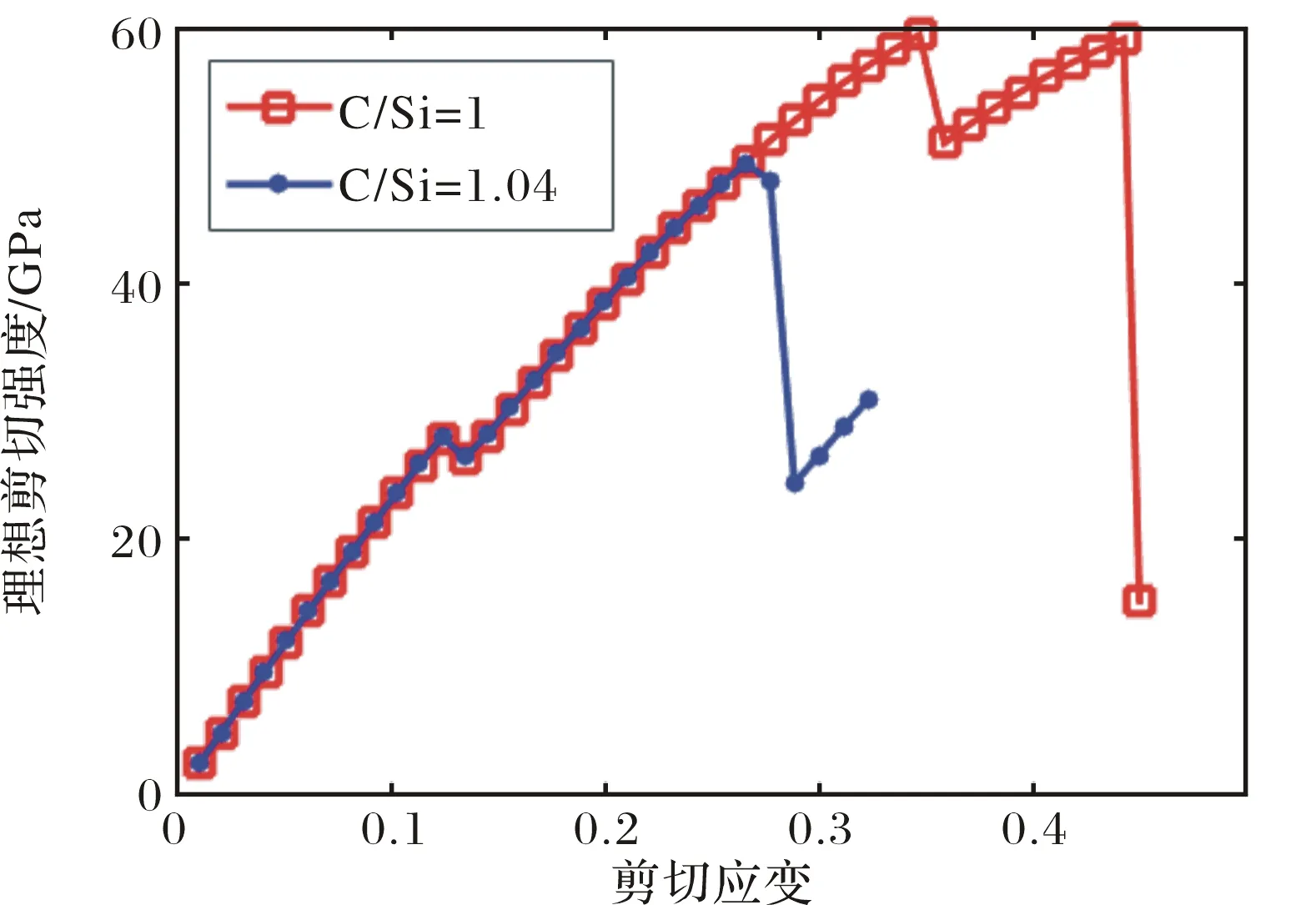
图2 理想3C-SiC和C/Si比为1.04的SiC样品的沿[100]方向上剪切的应力应变曲线Fig.2 The stress-strain curve of ideal 3C-SiC and a sample with the C/Si ratio 1.04 sheared along [100] direction

对于每一个样品，通过VASP计算得到沿[100]方向剪切的应力应变曲线.计算结果显示，C/Si比对SiC的剪切模量几乎没什么影响，从图2中也可以看出，不同C/Si比的应力应变曲线的斜率几乎是一致的.图2中所示的是C/Si为1.04的应力应变曲线和没有缺陷的β-SiC晶体的应力应变曲线.从图中可以比较得出，C/Si比为1.04的SiC的理想剪切强度比C/Si为1的明显低了许多.除此之外，无缺陷SiC在弹性形变之后，有一段非弹性形变，当应力超过非弹性形变的屈服强度后，原子键才发生断裂，应力突降，而C/Si比为1.04的SiC应力达到了弹性应变的最大之后，原子键就发生了断裂.这说明非化学计量比的SiC较化学计量比的SiC不仅强度下降了，而且变得更脆.每个比例的理想强度取五个样品计算结果的平均值，表2及图3列出了不同C/Si比SiC理想强度的平均值和标准差.

表2 不同C/Si比的SiC沿[100]方向上的理想剪切强度及相应的最大应变值

表2中列出了不同C/Si比SiC的理想剪切强度及相应的最大应变值.表中的理想强度为同一C/Si比5个不同结构理想剪切强度的平均值，强度的标准差为同一C/Si比5个不同样品的最大剪切应力的标准差，最大应变为同一C/Si比的5个样品最大剪切应力对应的应变的平均值，最大应变标准差则为这5个应变的标准差.从表中可以看出，β-SiC的理想强度随着C/Si比的增加总体上是呈现下降趋势的，但是不是严格的递减规律，原子键断裂的最大应变随C/Si比的增加总体上也是减小的.

图3所示的是SiC理想剪切强度随C/Si比变化曲线，曲线横坐标是C/Si比，纵坐标是SiC的理想剪切强度，图中以理想强度为中点的用黑线段也表示出了理想强度的偏差范围.从图中可以再出C/Si比从1增加到1.09的范围内，SiC的理想强度是急剧下降的，理想强度在为C/Si比1.09～1.40范围内的变化基本不大，曲线中出现了第1个平台，之后又下降，在C/Si比1.46后又出现第2个平台.总体上来看，SiC的理想剪切强度随C/Si比增加是呈现下降趋势的.

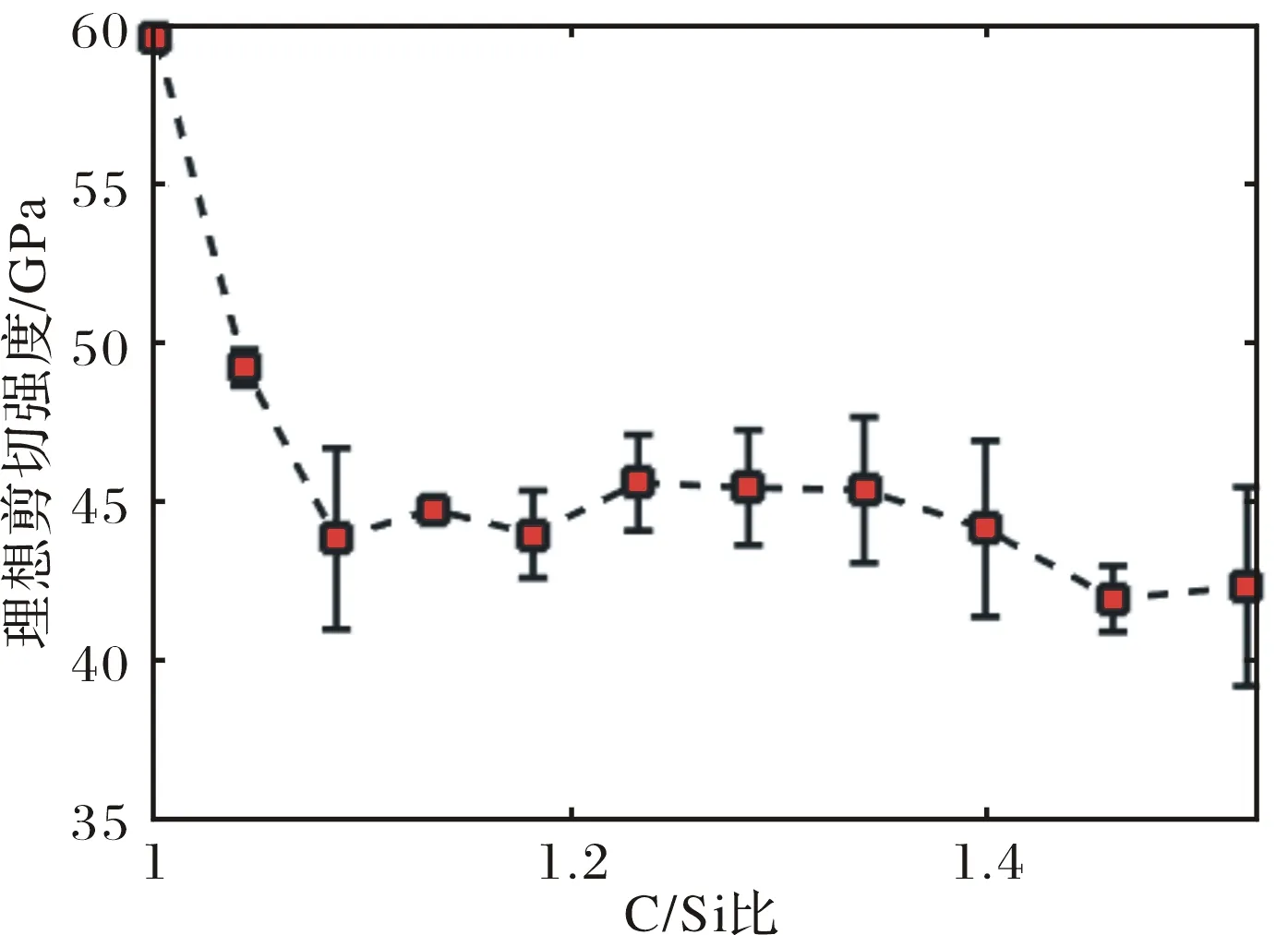
图3 SiC沿[100]方向理想剪切强度随C/Si比的变化曲线Fig.3 The ideal shear strength along [100] direction of SiC as a function of the C/Si ratio

3 结果分析

3.1 键长分析

固体SiC中，每个C原子周围是4个Si原子，每个Si原子周围是4个C原子.C原子一旦取代Si原子必然会形成至少5个C原子聚集的C团簇(见图1)，这个C团簇的结构与金刚石的结构相似.而金刚石中的C-C键键长为1.55Å，而SiC晶体中的Si-C键键长为1.89Å，前者比后者要短18%.图1所示的C/Si比为1.09的结构中，AD(C-C)原子之间的键长为1.66Å，CD(Si-C)原子之间的键长为1.93 Å.C原子取代Si原子之后，取代后C原子周围的键长均会发生变化，首先取代的C原子与周围的C原子形成了C-C键，C-C键比原来的Si-C短，C团簇进一步收缩，与C团簇相连的Si-C键在C团簇的收缩应力下被拉长.因此，经C原子取代后Si原子后的SiC中，C-C键要比金刚石中的C-C要长，而Si-C键也比晶体SiC中的Si-C键长，在C团簇周围形成了内部拉伸应力.这个内部应力会使SiC的机械性能降低，也使得结构在剪切过程中最先发生原子键断裂的地方出现在C团簇中被拉长的C-C键或者Si-C键.从能量的角度看，金刚石中C-C键的结合能能是8.55 eV[19]，而SiC中Si-C键的结合能则是2.35 eV[20]，也就是说，形成金刚石结构较形成SiC结构释放更多的热量.总之，SiC中C原子聚集成C团簇，导致SiC产生内应力，进一步导致SiC机械性能变差.

图4所示的是图1结构达到剪切强度后，原子键断裂后的结构.图中可以看出断裂的键均出现在2个取代的碳原子A原子和B原子周围，如AD键，还有未标记出的B原子周围的C-C键和Si-C键.这也证实了由于C团簇的出现形成了内应力，致使断裂的地方都出现在C团簇附近.

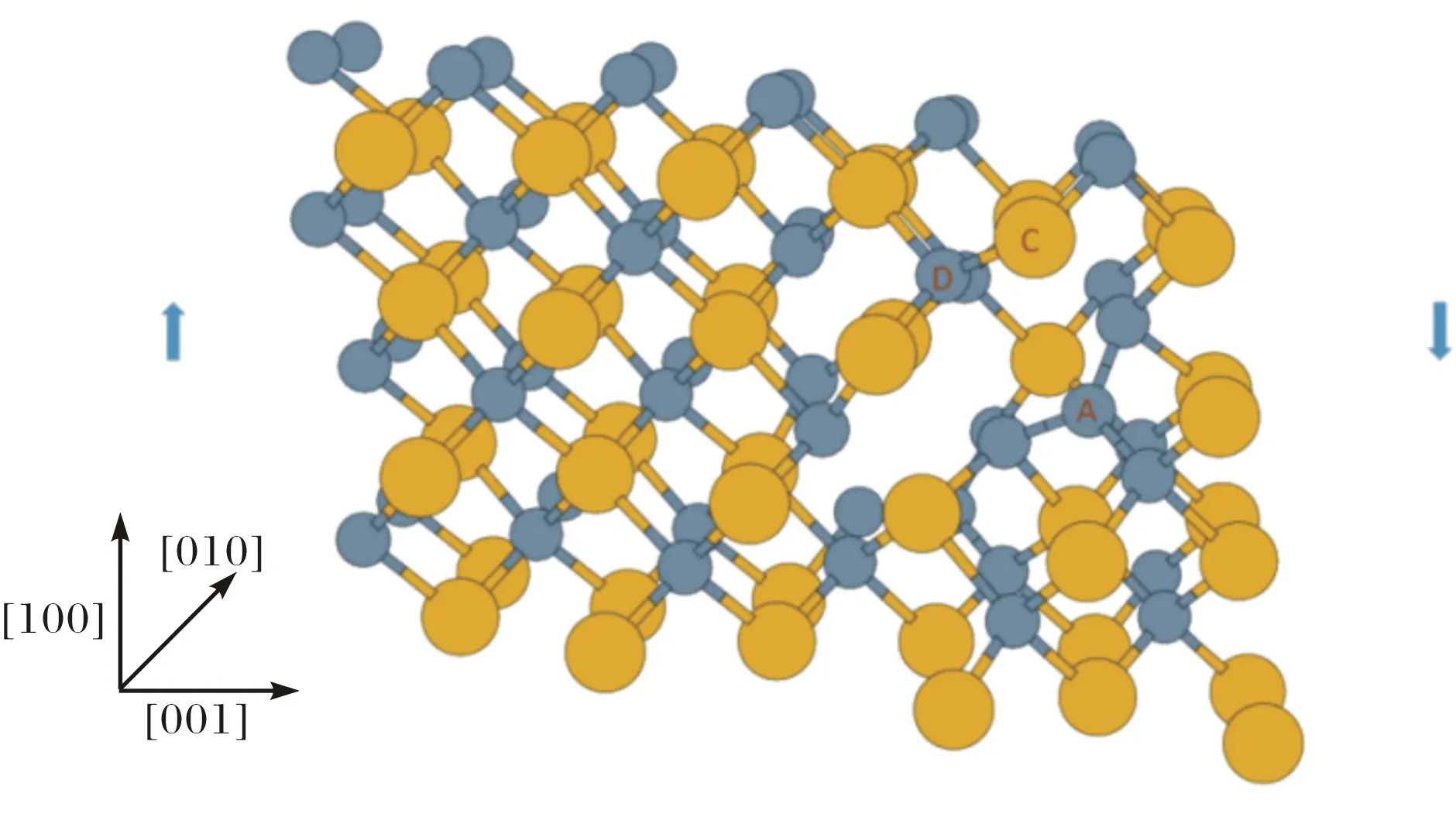
图4 C/Si比为1.09的SiC沿[100]方向上剪切后，原子键断裂后的结构Fig.4 The configuration of broken SiC sample with the C/Si ratio of 1.09

3.2 C团簇大小的影响

当2个以上C原子取代的Si原子比较靠近时，这时SiC晶体中就会形成较大的C团簇，C团簇的大小对理想剪切强度也有很大的影响.图3中同一C/Si比下不同结样品的理想强度偏差的出现，由于取代的C原子所在位置不同和C原子团簇的大小不同，导致5个计算样品结构不同，计算出的理想强度结果出现偏差.关于C团簇大小对理想强度的影响在文献[12]有更深入的讨论，由于理想强度的定义为原子键发生断裂所受的应力值，因此剪切与拉伸强度的本质一样，也是C团簇越大，则剪切强度下降的越多.

4 结论

本文用第一性原理的方法研究了C/Si比对SiC[100]方向上理想剪切强度的影响，从计算结果来看，随着C/Si比的增加，SiC在[100]方向上的理想剪切强度总体上是呈现下降趋势的.所选取的计算样品中，由于C原子取代Si原子在SiC内部集聚成C团簇，使得SiC在C团簇附近出现内应力.内应力的出现使SiC的理想剪切强度下降，并且在剪切作用下发生断裂的原子键均为受内应力影响的C-C键或者Si-C键.相比于均匀分布的C团簇，大的C团簇能进一步减少SiC的理想剪切强度.

[1] NEWSOME G, SNEAD L L, HINOKI T, et al. Evaluation of neutron irradiated silicon carbide and silicon carbide composites[J]. Journal of Nuclear Materials, 2007, 371(1-3): 76-89．

[2] KATOH Y, SNEAD L L, HENAGER J R, et al. Current status and recent research achievements in SiC/SiC composites[J]. Journal of Nuclear Materials, 2014, 455(1-3): 387-397．

[3] 于海蛟, 周新贵, 张 炜, 等. 聚变堆结构材料SiC/SiC的研究进展[J]. 材料导报, 2009(23): 104-108．

[4] HINOKI T, LARA-CURZIO E, SNEAD L L. Mechanical Properties of High Purity SiC Fiber-Reinforced CVI-SiC Matrix Composites[J]. Fusion Science and Technology, 2003, 44(1): 211-218．

[5] SNEAD L L, KATOH Y, KOHYAMA A, et al. Evaluation of neutron irradiated near-stoichiometric silicon carbide fiber composites[J]. Journal of Nuclear Materials, 2000, 283: 551-555．

[6] HINOKI T, KATOH Y, KOHYAMA A. Effect of Fiber Properties on Neutron Irradiated SiC/SiC Composites[J]. Materials Transactions, 2002, 43(4): 617-621．

[7] OZAWA K, NOZAWA T, KATOH Y, et al. Mechanical properties of advanced SiC/SiC composites after neutron irradiation[J]. Journal of Nuclear Materials, 2007, 367: 713-718．

[8] LI T, MORRIS J W, CHRZAN D C. Ideal tensile strength of B2 transition-metal aluminides[J]. Physical Review B, 2004, 70(5): 054107(1-5)．

[9] LAMBRECHT W R L, SEGALL B, METHFESSEL M, et al. Calculated elastic constants and deformation potentials of cubic SiC[J]. Physical Review B, 1991, 44(8): 3685-3694．

[10] LI W, WANG T. Elasticity, stability, and ideal strength of β-SiC in plane-wave-based ab initio calculations[J]. Physical Review B, 1999, 59(6): 3993-4001．

[11] UMENO Y, KUBO A, NAGAO S. Density functional theory calculation of ideal strength of SiC and GaN: Effect of multi-axial stress[J]. Computational Materials Science, 2015, 109: 105-110．

[12] LI Y, XIAO W. First principles study of the C/Si ratio effect on the ideal tensile strength of β-SiC[J]. Computational Materials Science, 2015, 110: 215-220．

[13] GAO F, BYLASKA E J, WEBER W J et al. Ab initio and empirical-potential studies of defect properties in 3C-SiC[J]. Physical Review B, 2001, 64(24): 245208(1-7)．

[14] ERHART P, ALBE K. Analytical potential for atomistic simulations of silicon, carbon, and silicon carbide[J]. Physical Review B, 2005, 71(3)：035211(1-14)．

[15] KRESSE G, HAFNER J. Ab initio molecular dynamics for liquid metals[J]. Physical Review B, 1993, 47(1): 558-561．

[16] KRESSE G, HAFNER J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium[J]. Physical Review B, 1994, 49(20): 14251-14269．

[17] KRESSE G, JOUBERT D. From ultrasoft pseudo-potentials to the projector augmented-wave method[J]. Physical Review B, 1999, 59(3): 1758-1775．

[18] GUO H, WANG B, JIA P, et al. In-plane shear behaviours of a 2D-SiC/SiC composite under various loading conditions[J]. Ceramics International, 2015, 41(9): 11562-11569．

[19] ZAVODINSKY V G. Ab initio simulation of diamond epitaxial growth on copper[J]. Computational Materials Science, 2006, 36(1-2): 139-142．

[20] AGRAWAL B K, YADAV P S, YADAV R K, et al. Ab initio theoretical study of SiC microclusters[J]. Progress in Crystal Growth and Characterization of Materials, 2006, 52(1-2): 15-20．

First-principles study of C/Si ratio effect on the ideal shear strength of SiC

SU Wen1， LI Yingying2

(1.School of Power and Mechanical Engineering， Wuhan University， Wuhan 430072；2.State Nuclear Power Research Institute， Beijing 100029)

The C/Si atom ratio effect on the ideal shear strength of SiC is investigated with first-principle calculation. The stoichiometric ideal β-SiC model is established. Then the Si atom of the model is replaced by C atom and Monte Carlo (MC) simulations are used to generate non-stoichiometric SiC samples. The C/Si atom ratio of which ranges from 1 to 1.52. Each non-stoichiometric SiC super cells is sheared along the [100] direction and the stress-strain relationship is obtained. The calculation results show that the ideal shear strength of the SiC decreases generally with increase of the C/Si atom ratio. Under the shear loading, the sample breaks at the Si-C bonds or the C-C bonds around the carbon cluster. The concentration of C atoms reduces the ideal shear strength because of the internal strain around the carbon clusters. Furthermore, the larger the size of carbon cluster is, the more dramatically the ideal shear strength reduces.

ideal shear strength； first-principle calculation； Monte Carlo simulation； SiC； carbon cluster； non-stoichiometric

2015-11-03.

1000-1190(2016)02-0196-06

O482.1

A

*E-mail: suwen@whu.edu.cn.