例谈高考中“参数范围”问题的求解策略

☉江苏省栟茶高级中学　陈德军

例谈高考中“参数范围”问题的求解策略

☉江苏省栟茶高级中学陈德军

在近几年的高考中，求参数的取值范围问题成了高考的热点，对于学生来说也是难点，求参变量的取值范围是高中数学中的一个重要内容，其中不少问题靠传统方法不容易求解，下面笔者结合一些教学实践谈谈其应用.

一、利用函数最值求参数的取值范围

解题中遇到形如“要使f（x）＞a成立”或“要使f（x）＜a成立”的问题，只需转化为求函数的最值，使得f（x）min＞a恒成立或f（x）max＜a恒成立即可.

案例1已知a＞0，b∈R，函数f（x）=4ax3-2bx-a+b.

（1）证明：当0≤x≤1时.

①函数f（x）的最大值为|2a-b|+a；

②f（x）+|2a-b|+a≥0.

（2）若-1≤f（x）≤1对x∈［0，1］恒成立，求a+b的取值范围.

解析：（1）①f′（x）=12ax2-2b=12a

当b≤0时，有f′（x）≥0，此时f（x）在［0，+∞）上单调递增.

所以当0≤x≤1时，f（x）max=max｛f（0），f（1）｝=max｛-a+ b，3a-b｝=

②由于0≤x≤1，故当b≤2a时，f（x）+|2a-b|+a=f（x）+ 3a-b=4ax3-2bx+2a≥4ax3-4ax+2a=2a（2x3-2x+1）.当b＞2a时，f（x）+|2a-b|+a=f（x）-a+b=4ax3+2b（1-x）-2a＞4ax3+4a（1-x）-2a=2a（2x3-2x+1）.

设g（x）=2x3-2x+1，0≤x≤1，则g′（x）=6x2-2=

x00，3（）3（）11 g′（x）-0+ g（x）1减极小值增13 333，

所以，当0≤x≤1时，2x3-2x+1＞0.

故f（x）+|2a-b|+a≥2a（2x3-2x+1）≥0.

（2）由①知，当0≤x≤1时，f（x）max=|2a-b|+a，所以|2a-b|+a≤1.

若|2a-b|+a≤1，则由②知f（x）≥-（|2a-b|+a）≥-1.

所以-1≤f（x）≤1对任意0≤x≤1恒成立的充要条件

在直角坐标系aOb中，上面的不等式组所表示的平面区域为如图1所示的阴影部分，其中不包括线段BC.

图1　

作一组平行线a+b=t（t∈R），得-1＜a+b≤3.

所以a+b的取值范围是（-1，3］.

特别地，注意条件“a＞0”，重视端点的取值情况.

二、利用分离参数求参数的取值范围

所谓分离参数，是指在含有参数的方程（不等式）中，通过同解变形，使参数与主元分离于方程（不等式）两端，则所蕴含的函数关系便由隐变显，进而研究函数的最大值（极值）或图像，求出参数范围.分参法是解决参数取值范围的常见解法，它的最大好处就是函数不再含有参数，变成了一个具体的函数，从而避免了讨论.

案例2f（x）=x-ln（x+a）（a＞0）的最小值为0.

（1）求a的值；

（2）若∀x∈［0，+∞），都有f（x）≤kx2成立，求k的最小值；

解析：（1）a=1.（过程略）

（2）x-ln（x+1）≤kx2，当x=0时，k∈R.

故φ（x）在（0，+∞）上单调递减，φ（0）=0，所以φ（x）＜0，即g′（x）＜0；

分参之后能得到具体的函数，不用讨论，但是得到函数后再求极值是一个难点，当一阶求导后，需要把分子单独拿出来研究其零点的情况，很多题在求导后是分式，需要进一步研究分子，不要在带着分母整个求导.

三、利用构造函数求参数的取值范围

解题中若遇到有关不等式、方程及最值之类问题，利用参数分离会失效，这时可以设法建立起目标函数，并确定变量的限制条件，用函数的观点加以分析，常可使问题变得简单明了，从而易于找到一种科学的解题途径.此类问题对转化能力要求很高，不能有效转化是解题难以突破的主要原因，要善于构造函数证明不等式，从而体现导数的工具性.

案例3设函数f（x）=ex-1-x-ax2.

（1）若a=0，求f（x）的单调区间；

（2）若x≥0时，f（x）≥0，求a的取值范围.

解析：（1）略.

（2）注意到f（0）=0，f′（x）=ex-1-2ax，由ex≥x+1，当且仅当x=0时等号成立，故f′（x）≥x-2ax=（1-2a）x，从而1-2a≥0.

当x∈（0，ln2a）时，φ′（x）＜0⇒φ（x）在（0，ln2a）上单调递减，φ（0）max=0，故x∈（0，ln2a）时，φ（x）＜0，即f′（x）＜0.

故x∈（0，ln2a）时，f（x）在（0，ln2a）上单调递减，f（0）=0.故x∈（0，ln2a）时，f（x）＜f（0）=0，故a＞1不成立. 2

此题若要用分参法解决，需要罗比达法则，超出了高中知识范围，故本题只能用讨论法去做，那么这类问题有什么共同的特点呢？注意题中的条件“若x≥0时，f（x）≥0”，当x=0正好有f（x）=0，这是讨论法的关键提示.

四、利用不等式放缩求参数的取值范围

要证明不等式A＜B成立，有时可以将它的一边放大或缩小，寻找一个中间量，如将A放大成C，即A＜C，后证C＜B，这种证法便称为放缩法，常用的放缩技巧有：（1）舍掉（或加进）一些项；（2）在分式中放大或缩小分子或分母；（3）应用基本不等式进行放缩.

案例4若函数h（x）满足：①h（0）=1，h（1）=0；②对任意a∈［0，1］，有h（h（a））=a；③在（0，1）上单调递减.则称h（x）为补函数.

（1）判断函数h（x）是否为补函数，并证明你的结论.

（2）若存在m∈［0，1］，使h（m）=m，称m是函数h（x）的中介元.记p=（n∈N*）时h（x）的中介元为xn，且Sn=若对任意的n∈N*，都有Sn＜12，求λ的取值范围.

（3）当λ=0，x∈（0，1）时，函数y=h（x）的图像总在直线y=1-x的上方，求p的取值范围.

解析：（1）函数h（x）是补函数.（证明略）

①当λ=0时，中介元xn=

（0，1）或

得中介元xn=

综合①②知，对任意的λ＞-1，中介元为xn=

于是，当λ＞-1时，有Sn=当n无限增大时，）n无限接近于0，Sn无限接近于

故对任意的n∈N*，Sn＜成立等价于

即λ∈［3，+∞）.

（3）当λ=0时，h（x）=（1-xp

②当p＞1时，依题意只需（1-xp）p＞1-x在x∈（0，1）时恒成立，也即xp+（1-x）p＜1在x∈（0，1）时恒成立.设φ（x）= xp+（1-x）p，x∈（0，1），则φ′（x）=p［xp-1-（1-x）p-1］.由φ′（x）= 0，得x=时，φ′（x）＜0，当时，φ′（x）＞0.又因为φ（0）=φ（1）=1，所以当x∈（0，1）时，φ（x）＜1恒成立.

综上可得p的取值范围是（1，+∞）.

本题考查导数的应用、函数的新定义，函数与不等式的综合应用，以及分类讨论、数形结合的数学思想.点（xp，h（xp））不在直线y=1-x的上方，不符合条件.

1

五、利用数形结合法求参数的取值范围

某些含参不等式恒成立问题，既不好分离参数求解，又不能转化为某个变量的一次或二次函数时，则可采用数形结合法.利用数形结合往往能迅速而简捷地找到解题途径.对于解含参不等式恒成立问题，我们可以先把不等式两端的式子分别看成两个函数，且画出两函数的图像，然后通过观察两图像的位置关系，从而列出关于含参不等式的约束条件，进而解决问题.

案例5已知函数f（x）=-x2+8x，g（x）=6lnx+m，是否存在实数m，使得y=f（x）的图像与y=g（x）的图像有且只有三个交点？若存在，求出m的取值范围；若不存在，说明理由.

解析：假设存在这样的实数m，满足题意，故可构造函数F（x）=f（x）-g（x）=-x2+8x-6lnx-m（x＞0）.

因为函数y=f（x）和函数y=g（x）的图像有且只有三个交点，所以也就是函数y=F（x）有三个不同的零点，即关于x的方程-x2+8x-6lnx-m=0有三个不同的实数根，于是再构造函数y=m，φ（x）=-x2+8x-6lnx，也即这两个函数图像有且只有三个交点.

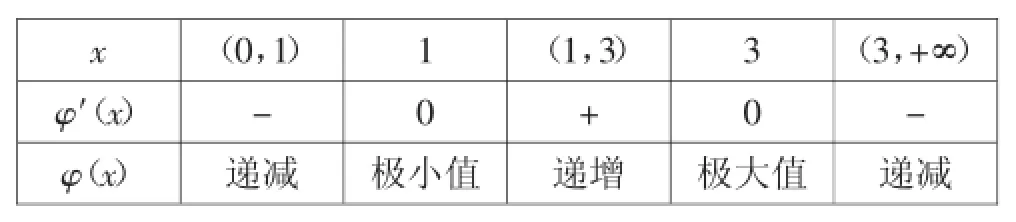
x（0，1）1（1，3）3（3，+∞）φ′（x）-0+0-φ（x）递减极小值递增极大值递减

图2　

由上表和图2可知，当直线y=m位于两极值点之间时，函数y=m和φ（x）=-x2+8x-6lnx的图像有且只有三个交点，即7＜m＜15-6ln3.

所以存在这样的实数m∈（7，15-6ln3），使得y=f（x）的图像与y=g（x）的图像有且只有三个交点.

数学家华罗庚说：“数缺形时少直观，形缺数时难入微.”通过移项，重组转化为常见的熟悉的函数（一次函数、二次函数、指数函数、对数函数、三角函数等），通过图像研究函数问题是具备较高数学素养的表现之一.

由此可见，求参数取值范围问题一直是高考的重点、热点，也是一个难点，一些含参变量的问题，往往看起来很复杂，甚至无从下手.但如果能把握题目的结构，通晓基本题型的解法，进而确定求解方法，则会收到简捷明了、事半功倍的效果.F