问题引领教学让学生既懂又会

☉安徽省寿县第一中学　梁昌金

问题引领教学让学生既懂又会

☉安徽省寿县第一中学梁昌金

一、引言

“懂而不会”是学生学习数学过程中经常出现的现象，也是一种正常现象，可以说数学的复杂性就在于“懂”不代表“会”.“懂”指知道、了解，“会”指理解、领悟，可见“懂”与“会”是学习过程中的两个不同阶段、不同层次、不同境界.一种解题方法学生听得懂与自己会用此方法解决问题不是一回事.“懂”方法是对别人解题方法的理解，“会”方法是自己能想到解法，并能解决问题，学生要把听得懂的知识转化成为自己应用、掌握的知识，把自己掌握的知识转化为自己会应用的知识，其中还有一段很长的“距离”.这段距离可以说是学生学习的关键过程，也是教师无法替代的过程.教师在平时教学中由于对此认识不清，错误理解“懂”与“会”的关系，误认为“懂”就代表“会”，教学应该多停留在把学生教“懂”的层面，如课堂反复问学生懂不懂，让学生懂是教师教学的基本要求，如果一堂课下来学生连“懂”都“不懂”，那是教师教学的最大失败.除此，教师还要创造条件重视过程教学，让学生学习既懂也会，由懂到会，会了更懂，“会”才是师生教学与学习追求的目标.“会”是知识内化到认知结构的表现，“会”是学生建构了“自己的理解”，“会”是能力形成的体现.本文以笔者所在学校两位教师在高三一轮复习时对一道高考题的教学为例，简单谈谈自己的认识与理解.

二、教学过程简介

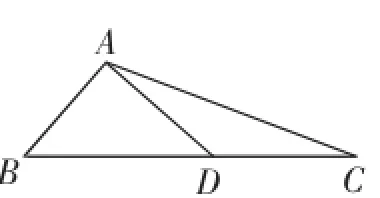
图1　

（一）甲教师课堂教学

生1：可以建立平面直角坐标系求解.

师：说说你的解法.

生1：如图2，以点A为坐标原点，AB所在直线为x轴建立平面直角坐标系，则由已知条件得D（0，1），设AB= a，因为所以点C的坐标为

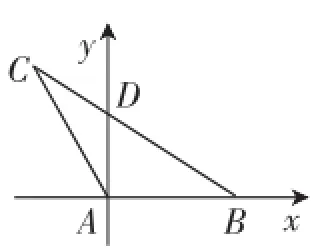
图2　

师：很好，此类问题一般建立坐标系都可以求解，解题时要注意建系的方法，要有利于相关点坐标的求解，还有其他方法吗？可以对所求量进行分解转化吗？

教师：说一说你的求法.

生2：因为

师：非常好，只要选择好基底把所求向量转化到基底向量上就可以了，其他同学是不是都会了？（得到学生肯定后）下面看一道题.

……

甲教师借助学生重点讲授两种“已会”的解题方法，整个过程无论是建系、设点、用坐标法，还是直接选择向量基底表示向量，在教师引导下，学生都能顺利解决问题，听得“懂”，问题是学生“会”吗？面对新问题，两种方法到底选择哪一种较好？两种方法有何不同？是不是所有的数量积问题都能用这两种方法解决？为什么不直接使用向量数量积公式？这两名学生会了，其他学生会吗？其他学生还有什么样的理解？这些问题不解决，学生遇到简单题可以模仿解决，但是遇到稍微复杂一点的题目可能就没有办法，或不能在短时间内迅速解决了，因为学生在解题的过程中没有学会“解题”，没有学会分析问题，探寻思路的方法.

（二）乙教师课堂教学

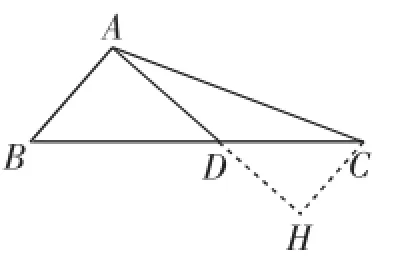
图3　

师：分析得很好，拿到问题首先思考公式能否使用，学生1从公式使用出发，立足于公式结构特点，层层分解任务，逐步逼近目标，最终把问题转化为求线段AH的长，谁能求出AH的长？

（太繁了，学生有畏难情绪）

师：很好，虽然繁了点，但是可以解答出来，同学们

师：很好，构造直角三角形，通过借助平面几何知识，利用三角形相似，联系已知与未知，顺利解决问题，这也是解决此类问题常用的方法，别忘记相得益彰，有利于对问题迅速、巧妙地解决，学习中遇到例子多体会，请大家思考，还有其他的方法吗？还可以怎样解决？不作辅助线是否可以？

师：（学生思考一会，教师提问学生）请生3说说.

生3：没想好，不作辅助线不会表示|A—→C|cosθ.

师：生4呢？

生4：若不作辅助线，选择一个量，可以是边或角，只要能表示出cosθ和AC即可，但表示cosθ有困难.

师：很好，这也是我们考虑问题的一般方法，哪个角含θ？我们目标是使用条件，既要含角θ，也要与已知条件相联系，最好是直接联系，能一步到位最好.

生5：由于θ是△ADB的内对角，∠ADB=∠ACD+θ，而cos∠ADB=，即AC·做一做，同时考虑能否优化思路，减少思维回路.

师：漂亮！应用正弦定理，直接将已知与未知联系起来，直达目的，简洁明快，但要认识到sin（90°+θ）就是cosθ很关键，所以知识要放在联系中理解，在理解问题中使用，生5表示条件没有生6直接，所以繁了点.

师：以上两位同学围绕向量数量积公式的使用，从两个不同角度进行求解，相似、正弦定理都用上了，很精彩，请思考还有其他的处理方法吗？

师：可以，选择哪两个向量作为基底？标准是什么？所求向量是否都能转化到已选择基底向量上.

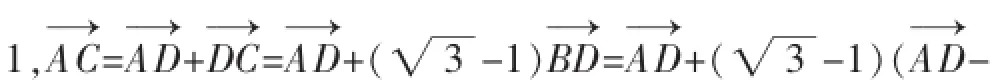
师：也很容易，选择基底为什么能解决问题呢？此法能否成为通性通法？

生7：可以作为解决此类问题的通法，但要知道“已知基底”，因为平面上任何一个向量都可以通过给定基底来表示，若此基底的夹角与模已知，当然其他向量间的关系可以通过选择基底解决.

师：解释得很好，其他同学理解了吗？考虑还有其他解难法吗？

生8：建系.

师：如何建？

生8：抓住AD⊥AB，建立如图2所示的直角坐标系，设AB=a，则D（0，1），又因为

师：很好，用坐标法也很简捷，问题是对新问题何时选择“基底”法？何时用建立坐标系法？两种方法是否有相通之处？

生9：应是不同方法，当有已知的特殊角时建系方便.（其他学生也认同）

师：坐标的方法是怎么来的？是否是以互相垂直的单位向量作为基底的？（至此学生才恍然大悟）其实选择“基底”是更一般的方法，只是有了坐标以后运算更方便罢了，本题还可以怎么解？

师：（学生没回答）设AB=a有作用吗？结果有a吗？

生10：可以特殊化，设AB=1.

师：可以，还有更简单的吗？

生11：既然与AB的长没有关系，直接令AB=0最简单，此时AC=BC=

师：请做下面的练习.

……

乙教师很好地体现了以教师为引导、学生是学习主体的教学理念，层层设问，步步启发，虽然浪费了更多的时间，但通过有效的问题引导，把解决问题的方法变成了学生“自己的方法”，把学生解题过程变成了“再创造”过程，使学生学会选择，真正做到了由“懂”到“会”.

三、让学生建构自己的理解

（一）创设学生自主发展的学习环境

高中数学由于内容多、难度大、时间紧，无论是新授课还是高三复习课，讲都讲不完，所以现实的教学情况是课堂教学上教师多采用直接讲授法，保证完成教学任务.即使在新课标实施后，教师教学理念有变化，但常规教学状况也没有多大改观，与此相反的结果是，学生掌握得越少.很明显学习效果主要取决于学生学的情况，这就要求教师在平时教学中改变学生被动听、懂而不会的情况，多创造学生自主发展的学的活动环境，促进学生自主学习、主动学习、主动理解、主动建构、主动应用、主动创造、主动发展，如果教师认为“没有教过的东西学生不可能会”，那么，学生很快也就会放弃独立思考的习惯，并认为“没有学过的东西我们当然不会”.所以教师要转变观念，信任学生，信任学生的学习潜能，解放学生思想，给学生自主学习的时间、空间和机会.上例教学中两位教师都没有直接讲解题方法，由学生自主提出解决方法，给学生充分发展、交流的机会.当然学生自主发展不是自由发展，其自主离不开教师的引领、引导、帮助、设计、规划和激励，学生要主动预习、主动思考、主动建构，思维要走在教师的前头，改变被动学习的局面，学会主动发展、主动迎接挑战、主动由懂达会.

（二）创设学生建构“自己的理解”的学习过程

建构主义的核心观点就在于：学习并非是学生对教师所授知识的被动接受，而是一个以其已有知识和经验为基础的主动建构过程.另一方面，由于任何活动都是主体的主动建构，因此，即使就同一数学内容的学习，不同的个体也完全可能由于知识背景和思维方法等差异而具有不同的思维过程，因此学习过程是学生个性理解的过程，尽管外在的知识结构具有严密的逻辑性、完备性和结构性，但是，人们在理解这些知识结构时会根据个人的建构做出不同的解释，形成不同的表征系统，概念、公式等学习中要让学生体会其中的关键词，说出自己的理解，甚至自已举出相关例子来反映自己的理解，学生举例是检测学生是否理解的一种有效方法.平时教学要把概念的形成过程变成学生学习探究的过程，如学习平面向量的有关概念时，学生要明确为了向量“运算”学习零向量、单位向量、相等向量是必要的，而不是教师一味自己介绍概念，解题教学更要让学生感知从无到有的思维过程和将知识综合应用的整合过程，应将掌握知识变成会应用知识.案例教学中从乙教师的教学过程可以看出，学生思考问题是充满个性化的，面对同一问题都有自已的理解，都有自己的思考视角：有的从公式出发，有的从选择基底入手，有的从建坐标系开始，有的从特殊化切入，只有学生对概念、法则、公式等形成自己的理解，才能灵活运用，由懂到会.

（三）创设暴露解决问题的分析过程

平时学习与高考不是一回事，高考要求学生用最简捷的方法在最短时间内解决问题，赢得高考，而平时学习过程恰好相反，快速解题不是目的，借助解题学会分析问题、灵活应用知识形成解决新问题的能力是关键.因此，平时要舍得花时间对问题进行深入挖掘，多角度思考，纵横联系，充分暴露问题的思维过程，促进学生由懂到会，要真正“研究”解题.甲教师只让学生运用两种方法解题，且没有对方法进行解释，很多学生只处于“懂”的状态，只感知到方法可行，未必真正理解方法，更不能保证自己能运用方法，所以不会.课后了解，甲教师的观点是这两种方法最简单，直接使用公式有点繁，学生能够正确解答就行了，并没有对此进行深入挖掘，解题变成了目的，而乙教师立足对学生能力的培养，不仅要学生“懂”方法，更注重学生“会”方法.首先启发学生从公式出发，联系平面几何知识，体现知识的联系性；再引导学生思考，在尝试中调整思路，揭示两种方法本质的一致性，使学生学会选择，真正做到“会”用；特殊化方法的进一步使用，是对定值本质的揭示，更是对问题深刻的认识，简单题发挥了不简单的功能.学生经历这样的学习过程，有对问题的独立思考，有学生之间的相互交流与启发，有教师的合理引导，使学生思维得到深度参与，怎能不会！

（四）创设方法层面引导的学习过程

学生高效学习离不开教师引导，自主发展不是乱发展，“自己的理解”是在有效的学习环境下建构的，也离不开教师的启迪.课堂教学教师给予方法论层面的引导是帮助学生建构“自己的理解”的关键，乙教师估计到学生可能会直接用建系的方法求解，所以首先引导学生“如何直接使用向量数量积公式a·b=|a||b|cosθ”，拿到问题首先考虑现有的概念、公式等能否直接使用，从最根本的通性通法思考，而不是总是找“方法”.在学生作出辅助线解决问题后，教师没有止步，继续启发学生“还有其他的思考方法吗？还可以怎样解决？不作辅助线是否可以？”“我们的目标是使用的条件既要含θ角，又要与已知条件相联系，最好是直接联系，能一步到位最好.”“逼”学生在思维的调整过程中想出正弦定理.在学生用选择基底法与本质有何不同，从而总结出选择基底才是更一般的方法，才是通性通法，使学生的认识得到升华，理解得更深刻.在学生没有想到“高效”的特殊化方法后，教师反问“设AB=a，有作用吗？结果有a吗？”学生在教师的启发下自然想到“特殊化”方法，更是在特殊化追寻得到问题的本质是定值，所有的方法教师都没有直接“告知”，而是通过有效的方法论层面问题引导，把解决问题的方法变成学生“自己的方法”，把学生过程变成“再创造”过程.在创造过程中学生形成自己的方法，当然会了.

（五）创设高效练习过程促进学生迁移能力提升

迁移是问题解决核心，能迁移也是学生“会”的表现.练习是实战，是应用知识，是把陈述性知识转化为程序性知识的有效方法.因此，练习可以促进学生迁移能力的提升，促进学生综合能力的发展，由懂转会，学生先做模仿性练习是必要的，迁移从模仿开始，在练习中再进一步感悟方法、理解概念、体会思想.所以学习数学要注重学生练习，但练习要在解题方法的形成上要让学生充分感悟方法的自然性.在比较中使用方法，特别要增强变式教学；在变化中使用方法，变模仿为创造，而不是一道接一道地做题.

1.王弟成.启发他，而不是告知他［J］.中学数学教学参考（上），2015（4）.

2.程坚.用理论指导解题教学消除“懂而不会”现象［J］.数学通讯（下），2015（5）.

3.蒋大春.从教的视角看解题过程中的“懂而不会”现象［J］.中学数学研究（南昌），2014（7）.Y