“用二分法求方程的近似解”的教学设计与反思

☉甘肃省陇西县第一中学　杨瑞堂

“用二分法求方程的近似解”的教学设计与反思

☉甘肃省陇西县第一中学杨瑞堂

本节课是以“问题驱动式”和“启发探究式”为主，情景陶冶、示范模仿、讨论、自主探究、协作学习相结合的建构主义学习过程.

一、教材分析

“用二分法求方程的近似解”是普通高中新课程标准实验教科书《数学必修1》（人教A版）第三章“函数的应用”中第一节“函数与方程”的第二部分，属于数学方法范畴，是一节新授课.本节课是在学习了“方程的根与函数的零点”的基础上引入的，主要任务是探究二分法的基本思想方法，体会逼近思想，根据具体函数的图像，能够借助计算器用二分法求给定精确度的方程的近似解，了解这种方法是求方程近似解的基本方法，并在总结“用二分法求函数零点的步骤”中渗透算法思想，为学生后续学习算法做铺垫.

二、学情分析

本节课的教学对象是普通高中高一年级学生，学生的数学基本功相对比较扎实，思维活跃，数学学习兴趣较为浓厚.在本节课之前，学生已经学习了方程的根与函数零点，能够理解函数的零点、方程的根、函数图像与x轴交点的横坐标之间的等价关系，有一定的等价转化和数形结合思想，比较熟悉一元二次方程的根与一元二次函数的零点，对于高次方程和超越方程比较陌生，将其方程的根转化为函数的零点有一定的困难；但对于具体情境的探究，能够及时积极参与其中，小组合作意识较强，为寻求解决方案提供保障.

三、学习目标

通过实例理解二分法的基本思想方法，根据函数的图像，能够借助计算器用二分法求相应方程的近似解，了解二分法是求方程近似解的一种方法，从中体会函数与方程之间的联系，以及逼近、程序化解决问题的思想；通过数学实验情境的探究，激发学生的学习兴趣和热情；通过合作探究、讨论交流、作业展示，养成良好的学习习惯，增强合作意识，提高数学语言表达能力和沟通能力，在潜移默化中，体会数学解题的魅力，增加学习兴趣.

四、重点与难点

用数学实验情境的探究，激发兴趣，实现对二分法原理的探究，以突破学习难点；通过示范模仿，具体联系，学会用二分法求方程的近似解，掌握重点.

1.学习重点

二分法原理及其探究过程，用二分法求方程的近似解.

2.学习难点

对二分法原理的探究，对精确度、近似值的理解.

五、教学过程

1.提出问题，引入新课

师：你会求下列方程的根吗？请先自主尝试.

（1）2x－6=0；（2）2x2－3x+1=0；（3）lnx+2x－6=0.

生：绝大多数学生自主完成了方程（1）、（2）的求解，但在求解方程（3）时犯难了.

设计意图：从学生熟悉的解方程引入，（1）、（2）是学生熟知的一元一次方程和一元二次方程，但面对（3）这种超越方程的根，并没有现成的求根公式，自然地引起学生的认知冲突，激发学习热情.

师：有很多方程用我们常规的公式法是很难求根的，比如高次代数方程、超越方程，所以研究方程的近似解非常必要.若问题变为“求方程lnx+2x－6=0的近似解”，你有什么想法呢？想一想，我们上节课学了什么呢？同桌之间可以相互讨论、叙述.

生：学生之间开始相互讨论、叙述方程的根、函数零点的概念及二者之间的等价关系.

师：求方程lnx+2x－6=0的近似解问题可以转化为？

生：求函数y=lnx+2x－6的零点的近似值.

师：通过上节课的学习，我们已经知道函数y=lnx+ 2x－6在区间（2，3）内有零点，那么如何找到零点呢？

设计意图：教师引导学生思考回顾方程的根与函数的零点的概念及关系，将求方程根的近似解的问题转化为找到函数零点，进一步体验等价转化思想.

2.创设情境，探究新知

情境探究，模拟实验室.

师：如图1，16枚金币中有一枚较轻，是假币，现在有一台天平，如图2，如何找到那枚假币呢？（先独立思考，然后和你的小组成员一起探讨吧）

图1　

图2　

生：先独立思考，然后和小组成员讨论；小组成员分享结果，其他同学聆听思考.（先分成8枚和8枚，称一下；再将较轻的8枚分成4枚和4枚，称一下；然后将较轻的4枚分成2枚和2枚，称一下；最后将较轻的2枚，称一下，较轻的1枚就是那枚假币）

设计意图：通过具体情境的探究，激发学生的学习兴趣，在实际问题的解决中体会逼近思想，体验一分为二的方法.

师：回想一下，我们是怎么找到假币的？此问题的解决对我们有何启发呢？和你的小伙伴讨论一下，并将想法分享给大家！（利用电子白板演示动态过程，如图3，教师观察，聆听）

图3　

生：小组讨论，将假币所在范围逐渐缩小，每次都是一分为二.

设计意图：小组成员相互讨论交流，不仅可以完善解决措施，而且相互叙说，可以促进逼近思想和二分法的内化.

师：通过这个小实验，你能想到什么样的方法求函数y=lnx+2x－6在区间（2，3）内的零点的近似解？

生：缩小区间，逐渐逼近.

师：如何缩小区间呢？

生：不断地一分为二.

师：如何将区间（2，3）一分为二呢？

生：取中点，可以得到（2，2.5）和（2.5，3）.

师：思考一下，哪个区间是我们需要的呢？该如何确定呢？（教师适当引导学生回忆零点存在性定理）

生：判断f（2）·f（2.5）与f（2.5）·f（3）的符号.

师：（引导学生共同探究，板书思维过程）因为f（2）＜0，f（2.5）＜0，f（3）＞0，所以零点所在区间是（2.5，3）.为了找到零点，我们还得继续将零点进行缩小.现在，请拿出计算器和你的四人小组一起，继续完成下表.

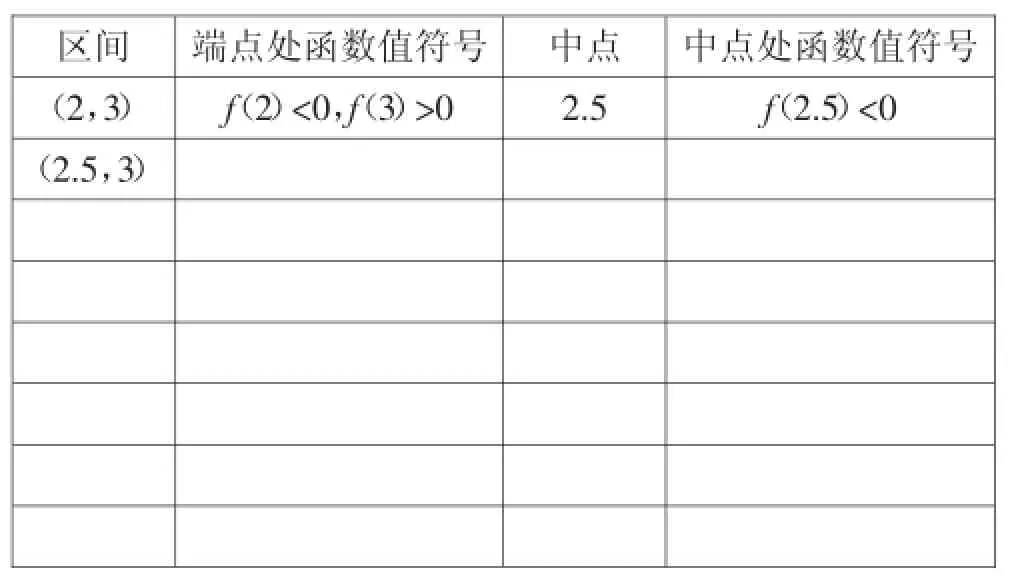
区间端点处函数值符号中点中点处函数值符号（2，3）f（2）＜0，f（3）＞02.5f（2.5）＜0（2.5，3）

生：小组合作，完成表格.

设计意图：教师引导学生，用二分法的思想不断地缩小零点所在的区间，然后让学生小组合作利用计算器，进行实践，为总结出二分法的步骤奠定基础.

师：一直算下去吗？你能给出一个停下来的标准吗？想一想，我们之前求近似值时，经常会有什么要求呢？

生：思考讨论，得到精确到小数点后几位.

设计意图：引出精确度的概念.

师：对于精确度ε的界定是：只要精确值所在区间的长度小于ε，那么这个区间内的所有值就都是满足精确度ε的近似值.在上述问题中，若精确度为0.01，请求出相应零点的近似值.

生：当a=2.53125，b=2.5390625时，|a－b|=0.0078125＜0.01，则该区间的任意一个值，都是x0的近似值.

师：为了方便，这里统一取区间端点a（或b）作为零点的近似值.

设计意图：让学生对精确度的概念更加清晰，明确如何根据精确度停止运算，找到零点的近似解.

师：这种将零点所在区间不断地一分为二，逐渐逼近函数零点的方法，就是我们今天的研究对象，用二分法求方程的近似解，请同学们打开课本P90页，阅读二分法定义.

生：自行阅读定义.

设计意图：引出二分法定义.

3.合作探究，深化理解

师：思考下面几个问题，并与你的同伴进行讨论交流.

（1）求函数f（x）的零点近似值第一步应做什么？

（2）为了缩小零点所在区间的范围，接下来应做什么？

（3）若f（c）=0，说明什么？若f（a）·f（c）＜0或f（c）·f（b）＜0，则分别说明什么？

（4）若给定精确度ε，如何选取近似值？

生：小组为单位，思考讨论交流，回答思考的问题.

设计意图：4个思考题引导学生进一步梳理二分法的实质和具体步骤.

师：试一试，用自己的话叙述用二分法求方程近似解的步骤，同桌之间，相互叙述一下.

生：同桌之间相互总结叙述用二分法求方程的近似解的步骤.

设计意图：用自然语言表述二分法求方程近似解的步骤，有利于学生将知识进行内化；同桌之间相互叙述，可以增强合作学习的意识，有利于学生达到不仅会做，而且会讲，进而让思维更清晰.

4.牛刀小试，巩固新知

师：小组合作，完成下列练习.

借助计算器，用二分法求x2=3在区间（－2，－1）内的近似解（精确度为0.1）.

生：小组成员，合作完成练习.

设计意图：通过练习，进一步巩固二分法的思想，明确用二分法求方程的近似解的过程.

5.归纳小结，巩固升华

师：请同学们思考、交流一下，这节课学到了什么？

生：自己思考，回想总结这节课的知识点和思想方法.

设计意图：学生自己总结，有利于巩固深化所学知识和思想方法.

6.作业布置，迁移深化

A：课本P92习题3.1A组第1，2，4题；

B：课本P93习题3.1B组第2，3题.

课外作业：除了二分法，你还知道哪些分割方法呢？搜集资料，整理成小论文，和大家一起探讨吧！

设计意图：作业分层设计，可以更好地适合不同学生的需求，以达到因材施教；课外作业有利于拓宽学生的数学视野，了解数学文化，感受数学魅力.

六、课堂教学评价设计

本节课的教学评价，采取观察法、访谈法、作业与测验相结合，从学生间互评、教师评价、学生自评三方面进行；评价内容为课堂表现评价、学习效果评价（课堂学习效果评价+作业）、小组合作评价.

观察法：教师在课堂教学过程中，通过问题的提出，情境的引入，观察学生的反应；在学生小组合作、思考讨论时，观察每个小组成员的表现.

访谈法：在课后，以个别访谈方式进行，就不同层次的男、女同学，个别访谈，询问课堂听课效率，以及存在的问题，进行学生之间的互评.

作业和测验：通过课后作业的批改，测验的成绩，阶段性地检验学生的学习效果，找到存在的问题，共性问题一起解决，个性问题单独处理，重点问题分享处理.

七、教学反思

“用二分法求方程的近似解”是函数与方程的第二节内容，属于数学方法范畴.教学设计初衷是以问题驱动和启发探究为主，通过提出问题，引入新课；创设情境，探究新知；合作探究，深化理解；牛刀小试，巩固新知；归纳小结，巩固升华；作业布置，迁移深化，这六步来完成教学内容，达到教学目标.经过教学实践发现，这种设计基本符合学生认知需求，内容衔接比较紧凑，但是仍有许多不足之处.

（1）问题引入过快，教师的提示语太多，基本上代替了学生，将问题进行转化，这样一来不利于学生建构知识体系.例如，在本节课的开头，以学生熟悉的一元一次、一元二次方程求根问题，引出了超越方程lnx+2x－6= 0，接下来应该留给学生自主探究的时间，让他们自己将方程的根与函数的零点进行等价转化，会更有利于学生体会和学会用函数思想解决问题.

（2）从具体情境中感受、归纳出二分法的基本思想到找出函数的零点，过渡太快，提示语控制性太强，限制了学生的自主探究能力，不利于学生将知识内化.如果将原本的提示语，通过这个小实验，你能想到什么样的方法求函数y=lnx+2x－6在区间（2，3）内的零点的近似解”，改为“这个小实验，对你有何启发”，给学生时间和空间，自发地联系二者之间的关系，可能会更好地掌握本节课的核心思想方法，同时解放了教师，更好地发挥学生的主体性.

（3）练习题的题目欠妥当，通过观察学生的课堂练习情况，发现部分学生对用二分法求方程x2=3在区间（－2，－1）上近似解的问题，不能及时地转化为求函数y= x2－3的零点问题，反而研究函数y=x2.课后反思，如果将题目改为对用二分法求方程x2－3=0在区间（－2，－1）上的近似解，这样会更符合学生的最近发展区，能够更好地学以致用，加深理解.

数学是一门语言，它也有听、说、读、写.在教学实践中，不仅让学生听得懂数学思想方法、感受到数学思维的奥妙，还能说得出、读得懂、写明白所思所想，让数学课堂变得像诗一样优美，充满活力，任重而道远，仍需努力探索.

1.人民教育出版社中学数学课程教材研究中心.普通高中课程标准实验教科书数学（必修1）［M］.北京：人民教育出版社，2007.

2.人民教育出版社中学数学课程教材研究中心.普通高中课程标准实验教科书数学（必修1教师用书）［M］.北京：人民教育出版社，2007.F