基于三维实体有限元模型的谐波齿轮装配状态应力分析

陈晓霞，程 凯

（1.天津工业大学机械工程学院，天津 300387；2.天津工业大学天津市现代机电装备技术重点实验室，天津300387）

基于三维实体有限元模型的谐波齿轮装配状态应力分析

陈晓霞1，2，程 凯1

（1.天津工业大学机械工程学院，天津 300387；2.天津工业大学天津市现代机电装备技术重点实验室，天津300387）

为准确地反映谐波柔轮的齿廓及齿根的应力状态，提出了基于真实齿廓信息的柔轮三维实体的建模方法.以渐开线齿形为例，利用APDL语言建立包括渐开线齿廓、齿厚和齿根倒圆等参数的实体模型.定义波发生器与柔轮筒内表面间接触，求解获得波发生器作用下的柔轮应力，与基于圆环理论的理论值比较分析；为更真实反映柔轮在装配状态下的应力分布，构建柔轮三维实体模型，求解柔轮应力.通过路径定义，提取与理论计算截面相对应的中截面上的应力，与平面齿圈的有限元结果和理论值比较分析.研究发现：平面齿圈有限元实体模型中，沿周向应力波动均值与理论值基本吻合，验证了文中的有限元实体建模方法的有效性.三维实体模型周向应力比平面齿圈周向应力大，且最大周向应力发生在顶层.

谐波齿轮；柔轮；有限元分析；三维实体模型；装配状态

谐波齿轮传动是基于柔轮的弹性变形来传递运动的.谐波齿轮的工作寿命主要取决于柔轮的工作寿命，因此柔轮的强度研究是谐波齿轮传动中的重要课题，而确定柔轮中的应力大小和分布规律是强度研究的关键［1］.

目前，许多研究者基于实体有限元模型来研究柔轮的应力和变形［2-3］.在使用ANSYS过程中，为了计算方便，研究者们都采用了不同的简化方法［4-5］.王知行等［6］把柔轮的轮齿均匀地抹平，看作光滑变厚度的薄壁壳；韩建华等［7］把齿圈视作当量厚度的光壳，分析了二点式波发生器作用下柔轮的应力分布规律，得出了柔轮结构参数对应力分布的影响和柔轮发生疲劳破坏的可能截面；Chen等［8-9］用壳单元和梁单元相结合的柔轮有限元模型计算双圆盘波发生器作用下柔轮变形和应力，得到齿圈部位的中性层、齿根、齿尖处的变形；付军峰等［10］建立了谐波齿轮传动中杯形柔轮与波发生器接触分析的有限元模型，得到了柔轮壳体空载时的应力分布状况.

刘文芝等［11］在啮合齿对接触边界的节点之间建立面-面接触单元，用三维弹性接触问题有限元法较全面地计算和分析了承载柔轮齿圈和筒体的应力和分布规律、轮齿变形及影响机理；吴伟国等［12］在ANSYS中建立带有整圈轮齿的刚轮和柔轮模型，利用其接触分析要素在啮合齿面间定义面-面接触对，使得各对轮齿在啮合时产生作用力，从而提出了一种与实际较接近的谐波传动有限元模型建模方法；董慧敏等［13-15］将柔轮轮齿简化为等厚度的壳体，用经验公式和实验结果计算得到了柔轮在不同负载条件下齿圈中面不同截面上的变形情况.

本文针对现有谐波传动有限元分析模型不够精细这一问题，利用APDL语言建立包括柔轮齿厚、齿根倒圆半径和齿槽壁厚等参数的参数化实体模型，并结合柔轮的渐开线方程，参数化设计了柔轮的渐开线齿廓，生成平面齿圈，添加平面波发生器.在平面齿圈径向上定义顶层、中层、底层3个路径.定义波发生器与柔轮筒内表面之间为线-线接触，求解获得波发生器作用下的柔轮应力，与基于圆环理论的理论值和设计规范值比较分析.将平面齿圈和波发生器轴向拉伸，再添加柔轮筒，生成柔轮的三维模型.在柔轮三维实体模型径向上定义顶层、中层、底层3个路径，轴向上定义前截面、中截面、后截面3个路径.定义波发生器与柔轮筒内表面之间为面-面接触，求解获得波发生器作用下的柔轮应力.提取三维模型中截面上不同层面上的应力与平面齿圈相应层上的有限元值、理论值和设计规范值进行比较分析.

1 装配状态下的应力计算

1.1 基于等效圆环理论的应力计算

本次研究采用四滚轮波发生器，以杯形谐波齿轮为例，刚轮和柔轮均采用变位的渐开线齿形.

按照圆环理论，考虑柔轮筒对齿圈的加强作用，建立具有等效刚度的等效圆环模型.利用等效圆环模型可以得到空载传动状态的圆环变形和应力计算公式，为啮合分析和应力强度计算提供依据.通过理论计算可以得到柔轮任意截面上的周向应力［16］：

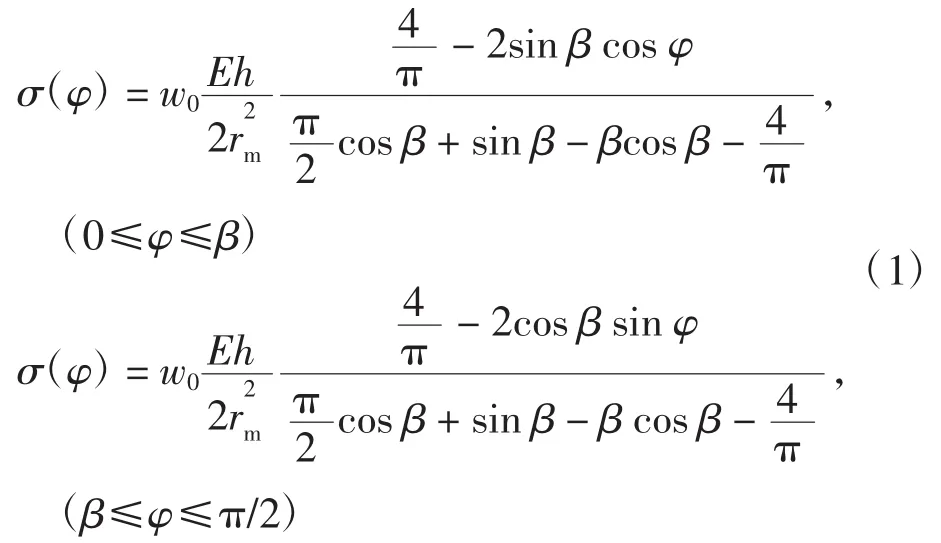
式中：φ为波发生器长轴相对柔轮未变形端的转角；β为滚轮安装轴的偏置角度；w0为最大径向变形量；E为材料的弹性模量；h为圆环的厚度，h=1.671/3s［10］，s为柔轮齿圈处的壁厚；rm为变形前柔轮中性圆曲线的半径.

1.2 设计规范中的应力计算

在设计规范中，为了简化强度计算，通常把柔轮简化为一个光滑圆柱壳体进行应力分析，然后再根据试验结果进行适当的修正.可求得，柔轮的周向应力最大值为［17］

式中：Krt为柔轮弯曲刚度引起的应力增大系数，设s*= s/m，Krt=（1+s*）/s*；KM为受载柔轮畸变引起的应力增大系数；Kd为动载荷系数；Cσ为正应力系数.

2 柔轮三维实体模型的建立

2.1 主要几何参数

为了实现模型的参数化设计，本文模型的建立、分析、后处理等过程采用APDL语言.建模时，为计算方便，空载传动状态下的柔轮齿圈采用1/4柔轮模型对称约束；在β=25°处建立四滚轮波发生器并添加接触定义，波发生器作用在齿圈的中部；柔轮齿根过渡圆角处网格划分较密.

柔轮轮齿示意图如图1所示，选用有限元软件ANSYS进行建模和分析.

选取柔轮轮齿的结构参数如表1所示.

2.2 平面齿圈的建立

当齿轮用滚刀或插刀切削时，渐开线齿廓表达式为［9］

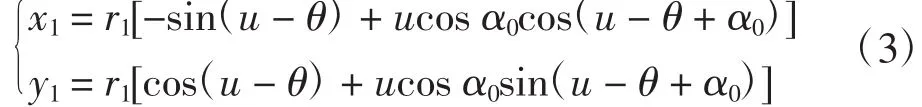
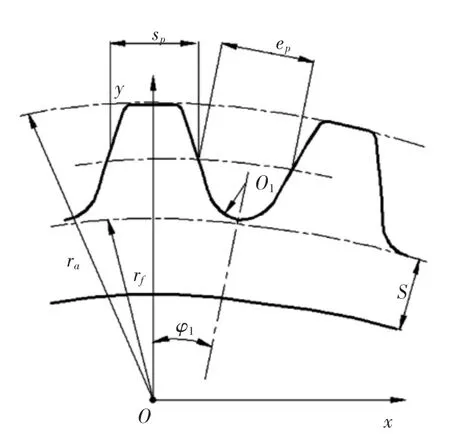
图1 柔轮轮齿示意图Fig.1 Diagram of flexpline tooth profile

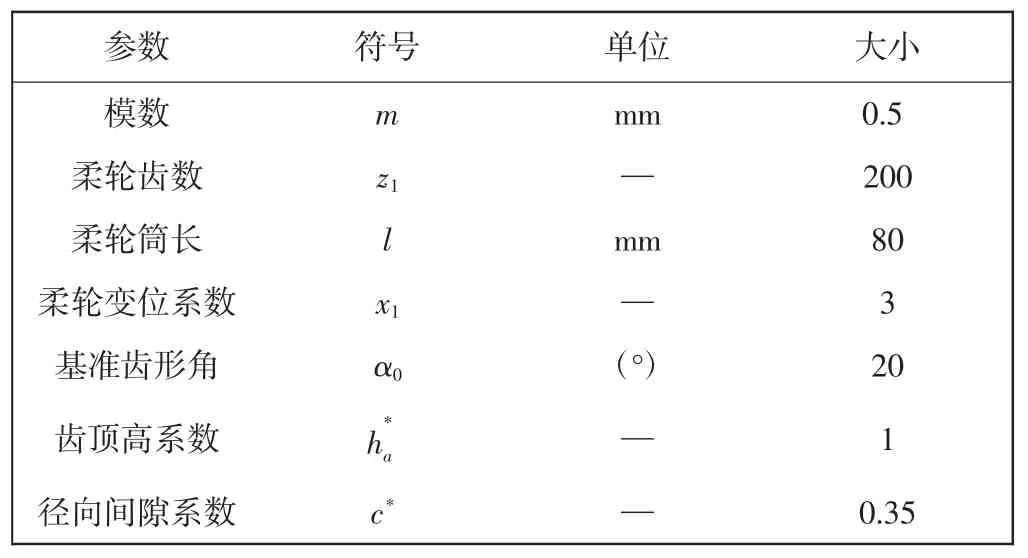
表1 柔轮轮齿的参数Tab.1 Parameters of flexible tooth

式中：r1为柔轮分度圆半径；u为系刀具沿被切齿轮的分度圆作无滑动的滚动时之转角；α0为基准齿形角；θ为齿轮分度圆齿厚所对中心角的1/2.

柔轮采用滚动加工时，其渐开线齿廓的几何尺寸计算公式如表2所示.

表2 渐开线柔轮齿廓的几何尺寸计算公式Tab.2 Calculation formulas for geometric dimensions of involute tooth profile of flexpline

根据图1的柔轮轮齿简图和表1、表2中的柔轮参数，利用APDL语言，确定柔轮的齿顶圆和齿根圆的位置.再结合柔轮的渐开线方程式（3）确定渐开线齿廓的点的坐标.采用点-线-面的方法，生成半个齿，再将半个齿镜像生成一个完整的齿，通过阵列生成1/4轮齿，如图2所示.

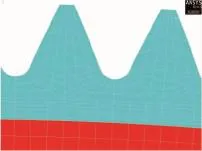
图2 平面齿圈模型Fig.2 Model of planar tooth ring

2.3 三维实体模型的建立

将平面齿圈沿轴向拉伸，生成三维实体模型.基于图3结构模型和表3结构参数添加柔轮筒体.

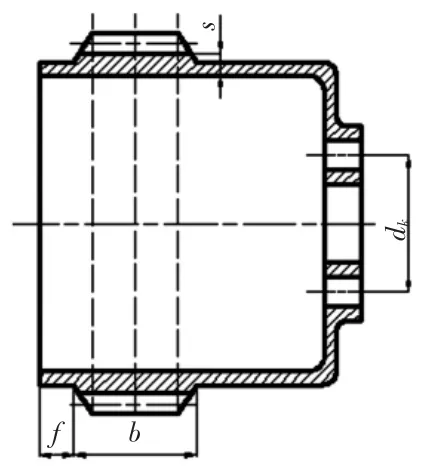
图3 柔轮结构简图Fig.3 Structure diagram of flexpline

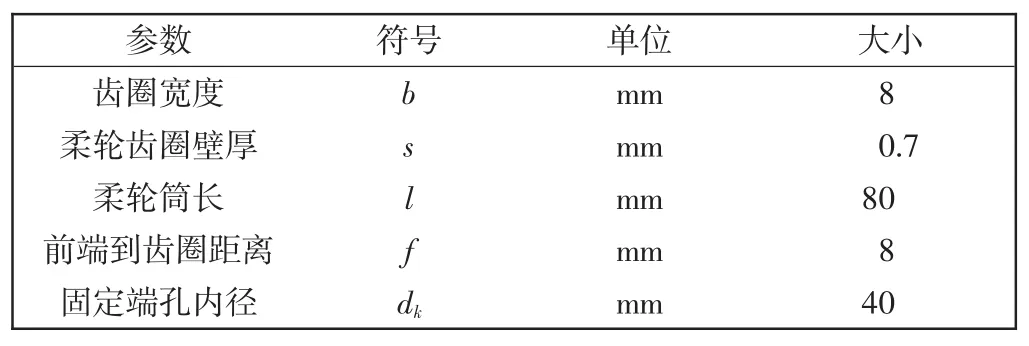
表3 柔轮筒的结构参数Tab.3 Structural parameters of flexible cylinder

利于APDL语言，在网格剖分时，将齿的底面与柔轮筒上与实体齿圈接触的部分周向均分和轴向均分一致，使两者剖分后的节点位置一一对应.通过APDL语言中“Nummrg”命令来实现节点合并.获得如图4所示三维实体模型.

图4 柔轮三维实体模型Fig.4 3D solid model of flexpline

3 实体有限元模型的应力分析

3.1 平面齿圈的应力分析

计算理论值和规范值时，选取中性圆半径rm= 50.375 mm，选取径向变形系数为1，则平面齿圈最大径向位移w0=m=0.5 mm.取E=210 GPa，KM=1，Kd=1，Cσ=1.5［17］.

平面齿圈中，沿柔轮筒的径向壁厚分为3层.齿根圆半径处设为顶层，柔轮筒中面设为中层，柔轮筒的内壁设为底层，如图5所示.

图5 径向分层示意图Fig.5 Radial layer diagram of flexpline

定义波发生器与柔轮筒内表面之间为线-线接触，利用ANSYS软件对平面齿圈进行有限元计算分析，得到柔轮的应力云图，如图6所示.

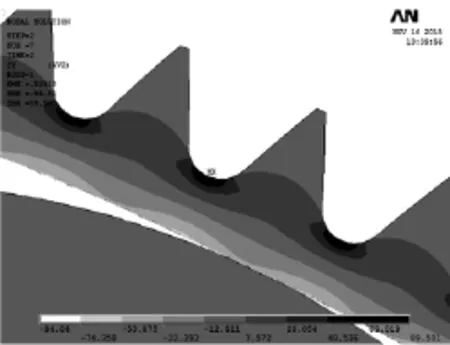
图6 平面齿圈应力云图Fig.6 Stress nephogram of planar tooth ring

根据在图5所示定义的3条路径，提取顶层、中层、底层应力.由于中层应力较小，在-6.5～7.5 MPa之间，对柔轮影响不大，不作讨论.提取平面齿圈的顶层应力与式（1）的理论值比较，如图7所示.齿圈发生弯曲变形时，顶层受到拉应力，底层受到压应力，提取平面齿圈的底层应力，与由式（1）计算得到的理论值的相反数比较，可以得到比较曲线如图8所示.

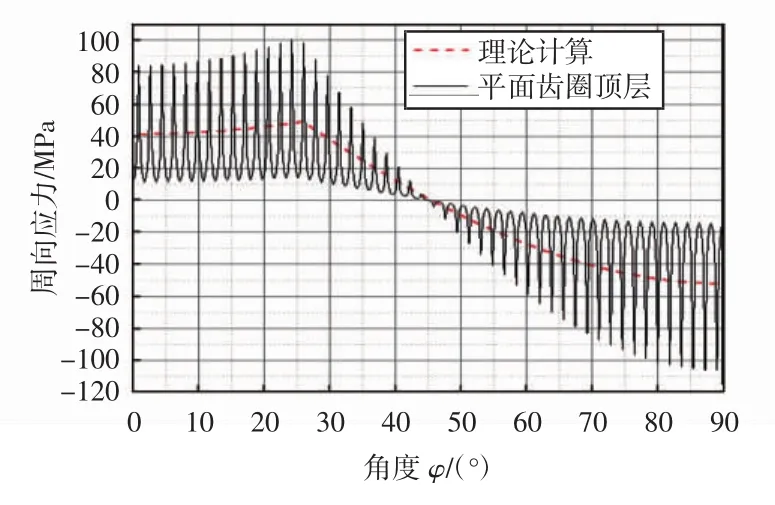
图7 平面齿圈顶层周向应力与理论值比较Fig.7 Circumferential stress distribution in top layer of planar tooth ring and theoretical result

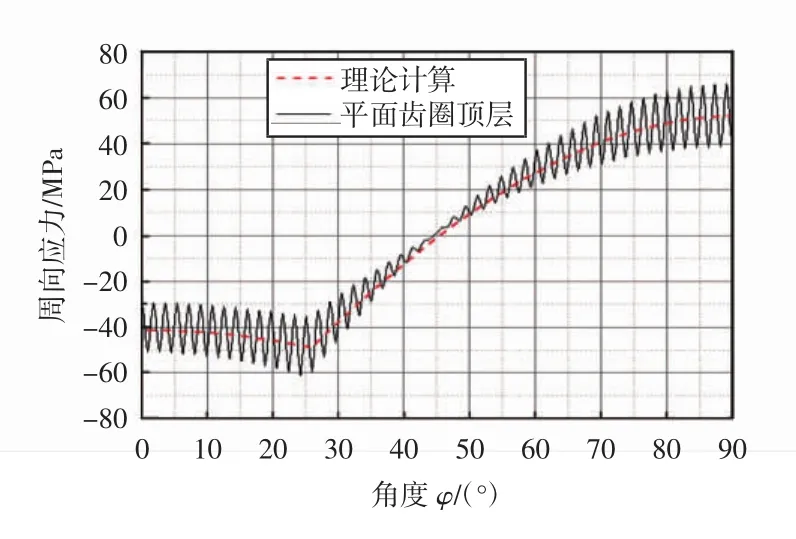
图8 平面齿圈底层周向应力与理论值比较Fig.8 Circumferential stress distribution in bottom layer of planar tooth ring and theoretical result

基于式（1）等效圆环理论的最大值为52.2 MPa，发生在柔轮短轴处；在柔轮与波发生器接触处，理论值为49 MPa.由式（2）设计规范获得最大周向弯曲应力为74.5 MPa.

通过图7和图8平面齿圈的应力可以发现，各层沿周向应力分布是不均匀的.应力波动幅度在柔轮的短轴、长轴和波发生器接触处较大，在φ=45°部位最小.沿着周向应力波动的均值的变化趋势与理论计算值基本一致.

如图7所示，平面齿圈顶层上最大周向应力为106.2 MPa，发生在柔轮短轴处，比理论值大103.4%，比设计规范值大42.6%；在柔轮与波发生器接触处，平面齿圈顶层周向应力为100.2 MPa，比理论值大51.1%，比设计规范值大34.5%.

如图8所示，平面齿圈的底层上最大周向应力为66 MPa，发生在柔轮短轴处，比理论值大25.4%，比设计规范值小11.4%；在柔轮与波发生器接触处，平面齿圈底层周向应力为61 MPa，比理论值大24.5%，比设计规范值小18.1%.

3.2 三维实体模型的应力分析

把平面齿圈轴向拉伸，生成三维实体齿圈.沿齿圈的轴向方向，把柔轮的齿宽分为图9所示的前、中、后3个截面.

图9 轴向分层示意图Fig.9 Axial layer diagram of flexpline

定义波发生器与柔轮筒内表面之间为面-面接触，利用ANSYS软件对三维实体模型进行计算分析，求解获得柔轮三维实体模型的应力云图，如图10所示.

图10 柔轮三维实体模型应力云图Fig.10 Stress nephogram of 3D flexpline model

平面齿圈模型与三维实体齿圈的中截面是对应的，故提取三维实体模型中截面上的应力，与平面齿圈模型计算结果进行比对分析.提取三维实体模型中截面上顶层和底层的周向应力如图11、图12所示.

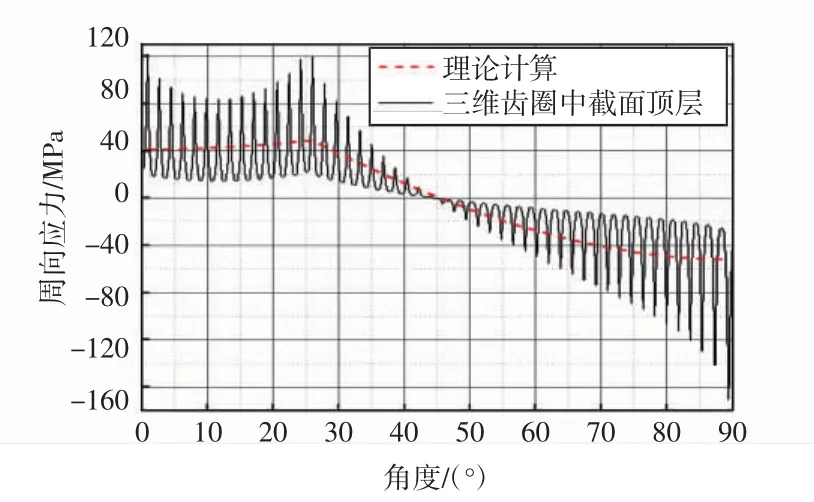
图11 三维实体模型中截面顶层周向应力与理论值比较Fig.11 Circumferentialstressdistributionintoplayerinmiddle section of 3D solid model and theoretical result

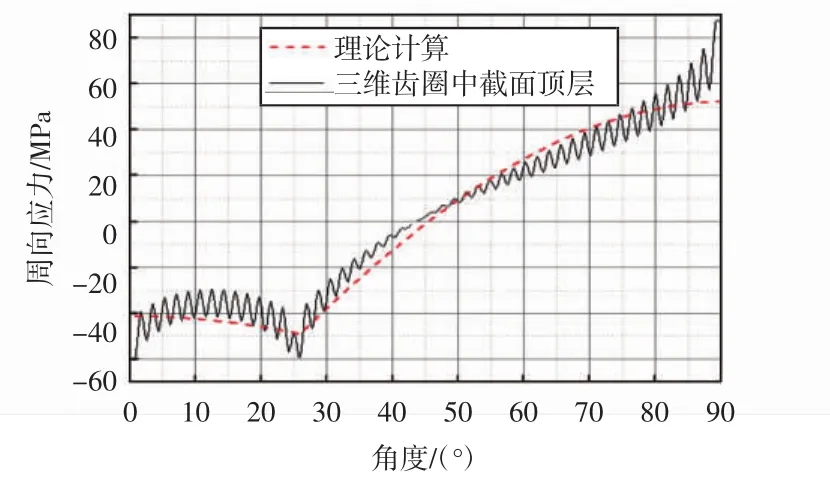
图12 三维实体模型中截面底层周向应力与理论值比较Fig.12 Circumferential stress distribution in bottom layer in middle section of 3D solid model and theoretical result

如图11所示，三维实体模型中截面顶层最大周向为170.3 MPa，发生在柔轮筒短轴处，比平面齿圈大60%，比理论值大226%，比设计规范值大129%.在波发生器与柔轮接触处，中截面周向应力为120 MPa，比平面齿圈大20%，比理论值大145%，比设计规范值大61%.

如图12所示，三维实体模型中截面底层最大周向为88 MPa，发生在柔轮短轴处，比平面齿圈大33%，比理论值大69%，比设计规范值大18%.在波发生器与柔轮接触处，中截面底层周向应力为60 MPa，与平面齿圈的相等，比理论值大22%，比设计规范值小19%.

通过图11和图12三维实体模型的应力曲线发现，三维实体模型内沿周向应力波动的均值的变化规律与理论值基本一致.但无论在顶层，还是在底层，三维实体模型的应力计算结果都大于平面齿圈模型计算结果.这是由于平面齿圈没有轴向应力，在三维实体模型中的应力为双向应力，中截面在弯曲状态下产生轴向应力，使周向应力增大.

4 结论

使用参数化建模方法，在ANSYS中利用APDL语言建立包含渐开线齿廓的柔轮有限元实体模型，通过设置波发生器与柔轮的接触关系，分析柔轮在空载状态下的应力，获得更为接近柔轮实际情况的应力结果.

（1）平面齿圈有限元实体模型中，沿周向应力波动均值与理论计算值基本吻合.

（2）平面齿圈有限元实体模型的周向应力计算表明：柔轮齿圈上的周向应力在底层较小，在顶层最大；顶层齿槽底部的周向应力均比规范值大.

（3）三维实体模型中的中截面上最大周向应力也发生在顶层，但相比于平面齿圈，周向应力极值都偏大.三维实体模型中截面顶层最大周向比理论值大2倍以上，比设计规范值大1倍以上.

［1］MUSSER C W.Strain wave gearing：US，2906143［P］.1959-09-01.

［2］辛洪兵.柔轮齿圈应力的有限元分析［J］.机械科学与技术，2003，22（4）：558-559. XIN H B.Finite element analysis of the stress of flexible tooth ring［J］.Mechanical Science and Technology，2003，22（4）：558-559（in Chinese）.

［3］向国齐．谐波齿轮传动柔轮有限元分析研究 ［D］．成都：四川大学，2005．XIANG G Q.Finite element analysis and study of flexspline in harmonic drive［D］.Chengdu：Sichuan University，2005（in Chinese）.

［4］ KAYABASI O，ERZINCANLI F.Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modeling［J］.Materials&Design，2007，28（2）：441-447.

［5］秦磊，许立忠．机电集成静电谐波传动柔轮的应力分析［J］．机械传动，2007，31（6）：13-15．QIN L，XU L Z.The stress analysis of the flexible of the electromechanical integrated electrostatic harmonic drive［J］.Mechanical Transmission，2007，31（6）：13-15（in Chinese）．

［6］王知行，徐克．杯型柔轮的应力分析与研究［J］．齿轮，1989，13（2）：23-26．WANG Z X，XU K.Stress analysis and study of cup-shaped flexspline［J］.Journal of Gear，1989，13（2）：23-26（inChinese）．

［7］韩建华，范祖尧．谐波传动中杯形柔轮的应力分析 ［J］．齿轮，1987，11（5）：6-10. HAN J H，FAN Z R.Stress analysis and study of cup-shaped flexspline in harmonic drive［J］.Journal of Gear，1987，11（5）：6-10（in Chinese）.

［8］CHEN X X，LIU Y S，XING J Z，et al.A novel method based on mechanical analysis for the stretch of the neutral line of the flexspline cup of a harmonic drive［J］.Mechanism and Machine Theory，2014，76：1-19.

［9］CHEN Xiao-xia，LIN Shu-zhong，XING Jing-zhong.Modeling of flexspline and contact analyses of harmonic drive［J］. Key Engineering Materials，2010，419/420：597-600.

［10］付军锋，董海军，沈允文.谐波齿轮传动中柔轮应力的有限元分析［J］.中国机械工程，2007，18：2210-2214. FU J F，DONG H J，SHEN Y W.The finite element analysis of the stress of flexible in harmonic drive［J］.Chinese Mechanical Engineering，2007，18：2210-2214（in Chinese）.

［11］刘文芝，张乃人，张春林，等.谐波齿轮传动中杯形柔轮的有限元计算与分析［J］.机械工程学报，2006，42（4）：52-57. LIU W Z，ZHANG N R，ZHANG C L，et al.The finite element calculation and analysis of the cup-shaped flexible in harmonic drive［J］.Journal of Mechanical Engineering，2006，42（4）：52-57（in Chinese）.

［12］吴伟国，张勇，梁风.具有啮合齿面接触对的谐波传动有限元模型建立与分析［J］.机械传动，2011，12：37-41. WU W G，ZHANG Y，LIANG F.The establishment and analysis of the finite element model of harmonic drive with the contact of meshing tooth surface［J］.Mechanical Transmission，2011，12：37-41（in Chinese）.

［13］DONG H，TING K L，WANG D.Kinematic fundamentals of planer harmonic drives［J］.ASME J Mesh Des，2011，133（1）：（011007-1）-（011007-8）.

［14］DONG H，WANG D，TING K L.Kinematic effect of the compliant cup in harmonic drives［J］.ASME J Mech Des，2011，133（1）：（051004-1）-（051004-7）.

［15］董惠敏，张晓青.基于实验建模的谐波齿轮传动柔轮的有限元分析研究［J］.机械传动，200l，25（2）：16-19. DONG H M，ZHANG X Q.Finite element analysis of the flexible of harmonic with experimental model［J］.Mechanical Transmission，200l，25（2）：16-19（in Chinese）.

［16］陈晓霞.基于侧隙评价的谐波齿轮圆弧齿廓设计及状态仿真研究［D］.天津：天津工业大学，2012. CHEN X X.Design and simulation study of the arc tooth profile of harmonic based on backlash evaluation［D］.Tianjin：Tianjin Polytechnic University，2012（in Chinese）.

［17］机械设计手册编委会.机械设计手册单行本：轮系［M］.北京：机械工业出版社，2007：166-169. Mechanical Design Manual Editorial Board.Mechanical Design Handbook Offprint：Gear［M］.Beijing：Mechanical Industry Press，2007：166-169（in Chinese）.

Stress analysis of harmonic gear driven in assemble state with 3D solid finite element model

CHEN Xiao-xia1，2，CHENG Kai1
（1.School of Mechanical Engineering，Tianjin Polytechnic University，Tianjin 300387，China；2.Tianjin Key Laboratory of Modern Mechatronics Equipment Technology，Tianjin Polytechnic University，Tianjin 300387，China）

In order to describe the tooth profile and dedendum stress distribution of harmonic flexspline correctly，a 3D solid model method based on real tooth profile is put forward.Using involute tooth profile as an example，a parameterized solid model based on language APDL is set up，which includes important parameters such as involute tooth profile，tooth thickness and tooth root fillet.The stress of flexspline under the action of wave generator is obtained by defining contact between the wave generator and flexspline's inner surface.The stress is compared with the theoretical value based on equivalent ring theory.In order to analyze the stress distribution of flexspline in assemble state more fully，a 3D solid model of flexspline is built and solved by ANSYS.The stress is extracted by defining the path in the middle section corresponding to the section calculated by theoretical formula and compared with the results obtained by the planar gear ring and theoretical value.The results show that in the finite element model of planar gear ring，the mean value of the circumferential stress fluctuation is consistent with the theoretical value，which validates the validity of the finite element model method.In addition，the circumferential stress extracted from 3D solid model is larger than that from planar gear ring，and the maximum circumferential stress occurs at the top layer.

harmonic gear；flexspline；finite element analysis；3D solid model；assemble state

TH112.2

A

1671-024X（2016）05-0077-06

10.3969/j.issn.1671-024x.2016.05.014

2016-03-09

国家自然科学基金面上项目（51575390）；天津市应用基础与前沿技术研究计划一般项目（14JCYBJC19200）

陈晓霞（1969—），女，博士，副教授，主要研究方向为谐波齿轮传动、数字化设计制造.E-mail：chenxx@tjpu.edu.cn