基于特征参数的脉搏波高斯拟合

汪剑鸣，惠 芳，韦 然

（天津工业大学电子与信息工程学院，天津 300387）

基于特征参数的脉搏波高斯拟合

汪剑鸣，惠 芳，韦 然

（天津工业大学电子与信息工程学院，天津 300387）

由非创伤性测量获得的脉搏波可由若干个高斯函数合成，提出一种得到最优高斯拟合脉搏波信号的方法.首先提取能反映人体心血管系统生理病理信息的一些特征参数，然后选择其中的一个或多个特征参数作为评价高斯拟合效果的标准，最后依据这些标准得到最优的高斯拟合脉搏波信号.由于依据该方法得到的拟合脉搏波信号的一些重要特征参数与实测脉搏波信号最为接近，因而更能真实地反映人体心血管系统的生理病理状态.

特征参数；脉搏波；高斯函数拟合；血压；特征比例；波形特征量；增强指数

form characteristics；augmentation index

血压是血液在动脉中流动时作用于血管壁所产生的压力［1］.血压是否正常是健康与否的重要判断依据之一，检查血压是临床上判断疾病和观察治疗效果的一大方式.动脉的血压从主动脉和大动脉传播到小血管和微血管的过程形成了动脉脉搏波，当人体心血管发生异常时，动脉系统会发生变化，从而导致脉搏波的波形发生相应的改变［2-3］.所以现有的一些检查都试图从脉搏波的压力及波形变化中提取各种生理病理信息［4-6］.

近年来，为了揭露脉搏波信号的生理病理信息出现了许多的脉搏波合成的方法.所有方法的原理都是把一个周期的脉搏波信号分解为若干个独立波，然后再进行相关的研究［7］.现有的脉搏波信号分解思想主要有2种：一种为依据脉搏波的产生机理进行分解；另一种为依据脉搏波的波图进行分解.

脉搏波的产生，简单的说就是心脏的搏动使血管内的血液以波的形式沿着动脉传播而产生的，在传播过程中会受到血管阻力的影响从而产生回波［8］.依据这一产生机理可见脉搏波信号分解为前向波和反向波2个部分.

一般认为，由非创伤性测量获得的脉搏波图主要由主波峰、重博波以及重搏前波组成［9］.钱伟立等［10］根据脉搏波的这一特性提出了一种由3个高斯函数（钟形波）合成脉搏波的数学模型.该数学模型不仅能合成各种常见的脉搏波，而且通过高斯函数的参数能得到反映正常人年龄和心血管疾病的特征值.但是该方法仅仅局限于用3个高斯函数来拟合，过于单一，不能判断出其拟合效果是否为最优.

为了得到一个最优的高斯拟合脉搏波信号，本文提出了一种方法.该方法通过计算不同数量的高斯拟合脉搏波与实际采集的脉搏波的特征参数的相对误差，得出基于脉搏波特征参数的评价标准，再依据所得标准得到最优的高斯拟合脉搏波信号.经过此方法判断后得出的拟合脉搏波更能真实地反映人体的动脉血压变化及人体心血管系统的生理病理状态.

1 脉搏波数据的采集及拟合

1.1 脉搏波数据的采集

本论文中的实验数据是通过 Biopac公司的MP150多导电生理记录仪采集得到，其中受测者均为身体状况良好的男性青年.受测者在测定开始前至少休息10 min后，由同一名测试员使用上述记录仪采集受测者左手食指指尖的脉搏波信号，在采集过程中受测者取坐位并保持静止.采集的指尖脉搏波信号如图1所示.

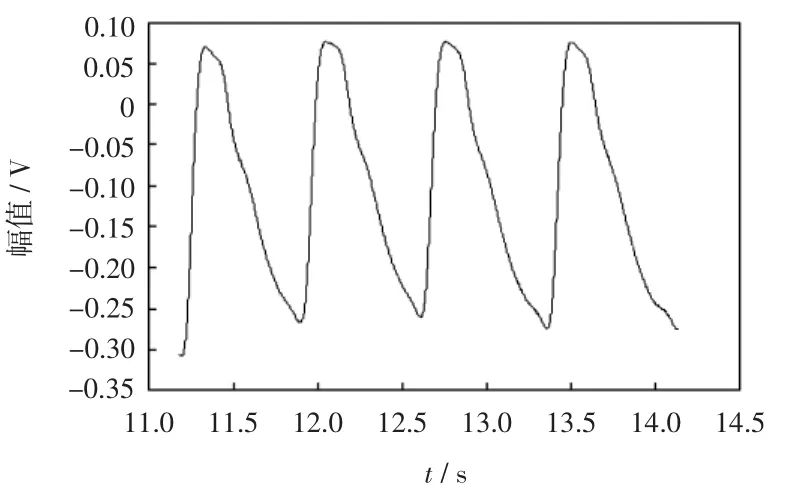
图1 MP150采集的脉搏波信号Fig.1 Pulse wave signal collected by MP150

1.2 高斯函数拟合

一个周期的外周动脉脉搏波可由若干个高斯函数合成，每一个高斯函数需要3个参数来确定，即幅度V、时间T和宽度U.总的脉搏波x（t）由下式表示：

式中：T为一周期脉搏波的长度.

根据式（1）对采集到的脉搏波数据进行拟合，本文通过改变高斯函数的个数进行了3种拟合，拟合结果如图2所示.

由图2中可以看出，随着高斯函数数量的增多，拟合波形越来越接近实测波形.

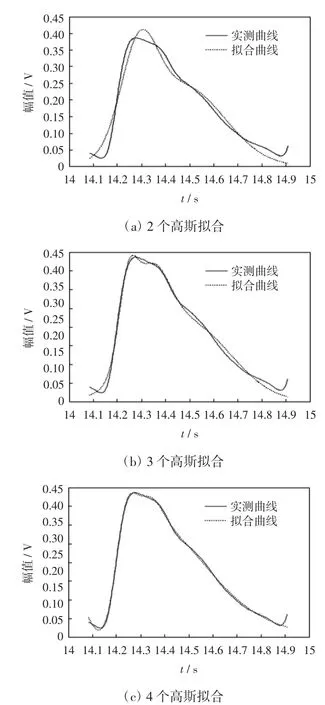
图2 高斯函数拟合结果Fig.2 Results of Gaussian fitting

2 脉搏波的特征参数

2.1 脉搏波波形特征量

本文中用于评估拟合效果的特征参数主要有脉搏波波形特征量K、收缩期波形面积K1、舒张期波形面积K2、特征比例K1/K2以及反射波增强指数AI.这些特征参数均能反应一些重要的生理病理信息.

脉搏波波形特征量K值是以脉搏波波图面积变化为基础进行提取的，虽然不能反映出脉搏波的一些细微的变化，但能反映一些重要生理参数如血管外周阻力、血管弹性和血液粘性等的变化［11-13］.其计算公式为：

由于K值相同时脉搏波的波图的形状也会有所差异，所以利用收缩期与舒张期分界点将脉搏波波图面积分为收缩期面积与舒张期面积2部分［14］，并在评估拟合效果的过程中加入这些脉搏波波形周期面积特征，即收缩期波形面积K1、舒张期波形面积K2及特征比例K1/K2［15］.其计算公式为：

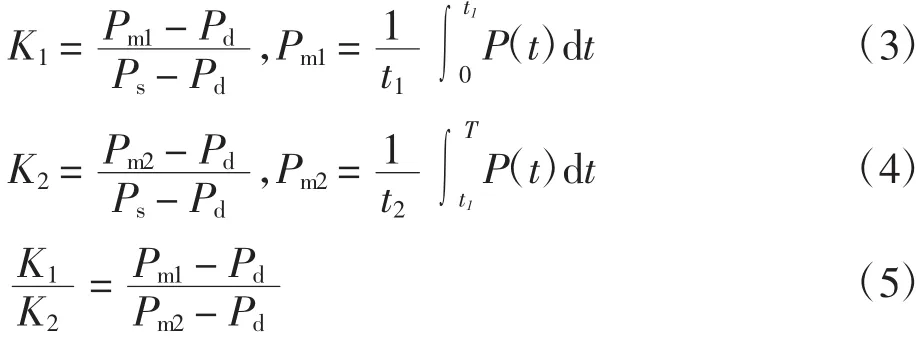
式中：Ps为收缩压；Pd为舒张压；Pm1为收缩期平均压；Pm2为舒张期平均压.

2.2 反射波增强指数

反射波增强指数（augmentation index，AI）是近年来临床研究中应用较为广泛的反映动脉反射波的指标，可间接地反映动脉硬化的程度［16-18］.其计算方法是用反射波和前向波融合后所达到的压力除以反射波发生前的最高压力［19］，如图3所示.计算公式为：

图3 增强指数AI计算方法Fig.3 Calculation method of augmentation index（AI）

3 数据的处理与分析

3.1 波形特征量的计算

采集4个身体状况良好的男性青年的脉搏波波形，根据以上的计算方法分别计算出这4个波形的脉搏波波形特征量K、收缩期波形面积K1、舒张期波形面积K2、特征比例K1/K2以及桡动脉反射波增强指数AI.其计算结果如表1所示.

表1 实测脉搏波特征参数计算结果Tab.1 Calculation results of characteristic parameter for measured pulse wave sign

对这4个实测波形分别进行2个、3个以及4个高斯函数的拟合，得到合成波，再计算所得合成波的波形特征参数.其计算结果分别如表2、表3以及表4所示.

表2 2个高斯函数合成脉搏波特征参数的计算结果Tab.2 Calculation results of characteristic parameter for two Gauss functions to synthesize pulse wave

表3 3个高斯函数合成脉搏波特征参数的计算结果Tab.3 Calculation results of characteristic parameter for three Gauss functions to synthesize pulse wave

表4 4个高斯函数合成脉搏波特征参数的计算结果Tab.4 Calculation results of characteristic parameter for four Gauss functions to synthesize pulse wave

3.2 拟合效果的比较

根据以上的计算结果分别得到了在不同拟合状态下的K′、K′1、K′2、AI′以及K1/K′2.分别计算这些特征参量与实测脉搏波特征参量K、K1、K2、AI及K1/K2之间的相对误差δ，通过δ来判断拟合的效果.相对误差δ的计算公式为：

式中：Δ为绝对误差；L为真值.

不同数量的高斯函数拟合时K′与K的相对误差对比图如图4所示.

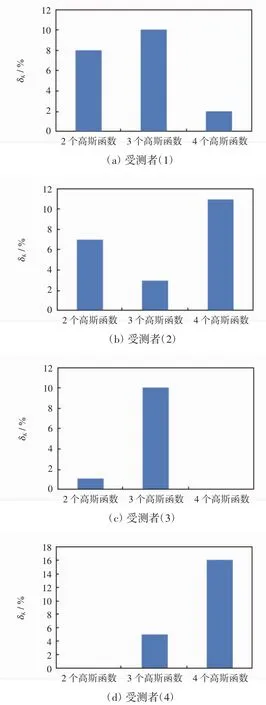
图4 不同拟合条件下K′与K的相对误差对比图Fig.4 Relative error comparison between K′and K under different fitting condition

由图4可见，受测者（1）与受测者（3）的δK的变化趋势一致，即拟合条件为3个高斯函数时δK的值最大，4个高斯函数时最小，2个高斯函数时相对误差介于中间水平.

不同数量的高斯函数拟合时K1值的相对误差对比图如图5所示.

图5 不同拟合条件下K′与K的相对误差对比图11Fig.5 Relative error comparison between K′1and K1under different fitting condition

由图5可见，受测者（2）、受测者（3）与受测者（4）δK1的变化趋势一致，即拟合条件为2个高斯函数时δK1的值最大，3个高斯函数时达到最小，4个高斯函数时介于中间水平.

不同数量的高斯函数拟合时K2值的相对误差对比图如图6所示.

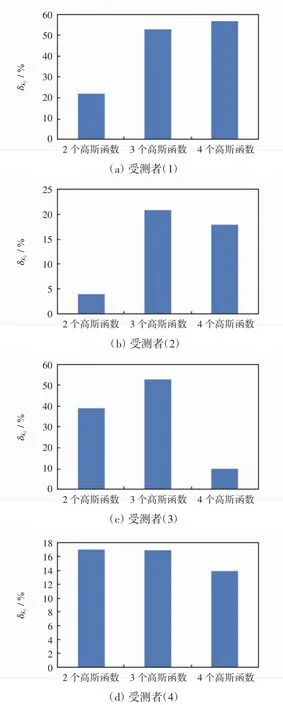
图6 不同拟合条件下的K′2与K2相对误差对比图Fig.6 Relative error comparison between K′2and K2under different fitting condition

由图6可见，受测者（1）、受测者（2）、受测者（3）以及受测者（4）δK2变化的趋势均不一致.

不同数量的高斯函数拟合时K1/K2值的相对误差对比图如图7所示.由图7可见，受测者（2与受测者（3）的δK1/K2的变化趋势一致，即拟合条件为2个高斯函数时δK1/K2的值最大，4个高斯函数时最小，3个高斯函数时介于中间水平.

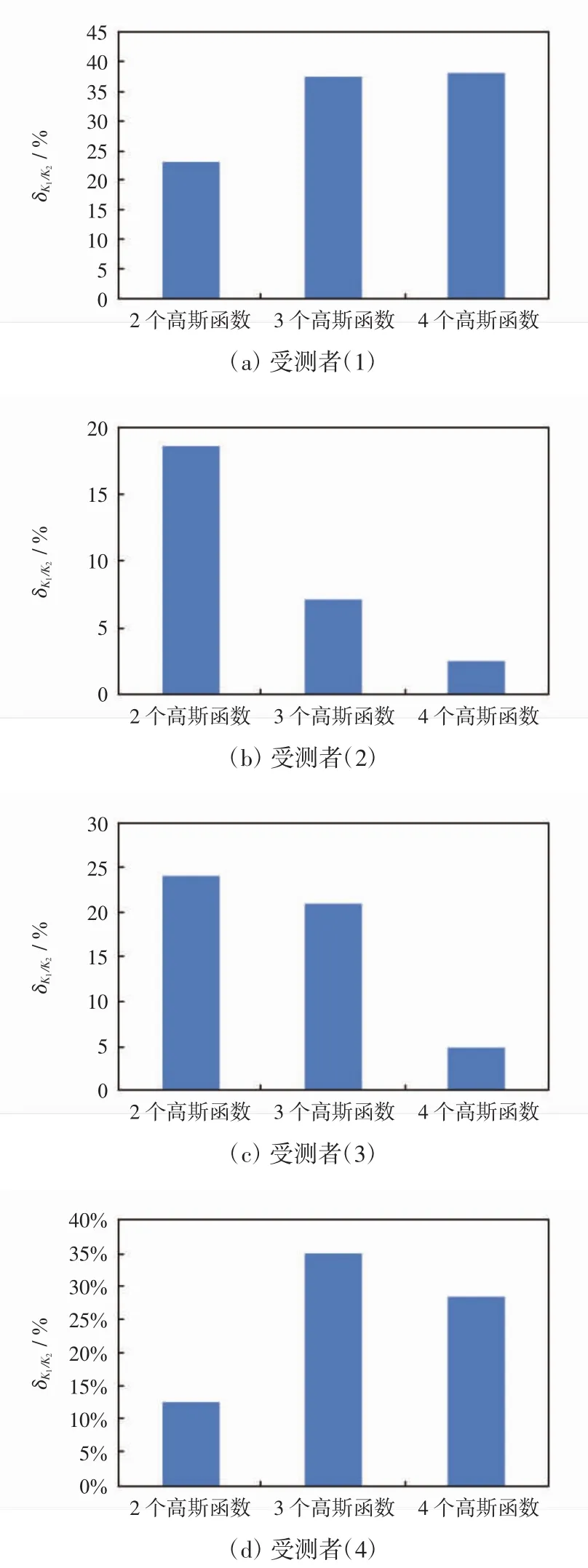
图7 不同拟合条件下K1/K′2与 K1/K2的相对误差对比图Fig.7 Relative error comparison between K1/K′2and K1/K2under different fitting condition

不同数量的高斯函数拟合时AI值的相对误差对比图如图8所示.

由图8可以看出，受测者（1）与受测者（3）δAI的变化趋势一致.即拟合条件为2个高斯函数时δAI的值最大，4个高斯函数时最小，3个高斯函数时介于中间水平.

图8 不同拟合条件下AI′与AI的相对误差对比图Fig.8 Relative error comparison between AI′and AI under different fitting condition

4 结论

通过上述4个受测者特征参量相对误差的比较，除舒张期波形面积K2的相对误差以外，脉搏波波形特征量K的相对误差、收缩期波形面积K1的相对误差、舒张期波形面积K2的相对误差、特征比例K1/K2的相对误差以及反射波增强指数AI的相对误差都有一定的变化规律.其中K的相对误差与AI的相对误差变化趋势一致，因此把这2个特征参量作为评价高斯拟合效果的标准.

将K的相对误差与AI的相对误差作为拟合效果的评价标准时，高斯函数个数为4个时拟合脉搏波与实测脉搏波的波形特征最为接近，能更好地反映人体的动脉血压变化及人体的生理病理信息.该方法为无创血压的标定提出了一个新的思路.

［1］李顶立.基于脉搏波的无创连续血压测量方法研究［D］.杭州：浙江大学，2008. LI D L.Research on noninvasive continuous blood pressure measurement based on the pulse wave［D］.Hangzhou：Zhejiang University，2008（in Chinese）.

［2］刘沛，庞宇，吴宝明，等.脉搏波形态特征与血压相关性的研究［J］.生命科学仪器，2015，13（2）：30-34. LIU P，PANG Y，WU B M，et al.Research of correlation between shape of the pulse wave and blood pressure［J］.Life Science Instruments，2015，13（2）：30-34（in Chinese）.

［3］SHU Jian-Jun，SUN Yu-guang.Developing classification indices for Chinese pulse diagnosis［J］.Complementary Therapies in Medicine，2007（15）：190-198.

［4］罗志昌，张松，杨文鸣，等.脉搏波波形特征信息的研究［J］.北京工业大学学报，1996，22（1）：71-79. LUO Z C，ZHANG S，YANG W M，et al.Research on characteristic information of pulse wave［J］.Journal of Beijing Polytechnic University，1996，22（1）：71-79（in Chinese）.

［5］孙薇，唐宁，江桂平，等.脉搏波波形信号特征点识别与预处理方法的研究［J］.生物医学工程学杂志，2015，32（1）：197-201. SUN W，TANG N，JIANG G P，et al.Study of characteristic point identification and preprocessing method for pulse eave signals［J］.Journal of Biomedical Engineering，2015，32（1）：197-201（in Chinese）.

［6］HLIMONENKO I，MEIGAS K，VAHISALU R.Waveform analysis of peripheral pulse wave detected in the fingertip with photoplethysmograph［J］.Meas Sci Rev，2003（2）：49-53.

［7］WANG Lu，XU Lisheng，FENG Shuting，et al.Multi-Gaussian fitting for pulse waveform using weighted least squares and multi-criteria decision making method［J］.Computers in Biology and Medicine，2013，43：1661-1672.

［8］MILLASEAU S C，KELLY R P，RITTER J M，et al.Determination of age-related increases in large artery stiffness by digital pulse contour analysis［J］.Clin Sci（Lond），2002，10（4）：371-377.

［9］张镜人，杨天权，郑秀春，等.脉搏波的线化理论对正常人桡动脉脉图和脉象分析［J］.中国生物医学工程学报，1987，6（3）：168-173. ZHANG J R，YANG T Q，ZHENG X C，et al.Analysis of the radial artery in normal people based on the linear theory of the pulse wave［J］.Chinese Journal of Biomedical Engineering，1987，6（3）：168-173（in Chinese）.

［10］钱伟立，徐兰义，陈富裕，等.高斯函数分解法提取脉搏波特征［J］.中国生物医学工程学报，1994，13（1）：1-7. QIAN W L，XU L Y，CHEN F Y，et al.Acquiring characteristic of pulse wave by gaussian function separation［J］.Chinese Journal of Biomedical Engineering，1994，13（1）：1-7（in Chinese）.

［11］罗志昌，程桂鑫，吴峥嵘，等.人体脉搏波波形参数与生理参数间关系的理论和实验研究［J］.北京工业大学学报，1988，14（2）：22-29. LUO Z C，CHENG G X，WU Z R，et al.Theoretical and experimental study on the relationship between pulse wave Shape and physiological parameters of human Body［J］.Journal of Beijing Polytechnic University，1988，14（2）：22-29（in Chinese）.

［12］WEBER T，O′ROURKE M F，LASSNIG E，et al.Pulse waveform characteristics predict cardiovascular events and mortality in patients undergoing coronary angiography［J］.J Hypertens，2010，8（4）：797-805.

［13］王安然，杨益民，杨琳，等.不同类型运动员桡动脉脉搏波波形及参数分析［J］.中国医学装备，2014，11（6）：27-31. WANG A R，YANG Y M，YANG L，et al.Analysisi on radial pulse waveform and parameters in different types of athletes［J］. China Medical Equipment，2014，11（6）：27-31（in Chinese）.

［14］柳兆荣.脉图与脉象的生物力学描述 ［J］.力学进展，1986，11（2）：114-124. LIU Z R.The biomechanical description of pulse graph［J］.Advances in Mechanics，1986，11（2）：114-124（in Chinese）.

［15］张俊利，蔺嫦燕，杨琳，等.脉搏波波形特征信息检测及与部分血流动力学变化相关分析［J］.生物医学工程与临床，2008，12（2）：104-107. ZHANG J L，LIN C Y，YANG L，et al.Detection of waveform characteristic of pulse wave and analysis of its related hemodynamic changes［J］.BME&Clin Med，2008，12（2）：104-107（in Chinese）.

［16］WEBER T，AUER J，O′ROURKE M F，et al.Arterial stiffness，wave reflections，and the risk of coronary artery disease［J］.Circulation，2004，109：184-189.

［17］FANTIN F，MATTOCKS A，BULPITTC J，et al.Is augmentation index a good measure of vascular stiffness in the elderly［J］. Age and Ageing，2007，36（1）：43-48.

［18］刘严，齐丽彤，马为，等.反射波增强指数与动脉硬化指数相关性的研究［J］.北京医学，2014，36（2）：84-87. LIU Y，QI L T，MA W，et al.The assiociation between augmentation index and arterial stiffness index［J］.Beijing Medical Journal，2014，36（2）：84-87（in Chinese）.

［19］肖文凯.桡动脉增强指数影响因素及与动脉血压关系的研究［D］.北京：军医进修学院，2010. XIAO W K.The main determinants of radial augmentation index and analysis of its relationship with blood pressure［D］. BeiJing：Chinese PLA Postgraduate Medical School，2010（in Chinese）.

Pulse wave Gaussian fitting based on characteristic parameters

WANG Jian-ming，HUI Fang，WEI Ran
（School of Electronics and Information Engineering，Tianjin Polytechnic University，Tianjin 300387，China）

Pulse wave obtained by noninvasive method can be synthesized by several Gauss functions，so a kind of method to get the best Gaussian fitting pulse wave signal was proposed.Firstly，some characteristic parameters reflecting the physiological and pathological information of human cardiovascular system were extracted.Then，one or more characteristic parameters were chosen as the standard for evaluating the effect of Gaussian fitting.Finally，a best Gaussian fitting pulse wave signal was acquired based on these standard.Because some important characteristic parameters of the fitting pulse wave signal obtained by this method are most closed to these of the measured pulse wave signal，reflects the physiological and pathological state of the human cardiovascular system thus it more accurately.

characterisitic parameters；pulse wave；Gaussian function fitting；blood pressure；characteristic ratio；wave

R318.11

A

1671-024X（2016）05-0059-07

10.3969/j.issn.1671-024x.2016.05.011

2015-11-19 基金项目：天津市应用基础与前沿技术研究计划（13JCYBJC37800）

汪剑鸣（1974—），男，博士，教授，主要研究方向为计算机视觉及应用、智能信息处理技术及系统.E-mail：wangjianming@tjpu.edu.cn