基于FEM-SPH耦合的离心机抛填土料冲击行为数值分析

钟卫洲， 杨玉明， 郝志明， 刘显军， 邓志方

(中国工程物理研究院 总体工程研究所，四川 绵阳 621999)



基于FEM-SPH耦合的离心机抛填土料冲击行为数值分析

钟卫洲， 杨玉明， 郝志明， 刘显军， 邓志方

(中国工程物理研究院 总体工程研究所，四川 绵阳 621999)

利用有限元(Finite Element Method, FEM)与光滑粒子流体动力学方法(Smoothed Particle Hydrodynamics, SPH)耦合的方法对离心机抛填土料动力响应进行分析，数值模型中离心机结构部件采用传统拉格朗日单元，土料采用无网格光滑粒子，实现了无黏性土料连续冲击离心机结构行为的数值再现。基于土料以5 m/s、10 m/s速度分别冲击离心机料斗与土料箱底算例进行分析，获得了离心机抛填结构在土料连续冲击作用下的应力分布和等效冲击载荷；在5 m/s速度冲击料斗冲击过程中，最大应力出现在离心机支撑装置横截面处，料斗结构上产生的最大等效应力为292 MPa；土料10 m/s冲击土料箱计算时，箱体底部铺设的橡胶垫层能降低冲击载荷幅值，实现对土料箱体结构的有效缓冲作用。数值分析结果表明，结合FEM高计算效率特点以及SPH耦合方法易于处理大变形优势，FEM-SPH耦合方法可以实现对土料类离散体冲击大变形行为数值模拟，有助于提高结构动态大变形响应过程模拟的逼真度和置信度。

土料冲击；冲击动力学；离心机；无网格方法；FEM-SPH耦合

某离心机抛填装置在100 g重力场下将无黏性土料抛入土料箱中，形成不同的断面和厚度，给试验者提供一种动态下的模型成型手段。离心机抛填装置工作时，土料从容器进入料斗、再由料斗抛填进入土料箱，此过程料斗和土料箱将面临冲击载荷。为了确保离心机抛填装置在运行过程中的安全性，需对装置整体结构在土料冲击下的动态响应进行计算。基于模型网格进行运算的有限元方法(Finite Element Method, FEM)是解决科学和工程问题的最有效的数值方法之一，但传统的有限元分析难以对离散土料体的连续运动过程及大变形行为进行有效模拟。严重扭曲有限元单元面临网格重构问题, 同时网格的异形扭曲将使得时间积分步长过小, 严重增加计算工作量[1-3]。而无网格方法不涉及单元网格细化或重建问题，计算时效不依赖网格尺寸，弥补了上述基于网格算法的缺陷，成功解决了对冲击动力学问题的结构大变形破坏行为高效数值仿真的问题。无网格法目前主要分为两类：一类是以Lagrange方法为基础的粒子法，如光滑粒子流体动力学法(Smoothed Particle Hydrodynamics， SPH)；另一类是以Euler方法为基础的无格子法，如无格子Euler/N-S算法(Gridless Euler/Navier-Stokes Solution Algorithm)等[2,4]。

近年国内外学者在无网格算法及精度提高方面开展了大量工作，KHAYYER[5]采用修正的不可压缩SPH方法对波浪破碎行为进行了模拟，基于变分原理实现了不可压缩SPH方程的角动量保全，修正后的模型实现了对波浪破碎以及破碎后行为的数值再现。赵光明[6]利用新型的无网格方法-再生核质点方法对高速冲击过程进行数值模拟，引入Bordner-Partom本构模型来实现材料高速冲击条件下的大应变和高应变率的特性。VIDAL[7]针对传统SPH显式分析过程中大扭曲变形导致的零能量和拉伸不稳定问题，提出了稳定的更新拉格朗日公式，相对于完全拉格朗日计算方法，新方法所消耗的计算资源更小。JUTZI[8]运用SPH方法对空间飞行多孔材料体碰撞行为进行了模拟，采用了多种压缩模型分析多孔材料冲击压缩行为模型的有效性，数值计算获得的弹性波速度、幅值与理论结果吻合一致。马新建[9]基于借鉴非结构网格方法下的耗散模型,给出了一种无网格法下求解三维Euler方程的具体实现形式,并对弹丸在超音速下不同马赫数、不同攻角的绕流流场进行了数值模拟。徐绯[10]推导了高阶一致性核函数的公式，构造了适用于SPH方法的简化线性一致性核函数，发现随着核函数一致性的提高，数值计算精度不断改善。SPH计算方法的改进有助于数值模拟精度与效率的提高，目前很多学者[11-15]利用SPH方法在结构冲击大变形领域开展了应用研究。

同时有限元与无网格耦合方法近年来被广泛用于分析材料结构大变形问题分析，FANG[16]采用有限粒子流体动力学方法(Finite Particle Hydrodynamics, FPH)和耦合粒子流体动力学 (Coupled Particle Hydrodynamics,CPH)两种改进SPH方法实现了对黏性流体自由面流动模拟。宋顺成等[17]在分析弹体侵彻混凝土问题时，为了描述混凝土的非线性变形断裂特性和保持分析过程中材料界面的清晰，将混凝土划分成光滑粒子并使用无网格光滑粒子动力学算法，而弹体保持传统有限元网格算法。AKTAY[18]分别采用SPH和FEM-SPH耦合方法对夹层碳纤维增强环氧树脂基复合材料板冲击行为进行了数值模拟，结果具有很高精度，能够弥补传统有限元难以有效模拟结构大变形造成单元扭曲行为的不足。THIYAHUDDIN[19]利用FEM-SPH耦合的方法模拟了含水防护结构冲击响应，分析了防护结构中的水晃动过程中能量吸收行为。由于FEM-SPH耦合方法具备有限元高计算效率及光滑粒子流体动力学方法易于处理结构离散大变形的优势，还有很多研究者[20-24]在其接触算法和工程问题应用方面开展了系列研究。

本文基于FEM-SPH耦合方法对该离心机抛填土料动力响应进行计算分析。通过数值模拟再现土料连续冲击离心机结构的运动过程，计算各结构部件在土料连续冲击作用下的应力分布和等效冲击载荷，考核离心机料斗和土料箱抗冲击性能；并结合理论与仿真结果，分析橡胶垫层对土料冲击缓冲动力学行为，获得FEM-SPH耦合方法对土料类离散体冲击大变形行为数值模拟的有效性认识。

1 SPH算法理论

有限元法在处理普通结构动态响应问题时具有较高的计算效率，但涉及结构大变形、单元严重扭曲、裂纹扩展等问题时常用网格重构，使其计算精度严重受损，计算效率也较低。无网格光滑粒子算法具备无需网格重构实现对结构大变形失效行为的模拟，但面临光滑粒子数量较多时需要消耗的计算资源。鉴于对模拟结果高精度和高计算效率的保证，通常采用FEM-SPH耦合方法对复杂结构冲击大变形行为进行数值模拟，对于小变形结构部件采用有限元单元，大变形扭曲部件则采用无网格粒子模拟，如图1所示。由于传统有限元理论方面的算法研究和工程应用已比较成熟，本文将不对此进行累述，主要针对SPH算法理论进行简单介绍。

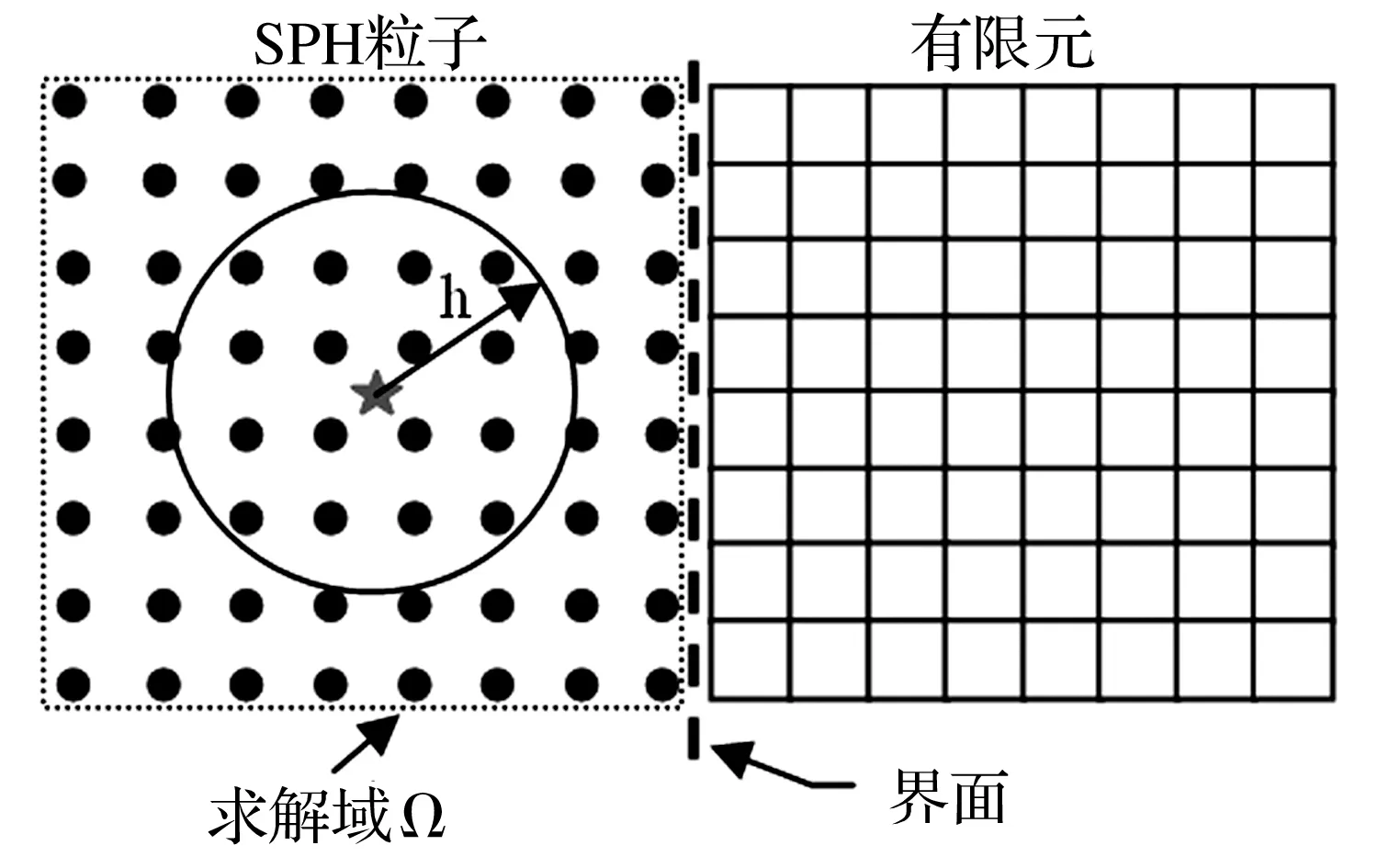
图1 FEM-SPH耦合示意图Fig.1 Schematic diagram of FEM-SPH coupling

SPH算法基础主要基于插值理论，将材料视为具有流体粒子性质的一组集合，每个单一光滑粒子具有材料、质量、速度等基本特性，代表一个已知物理参量的插值基点。计算中将连续动力学守恒的粒子偏微分方程转化为粒子场内的积分方程，所有运算基于离散粒子场积分进行。SPH算法包括核插值和粒子插值两种近似方法，在图1所示求解域Ω内通过特定的插值核函数W(x,h)，将密度、速度和压力等任一宏观变量的估值f(x)在空间x处通过场函数f(x′)在域内进行积分得到[18]：

f(x)=∫Ωf(x′)W(x-x′,h)dx′

(1)

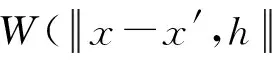
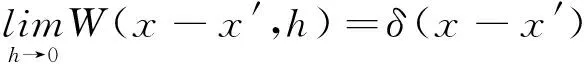
(2)

根据归一化条件，求解域Ω内δ(x-x′)函数积分值为1，即：

∫ΩW(x-x′,h)dx′=1

(3)

无网格光滑函数的数值近似基于其微分守恒方程的物理本质，SPH函数精度及其如何代表材料行为可以通过泰勒级数展开形式来认识。假设核估值函数f(x)是光滑函数，f(x′)泰勒级数展开形式为：

f(x′)=f(x)+f′(x)(x′-x)+

(4)

式中:r是泰勒级数第k阶导数近似后的系数，结合式(1) 和式(5)有：

(6)

(7)

将上述方程与连续介质力学粒子的质量守恒、动量守恒、本构方程进行联立，离散化便可进行求解获得我们需要的物理量；同时转化成规则的差分方程或全应力张量空间中的SPH算法插值公式后也能进行求解。

2 离心机抛填装置

2.1 计算结构模型

某离心机抛填装置总体结构如图2所示，由土料容器、料斗、支柱、支板、支撑装置及土料箱组成。支撑装置通过土料箱上的安装孔位固定，其上安装有液压缸-滑轨机构以及传感器检测系统，用来控制料斗装置的行程和抛填；容器装置通过支柱和支板固定在支撑装置上。

在离心机抛填装置工作过程中主要面临两个冲击问题，土料从容器向料斗填充过程，以及土料由料斗向土料箱抛填过程。土料在上述两个过程均具有一定运动速度，同时土料向土料箱抛填过程在100 g离心环境下进行。因此为了确保抛填装置结构在工作环境下的安全性，需对土料冲击作用下抛填装置结构的应力分布和冲击载荷进行计算。结合抛填装置整体结构及对称运动边界条件特点，忽略非承力电子器件，对抛填装置结构进行简化建模。建立的土料分别以5 m/s、10 m/s速度冲击料斗、土料箱的1/2简化模型如图3(a)和图3(b)所示。结合抛填装置工作原理和实际工作条件，对土料箱底部沿三个方向转动和轴向平动进行约束，并对模型对称面施加对称边界条件。由于在传统有限单元法中，单元的变形过大容易导致矩阵奇异，使得计算精度降低甚至无法求解下去，很难实现对离散土壤颗粒体运动变形行为进行模拟。因此为了数值实现土料粒子对料斗、土料箱连续冲击模拟现象，在计算中抛填装置各结构部件材料有限元网格，无黏性土料采用SPH光滑粒子进行模拟，土料SPH模型见图3虚线矩形框标注处。在土料冲击土料箱底模型中，考虑土料速度相对较高，在土料箱底布置10 cm厚橡胶垫层对土料冲击进行缓冲，降低土料对土料箱底的冲击载荷。

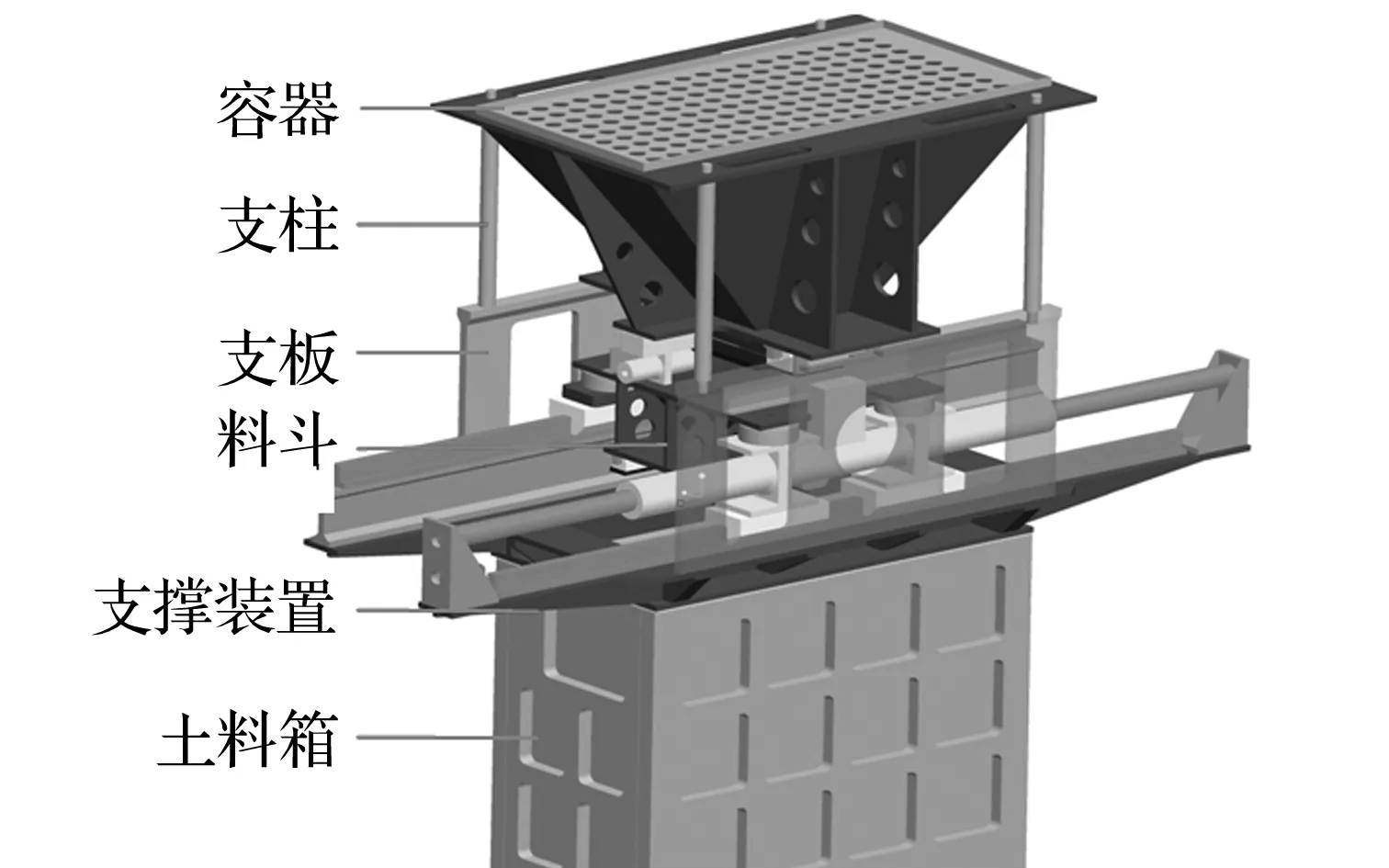
图2 抛填装置结构示意图Fig.2 Throw-filling equipment structure

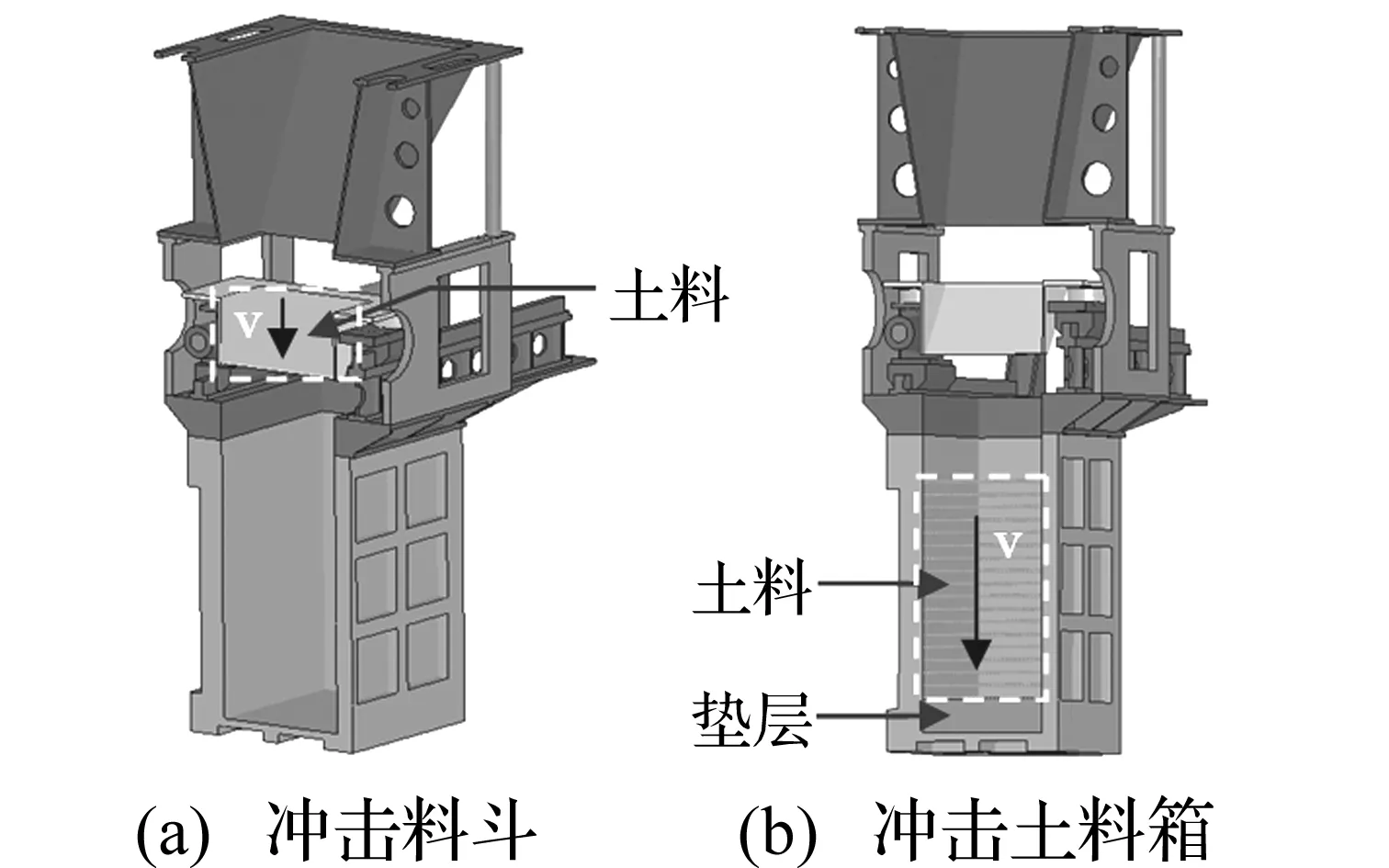
图3 土料冲击料斗和土料箱数值模型Fig.3 Numerical models of soil impacting hopper and soil box respectively

2.2 基本材料参数

离心机抛填装置结构材料主要涉及6061铝合金、Q690钢、无黏性土料和丁基橡胶。其中土料箱采用6061铝合金，离心机抛填装置其他部件采用Q690钢，土料箱底部缓冲垫层采用丁基橡胶。数值模拟中计算中选取的各材料力学性能参数如表1所示。

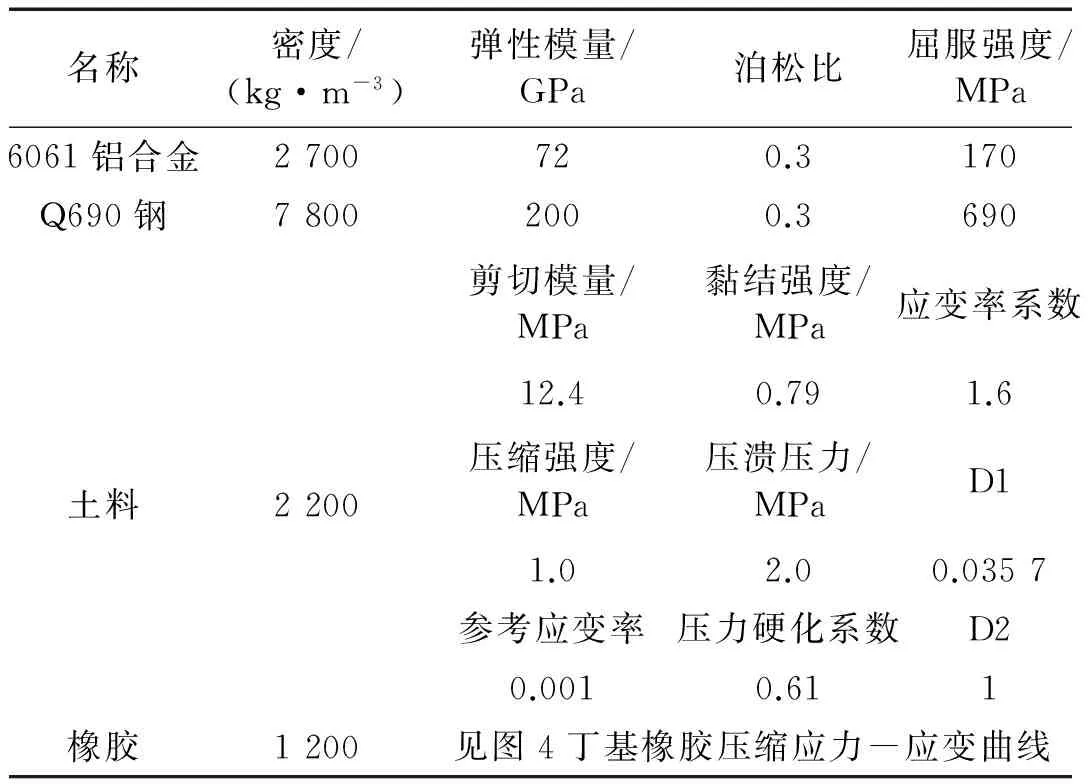
表1 材料力学性能参数表

对于超弹性橡胶材料的描述不涉及杨氏模量和泊松比，采用应变势能来表达应力-应变关系。橡胶材料采用DYNA中超弹性橡胶模型来描述，选取的橡胶单轴压缩实验测试工程应力-工程应变曲线如图4所示。

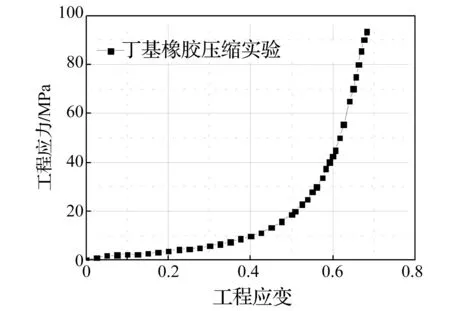
图4 丁基橡胶压缩应力-应变曲线Fig.4 Butyl rubber compression stress versus strain curve

3 土料冲击行为计算分析

3.1 土料5 m/s冲击料斗

离心机抛填装置工作工程中，土料以一定速度由容器进入料斗，土料对受边缘支撑、中部悬空的料斗形成一定冲击作用。为了分析土料冲击料斗是否对抛填装置稳定运行造成影响，需对整体结构在土料连续冲击料斗作用下的动力响应进行模拟。基于土料冲击料斗评估安全裕度考虑，数值模拟中采取土料以呈料斗形整体以5 m/s速度进入料斗，重力加速度取为9.8 m/s2。计算获得的土料冲击料斗过程如图5所示，从图中可以看出土料冲击在撞击料斗产生回弹，如图中矩形框标注。为了观察土料在料斗出口处的运动情况，数值料斗模型出口开启状态，有一部分土料从料斗底部出口两侧继续向下运动，如图中椭圆框标注处。

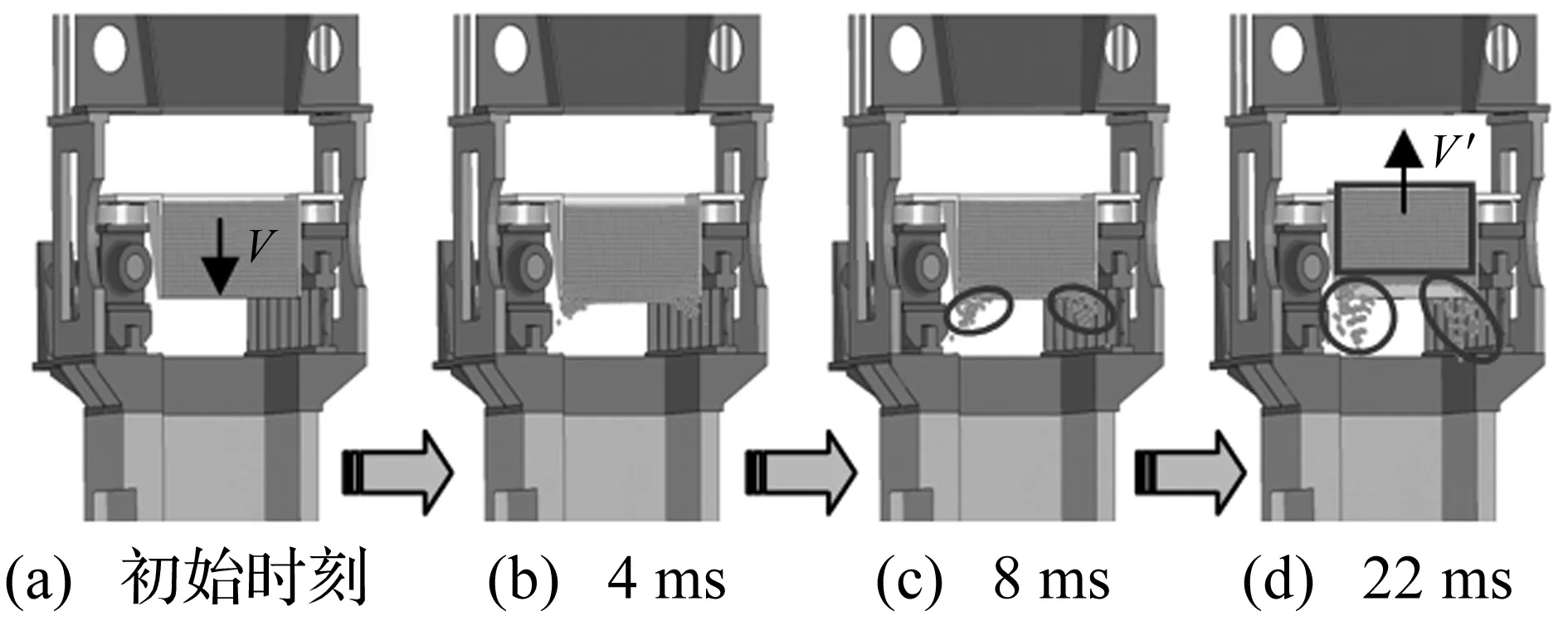
图5 土料冲击料斗过程Fig.5 Process of soil impacting hopper

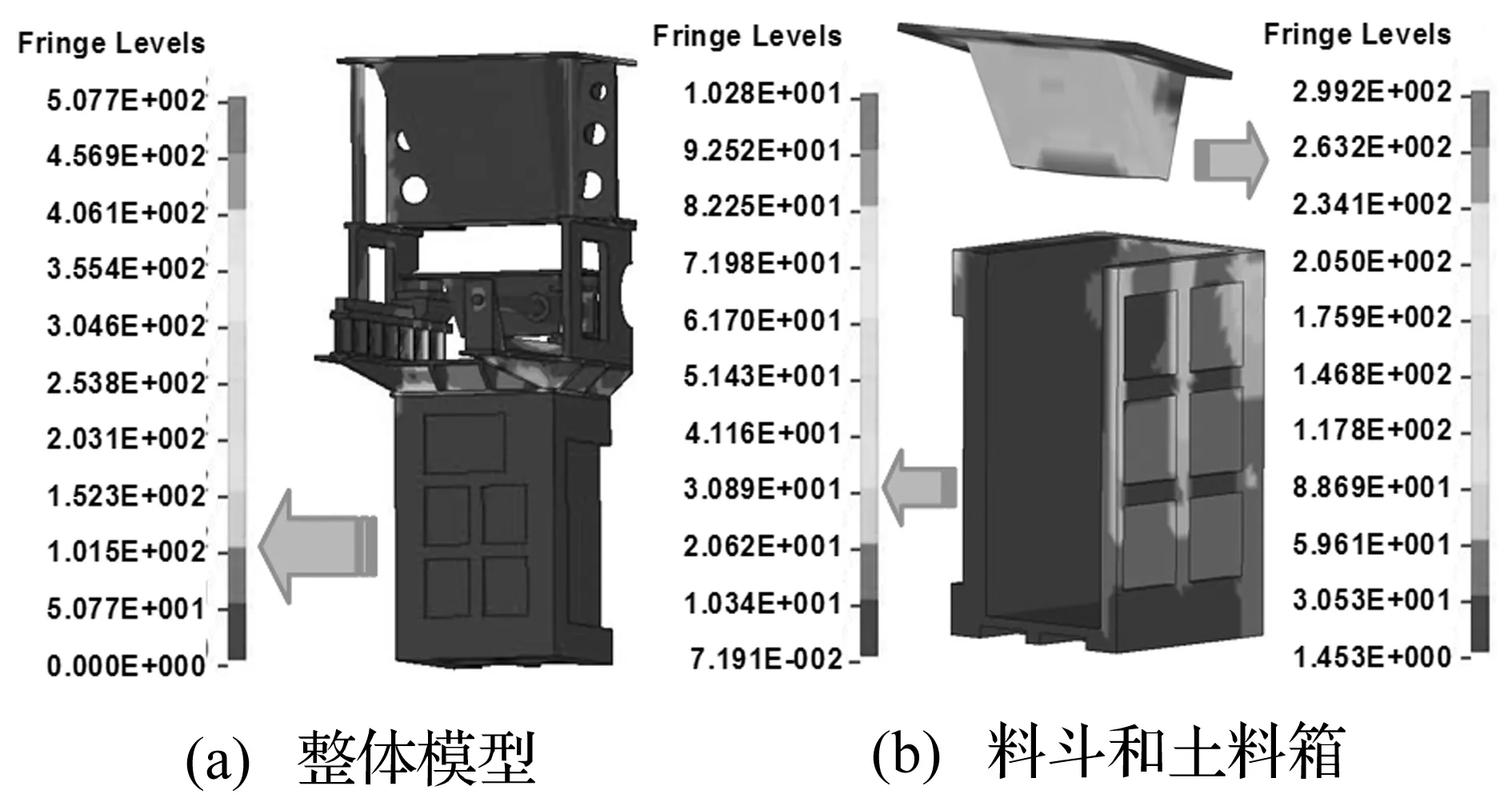
图6 等效应力分布图(土料5 m/s冲击料斗)Fig.6 Equivalent stress distribution for soil 5 m/s impacting hopper

土料冲击料斗过程中，抛填装置在最大应力时刻的等效应力分布如图6(a)所示，可以看出高应力区主要分布于支撑装置横截面突变处，应力为508 MPa；料斗应力分布如图6(b)上图所示，由于料斗边缘竖向位移被约束，土料冲击作用下料斗受力近似简支梁结构受均布载荷，因此在料斗底部中心位置产生应力最大，达到292 MPa；土料箱与支撑装置接触上端角处为较高应力分布区，应力为103 MPa，如图6(b)下图所示。由此可以看出在土料以5 m/s速度冲击料斗过程中，各部件结构最大应力均未达到材料屈服强度，离心机抛填装置结构设计和结构材料选取能承受土料由容器进入料斗时的产生冲击作用。

3.2 土料10 m/s冲击土料箱

离心机抛填装置在离心加速环境下开启料斗底部阀门，土料在惯性作用下以一定速度进入土料箱，形成对土料箱的抛填过程，并产生冲击作用。由于土料进入土料箱速度相对较高，因此在抛填装置设计中需对土料冲击土料箱的行为进行安全评估，计算土料冲击对抛填装置底部形成的冲击载荷，分析冲击载荷是否对离心机转臂正常运行造成影响。对离心机运行条件进行分析，选取土料10 m/s速度冲击土料箱进行计算，重力加速度取为9.8 m/s2。在首轮数值模拟针对土料直接对无缓冲垫层土料箱冲击响应进行分析，发现土料直接撞击土料箱形成冲击载荷较大，等效应力达到12.9 MPa，不能满足离心机结构设计要求，对离心机转臂正常运行造成安全隐患。

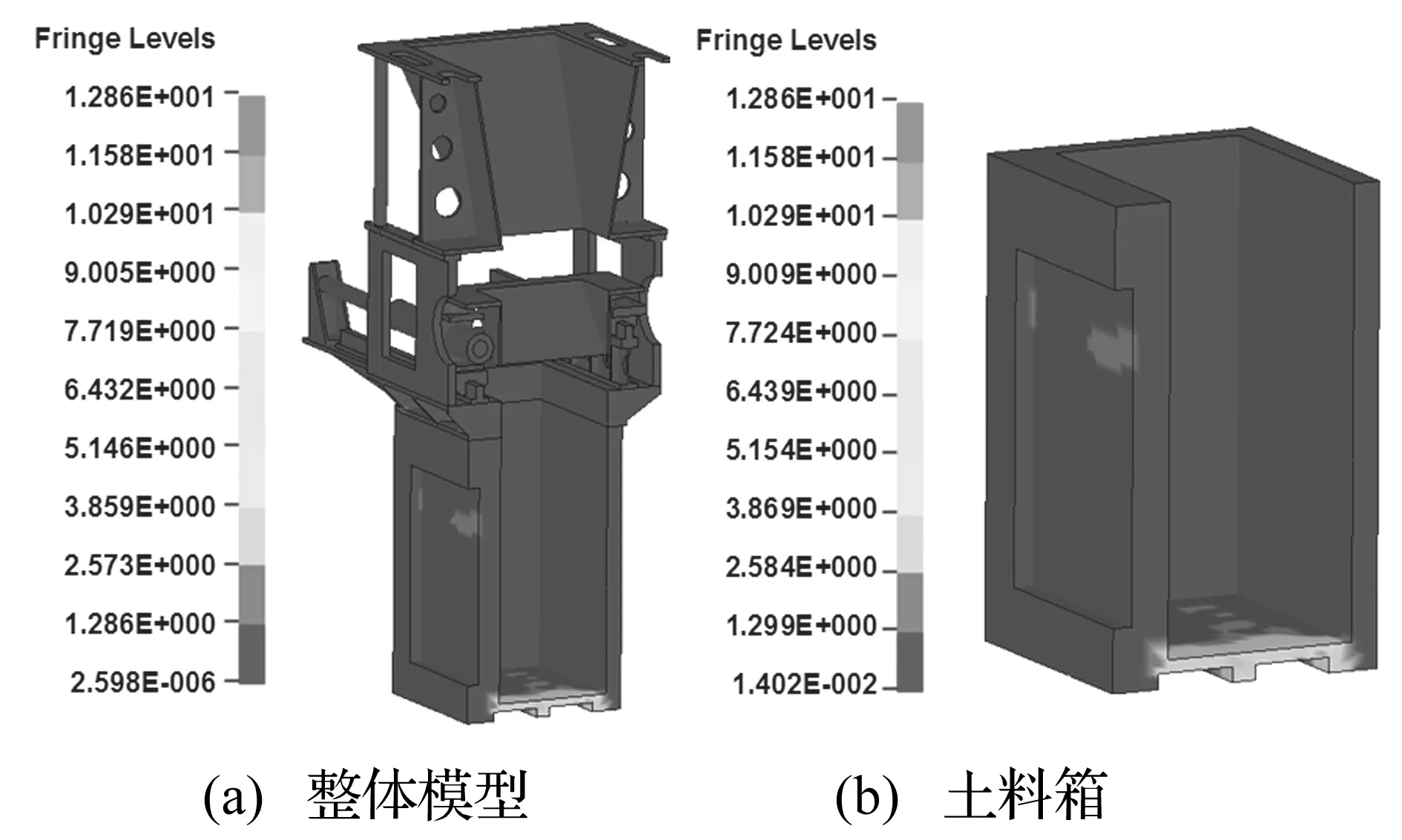
图7 等效应力分布图(土料10 m/s冲击土料箱,无垫层)Fig.8 Equivalent stress distribution for soil 10 m/s impacting soil box without cushion

因此为了离心机运行的安全性，采用在土料箱底部放置10 cm橡胶垫层对土料冲击进行缓冲效应数值分析，计算获得的土料冲击土料箱过程如图8所示，土料撞击土料箱底部后向侧面继续运动，达到土料箱内侧面后反弹继续运动。

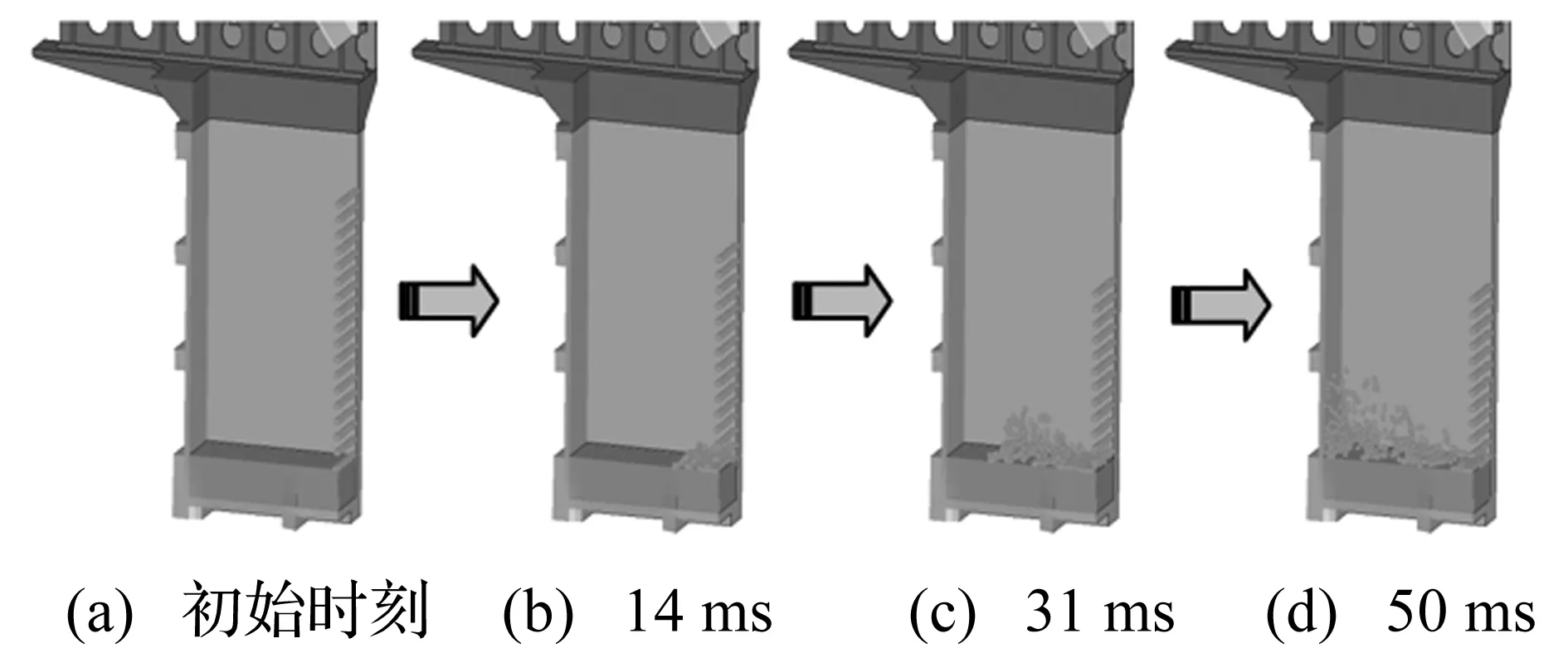
图8 土料冲击料斗过程Fig.8 Process of soil impacting soil box

图9 等效应力分布图(土料10 m/s冲击土料箱)Fig.9 Equivalent stress distribution for soil 10 m/s impacting soil box

计算得到的抛填装置等效应力分布如图9(a)和9(b)所示，高应力主要分布于土料箱粒子撞击处，最高应力约4.6 MPa，比无橡胶垫层低约60%；抛填装置其他部件在土料冲击土料箱过程中产生的应力很小，不超过1 MPa。土料箱底部形成的冲击载荷如图10所示，峰值载荷约90 kN，撞击后期表现为周期振荡曲线，产生的载荷值在离心机结构安全承载范围内。由此可见，在土料10 m/s速度冲击土料箱过程中，橡胶垫层能够实现对土料冲击缓冲作用，延长冲击载荷作用时间，有效降低抛填装置在土料抛填过程中对离心机产生的冲击载荷峰值，安全实现土料由料斗进入土料箱的抛填动作。

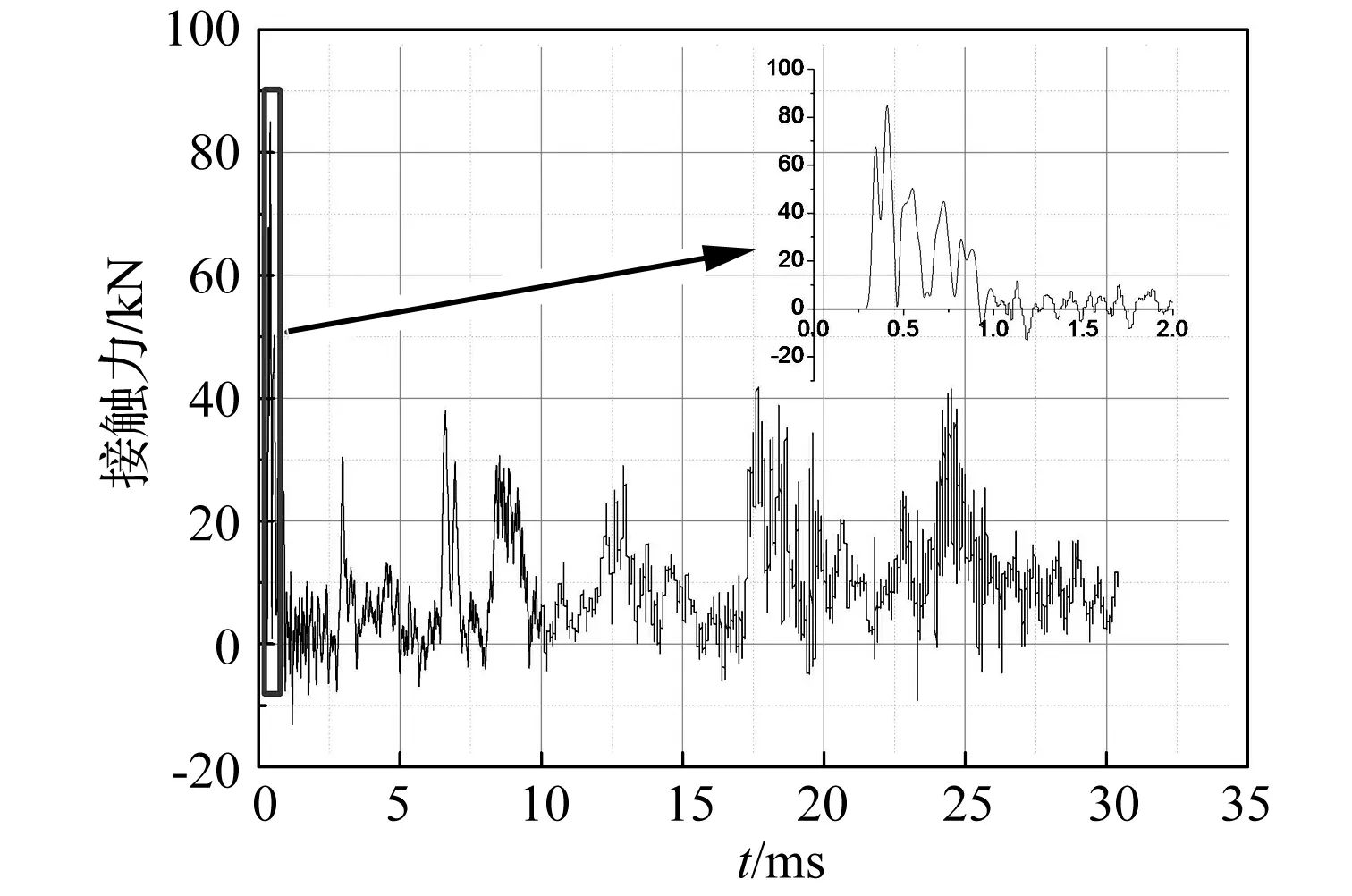
图10 土料箱底部冲击载荷曲线Fig.10 Impact loading curve on soil box bottom

4 橡胶垫层冲击缓冲效应分析

超弹性橡胶材料作为缓冲垫层放置于土料箱底部，主要利用低阻抗橡胶在冲击过程中形成较低作用力，同时依靠其弹性大变形增加土料与土料箱底部作用时间，从而降低撞击体间的作用力，实现对土料箱的冲击缓冲作用。基于一维应力波理论对土料与不同介质冲击碰撞进行简化分析，分析低阻抗橡胶材料在冲击过程中的缓冲效应。针对土料冲击土料箱建立的分析模型如图11所示，简化模型中忽略了三维效应及冲击后土料飞溅运动行为，该模型主要用于对土料与箱底冲击瞬时作用应力进行简化解析分析，从理论上认识不同冲击介质材料对土壤冲击效应的影响。冲击介质材料分别为铝合金和丁基橡胶材料，土料、铝合金和橡胶的密度和波速分别用(ρs,Cs)、(ρa,Ca)、(ρr,Cr)表示，土料冲击速度为v0，冲击作用产生的应力和速度为σ*和v*。

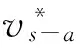
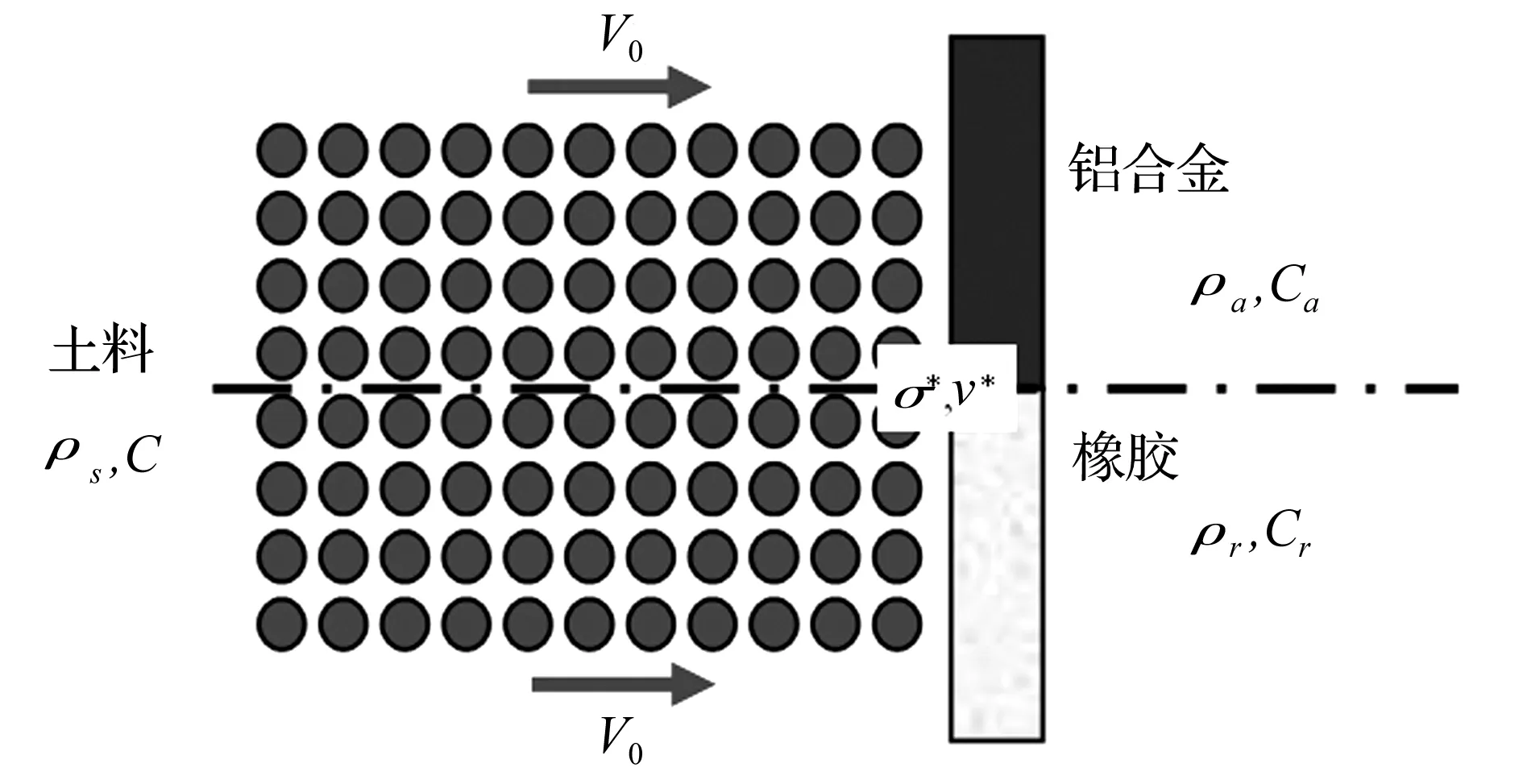
图11 土料-铝合金/丁基橡胶弹性碰撞简图Fig.11 Simplified elastic impacting diagram between soil and aluminium & butyl rubber

(8)

(9)

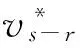
(10)

(11)

由于铝合金波阻抗大于橡胶波阻抗ρaCa>ρrCr，由式(10)、(11)不难可以看出，土料冲击铝合金土料箱底后的运动速度相对较小，但是产生的应力更大。低阻抗橡胶与土料撞击产生的应力较小，能够实现对土料箱底冲击缓冲作用。由于橡胶属于体积不可压超弹性材料，在离心机抛填装置缓冲设计中需注意弹性能释放、压缩膨胀变形问题。采用橡胶作为缓冲垫层使用时通常需对橡胶空间变形问题进行考虑，实际应用中应在橡胶四周预留足够空间供其压缩膨胀运动，避免橡胶垫层侧向膨胀对土料箱侧壁造成高应力挤压。

5 结 论

本文利用FEM-SPH耦合方法对土料冲击离心机抛填装置结构动力行为进行了数值模拟，再现了土料连续冲击离心机结构的运动过程，获得了结构部件在土料连续冲击作用下的动力响应，考核了离心机抛填装置结构的冲击安全性能。结合数值模拟结果和橡胶缓冲效应理论分析，可以获得以下结论：

(1) 基于FEM高计算效率特点以及SPH耦合方法易于处理大变形优势，FEM-SPH耦合方法可以实现对无黏性土料连续冲击过程的数值模拟，再现土料离散体冲击运动、碰撞飞溅过程，有助于提高结构动态大变形响应过程模拟结果精度。

(2) 离心机抛填装置结构能承受土料5 m/s速度进入料斗产生的冲击作用，土料冲击作用下抛填装置各部件应力均小于其材料屈服强度，支撑装置横截面突变处为高应力区，最大应力值为508 MPa；料斗底部中心位置产生的应力分布为292 MPa。

(3) 土料10 m/s速度冲击土料箱过程过程中，低阻抗橡胶垫层能实现对土料冲击缓冲作用，有效降低抛填装置在土料抛填过程中对土料箱的冲击载荷，安全实现土料由料斗进入土料箱的抛填动作。

(4) 橡胶通过低波阻抗、低幅值应力弹性储能特性实现对结构冲击缓冲作用，但体积不可压橡胶材料弹性储能为可逆过程，缓冲结构设计中需考虑橡胶弹性变形能释放和挤压侧向膨胀效应，合理预估橡胶弹性应变能释放影响；预留相应空间供橡胶变形运动，避免大变形压缩产生侧向高应力挤压现象。

[1] LI S, LIU W K. Meshfree and particle methods and their applications[J]. Applied Mechanics Reviews, 2002, 55(1): 1-34.

[2] 张雄, 刘岩, 马上. 无网格法的理论及应用[J]. 力学进展, 2009, 39(1): 1-36.

ZHANG Xiong, LIU Yan, MA Shang. Meshfree methods and their applications[J]. Advances in Mechanics,2009,39(1): 1-36.

[3] LIU M B, LIU G R. Smoothed particle hydrodynamics (SPH): an overview and recent developments[J]. Archives of Computational Methods in Engineering,2010,17(1): 25-76.

[4] VIGNJEVIC R, CAMPBELL J. Review of development of the Smooth Particle Hydrodynamics (SPH) method[M].Predictive Modeling of Dynamic Processes. Springer US, 2009: 367-396.

[5] KHAYYER A, GOTOH H, SHAO S D. Corrected incompressible SPH method for accurate water-surface tracking in breaking waves[J]. Coastal Engineering, 2008, 55(3): 236-250.

[6] 赵光明, 宋顺成, 杨显杰. 高速冲击过程数值分析的再生核质点法[J]. 力学学报, 2007, 23(1): 63-69.

ZHAO Guangming, SONG Shuncheng, YANG Xianjie. The reproducing kernel particle method for numerical analysis of high-speed impact process[J]. Chinese Journal of Theoretical and Applied Mechani, 2007, 23(1): 63-69.

[7] VIDAL Y, BONET J, HUERTA A. Stabilized updated Lagrangian corrected SPH for explicit dynamic problems[J]. International Journal for Numerical Methods in Engineering, 2007, 69(13): 2687-2710.

[8] JUTZI M, BENZ W, MICHEL P. Numerical simulations of impacts involving porous bodies: I. Implementing sub-resolution porosity in a 3D SPH hydrocode[J]. Icarus, 2008, 198(1): 242-255.

[9] 马新建, 谭俊杰, 任登凤. 三维无网格法及其在超音速弹丸流场模拟中的应用[J]. 弹道学报, 2010 (3): 54-57.

MA Xinjian, TAN Junjie, REN Dengfeng. Three dimensional meshless method and its application in supersonic flow field simulation of projectile[J]. Journal of Ballistics, 2010 (3): 54-57.

[10] 徐绯, 刘斌, 郑茂军, 等. 动态大变形计算模拟的无网格强积分核函数[J]. 中国科学: 物理学, 力学, 天文学, 2010 (9): 1174-1184.

XU Fei, LIU Bin, ZHENG Maojun, et al. The strong integrated kernel function in dynamic deformation simulations[J]. Scientia sinica phys, Mech & Astron,2010(9):1174-1184.

[11] 林晓东, 卢义玉, 汤积仁, 等. 基于 SPH-FEM 耦合算法的磨料水射流破岩数值模拟[J]. 振动与冲击,2014,33(18):170-176.

LIN Xiaodong, LU Yiyu, TANG Jiren, et al. Numerical simulation of abrasive water jet breaking rock with SPH-FEM coupling algorithm[J]. Journal of Vibration and Shock, 2014, 33(18): 170-176.

[12] LI W Y, YIN S, WANG X F. Numerical investigations of the effect of oblique impact on particle deformation in cold spraying by the SPH method[J]. Applied Surface Science, 2010, 256(12): 3725-3734.

[13] 王海兵, 寿列枫, 张建鑫, 等. 弹丸撞击下花岗岩靶破坏效应实验与数值分析[J]. 岩石力学与工程学报, 2014, 33(2): 366-375.

WANG Haibing, SHOU Liefeng, ZHANG Jianxin, et al. Experiments and numerical analysis of destructive effects of granite target under impact of projectile[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(2):366-375.

[14] 杨刚, 韩旭, 龙述尧. 应用SPH方法模拟近水面爆炸[J]. 工程力学, 2008, 25(4): 204-208.

YANG Gang, HAN Xu, LONG Shuyao. Simulation of underwater explosion near air-water surface by sph method[J]. Engineering Mechanics, 2008, 25(4): 204-208.

[15] MARUZEWSKI P, TOUZÉ D L, OGER G, et al.SPH high-performance computing simulations of rigid solids impacting the free-surface of water[J]. Journal of Hydraulic Research, 2010, 48(Sup1): 126-134.

[16] FANG J, PARRIAUX A, RENTSCHLER M, et al. Improved SPH methods for simulating free surface flows of viscous fluids[J]. Applied Numerical Mathematics, 2009, 59(2): 251-271.

[17] 宋顺成, 王庭辉, 才鸿年, 等. 钢制弹丸冲击混凝土时绝热剪切局部化的数值计算[J]. 爆炸与冲击,2007,27(3):246-250.

SONG Shuncheng, WANG Tinghui, CAI Hongnian, et al. Numerical calculations of adiabatic shearing localization of steel projectile impacting concrete[J]. Explosion and Shock Waves, 2007, 27(3): 246-250.

[18] AKTAY L, JOHNSON A F. FEM/SPH coupling technique for high velocity impact simulations[M].Advances in Meshfree Techniques. Springer Netherlands,2007:147-167.

[19] THIYAHUDDIN I, GU Y T, THAMBIRATNAM D P, et al. Impact & energy absorption of road safety barriers by coupled SPH/FEM[J]. International Journal of Protective Structures, 2012, 3(3): 257-274.

[20] 吕东喜, 黄燕华, 唐永健, 等. 基于 SPH 算法的磨粒冲击工件表面过程数值模拟[J]. 振动与冲击, 2013, 32(7): 169-174.

LÜ Dongxi, HUANG Yanhua, TANG Yongjian, et al. Simulating process of abrasive impacting a workpiece surface based on SPH method[J]. Journal of Vibration and Shock, 2013, 32(7): 169-174.

[21] JOHNSON G R, STRYK R A, BEISSEL S R. SPH for high velocityimpact computations[J]. Computer Methods in Applied Mechanics and Engineering,1996,139(1):347-373.

[22] 王维国, 陈育民, 刘汉龙, 等. 基于 SPH-FEM 耦合法的土体爆炸效应数值研究[J]. 岩土力学, 2013, 34(7): 2104-2110.

WANG Weiguo, CHEN Yumin, LIU Hanlong, et al. Numerical simulation of explosion in soil based on a coupled SPH-FEM algorithm [J]. Rock and Soil Mechanics, 2013, 34(7): 2104-2110.

[23] MCCARTHY M A, XIAO J R, MCCARTHY C T, et al.Modelling of bird strike on an aircraft wing leading edge made from fibre metal laminates-Part 2: Modelling of impact with SPH bird model[J]. Applied Composite Materials, 2004,11(5): 317-340.

[24] GUIDA M, MARULO F, MEO M, et al.SPH-Lagrangian study of bird impact on leading edge wing[J]. Composite Structures, 2011, 93(3): 1060-1071.

Numerical simulation for centrifuge throw-filling soil impact behavior based on FEM-SPH coupling

ZHONG Weizhou, YANG Yuming, HAO Zhiming, LIU Xianjun, DENG Zhifang

(Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China)

Soil continuous impact behavior of a centrifuge throw-filling equipment was simulated using finite element method & smoothed particle hydrodynamics (FEM-SPH) coupling method. Centrifuge structural components were modeled with Lagrangian finite elements and meshless smoothed particles were used for soil model in numerical simulation. Continuous impact processes of cohesionless soil.were reproduced numerically with FEM-SPH coupling. When soil impacting centrifuge hopper and soil box bottom at speeds of 5 m/s and 10 m/s,respectively, the stress distribution and equivalent impact load of the centrifuge structure were gained under soil continuous impacting condition. It was shown that the maximum equivalent stress is 292 MPa on the cross section of the centrifuge support device under the condition of soil impacting hopper at the spead of 5 m/s; rubber layer cushion on the soil box bottom can reduce impact loading amplitude when soil impacts the box bottom at speed of 10 m/s; the rubber layer can protect the box structure from soil’s continuously impacting; FEM simulation has a high computational efficiency and SPH method is a good way to describe structural large plastic deformation and damage, so the FEM-SPH coupling method can be applied to simulate soil-like material’s large deformation behavior, it is helpful for improving numerical simulation’s fidelity and confidence level.

soil impact; impact dynamics; centrifuge; meshless method; FEM-SPH coupling

国家自然科学基金(11302211;11390361;11472257)

2014-12-05 修改稿收到日期：2015-09-29

钟卫洲 男，博士，副研究员，1978年2月生

O347

A

10.13465/j.cnki.jvs.2016.19.034