自由磨料射流轴心磨料速度模型及分析

章文峰，卢义玉，汤积仁，陆晓辉，程玉刚

(1.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400030；2.重庆大学 复杂煤气层瓦斯抽采国家地方联合工程实验室，重庆 400030)

磨料射流是由固体颗粒(金刚砂、石英砂、陶粒等)与高速流动的水流或高压水流相互混合而形成的液固两相流[1]。因其切割破碎作业效率高、作业过程无热反应区、不发生化学反应等优点[2]，目前被广泛应用于石油、煤炭、机械等行业，如磨料射流油井割缝增产技术[3]、高压磨料射流割缝防突技术[4]、磨料射流抛光技术[5]等，另外磨料射流在辅助钻进硬岩[6]以及减少隧道开挖爆破振动[7]方面也有巨大的应用潜力。

磨料射流的磨蚀能力几乎全由磨料颗粒产生的，在磨料冲蚀过程中，磨料颗粒动能的大小决定着冲蚀对象是否产生塑性变形和形成裂缝，同时，材料侵蚀速率也完全取决于磨料速度[8-10]。

目前对前混合磨料射流切割深度的预测一直备受关注，如王瑞和[11]、董星[12]、周卫东[13]等提出的前混合磨料射流切割深度模型。但在他们的模型中，都没有体现出磨料速度这一关键参数。已有研究表明，磨料射流冲蚀岩石或金属材料时形成的冲蚀坑是一“V”形剖面，“V”形剖面最深处对应着磨料射流的轴心[14]。根据沈忠厚、李晓红等[15-16]的研究，磨料射流轴心流体速度是最大，而磨料的速度是通过与流体进行动量交换之后获得的。因此，在射流同一截面上，磨料射流轴心磨料速度最大。

为了确定前混合磨料射流切割最大深度，必须得出磨料在射流轴心处的速度。为此，笔者以自由磨料射流轴心磨料为研究对象，利用自由磨料射流轴心流体速度方程及磨料运动方程，建立自由磨料射流轴心磨料速度模型，基于等分法和迭代求解的数值求解方法，得出自由磨料射流轴心磨料速度，并利用PIV实验对磨料速度模型进行验证，为建立准确的磨料射流切割深度模型和实现磨料射流切割技术的定量控制提供可靠的理论支撑。

1 自由磨料射流轴心流体速度方程

根据Rajaratnam[17]和Boguslawski[18]等的研究，高压水射流经过喷嘴加速之后，以一种匀速状态通过喷嘴出口进入空气中，纯水射流进入空气后，其结构可分为初始段和基本段。纯水射流的具体结构如图1所示。初始段是指从喷嘴出口到等速核末端之间的射流区域。在等速核内，流体的速度与喷嘴出口的速度相等，而且流体速度大小、方向均相同。基本段，又被称为射流完全发展区域，是指等速核末端之后的区域。在基本段内，射流轴心速度与距离喷嘴出口距离成反比关系。

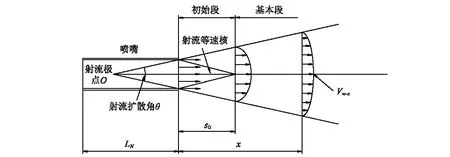
图1 纯水射流结构示意图Fig.1 Structure of water-jet flow in free air

射流等速核的长度与喷嘴出口流体速度无关，和喷嘴直径成正比,则射流等速核长度可以用以下公式表示：

S0=adN

(1)

根据不同学者的研究结论，射流等速核的长度介于4～9.22[19-22]倍的喷嘴直径之间，所以a=4～9.22。

假设喷嘴出口的速度为Vw-exit,根据纯水射流结构特性，射流轴心的流体速度沿着射流方向的速度分布可表示为：

(2)

在等速核末端，射流轴心的速度是相等的，于是有：

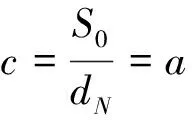
(3)

则公式(2)可简化为

(4)

2 自由磨料射流轴心磨料运动方程

自由磨料射流属于典型的湍流运动，因此可用BBO方程来描述磨料颗粒在自由磨料射流轴心的运动。自由磨料射流轴心磨料运动方程为

FD=Fg+Fp+Fa+FB+FS+FM+FL+FSm

(5)

方程左边为惯性力FD；方程右边分别为重力Fg、压差力FP、附加质量力Fa、Basset力FB、Stokes阻力FS、Magnus力FM、颗粒受到的升力FL和Saffman力FSm。

根据王明波等[23]的研究，当磨料颗粒从喷嘴喷出后，磨料颗粒受到的Basset力可以忽略。由于在自由磨料射流中，流体黏性的存在限制了磨料颗粒的旋转，磨料颗粒受到的Magnus力也可以忽略。由于流体速度梯度沿径向变化较慢，磨料颗粒所受到的Saffman力也可以忽略。另外，假设磨料颗粒是球形的，所以磨料受到的升力为零。由于磨料粒径较小，在计算过程暂时不考虑重力的影响。

所以自由磨料射流轴心磨料运动方程(5)可以简化为

FD=Fp+FS+Fa

(6)

对自由流场中单个颗粒的受力情况进行分析，得出公式(6)中各种力的表达式为

其中

式中：mp和ap分别为磨料质量及磨料加速度；Vw和Vp分别表示流体和磨料速度，m/s；dp为磨料粒径，m；ρw和ρp分别为流体和磨料的密度，kg/m3；CD为Stokes阻力系数,其值与雷诺数和两相速度差(VW-VP)有关；Re为雷诺数；dP/dx为沿射流方向的压强梯度，Pa·s；μ为流体的粘度Pa·s。

3 数值求解方法

将惯性力FD、压强梯度力FP、附加质量力Fa以及Stokes阻力FS的公式代入式(6)可得

(7)

从式(7)可以看出，磨料的加速度不是一个定值，求出该方程的显式解是非常困难的。为此提出了基于等分法和迭代算法的近似求解磨料速度的方法，即将磨料的运动距离等分为一定数量的线段，假设磨料在每一等分段内的运动过程中磨料加速度是一常数，利用在每一段内的终点速度又是下一分段内的起点速度这一特点，同时磨料在开始运动时的初始速度已知，利用迭代求解的方法，求出磨料整个运动距离的速度。

具体思路如下：假设磨料在喷嘴外流场轴心的运动位移为L，将磨料运动距离L等分为n段，s=L/n。在每一小段内，假设磨料的加速度是一定值，利用在每一段内的起点速度，即可求得在每一段的终点速度。假设，在第i段内，磨料的起始速度为Vpi，磨料在终点的速度为Vpi+1，磨料的加速度为api，那么他们之间满足以下关系

(8)

当运动距离s，api，Vpi已知时，则第i段运动距离的终点速度Vpi+1为

(9)

从式(9)中可以看出，磨料加速度在迭代过程中的表达式对求解式(9)至关重要。

在求式(9)之前，首先对dP/dx这一关键参数进行转换。图2为自由磨料射流轴心压强变化示意图。

图2 自由磨料射流轴心压强变化示意图Fig.2 Sketch map of pressure change of the centerline in free abrasive water jet

假设流体不可压缩，且忽略自由磨料射流轴心液相的重力势能，在第i段内，流体在起点时的速度为Vwi，压力为Pi。流体在终点时速度为Vwi+1，压力为Pi+1。根据质量守恒定律和伯努利方程可知

(10)

所以

(11)

由于假设流体在自由磨料射流中的流动属于定常流动，因此水的速度可以用位置x的函数表示，于是有

(12)

在初始段内，由于在轴心处流体的速度是相同的。因此，对自由磨料射流轴心磨料运动过程可分为初始段和基本段两个过程。结合式(7)、式(11)和式(12)，化简得到初始段和基本段第i段内磨料加速度表达式

(13)

式中：Vw对应初始段内轴心流体速度，Vpi对应初始段内第i段起点磨料的初始速度。Vwi和Vwi+1分别对应基本段内第i段的起点流体速度和终点流体速度，Vpi对应基本段内第i段的起点磨料速度。

表1 雷诺数Re与阻力系数CD取值公式Tab.1 Drag coefficient equations

当流体速度和磨料速度变化时，雷诺数也会变化的，对应的阻力系数也会随之变化。雷诺数与阻力系数之间的取值见表1[24]。

(14)

根据表1，当Re(i)时，即可确定CD(i)。

所以在迭代求解过程中，磨料加速度的表达式为

(15)

将式(15)代入式(9)即可得到磨料速度在迭代过程的表达式

(16)

利用参考文献[25]的方法得到喷嘴出口磨料速度，作为初始段内磨料的初始速度，利用式(16)可以计算得到初始段内磨料的速度。而初始段末端的磨料速度又是基本段内磨料的初始速度，利用式(16)可以得出基本段内磨料的速度。因此，可以得出自由磨料射流轴心任意位置处的磨料速度。

4 算例分析

算例条件：Vw-eixt=100 m/s，dN=0.004 m，ρp=2.7×103kg/m3,ρw=1.0×103kg/m3,dp=0.65×10-3m，s0=0.024 8 m，μ=1.14×10-3kg·m-1·s-1,基本段内的计算长度为0.045 2 m，喷嘴出口磨料速度为80 m/s。将上述参数代入迭代算法中，即可得到自由磨料射流轴心磨料速度、加速度以及雷诺数和阻力系数等参数，如图3～5所示的结果。

图3 自由磨料射流轴心流体速度和磨料速度变化趋势图Fig.3 Trend chart of fluid velocity and particle velocity at the centerline of free abrasive water jet

图3是自由磨料射流轴心流体速度与磨料速度随磨料运动距离的变化趋势图，从图中看出，流体从喷嘴喷出后，在初始段内，由于等速核的特性，流体速度保持不变，随后流体进入基本段，流体速度随着距离喷嘴出口距离的增大逐渐减小。而磨料从喷嘴喷出后，在初始段内磨料速度逐渐增大，在初始段末端，磨料速度未达到速度最大值。随后磨料进入基本段，磨料速度先增加后减小，磨料速度最大值出现在基本段内。在本例中，磨料速度与流体速度相同出现在距离喷嘴出口26.96 mm处。磨料速度最大值约为95.18 m/s,出现在距离喷嘴出口32.67 mm处，约为等速核长度的1.32倍，为喷嘴直径的8.17倍。

图4为自由磨料射流轴心磨料加速度变化趋势图，从图中可以发现，在初始段内，磨料的加速度随着距离的增加逐渐减小，而且磨料的加速度的值为是正的，意味着磨料在初始段内一直处于加速状态，这与图3中初始段内磨料速度的变化趋势是一致的。根据初始段内磨料加速度表达式，可知，流体速度保持不变，磨料速度在逐渐增加，同时由于流体速度比磨料速度大，所以流体速度与磨料速度之差在逐渐减小，而且流体速度与磨料速度之差为正。所以磨料的加速度随着磨料运动距离的增加减小，而且为正值。

图4 自由磨料射流轴心磨料加速度变化趋势图Fig.4 Trend chart of particle acceleration at the centerline of free abrasive water jet

在3.84 mm处的雷诺数等于10 002.90，而在3.85 mm处的雷诺数等于9 999.79，根据表1，可知这两处的阻力系数分别为0.41、0.42，最终使得在3.85 mm处的加速度要大于3.84 mm处的加速度。

在基本段内，磨料加速度随着磨料运动距离的增加出现了先减小后增大的过程。而且磨料加速度的值出现了正负值。根据磨料加速度表达式可知，基本段内磨料加速度由两部分构成。在基本段内，流体速度是逐渐减小的，所以(Vwi-Vwi+1)大于零，所以Vwi与(Vwi-Vwi+1)的乘积大于零，而且两者的乘积会随着磨料运动距离的增大逐渐减小。在图3中可看出，在24.8～26.96 mm之内流体速度比磨料速度大，流体速度与磨料速度之差仍然大于零。所以根据加速度的表达式可知，磨料的加速度大于零，而且加速度的值逐渐减小。因此在这段距离内，磨料速度逐渐在增加，但是增幅越来越小。

随着磨料速度的增加，流体速度与磨料速度之差小于零，并且差值逐渐增大，同时Vwi与(Vwi-Vwi+1)的乘积又在逐渐减小，直到两者之和等于零时，磨料速度达到最大值。在图4中磨料加速度在32.67 mm处等于零，此处磨料速度达到最大值。磨料达到最大值后，磨料的加速度变成小于零，所以磨料速度逐渐减小。

根据力学分析以及流体速度在初始段轴心的特性，基本段的磨料加速度比初始段内的磨料加速度多出一项，所以在基本段内，出现了加速度跃迁的现象。

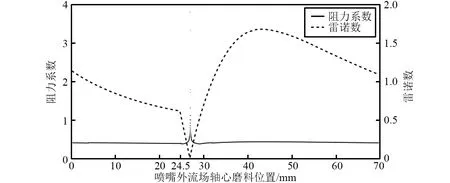
图5 自由磨料射流轴心雷诺数与阻力系数变化图Fig.5 The change of Reynolds number and drag coefficient at the centerline of free abrasive water jet

图5是磨料沿着自由磨料射流轴心运动时的雷诺数Re和阻力系数CD的变化图。初始段内，随着磨料运动距离的增加，磨料速度增大，而流体速度不变，所以流体速度与磨料速度之差的绝对值随之减小，因此雷诺数随着磨料运动距离的增加而减小。而在基本段内一定距离内，由于流体速度在减小，磨料速度在增加，所以磨料速度与流体速度之差的绝对值随之减小，雷诺数随之减小。而后流体速度和磨料速度都在减小，两者减小幅度不一致，从图中可以看出，雷诺数随着磨料运动距离的增加先增大而后逐渐减小。

从图5中可以看出，在整个过程中，阻力系数的值是一个变化值。阻力系数基本上是随着磨料运动距离的增加先增大后减小的规律。因此，在研究磨料的运动过程时，不可将阻力系数CD当做一个定值处理。

综上分析，可知自由磨料射流轴心磨料速度变化规律，即在初始段内磨料速度逐渐增大，但是磨料速度未达到速度最大值。在基本段内，磨料速度再次增加，直到达到最大值，随后，磨料速度开始逐渐减小。

5 实验验证

为了对该模型进行验证，本文利用PIV系统对喷嘴出口的磨料射流进行拍摄实验，并利用文献[26]的方法，得到了自由磨料射流轴心不同轴向位置的磨料速度。利用PIV实验测得的磨料速度与模型理论值进行对比，验证模型的正确性。

本实验是在煤矿灾害动力学与控制国家重点实验室完成的。图6为磨料射流PIV实验示意图。实验所用PIV系统由YAG New Wave双脉冲固体激光发生器、TSI630057型工业CCD相机和TSI 610034型同步控制器组成，全部购自于美国TSI公司。其中，激光发生器输出能量为240mJ/Pulse，脉冲频率15 Hz ；CCD相机测速范围为0～1 000 m/s，分辨率为1 600 ×1 000(2M)；镜头为Nikon 50 mm/F1.8，镜头尺寸：45×68×66 mm；同步器提供一对Flash Lamp和Q-switch信号，延时精度15 n。此PIV系统测速精度为±1.0%，能够满足实验需要。

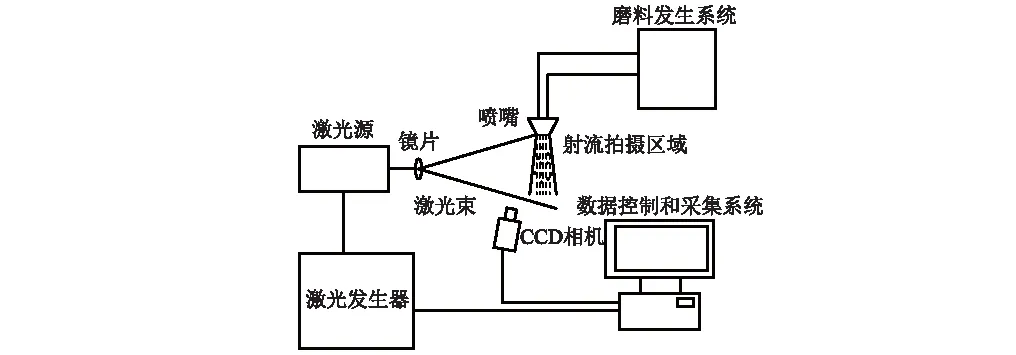
图6 磨料射流PIV实验示意图Fig.6 Schematic diagram of PIV experiments on Abrasive Water Jet

在实验中，分别对3.2 MPa下的不同喷嘴直径(3.2 mm,3.8 mm,4.5 mm)的收敛型喷嘴的磨料射流进行了PIV实验，以及对3.2 mm直径的不同泵压下(1.0 MPa,3.2 MPa,5.0 MPa)的收敛型喷嘴的磨料射流进行了PIV实验。磨料射流喷嘴出口PIV实验的实验参数设置见表2。PIV实验的拍摄范围为从喷嘴出口到距离喷嘴出口约70 mm的范围。

表2 实验参数设置Tab.2 Parameter settings for the experiment

根据参考文献[26]，计算得到喷嘴出口磨料速度的初始速度。同时等速核长度为喷嘴直径的6.2倍[10]。喷嘴出口水的速度按照经验公式(17)取值。

(17)

图7～图11为不同结构喷嘴在不同泵压下自由磨料射流轴心磨料速度理论值与实测值对比图。

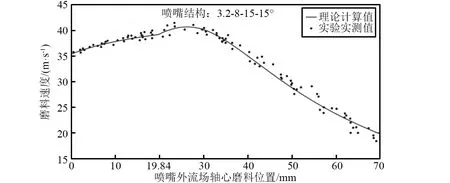
图7 1.0 MPa下3.2 mm喷嘴外流场轴心磨料速度理论值与实测值对比图Fig.7 Comparison of the measured and calculated particle velocities at the jet centerline for 3.2 mm nozzle at 1.0 MPa

图8 3.2 MPa下3.2 mm喷嘴外流场轴心磨料速度理论值与实测值对比图Fig.8 Comparison of the measured and calculated particle velocities at the centerline for 3.2 mm nozzle at 3.2 MPa

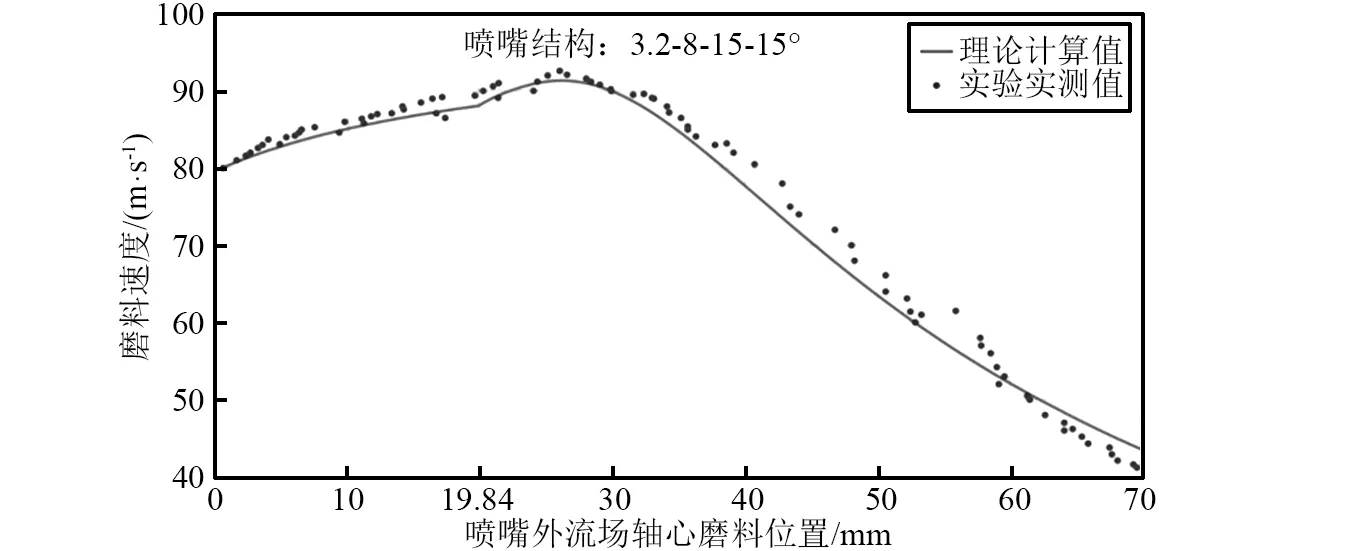
图9 5.0 MPa下3.2 mm喷嘴外流场轴心磨料速度理论值与实测值对比图Fig.9 Comparison of the measured and calculated particle velocities at the jet centerline for 3.2 mm nozzle at 5.0 MPa

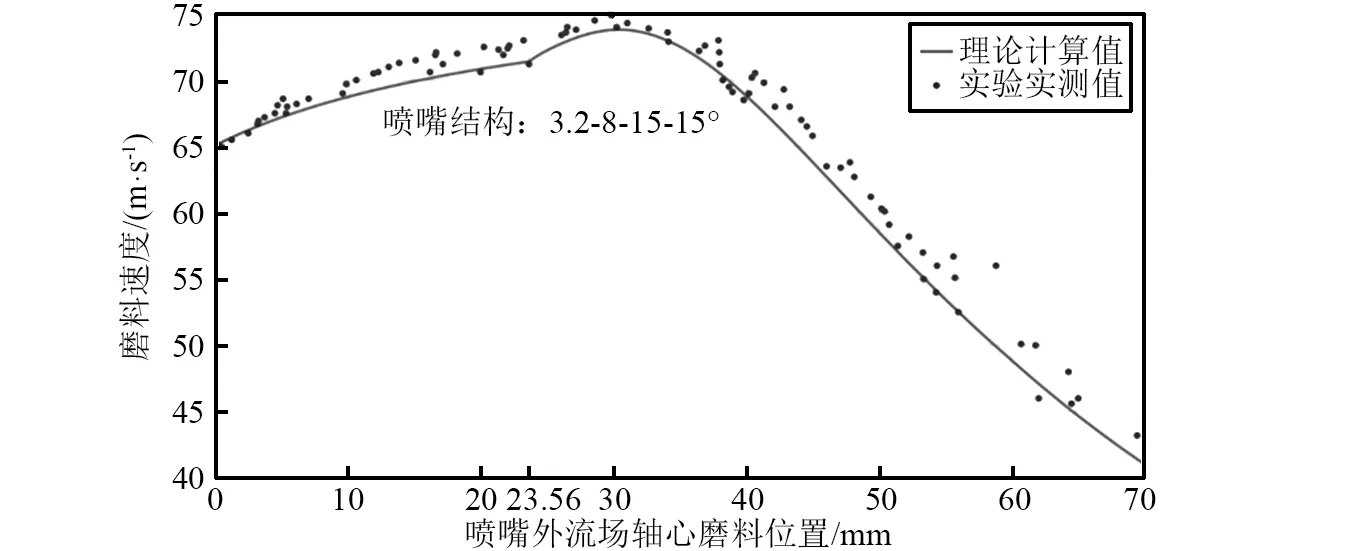
图10 3.2 MPa下3.8 mm喷嘴外流场轴心磨料速度理论值与实测值对比图Fig.10 Comparison of the measured and calculated particle velocities at the centerline for 3.8 mm nozzle at 3.2 MPa

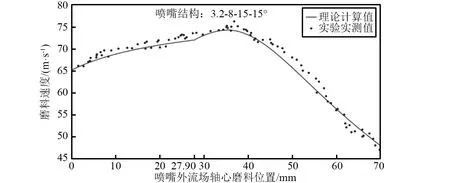
图11 3.2 MPa下4.5 mm喷嘴外流场轴心磨料速度理论值与实测值对比图Fig.11 Comparison of the measured and calculated particle velocities at the centerline for 4.5 mm nozzle at 3.2 MPa

图7～图9对应的是3.2 mm喷嘴外流场轴心磨料速度理论值与实测值对比图，从图中可以看出，压力为1.0 MPa、3.2 MPa以及5.0 MPa时，在磨料射流初始段内，即图中0～19.84 mm范围内，磨料速度实测值与理论值的变化趋势一致，都呈现出增加趋势。在基本段内，即图中19.84～70 mm范围内，磨料速度实测值与理论值的趋势都是先增大后减小的趋势。磨料速度的最大值出现在磨料射流的基本段内。

图10和图11对应的是3.2 MPa下，3.8 mm喷嘴与4.5 mm喷嘴外流场轴心磨料速度理论值与实测值对比图。从图中可以看出，对于3.8 mm喷嘴，磨料速度实测值与理论值在0～23.56 mm范围内(对应磨料射流初始段)都在增加，在23.56～70 mm范围内(对应磨料射流基本段)磨料速度实测值与理论值先增大后减小，磨料速度的最大值出现在磨料射流的基本段内。对于4.5 mm喷嘴，轴心磨料速度实测值与理论值与3.8 mm喷嘴的磨料速度变化趋势一致，磨料速度在初始段内先增加，但是速度未达到最大值，随后磨料速度在基本段内进一步增加，直至磨料速度达到最大值，而后开始减小。

从图7～图11可以看出，喷嘴外流场轴心磨料速度PIV实测值的变化趋势与理论值的变化趋势是一致的。

利用数学统计的方法对磨料速度实测值与理论值进行进一步的统计分析得到，磨料速度PIV实测值与理论值的平均百分比误差分别为2.23%，2.56%，2.32%，2.13%和1.59%。磨料速度PIV实测值与理论值的标准偏差分别为0.84 m/s，1.39 m/s，1.64 m/s，1.09 m/s和1.05 m/s。说明，磨料速度PIV实测值与理论值的大小吻合度较高，进一步对模型的正确性和准确性进行了验证。

6 结 论

(1)为了研究自由磨料射流磨料速度，本文以自由磨料射流轴心磨料为研究对象，利用自由磨料射流轴心流体速度方程及磨料运动方程，建立了自由磨料射流轴心磨料速度模型。

(2)为了求解该速度模型，提出了基于等分法和迭代算法的数值求解方法，即将磨料的运动距离等分为一定数量的线段，假设磨料在每一等分段内的运动过程中磨料加速度是一常数，利用迭代求解的方法，求出磨料的速度。

(3)自由磨料射流轴心磨料速度随着磨料运动距离的增加先增大后减小。在初始段末端磨料速度未达到速度最大值，磨料速度最大值出现在基本段内。

(4)磨料速度PIV实测值和理论值的变化趋势基本一致，实测值与理论值的平均百分比误差和标准偏差分别小于3%和2 m/s，吻合较好，验证了该速度模型的正确性和准确性。

参 考 文 献

[1] 林晓东，卢义玉，汤积仁，等.基于SPH-FEM耦合算法的磨料水射流破岩数值模拟[J].振动与冲击,2014,33(18): 170-176.

LIN Xiaodong,LU Yiyu,TANG Jiren,et al.Numerical simulation of abrasive water jet breaking rock with SPH-FEM coupling algorithm[J].Journal of Vibration and Shock, 2014,33(18): 170-176.

[2] BALZ R，MOKSO R，NARAYANAN C．Ultra-fast X-ray particle velocimetry measurements within an abrasive water jet [J] ．Experiments in Fluids, 2013, 54(3): 1476.

[3] 于鸿春.磨料射流油井割缝技术与理论的研究[D].北京：中国石油大学,2007.

[4] 林柏泉，吕有厂，李宝玉，等.高压磨料射流割缝技术及其在防突工程中的应用[J].煤炭学报,2007(9): 959-963.

LIN Baiquan, LÜ Youchang, LI Baoyu, et al.High pressure abrasive hydraulic cutting seam technology and its application in outbursts prevention [J].Journal of china Coal Society, 2007(9): 959-963.

[5] 李兆泽.磨料水射流抛光技术研究[D].长沙：国防科学技术大学,2011.

[6] LU Yiyu, TANG Jiren, GE Zhaolong, et al.Hard rock drilling technique with abrasive water jet assistance[J].International Journal of Rock Mechanics & Mining Sciences, 2013, 60(2): 47-56.

[7] KIM J G, SONG J J.Abrasive water jet cutting methods for reducing blast-induced ground vibration in tunnel excavation[J].International Journal of Rock Mechanics & Mining Sciences, 2015, 75: 147-158.

[8] NEILSON J H, GILCHRIST A.An analytical and experimental investigation of the velocities of particles entrained by the gas flow in nozzles[J].Journal of Fluid Mechanics, 1968, 33(1): 131-149.

[9] STEVENSON A N J, HUTCHINGS I M.Scaling laws for particle velocity in the gas-blast erosion test[J].Wear, 1995, 181(95): 56-62.

[10] LI H Z, WANG J, FAN J M.Analysis and modelling of particle velocities in micro-abrasive air jet[J].International Journal of Machine Tools & Manufacture, 2009, 49(11): 850-858.

[11] 王瑞和,仲冠宇,周卫东,等.基于基因表达式编程算法的磨料射流切割深度预测模型[J].中国石油大学学报(自然科学版),2015，39(1): 60-65

WANG Ruihe，ZHONG Guanyu，ZHOU Weidong，et al． A model for predicting cutting depth of casing using AWJ technique based on gene expression programming algorithm[J].Journal of China University of Petroleum(Edition of Natural Science),2015,39( 1) : 60-65．.

[12] 董星,马安昌,吴财芳,等.基于神经网络的前混合磨料射流切割深度的研究[J].煤炭学报,2002(4): 430-433.

DONG Xing, MA Anchang, WU Caifang, et al.Neural network method and the study of the cut depth of DIA jet[J].Journal of China Coal Society, 2002(4): 430-433.

[13] 周卫东,王瑞和,杨永印,等.前混式磨料水射流切割套管的深度计算模型[J].石油大学学报(自然科学版),2001(2): 3-5+11.

ZHOU Weidong, WANG Ruihe, YANG Yongyin, et al.Models for calculating cutting depth of casing by premixing abrasive water jet[J].Journal of the University of Petroleum China, 2001(2): 3-5.

[14] 汤积仁,卢义玉,孙惠娟,等.基于CT方法的磨料射流冲蚀损伤岩石特性研究[J].岩石力学与工程学报,2016(2): 297-302.

TANG Jiren, LU Yiyu,SUN Huijuan, et al.Study of erosion and damage characteristics of rock by abrasive water jet using CT[J].Chinese Journal of Rock Mechanics and Engineering, 2016(2): 297-302.

[15] 沈忠厚．水射流理论与技术[M]．东营: 石油大学出版社, 1998：293-327.

[16] 李晓红, 卢义玉, 向文英, 等.水射流理论及在矿业工程中的应用[M].重庆：重庆大学出版社, 2007：39-40.

[17] RAJARATNAM N.Turbulent Jets[J].Developments in Water Science, 1976, 76(5): 77-82.

[18] BOGUSLAWSKI L, CO P.Flow structure of the free round turbulent jet in the initial region[J].Journal of Fluid Mechanics, 1979, 90 (3): 531-539.

[19] ABRMOVICH G, SCHINDEL L.General properties of turbulent jets[M].MIT press, 1963.

[20] ALBERTSON M L, DAI Y B, JENSEN R A, et al.Diffusion of submerged jets[J].Transactions of the American Society of Civil Engineers, 1950, 115(1): 639-664.

[21] CROW S C, CHAMPAGNE F H.Orderly structure in jet turbulence[J].Journal of Fluid Mechanics, 1971, 48(3): 547-591.

[22] BUSH W B, KRISHNAMURTHY L.Asymptotic analysis of the fully developed region of an incom-pressible, free, turbulent, round jet[J].Journal of Fluid Mechanics, 1991, 223: 93-111.

[23] 王明波，王瑞和.喷嘴内液固两相射流流场的数值模拟[J].石油大学学报(自然科学版) ,2005(5): 46-49.

WANG Mingbo,WANG Ruihe.Numerical simulation on fluid-particle two-phase jet flow field in nozzle[J] ．Journal of the University of Petroleum , China，2005(5)：46-49．

[24] MORIS S A, ALEXANDER A J.An investigation of particle trajectories in two phase flow system[J].J.Fluid Mech., 1972, 55(2): 193-208.

[25] 左伟芹, 王晓川, 郝富昌,等.基于迭代算法的磨料颗粒加速机制研究[J].中国石油大学学报(自然科学版), 2016, 40(4):104-109.

ZUO Weiqin,WANG Xiaochuan,HAO Fuchang, et al.Research on acceleration mechanism of abrasive in pre-mixed abrasive water-jet based on iterative algorithm[J].Journal of China University of Petroleum(Edition of Natural Sciences), 2016, 40(4):104-109.

[26] 章文峰,卢义玉,汤积仁,等.基于PIV技术的磨料水射流中固体磨料粒子速度分布实验研究[J].振动与冲击,2016,35(8): 159-165.

ZHANG Wenfeng，LU Yiyu，TANG Jiren,et al.Experimental study of velocity distribution of solid abrasive particles in abrasive water jets based on PIV technology[J].Journal of Vibration and Shock, 2016,35(8): 159-165.