考虑液化场地流变效应的地下结构侧向作用力研究
2016-11-23周恩全
左 熹, 周恩全, 任 艳
(1.金陵科技学院 建筑工程学院,南京 211169;2.南京工业大学 岩土工程研究所,南京 210009;3.江苏大学 土木工程与力学学院,江苏 镇江 212013)
考虑液化场地流变效应的地下结构侧向作用力研究
左 熹1,2, 周恩全3, 任 艳2
(1.金陵科技学院 建筑工程学院,南京 211169;2.南京工业大学 岩土工程研究所,南京 210009;3.江苏大学 土木工程与力学学院,江苏 镇江 212013)
将液化流动的土体视为流体,基于流体力学原理,运用矢量法进行液化速度场的分析,并通过矢量符号运算法求解速度场,得出地下结构在液化流动场地中受到侧向作用力的解析表达式,并对解析表达式中的参数进行灵敏度分析。结果表明:在液化土体横向流动时,地下结构所受侧向作用力既包含表面压力引起的压力阻力,又包含剪应力引起的摩擦阻力。侧向作用力主要由惯性力和阻尼力组成,并与流体密度、流体黏度、地下隧道半径及结构振动频率有关。随着流体密度、流体黏度、隧道半径的增大,附加质量和附加阻尼均逐渐增加;在一定范围内,附加质量和附加阻尼对振动频率较为敏感。
流变效应;液化场地;地下结构;侧向作用力
自1995年日本阪神地震对神户市地铁车站及区间隧道产生严重震害,由此可液化场地对地下结构的作用效应问题得到越来越高度的重视[1]。由于液化后土体的力学特性与固体有显著差异,并表现出低抗剪性、高流动性等流体性质,因此将液化后土体视为流体,考虑流变效应来研究液化土体与结构的相互作用。TOWHATA等[2]首次将液化土体视为流体来研究液化土体的侧向大变形,自此考虑液化土体的流变效应受到了学者的普遍关注。
不同学者对液化场地流变效应的研究不尽相同,UZUOKA等[3]将液化土体视为流体,采用压力耦合方程的半隐式算法求解Navier-Stokers方程,以此得出液化土体对挡土结构的侧向作用力。HWANG等[4]将液化后的砂土作为一种流体,利用Flow3D软件分析不同深度处土层的流体黏度特性,进一步运用ABAQUS/AQUA软件分析单桩在倾斜液化场地的反应。MONSTASSAR等[5]基于最小势能原理研究液化后砂土的流动变形,并分析了液化后砂土对桩基的影响。SAWICKI等[6]利用流体力学中经典平衡方程Navier-Stokes公式来研究液化砂土的沉降以及流滑。HUANG等[7]提出一种计算流体动力学方法进行液化土体流动行为的数值模拟,并证明了所提出的方法能够被用于再现液化后土体的流动行为。JAFARIAN等[8]将液化的土体作为一种黏性流体,使用计算流体力学预测无限土坡液化引起的侧向变形,并采用离心模型试验和数值模拟进行了验证。MIAO等[9]提出在土体液化小变形的初始阶段,采用基于固体力学的有限元可以准确模拟土体行为;但在液化变形的流动阶段,流体动力学SPH方法更合适,因为土体在流动阶段的特性与黏性流体尤为相似。
本文将液化流动的土体视为流体,基于流体力学原理,运用矢量法进行液化速度场的分析,并通过矢量符号运算法求解速度场,得出了考虑液化场地流变效应的地下结构侧向作用力解析表达式,由此得知液化场地对地下结构的侧向作用力主要由惯性力和阻尼力组成,并与流体密度、流体黏度、隧道结构半径及振动频率有关,最后针对解析解中的参数进行灵敏度分析,得出不同参数的敏感程度。
1 考虑地下结构效应液化场地的速度分布场
1.1 基于矢量分析法的速度场分析
在土体液化过程中,由于孔隙水压力的增大和有效应力的减小,导致土体由固体状态转变为液体状态[10],因此,引入流体力学的观点,可得出考虑地下结构效应液化场地的速度分布场,如图1。
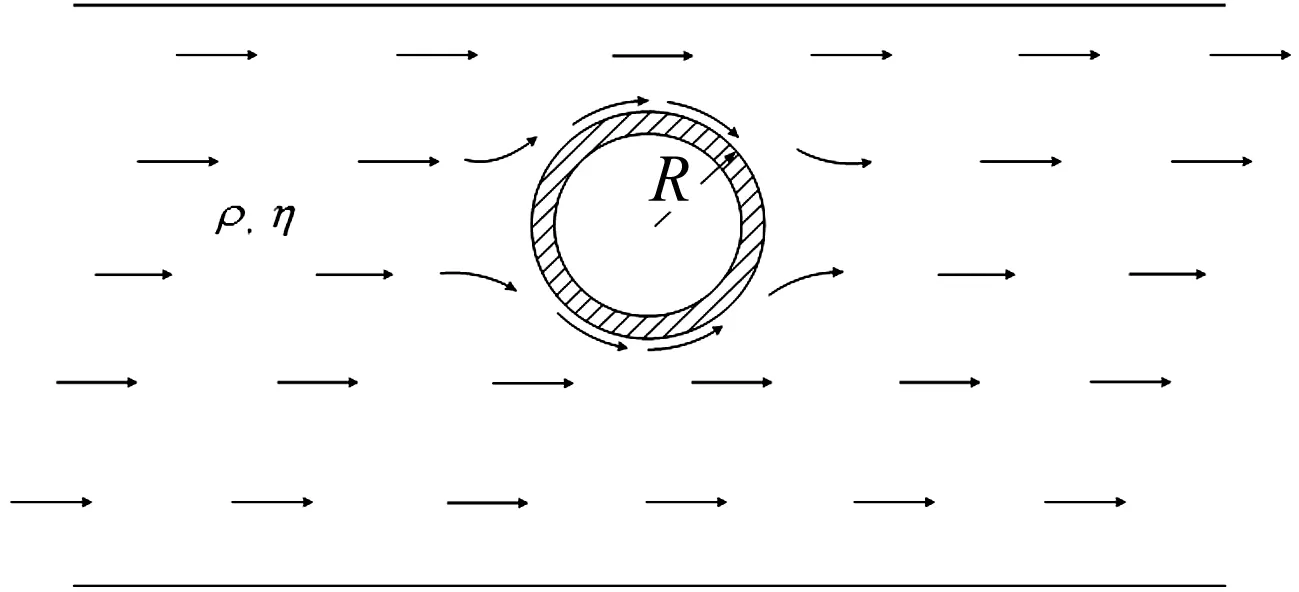
图1 液化场地的速度分布场示意图Fig.1 Schematic diagram of velocity field of liquefaction field
设圆形地下隧道结构的截面半径为R,土体发生液化流动状态时的密度为ρ,黏度为η。地下隧道结构在液化流动场中的运动速度为v=v0e-iωt,其中ω为隧道结构的振动频率;v0表示地下结构在土体液化初始时刻的速度,为常矢量。假设在土体液化流动为无限远来流,当其速度为v0时,对隧道结构的侧向绕流速度场为V′0;隧道结构运动引起的液化场地的流动速度场为V0,则有:V′0=V0+v0。
将液化流动的土体理解为不可压缩流体,根据连续方程,可得:
V′0=(V0+v0)=V0=0
(1)
根据矢量理论,极矢量V0对应存在轴矢量A,使(×A)=0成立,故可得:
V0=×A
(2)
式中:A是轴矢量,可表示为两个极矢量的矢积,由于A只与极矢量矢径γ和速度v0有关,所以A一定由γ×v0构成,并且γ可由函数f(x)的梯度f′(r)n表示,对于地下隧道这种细长结构,可认为A与轴向位置坐标z无关,即A具有为f′(r)nv0的矢积形式,另外由于f′(r)n=f,且v0是常矢量,则
V0=(f×v0)
(3)
因此,地下结构以速度v=v0e-iωt在流体场中振动引起的速度场为:
V=[(f×v0)]e-iωt
(4)
1.2 运用矢量符号运算法求解速度场
由于液化的土体属于不可压缩流体,由动量方程可得:
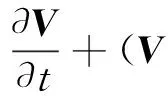
(5)
式中:η为液化土体流动状态的流体黏度,ρ为液化土体流动状态的流体密度,P为地下结构周围的应力场。
由于土体液化引起的流体运动属于一种低雷诺数的均匀流[11],故公式中的惯性项(V)V可以忽略,得到线性化的N-S方程:
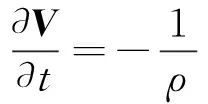
(6)
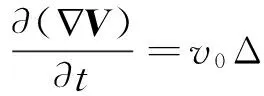
(7)
将式(4)代入式(7),运用矢量符号运算得到:
[v0Δ2f+iωΔf]=0
(8)
则有:
v0Δ2f+iωΔf=Constant
(9)
由无限远处边界条件可知,Constant=0,因此:
v0Δ2f+iωΔf=0
(10)
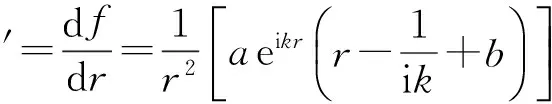
在柱坐标系下采用矢量符号运算法可得速度场:
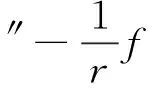
(11)
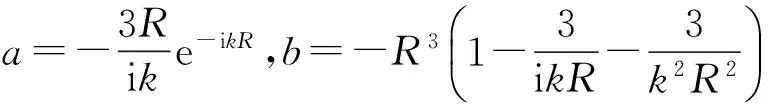
由式(11)知,V0在法向、切向、轴向的分量分别为:
(12)
V0θ=f″v0sinθ
(13)
V0z=0
(14)
2 地下结构的围压应力场
由于流动的液化土属于黏性不可压缩流体,并且在小雷诺数情况下,根据Navier-Stokes方程有:
ηΔV-p=0
(15)
根据应力张量公式[12],黏性不可压缩流体中的应力张量(柱坐标下)可表达为:
(16)
(17)
(18)
(19)
(20)
(21)
将式(3)、(4)、(12)~(14)代入(15),可得到:
[ηΔ(fv0)+iωρfv0]
(22)
对式(22)积分可得到地下隧道结构周围压力分布为:
P0=ηΔ(fv0)+iωρfv0+P∞=
iωρv0f′cosθ+P∞
(23)
将式(12)~(14)代入式(16)~(21)可得圆形地下隧道结构周围应力张量的分布为:
(24)
(25)
(26)
(27)
(28)
(29)
根据地下隧道结构周围应力张量的计算结果,可以发现:液化土体横向流动时,地下隧道结构既受到由表面压力引起的压力阻力,又受到由剪应力引起的摩擦阻力。
地下隧道结构所受到的侧向作用力与土体液化流动的速度平行,故将作用在圆形隧道表面上的所有面力向流体速度方向投影,并沿整个隧道的圆柱面积分,可得到作用在单位长度圆形地下隧道结构的侧向作用力为:
(30)
在隧道结构圆柱面上,r=R,有:
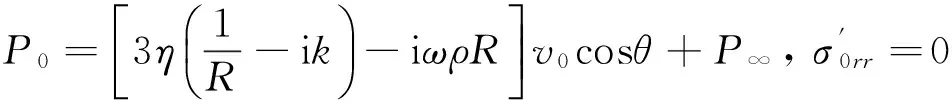
(31)
式中:η为液化土体流动状态的流体黏度,ρ为液化土体流动状态的流体密度,R为隧道结构的半径,ω为隧道结构的振动频率。
由式(31)可知,液化场地对地下结构的侧向作用力主要由惯性力和阻尼力组成,并且其动力特性与流体密度、流体黏度、地下隧道半径及地下结构的振动频率有关。可令:
(32)
(33)
式中:ma为地下隧道结构的动力附加质量,ca为地下隧道结构的动力附加阻尼,二者分别反映了地下结构在液化流动场地中横向振动时的动力学特性。
最终,液化场地对地下结构的侧向作用力可表示为:
(34)
3 参数灵敏度分析
3.1 灵敏度分析方法
定义灵敏度指标为函数相对于某个参数的导数,即在某个参数点xi处,动力附加质量函数M(X)或动力附加阻尼C(X)对xi的灵敏度为:
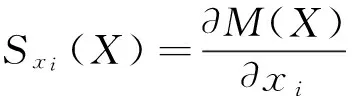
(35)
式中:Sxi反映了函数M(X)或C(X)对参数xi的单调性。Sxi绝对值的大小表示各函数对参数xi的敏感程度,该值越大,表示函数对xi越敏感。
以下对流体密度、流体黏度、地下隧道半径及地下结构的振动频率的灵敏度进行分析,采用的模型及参数参考值为:液化土体采用牛顿流体模型,流动土体密度ρ=1 800 kg/m3,流体黏度η=103Pa·s;地下隧道结构采用弹性模型,隧道半径R=3 m,地下结构振动频率ω=2 Hz,在各参数的敏感度分析过程中,基于单一参数变化,其它参数保持不变。边界条件为无限边界。
3.2 流动土体密度
附加质量和附加阻尼随流动土体密度的变化曲线如图2所示,可以看出:附加质量和附加阻尼随着流体密度的增大而增加,说明随着流体密度的增大,液化土体对地下结构的侧向作用力逐渐增大。灵敏度随着流体密度的增大而减少,表明流体密度越小,对侧向作用力越敏感;附加阻尼对应的灵敏度变化幅度明显大于附加质量对应的灵敏度,证明了流体密度对附加阻尼的影响更大。
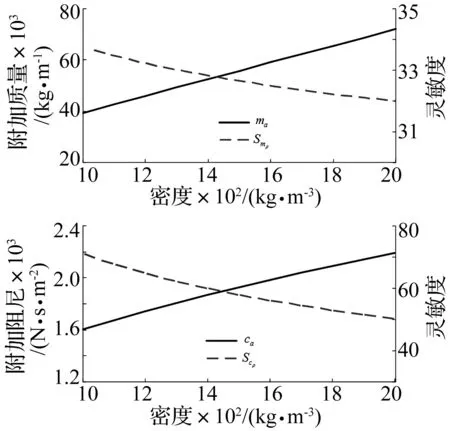
图2 流体密度对附加质量和附加阻尼的影响Fig.2 Influence of fluid density on the additive mass and additive damping
3.3 流动土体黏度
附加质量和附加阻尼随流动土体黏度的变化曲线如图3所示,可以发现:附加质量和附加阻尼均随着流体黏度的增大而增加;灵敏度随着流体黏度的增大而减少,说明流体黏度越小,对侧向作用力越敏感,并且当流体黏度处于1 000 Pa·s~2 000 Pa·s时,对应的灵敏度急剧下降,说明在此区间内,流体黏度的变化对侧向作用力的影响较大。附加阻尼对应灵敏度的变化幅度更大,说明流体黏度对附加阻尼的影响更大。
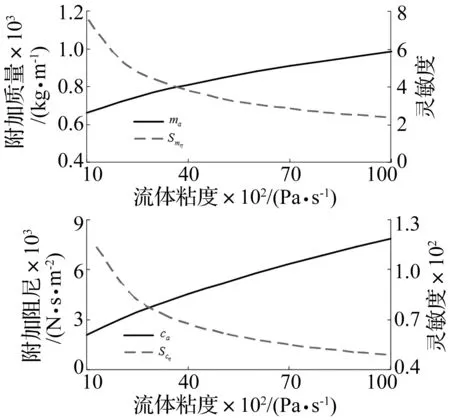
图3 流体黏度对附加质量和附加阻尼的影响Fig.3 Influence of fluid viscosity on the additive mass and additive damping
3.4 地下隧道半径
附加质量和附加阻尼随地下隧道半径的变化曲线如图4所示,可以发现:随着隧道半径的增大,附加质量和附加阻尼均逐渐增加,其中附加质量对应的灵敏度随之增大,而附加阻尼对应的灵敏度保持不变,说明隧道半径对附加质量有一定的敏感性,但对附加阻尼不敏感。这是因为在侧向流动的液化场地中圆形隧道结构更利于阻力耗散,导致隧道半径对附加阻尼不敏感。
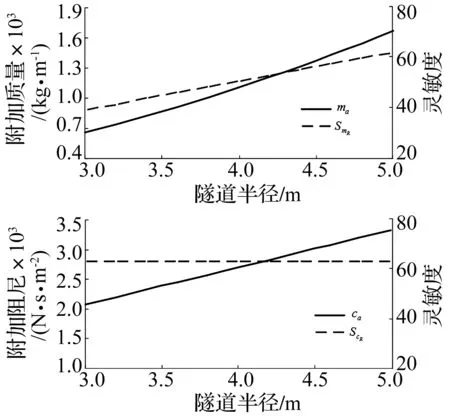
图4 隧道半径对附加质量和附加阻尼的影响Fig.4 Influence of tunnel radius on the additive mass and additive damping
3.5 地下结构振动频率
附加质量和附加阻尼随地下隧道振动频率的变化曲线如图5所示,可以看出:随着振动频率的增大,附加质量急剧减小并逐渐趋于稳定,附加阻尼逐渐增加,附加质量和附加阻尼对应的灵敏度均表现出低频阶段迅速减小,并趋于一个较小值,说明当频率小于1 Hz时,振动频率对侧向作用力尤为敏感。这是由于当地下隧道结构处于一定频率范围内,此时与液化场地的自振频率接近,由此产生共振效应,导致对附加质量和附加阻尼的灵敏度显著提高。
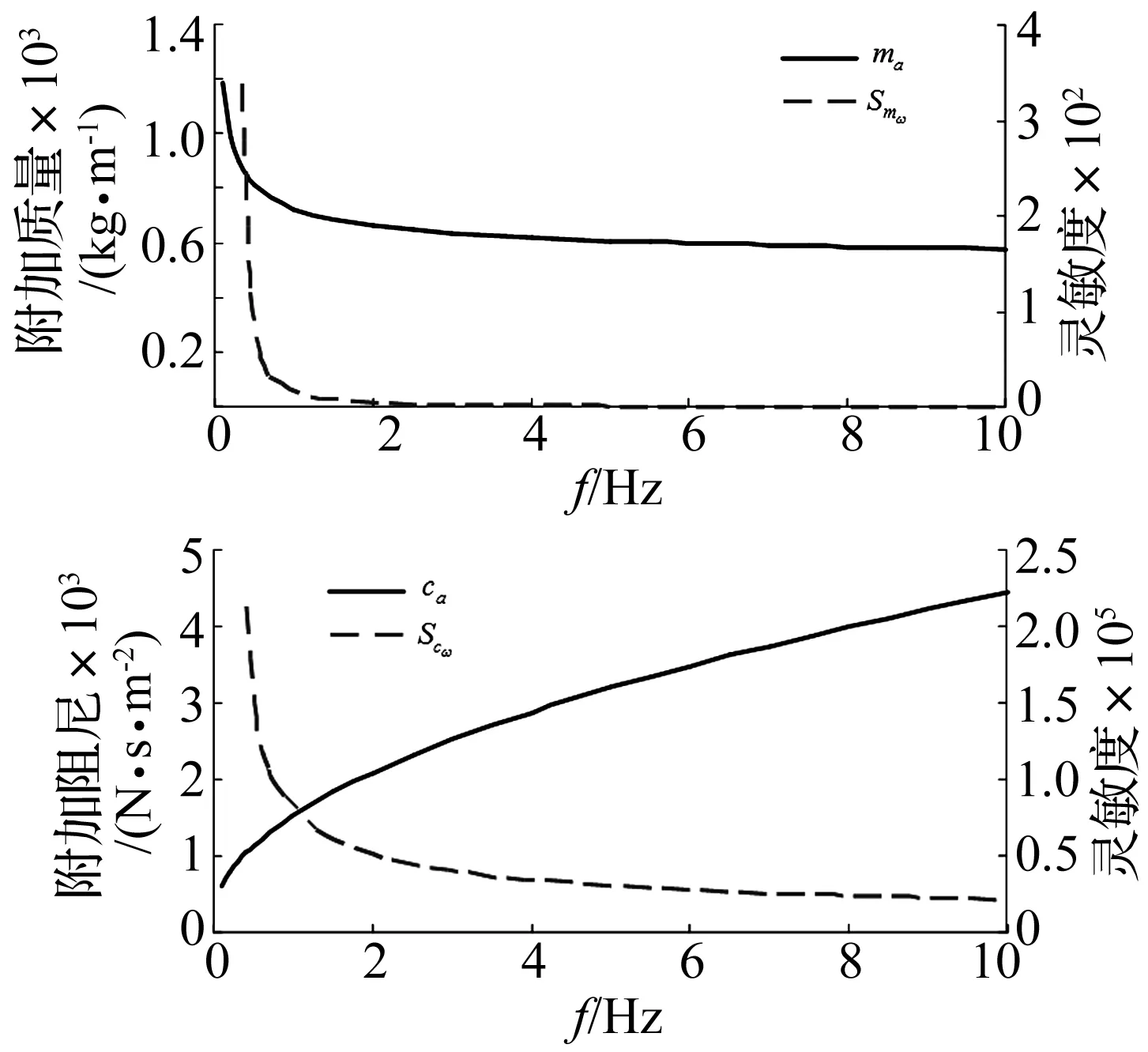
图5 振动频率对附加质量和附加阻尼的影响Fig.5 Influence of vibration frequency on the additive mass and additive damping
4 结 论
将液化流动的土体视为流体,运用流体力学原理,基于矢量法进行液化场地的速度场分析,并运用矢量符号运算法求解速度场,得出考虑液化场地流变效应的地下结构侧向作用力解析表达式,对解析解中的参数进行了灵敏度分析,得出不同参数对地下结构侧向作用力的影响。主要结论如下:
(1) 根据地下隧道结构周围应力张量的计算结果,可知在液化土体横向流动时,地下隧道结构既受到由表面压力引起的压力阻力,又受到由剪应力引起的摩擦阻力。
(2) 液化场地对地下结构的侧向作用力主要由附加惯性和附加阻尼组成,与流体密度、流体黏度、地下隧道半径及地下结构的振动频率有关。
(3) 随着流体密度、流体黏度、隧道半径的增大,附加质量和附加阻尼均逐渐增加,相对附加质量而言,流体密度、流体黏度对附加阻尼的影响更大,而隧道半径仅对附加质量有一定的敏感性;在一定范围内,附加质量和附加阻尼对振动频率较为敏感。
[1] 王国波, 谢伟平, 孙明, 等. 地下框架结构抗震性能评价方法的研究[J]. 岩土工程学报, 2011, 33(4): 593-598.
WANG Guobo, XIE Weiping, SUN Ming,et al. Evaluation method for seismic behaviors of underground frame structures[J]. Chinese Journal of Geotechnical Engineering,2011,33(4): 593-598.
[2] TOWHATA I, YSSUDA S, KEN-ICHI T, et al. Prediction of permanent displacement of liquefied ground by means of minimum energy principle[J]. Soils and Foundations,1992, 32(3): 97-116.
[3] UZUOKA R, YASHIMA A, KAWAKAMI T, et al. Fluid dynamics based prediction of liquefaction induced lateral spreading[J]. Computers and Geotechnics,1998, 22(3): 243-282.
[4] HWANG J, KIM C, CHUNG C, et al. Viscous fluid characteristics of liquefied soils and behavior of piles subjected to flow of liquefied soils[J]. Soil Dynamics and Earthquake Engineering,2006, 26(2/3/4): 313-323.
[5] MONTASSAR S, DE BUHAN P. A numerical model to investigate the effects of propagating liquefied soils on structures[J]. Computers and Geotechnics,2006, 33(2): 108-120.
[6] SAWICKI A, MIERCZYSKi J. On the behaviour of liquefied soil[J]. Computers and Geotechnics,2009,36(4): 531-536.
[7] HUANG Yu,MAO Wuwei,ZHENG Hu, et al. Computational fluid dynamics modeling of post-liquefaction soil flow using the volume of fluid method[J]. Bulletin of Engineering Geology and the Environment, 2012, 71(2): 359-366
[8] JAFARIAN Y,GHORBANI A,AHMADI O. Evaluating liquefaction-induced lateral deformation of earth slopes using computational fluid dynamics (CFD)[C]//15th World Conference on Earthquake Engineering, Lisbon, Portugal,2012.
[9] MIAO Yu, HUANG Yu, XU Qiang. Numerical methods for deformation analysis of liquefiable soils[J]. Engineering Geology for Society and Territory, 2014, 4(1): 55-57
[10] 王志华, 周恩全, 陈国兴, 等. 循环荷载下饱和砂土固-液相变特征[J]. 岩土工程学报, 2012, 34(9):1604-1610.
WANG Zhihua, ZHOU Enquan, CHEN Guoxing,et al. Characteristics of solid-liquid phase change of saturated sand under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(9): 1604-1610.
[11] 陈育民, 刘汉龙, 邵国建, 等. 砂土液化及液化后流动特性试验研究[J]. 岩土工程学报, 2009, 31(9): 1408-1413.
CHEN Yumin, LIU Hanlong, SHAO Guojian,et al. Laboratory tests on flow characteristics of liquefied and post-liquefied sand[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(9): 1408-1413.
[12] (苏) 朗道(Ландау,Л.Д.), (苏) 栗弗席茨(Лифщиц,Е.М.)著,孔祥言等译.流体力学[M]. 北京:高等教育出版社, 1990.
Lateral force of underground structures considering rheological effect of liquefied
ZUO Xi1,2, ZHOU Enquan3, REN Yan2
(1. Institute of Architectural Engineering, Jinling institute of technology, Nanjing 211169, China;2. Institute of Geotechnical Engineering, Nanjing University of Technology, Nanjing 210009, China;3. Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China)
Regarding liquefied soil as fluid and using the vector method to analyze liquefaction velocity field based on the principle of fluid mechanics, the liquefaction velocity field was solved with the vector symbolic operation method. Thus, the analytical expression of lateral forces of underground structures in the liquefaction flow site was obtained. The parameter sensitivity of the analytical expression was analyzed. The results showed that the lateral force of underground structures contains both pressure resistance due to surface pressure and friction resistance due to shear stress; lateral force is mainly composed of inertial force and damping force, and it is related to fluid density, fluid viscosity, underground tunnel radius and vibration frequency of structures; with increase in fluid density, fluid viscosity and tunnel radius, added mass and added damping increase gradually; within a certain range, added mass and added damping are more sensitive to vibration frequency.
rheological effect; liquefied soils; underground structure; lateral force
国家自然科学基金(51408281);中国博士后科学基金(2013M540442);江苏省自然科学基金(BK20140108;BK20141090)
2015-03-17 修改稿收到日期:2015-09-05
左熹 男,博士,副教授,1982年11月生
TU432;TU93
A
10.13465/j.cnki.jvs.2016.19.010
