高等数学中一元函数几类常用极限求法实例探析

黔南民族师范学院数学系 向 彪

高等数学中一元函数几类常用极限求法实例探析

黔南民族师范学院数学系 向 彪①

函数极限的求法是高等数学学习的难点问题之一，也是全国研究生入学考试公共数学科目必考的内容。求极限的方法较多，本文总结出了几种常用的求极限的方法，并给出了几道考研真题实例，希望对考研的同学有一定的帮助。

极限；洛必达法则；实例

极限贯穿高等数学始终，极限的求法是高等数学学习的难点问题之一。在实际解题过程中，函数极限的求法是多种多样的，同学们在学习过程中，往往对求极限的方法难以选择，不知道用哪种方法好，因此，分析和研究函数极限的求法，是非常有必要的。求极限的方法种类繁多，本文有针对性地研究讨论了几种在实际计算中用得较多、考研真题中出现较多的几种。

一、函数极限的定义

设函数f（x）在点的某一去心邻域内有定义。如果存在常数A，对任意给定的正数ε（无论ε它有多小），总存在正数δ，使得当x满足时，对应的函数值都成立，则称A为函数f（x）当x→x0时的极限，记作：恒有：。

二、函数极限求法例析

1.利用两个重要极限求极限

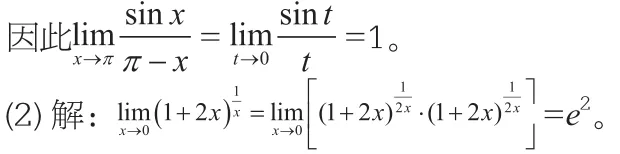
2.利用两边夹原理求极限

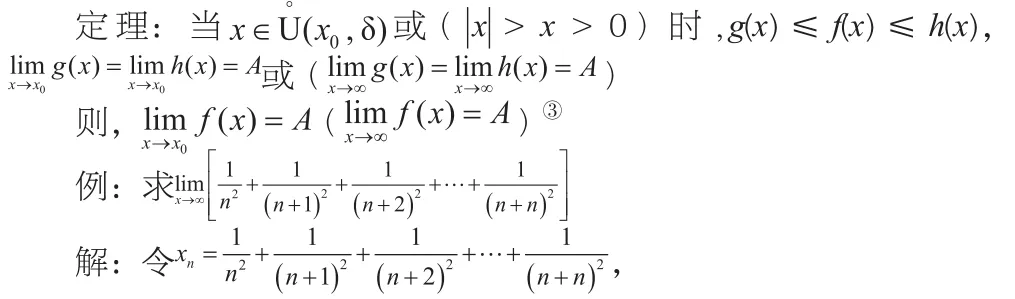
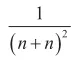
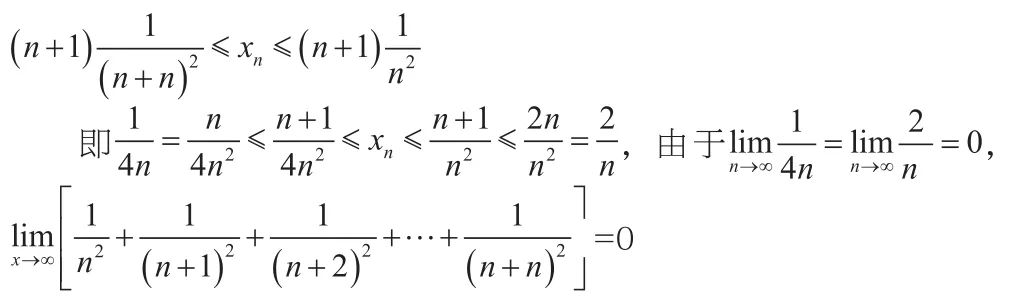
3.等价无穷小代换求极限

注意：求两个无穷小之商的极限时，分子与分母都可用等价无穷小来代替，乘法项可直接代替，加减法项不可直接代替，加减项只能整体代换！

4.利用洛必达法则求极限

5.利用麦克劳林展开式求极限

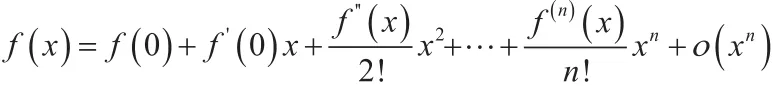
三、考研真题分析

在实际解题过程中，尤其是在研究生入学统一考试数学题目中，求极限绝不会局限于使用某一种方法，都是几种方法结合在一起使用的，灵活度较高，这就要求我们在具体的解题过程中思维开阔，不钻死胡同，灵活运用，下面举几个考研的例题来说明。

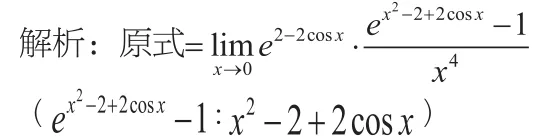
（此步骤，使用了等价无穷小替换方法，学生必须牢记常用的几种等价无穷小，才能熟练使用这一方法。）

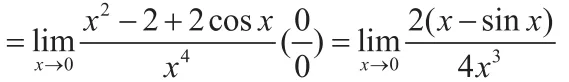
（此步骤，使用罗比达法则）

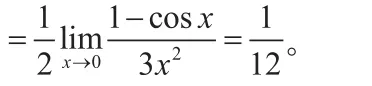
［1］同济大学数学系.高等数学（上下册，第七版）［M］.北京：高等教育出版社，2014.

［2］华东师范大学数学系.数学分析［M］.北京：高等教育出版社，2001.

［3］陈文灯.数学复习指南［M］.北京：世界图书出版社，2014.

①向彪（1982-），男，贵州江口人，硕士，黔南民族师范学院讲师，研究方向：基础数学。

②同济大学数学系.高等数学（上册，第七版）19页

③同济大学数学系.高等数学（上册，第七版）27页

④同济大学数学系.高等数学（上下册，第七版）187页