分式的意义在中考中的考向与应对策略
2016-11-17四川省安岳县九龙乡九年义务教育学校龚交完
四川省安岳县九龙乡九年义务教育学校 龚交完
分式的意义在中考中的考向与应对策略
四川省安岳县九龙乡九年义务教育学校龚交完
分式的意义是初中数学的重点内容之一,也是中考考查座上客。纵观近年来的中考试题中,其主要考查的方式有三类:第一类是分式中字母的取值与分式的关系;第二类是分式中字母取什么值时分式的值为零;第三类是分式中字母取什么值时分式的值不为零。只有明确了在中考中分式的意义如何考,才能找到解决问题的应对策略。本文就是谈谈分式的意义在中考中的考向及应对策略,以供与中考备考有关的师生参考。
分式的意义;考向;应对策略
一、分式中字母的取值与分式的关系
要明确一个代数式是分式而不是分数,就必须明确分式的概念。用A、B表示两个整式,在B中必须含有字母,这时式子称作分式。同分数一样,A叫作分子,B叫作分母,B不能为0才有意义。
这类题型要注重抓住基点:第一,一个分式表示两个整式相除,同分数一样,其中分子是被除式,而分母是除式。如可以表示(a-b)÷(c+d)。第三,作为分式的分母的除数,不能为0,当分母为0时,就分式没有意义了。第四,判断代数式是否属于分式,不能把原式经过约分等变形后再看,必须以其的本来面目进行判断,如,不能因为其变形结果a+b是整式而判定,因的分母含字母而判断其为分式。
二、分式中字母取什么值时分式的值为零
作为分式来说,要使得其值为0,就必须使得分子为0,即被除数为0;同时分式还要有意义,这就必须分母不能为0。这类问题也普遍在中考试题中出现。
A.-1B.0C.±1D.1
【考向分析】要使得一个分式的值为0时,首先必须分式有意义,即分母不等于0,然后在考虑其分子必须等于0。
对本题要点的最好诠释有以下几点,第一,分母不为0是分式概念必要条件,同分数一样分式的分母为0是没有意义的。第二,分式分母的值不为0,是指整个分母的值不为0。这与分母中的字母的值是否为0无关,只要整个分母不为0,分式还是有意义的。第三,分式的值为0,是在分式有意义的前提下,再满足分子的值为0。最重要的一点是假若没有特别说明,试题中的所有分式都是有意义的。
三、分式中字母取什么值时分式的值不为零
一个分式的值不为0,其分子必定不能为0,即被除数为0;同时分式还要有意义,这就必须分母也不能为0。这类问题成为了在中考试题的热点。
A.x≠-2B.x≠±2C.x≠2D.x≠0
【考向分析】分式的值不为0,注意不仅仅是将分式的分子不能为0,即x2-4=0,而且要使分式有意义,其分母也不能为0,即x+2≠0,所以,x≠±2,选B。

四、分式的化简
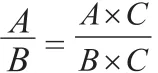
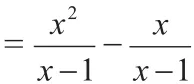
本题考查的是分式的加减法,把两个分母不相同的分式化成分母相同的分式,进行通分,经过通分,异分母分式的加减就转化为同分母分式的加减。
总之,分式的本质特征就是代数式的分母中含有字母,这是区别整式的特征。从以上四个方面可以发现,分式是分母中一定含有字母的代数式,作为分式只有是分母不为零才具有实际意义。
[1]王涛.有关分式中考试题的考点分析[J].中学生数理化(教与学),2012(8).
[2]何晶华.中考考点——分式类试题赏析[J].中学生数理化(教与学),2012(9).
[3]刘玉东.中考分式考点透析[J].数学大世界(初一二辅导),2004(11):37-38.
