V-苯烯纳米管的逆基于度的拓扑指数
2020-09-15穆罕默德纳迪姆
穆罕默德·纳迪姆
(民哈吉大学 数学系,拉合尔54000)
In mathematical chemistry, the tools of mathematics, for example, polynomials and topological index help researchers to know properties of nanotubes without experiments. These mathematical tools depend on the symmetry of graphs of nanotubes[1-2]. It is a well-known fact that most of the properties of nanotubes, for example, heat of formation, boiling point, strain energy, rigidity and fracture toughness of a nanotube are directly connected to its graphical representation and this fact plays a very important role in chemical graph theory.
Many algebraic polynomials have useful applications in the field of chemistry, for instant, Hosoya polynomial help researchers to determine distance-based topological indices. Another algebraic polynomials is the M-polynomial[3], that was introduced in year 2015 have same role as that of Hosoya polynomial for degree-based topological indices[4-5].
The first topological index was introduced by Wiener[6]and it was named path number, which is now known as Wiener index. After the success of Wiener index, a series of topological indcies has been defined. Due to need of new indices as described in abstract of this paper, reverse first and second Zagreb indices has been defined in [7]. In this paper, we defined reverse modified second Zagreb index, reverse symmetric division index, reverse harmonic index and reverse inverse sum index. Moreover we computed above mentioned topological indices for V-Phenylenic Nanotubes.
1 Definitions
In this section, we give some definitions of reverse degree-based topological indices.
Definition1(Reverse First Zagreb Index)
For a connected simple graphG, the reverse first Zagreb index is defined as:
Definition2(Reverse Second Zagreb Index)
For a connected simple graphG, the reverse second Zagreb index is defined as:
Definition3(Reverse Second Modified Zagreb Index)
For a connected simple graphG, the reverse second modified Zagreb index is defined as:
Definition4(Reverse Symmetric Division Index)
For a connected simple graphG, the reverse Symmetric division index is defined as:
Definition5(Reverse Harmonic Index)
For a connected simple graphG, the reverse Harmonic index is defined as:
Definition6(Reverse Inverse Sum-Index)
For a connected simple graphG, the reverse Inverse Sum-index is defined as:

2 Main Results
The molecular graph of V-Pheylenic Nanotube is given in Figure 1.
The edge partition of V-Pheylenic Nanotube based on the degree of end vertices is given in Table 1.
The reverse degree based edge partition of V-Pheylenic Nanotube is given in Table 2, where
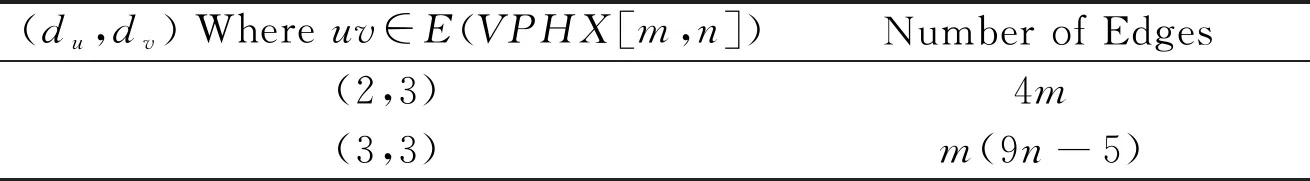
Table 1 Degree based edge partition of V-Pheylenic Nanotube

Table 2 Reverse degree based edge division of V-Pheylenic Nanotube
cv=△(G)-dv+1 and △(G) is the maximum degree of the graph.
Theorem1LetVPHX[m,n] be V-Pheylenic Nanotube. Then
CM(VPHX[m,n],x,y)=4mx2y+9mnxy-5mxy.
ProofBy using the definition of reverse first Zagreb index and reverse edge partition of V-Phenylenic Nanotube given in Table 2, we have
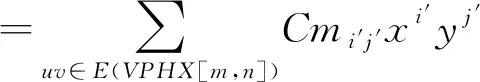
=|CE1(VPHX[m,n])|x2y1+|CE2(VPHX[m,n])|x1y1
=(4m)x2y+m(9n-5)xy=4mx2y+9mnxy-5mxy.
Theorem2LetVPHX[m,n] be V-Pheylenic Nanotube. Then
CM1(VPHX[m,n])=2m(1+9n).
ProofBy using the definition of reverse second Zagreb index and reverse edge partition of V-Phenylenic Nanotube given in Table 2, we have

=3|CE1(VPHX[m,n])|+2|CE2(VPHX[m,n])|
=3(4m)+2(m(9n-5))=2m(1+9n).
Theorem3LetVPHX[m,n] be V-Pheylenic Nanotube. Then
CM2(VPHX[m,n])=3m(1+3n).
ProofBy using the definition of reverse modified second Zagreb index and reverse edge partition of V-Phenylenic Nanotube given in Table 2, we have
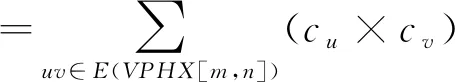
=2|CE1(VPHX[m,n])|+1|CE2(VPHX[m,n])|
=2(4m)+1(m(9n-5))=3m(1+3n).
Theorem4LetVPHX[m,n] be V-Pheylenic Nanotube. Then
CmM2(VPHX[m,n])=3m(3n-1).
ProofBy using the definition of reverse modified second Zagreb index and reverse edge partition of V-Phenylenic Nanotube given in Table 2, we have

Theorem5LetVPHX[m,n] be V-Pheylenic Nanotube. Then
ProofBy using the definition of reverse harmonic index and reverse edge partition of V-Phenylenic Nanotube given in Table 2, we have
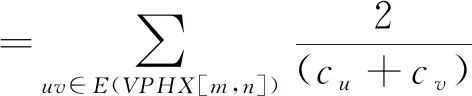
Theorem6LetVPHX[m,n] be V-Pheylenic Nanotube. Then
ProofBy using the definition of reverse inverse sum index and reverse edge partition of V-Phenylenic Nanotube given in Table 2, we have

3 Concluding Remarks
In this paper we have defined some new indices and computed for V-Phenylenic Nanotube. Our results will be a good addition in the field of chemical graph theory. To define reverse version of other degree based topological indices is an interesting problem.
