碳纳米锥的基于乘法度的拓扑指数

穆罕默德·阿比德·萨利姆，穆罕默德·阿西夫，阿拜德·雷曼·维克

(1．巴哈丁扎卡利亚大学 数学系，木尔坦 60800；2．民哈吉大学 数学系，拉合尔 54000；3．拉合尔管理技术大学 数学系，拉合尔 54000)

Carbon nanocones have been observed since 1968 or even earlier[1], on the surface of naturally occurring graphite. Their bases are attached to the graphite and their height varies between 1 and 40 micrometers. Their walls are often curved and are less regular than those of the laboratory made nanocones. Carbon nanostructures have attracted considerable attention due to their potential use in many applications including energy storage, gas sensors, biosensors, nanoelectronic devices and chemical probes[2]. Carbon allotropes such as carbon nanocones and carbon nanotubes have been proposed as possible molecular gas storage devices[3]. More recently, carbon nanocones have gained increased scientific interest due to their unique properties and promising uses in many novel applications such as energy and hydrogen-storage[4]. Figure 1 and figure 2 are carbon nenocones.

The molecular graph of nanocones have conical structures with a cycle of lengthkat its core andnlayers of hexagons placed at the conical surface around its center as shown in following figure 3.

In the present report, we gave closed form of multiplicative versions of some important degree-based TIs.

1 Definitions of TIs

In this section, we present definitions of multiplicative versions of TIs.

Definition1(First Generalized Multiplication Zagreb Index)

For a connected simple graphG, the first generalized multiplication Zagreb index[5]is defined as：

Definition2(Second Generalized Multiplication Zagreb Index)

For a connected simple graphG, the second generalized multiplication Zagreb index[5]is defined as：

Definition3(First Multiplication Zagreb Index )

For a connected simple graphG, the first multiplication Zagreb index[6]is defined as：

Definition4(Second Multiplication Zagreb Index )

For a connected simple graphG, the second multiplication Zagreb index[6]is defined as:

Definition5(First Hyper Multiplication Zagreb Index )

For a connected simple graphG, the first hyper multiplication Zagreb index[7]is defined as：

Definition6(Second Hyper Multiplication Zagreb Index )

For a connected simple graphG, the second hyper multiplication Zagreb index[7]is defined as：

Definition7(Multiplicative Sum Connectivity Index)

For a connected simple graphG, the multiplicative sum connectivity index[8]is defined as：

Definition8(Multiplicative Product Connectivity Indices )

For a connected simple graphG, the multiplicative product connectivity index[8]is defined as:

Definition9(Multiplicative Atomic Bond Connectivity Index)

For a connected simple graphG, the multiplicative atomic bond connectivity index[8]is defined as：

Definition10(Multiplicative Geometric Arithmetic Index)

For a connected simple graphG, the multiplicative geometric arithmetic index[8]is defined as:

2 Computational Results

In this section, we present our results. From figure 3, it can be observed that the edge set molecular graph of Carbon nanocone can be divided into three classes based on the degree of end vertices. The edge partition of molecular graph of Carbon Nanocone is presented in Table 1.

Table 1 Degree based edge partition of G

Theorem1LetGbe the molecular graph of Carbon nanocone. Then we have

ProofBy the Definition of the generalized first multiplication Zagreb index and using edge partition of molecular graph of Carbon Nanocone, we have following computation:

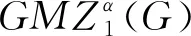
=(4α)|ij∈E1(G)|×(5α)|ij∈E2(G)|×(6α)|ij∈E3(G)|

Theorem2LetGbe the molecular graph of Carbon nanocone. Then we have

ProofBy the Definition of the generalized first multiplication Zagreb index and using edge partition of molecular graph of Carbon Nanocone, we have following computation:

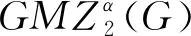
=(4α)|ij∈E1(G)|×(6α)|ij∈E2(G)|×(9α)|ij∈E3(G)|

Corollary1LetGbe the molecular graph of Carbon nanocone. Then we have

ProofTakingα=1 in Theorem 1, we get this result immediate.

Corollary2LetGbe the molecular graph of Carbon nanocone. Then we have

ProofTakingα=1 in Theorem 2, we get this result immediate.

Corollary3LetGbe the molecular graph of Carbon nanocone. Then we have

ProofTakingα=2 in Theorem 1, we get this result immediate.

Corollary4LetGbe the molecular graph of Carbon nanocone. Then we have

ProofTakingα=2 in Theorem 2, we get this result immediate.

Corollary5LetGbe the molecular graph of Carbon nanocone. Then we have

ProofTaking α=-1/2 in Theorem 1, we get this result immediate.

Corollary6LetGbe the molecular graph of Carbon nanocone. Then we have

ProofTaking α=-1/2 in Theorem 2, we get this result immediate.

Theorem3LetGbe the molecular graph of Carbon nanocone. Then we have

ProofBy the Definition of the multiplication Atomic bound Connectivity index and using edge partition of molecular graph of Carbon Nanocone, we have following computation:

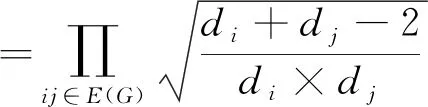
Theorem4ForG, We have

ProofBy the Definition of the multiplication Geometric arithmetic index and using edge partition of molecular graph of Carbon Nanocone, we have following computation:

3 Conclusion

In this paper, we computed multiplicative versions of several degree-based TIs for molecular graph of Carbon nanocones. Our result can help in understanding topology of concerned nanocone and in guessing its properties. In future, we are interested in computed distance based polynomials and indices for it.