匹配数为2的单圈图最大匹配根排序

郭　强



匹配数为2的单圈图最大匹配根排序

郭强

（南通大学 理学院，江苏 南通 226019）

设是一个具有个点的简单连通图，图的匹配多项式定义为。文章通过对单圈图的匹配多项式进行计算，对匹配数为2最大匹配根进行了大小排序。

单圈图；匹配多项式；匹配数；最大匹配根

1　引　言

自从1736年数学家Euler发表了第一篇有关图论的文章之后便产生了密切联系实际的图论学科。多项式是处理图的常用的代数工具，比较常见的有各种矩阵的特征多项式，为组合计数而产生的伴随多项式、匹配多项式、色多项式等等。匹配多项式是这个图上的匹配数的一种生成函数。设是一个阶图，的一个匹配是指的一个生成子图，它的每个分支或是孤立点或是孤立边。设为个顶点的简单图，其顶点集为，边集为。图的匹配多项式为[4]，其中表示匹配数为的数目。设表示点的邻点的集合，表示点的度，显然点的度就等于。表示图的最大匹配根。匹配多项式有很多很好的性质，它的根都是实数并且关于原点对称；它的某种积分可以计算满足某些条件的排列的个数[5-6]；它和图的特征多项式之间有深刻的联系，如在树上匹配多项式等于特征多项式；对于一般的图，匹配多项式是这个图上定义的一种路树的特征多项式的一个因子。匹配多项式和匹配的研究不仅有数学上的价值，更有化学和物理上的应用背景。

2　主要引理

引理1[1]：设是图的生成子图，为图的最大匹配根，如果，则有。如果是图的真子图并且，则有。

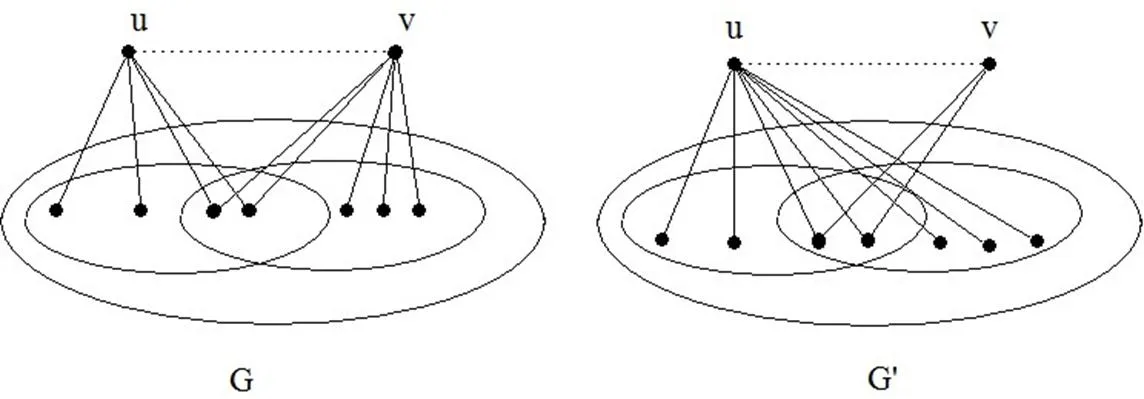
图1

引理2[2]：如果图是有图经过Kelmans变换得到的，那么。

引理3[3]：假设图和是如图2所示的单圈图，如果，那么，当且仅当时等号成立。

图2

引理4[3]：在所有个点的单圈图里()，从第一大到第四大的最大匹配根，，，。

3　结　论

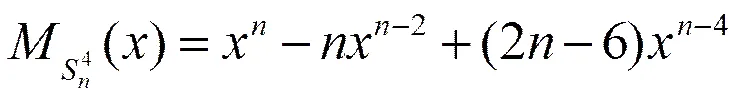
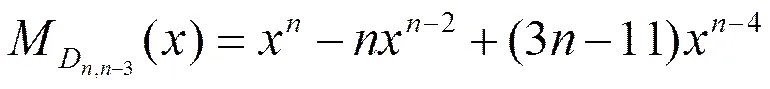
可以得到

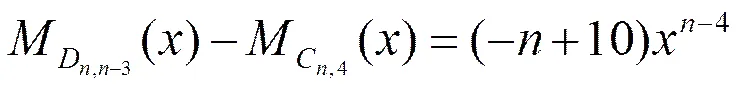
结合引理3和引理4得证。

[1]D.Cvetkovi´c,M.Doob,I.Gutman,A.Torgaˇsev,Recent Results in the Theory of Graph Spectra[J],North–Holland,Amsterdam,1988.

[2]A.K.Kelmans,On graphs with randomly deleted edges[J].Acta.Math.Acad.Sci.Hung.37(1981):77-88.

[3]Weijun.Liu,Further results on the largest matching root of unicyclic graphs[J].submitted.

[4]C.D.Godsil and I.Gutman.On the Theory of the Matching Polynomials,[J].Graph Theory,5(1981):79-87.

[5]C.D.Godsil. Hermite polynomiala and a duality relation for matching polynomials[J].Combinnatorica,1(3)(1981).257-262.

[6]C.D.Godsil.Algebraic Combinatorics[J].New York.London:Chapman and Hall,1993.

（责任编校：何俊华）

2016－03－02

郭强（1990－）湖南沅江人，南通大学硕士研究生，研究方向为代数组合。

0151

A

1673-2219（2016）05-0006-03