一类单圈图的最大独立集的交
2021-12-20谢佳漫
谢佳漫,王 艳
(闽南师范大学 数学与统计学院,福建 漳州 363000)
独立集理论是图论重要的研究领域之一,其中最大独立集问题是图论的热点研究问题.1990年,张存铨提出一类临界独立集问题[1].记独立集的个数减去其邻集的个数的值为独立集的差,临界独立集是指某个独立集满足其差在所有独立集的差中取得最大值.近几年来,研究表明最大独立集问题与临界独立集问题之间存在着密切的联系.为此,针对这两类独立集,我们研究一类单圈图的相关性质.
1 预备知识
本文所考虑的图均为有限简单图G=(V(G),E(G)),其中集合V(G)为G的顶点集,集合E(G)为G的边集.对于v∈V(G),称N(v)={w∈V(G):vw∈E(G)}为v∈V(G)的邻集;对于X⊆V(G),称N(X)={v:v∈V(G)且N(v)∩X≠∅}为X的邻集;称N[X]=X∪N(X)为X的闭邻域;称d(X)=|X|-|N(X)|为X的差,特别地,d(∅)=0;称d(G)=max{d(X):X⊆V(G)}为G的临界差;若X满足d(X)=d(G),则称X为临界集.令ker(G)为G的所有临界集的交.Levit等人在2012年证明了G的所有临界独立集的交等于ker(G)[2].
若X中任意两个顶点都不相邻,则称X为独立集;记独立集族ind(G)={X:X为G的独立集};设X∈ind(G),∀X′∈ind(G),|X′|≤|X|,则称X为最大独立集,记最大独立集的顶点数为α(G);令core(G)为G的所有最大独立集的交.
在图G中ker(G)⊆core(G)[2];当图G为二部图时,则ker(G)=core(G)[3].
对于M⊆E(G),若M中任意两条边都不相邻,则称M为G的匹配.记m∈M为匹配边;若匹配M中某条边与v关联,则称M饱和v;记|M(G)|为G的匹配边数;若|M(G)|在G中取得最大值,则称为最大匹配M,记最大匹配数为μ(G);若匹配M能匹配G的所有顶点,则称M为完美匹配;称MΔM′=M∪M′-M∩M′为匹配M和M′的对称差.

对于X⊆V(G),G[X]为由X⊂V(G)所导出G的子图.对于M⊆E(G),G[M]为由M⊂E(G)所导出G的子图.设G的点边交替序列W=v0e1v1e2…vl-1elvl,其中1≤i≤l,ei=(vi-1,vi),称W为G的一条路径;称整数l为W的长;若l>0,vi≠vj(0≤i 在单圈图G中,|V(G)|-1≤α(G)+μ(G)≤|V(G)|[6];在非König-Egerváry单圈图中,ker(G)=core(G)[7],但在König-Egerváry单圈图中,ker(G)=core(G)不一定成立.例如,在图1中ker(G1)={x,y}但core(G1)={x,y,z}而ker(G2)=core(G2)={a,b,c}. 图1 König-Egerváry单圈图 若单圈图G有完美匹配,则α(G)=μ(G)=|V(G)|/2,故α(G)+μ(G)=|V(G)|,所以图G为König-Egerváry图. 如果能刻画满足ker(G)=core(G)的非二部的单圈König-Egerváry图,我们将更进一步了解单圈图的性质.为此,我们探讨非二部的单圈König-Egerváry图的特殊情况,即具有完美匹配的非二部的单圈图,研究其ker(G)和core(G)的性质. 本节先介绍具有完美匹配的非二部的单圈图G的基本性质及其ker(G),再分两步论证其core(G). 性质1 若图G为非二部的单圈图且包含完美匹配,则下列结论成立: (1)圈为奇圈; (2)完美匹配是唯一的. 证明: (1)显然成立,若圈为偶圈,则图G为二部图.(2)如果不唯一,则图G至少存在两个完美匹配,分别为M、M′,则MΔM′必为偶圈,而与单圈非二部图矛盾.故命题成立. □ 性质2 若图G为非二部的单圈图且包含完美匹配,则ker(G)=∅. 证明: 由于图G有完美匹配,故对于任意X⊆V(G),|N(X)|≥|X|恒成立,即d(X)≤0.故临界差d(G)=0.而空集的差为0,故空集为临界集,因此空集与任一临界集的交为空集,故ker(G)=∅. 在单圈图G上,对G的完美匹配M进行划分,分别为M1=M∩E(C),M2=M∩E(N[C])-M1,M3=M-M1-M2. 首先考虑M3=∅的情形.由性质1可知,图G有唯一的完美匹配和奇圈,则匹配在圈C上的边数是唯一确定的且α(G)=|V(G)|/2.接下来对匹配在圈C上的边数进行分类讨论core(G).为了方便讨论,先将图G划分为A,B两部分:设B为最大独立集,即|B|=|V(G)|/2,A中只有两个点相邻,使得从A到B有完美匹配.显然A中相邻的两个点在圈C上.另外,圈C上的点在A的点数比在B的点数多1. 定理3 若图G为1个奇圈加1条悬挂边,记悬挂点为b,则core(G)={b}. 证明: 显然|M2|=1且b被M2饱和.记被M2饱和的另一个顶点为a.此时,点a、b分别属于A和B.令a为A中相邻的两个点之一,如图2所示. 图2 图G为1个奇圈加1条悬挂边 此时{b}∩(A{a})=∅,又因为A{a}中的点互不相邻,且|A{a}|=|B|-1,故{b}∪(A{a})为G的最大独立集,记为B′.而当G-b为圈C,其最大独立集的顶点数为|B|-1,故G-b中不存在G的最大独立集.又因为B=(M1∩B)∪{b},因此core(G)=B∩B′={b},故结论成立. □ 定理4 若图G为1个奇圈加若干奇数(大于1)条悬挂边,则core(G)=∅. 证明: 记在圈C中被M2所饱和的点的个数记为t,其中3≤t≤|V(C)|且t为奇数.设M2={m1,m2,…,mi,…,mt},其中1≤i≤t.令mi=aibi,其中ai∈V(C),bi∉V(C),如图3所示. 图3 图G为1个奇圈加若干奇数(大于1)条悬挂边 □ 我们接下来考虑M3≠∅的情形.在图G中,设∂(X)={uv∈E(G):u∈X,v∈VX}为X的边割. 在非二部的单圈图G且包含完美匹配中,记顶点集合X=V(C)∪{v:被M2饱和的顶点},顶点集合Y=V(G)X.此时G[Y]为森林,每一棵树Tj有完美匹配,其中1≤j≤c(G[Y]),这里c(G[Y])表示G[Y]的连通分支数;边割∂(X)=∂(Y)=c(G[Y])且对于e=xjyj∈∂(X),其中xj∈V(X),yj∈V(Y),e不是G的完美匹配边.设树Tj的根为yj. 因为树Tj是二部图且有完美匹配,因此存在两个不同的最大独立集Aj和Bj,使得树的完美匹配边的端点分别来自Aj、Bj.故Aj∩Bj=∅,Aj∪Bj=V(Tj),且|Aj|=|Bj|=|V(Tj)|/2. 结合情形M3=∅的图,对G[X]划分为A,B两部分:设B为最大独立集,|B|=|V(G[X])|/2,A中只有两个点相邻,使得从A到B有完美匹配.显然A中相邻的两个点在圈C上.另外,圈C上的点在A的点数比在B的点数多1.若xj∈A,则令yj所在的集合为Bj;否则令yj所在的集合为Aj,此时{xj}∪Bj为独立集.接下来对匹配在圈C上的边数进行分类讨论core(G). 证明: 在G[X]中取两个最大独立集为B和B′,且B∩B′={b},其中b为圈C外被M2饱和的顶点且b∈B,其取法和记法与定理3的证明中相同.按下述取法取两个G的最大独立集分别为S、S′. 此时, 而在G-b中,其最大独立集的个数为 而G的最大独立集的个数为|V(G)|/2,故在G-b中,不存在G的最大独立集.故b∈core(G). 另一方面,由于b∈core(G),则N(N(b)∩Y)⊆core(G),显然 又因为Tj为一棵树中,则包含N(N(b)∩Y){b}的最大独立集Bj是唯一的,故 □ 定理6 若单圈图G(设G包含的圈为C)为非二部图且包含完美匹配M,满足|E(C)∩M|<(|E(C)|-1)/2,则core(G)=∅. 证明: 此时, □ 利用反证法,由定理5和定理6可知, 推论8 若单圈图G(设G包含的圈为C)为非二部图且包含完美匹配M,则core(G)=∅当且仅当|E(C)∩M|<(|E(C)|-1)/2. 由性质2可得, 推论9 若单圈图G(设G包含的圈为C)为非二部图且包含完美匹配M,则ker(G)=core(G)=∅当且仅当|E(C)∩M|<(|E(C)|-1)/2. 在本文中,通过研究包含完美匹配的单圈图的最大独立集的交、临界集的交以及它们之间的关系,得到了两类独立集的交相等的等价条件.在后续的研究中,我们可以利用这个结论,进一步研究相关单圈图的刻画,并探讨单圈图的最大独立集的交与临界集的交之间的关系.
2 主要结果










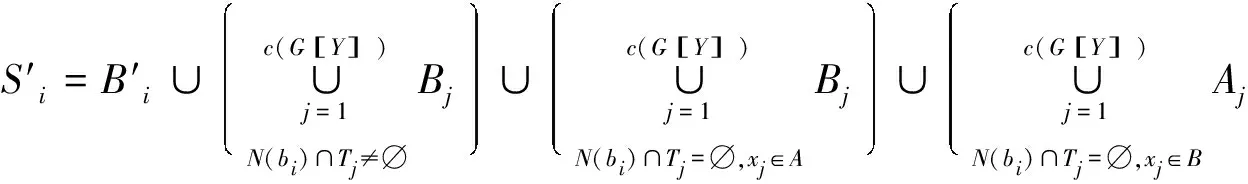


3 结束语
