具有最多与最少连通子图的单圈图

洪雅丽

(晋江市南侨中学，福建 泉州 362200)

设T 是一棵树，它的一个连通的导出子图称为一个子树。子树的计数问题被广泛研究，Székely与Wang［1］考虑了二元树的子树的计数问题，得到了具有最多子树的二元树，Yan 与Yeh［2］给出了两个线性算法计算树的子树的数目，Li 与Wang［3］进一步分析研究了树的子树的计数问题。有关计算树的子树数目见相关文献。［4－10］一个自然的问题是:考虑单圈图的连通子图的计数问题。袁新梅［11］给出了一个线性算法计算单圈图的连通子图的数目。在此基础上，下文主要考虑连通单圈图的连通子图数目的极值问题。

1 基本术语与基本结果

为了描述方便，采用文［2，11］中的符号与基本术语。

除特别说明外，假设G = {V(G)，E(G);f，g}为一带权单圈图，其中V(G)= {v1，v2，…，vn}为顶点集合，E(G)= {e1，e2…，en}为边集合，顶点的带权函数为f:V(G)→R，边的带权函数为g:E(G)→R(其中R 表示非负实数集)。如果一带权单圈图G = {V(G)，E(G);f，g}满足f = g =1 ，称G 为一简单单圈图。对于一个给定的带权单圈图G的连通子图G1，定义G1的权是G1里所有顶点与边的权的乘积，用ω(G1)来表示。带权单圈图G= (V(G)，E(G);f，g)的所有连通子图的权之和用F(G;f，g)表示。定义带权单圈图G = (V(G)，E(G);f，g)包含一个固定顶点vi的连通子图的权和为包含顶点vi的G 的连通子图的权的和，用F(G;f，g;vi)表示。假设G 是一个n 个顶点的简单单圈图，用χ(G)= F(G;1，1)来表示G 的连通子图的数目，G 的包含顶点vi的连通子图的数目表示为χ(G;vi)= F(G;1，1;vi)。

令G 是n(n ＞1)个顶点并且含一片叶子u 的单圈图。假设G 的悬挂边为e = (u，v)。定义顶点个数为n－1 的一个带权单圈图G' = (V(G')，E(G');f＇，g＇)，其中V(G')= V(G) {u}，E(G')= E(G) {e}，

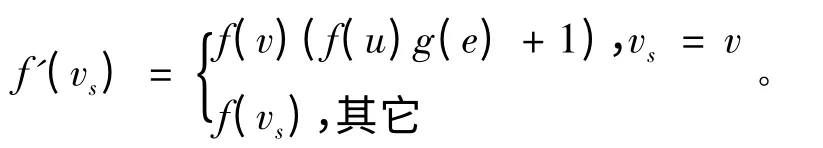
对于任意的vs∈V(G')，对于任意的e ∈E(G')，有g＇(e)= g(e)。图1 与图2 说明了由G构造G' 的过程。

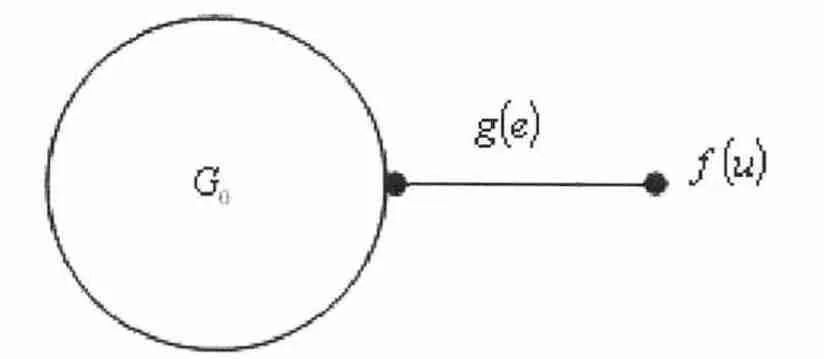
图1 权单圈图G = (V(G)，E(G);f，g)及其一悬挂边e = (u，v)

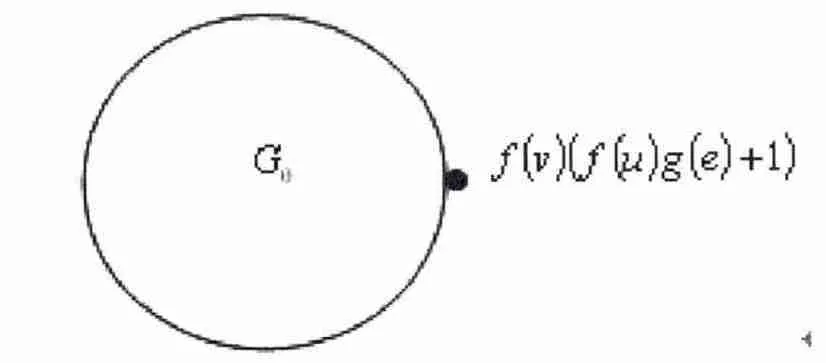
图2 对应的权单圈图G' = (V(G')，E(G');f＇，g＇)

定理1.1［11］根据上面的记法，有F(G;f，g)= F(G';f'，g')+ f(u)。

利用此结果，袁［11］给出了计算连通的单圈图的连通子图的计数方法。

定理1.2［11］令G = (V(G)，E(G))是有n(n＞1)个顶点的简单单圈图，其中圈上有l 个顶点，记为v1，v2，…，vl，Ti(i = 1，2，…l)为附在圈上且包含顶点vi树，则:

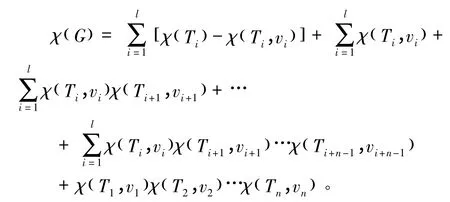
2 主要结果

在下文中，除特别说明外，单圈图均为简单图。

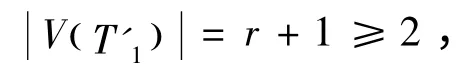
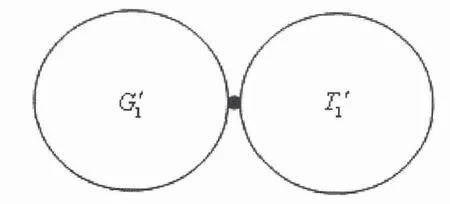
图3 由单圈图G'1 与树T'1 构造得到的单圈图G1

图4 通过G'1 的顶点u

附上r 个悬挂边而得到的图G2

定理2.1 令G1和G2是如上定义的单圈图，当r ≥1 即有:χ ( G2)= F ( G2;1，1 )，等号成立当且仅当T'1= K1，r且dT'1( )v = r。

证明:令fi:V ( G'1)→R ( i = 1，2 )为两个如下

定义的函数:

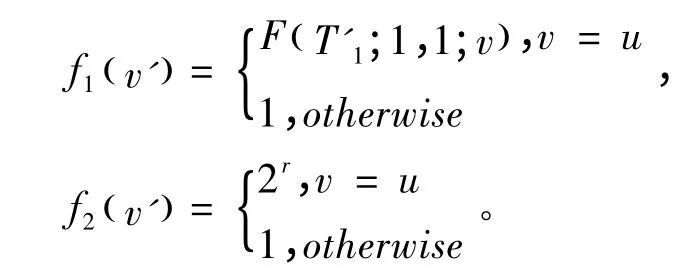
其中F (T'1;1，1;V )是T'1中包含顶点v 的子树数。

由定理2.1 得:

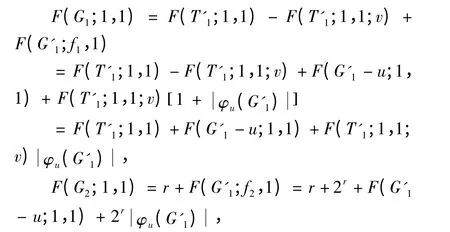
即:

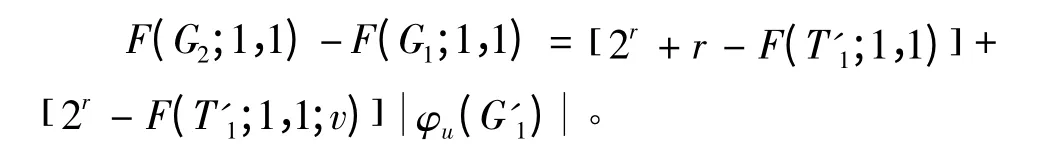
注意到:T'1是含有r +1 个顶点的树，有2r+r－F(T'1;1，1)≥0 ，等号成立当且仅当T'1= K1，r。因为T'1至少有r 个含一个顶点vi(vi≠v)的子树，则F(T'1;1，1)≥F(T'1;1，1;v)+ r。

注 意 到，F(K1，r;1，1) = 2r+ r，即:0 ≤F(K1，r;1，1)－ F(T'1;1，1)≤2r－F(T'1;1，1;v)。

所以2r－F(T'1;1，1;v)≥0(等号成立当且仅当T'1= K1，r且dT'1(v)= r)。

因此有χ(G1)= F(G1;1，1)≤χ(G2)= F(G2;1，1)。

等号成立当且仅当T'1= K1，r且dT'1(v)= r。即定理得证。

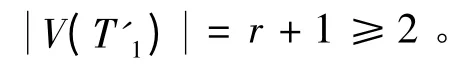
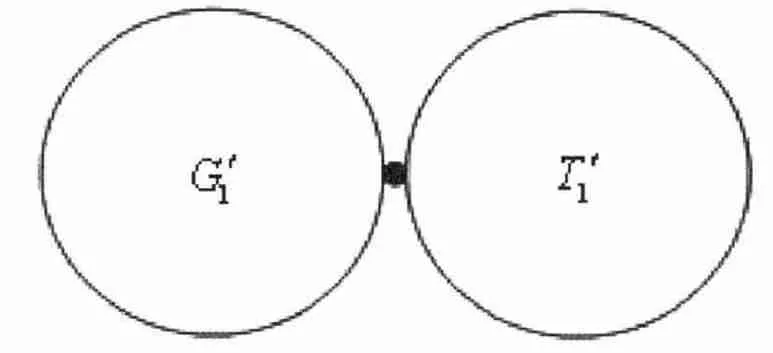
图5 由单圈图G'1 与树T'1构造得到的单圈图G1

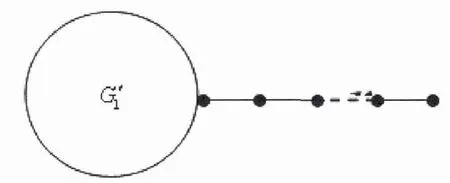
图6 通过G'1 的顶点u 附上一条长为r 的路而得到的图G3

定理2.2 令G1和G3是如上定义的单圈图，且r ≥1 。则χ(G1)= F(G1;1，1)≥χ(G3) =F(G3;1，1)。

当且仅当T'1= Pr+1且dT'1(v)= 1 时等号成立。

令Gd是没有叶子圈长为d 的单圈图，G 是由Gd将ki个悬挂边附于顶点vi而生成的，i = 1，2，... ，d(见图7)。单圈图G*是在没有叶子的单圈图Gd的顶点vh上附于个悬挂边而生成的(如图8)。

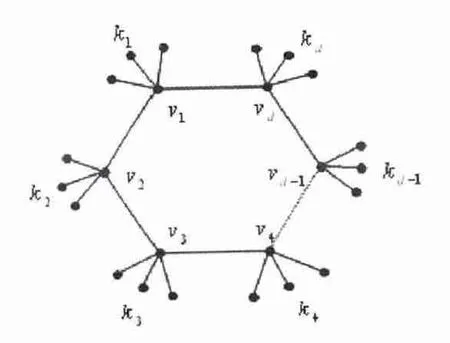
图7 由Gd 将ki(i = 1，2，... ，d)个悬挂边附于vi 而生成的单圈图G = Gd(k1，k2，…，kd)

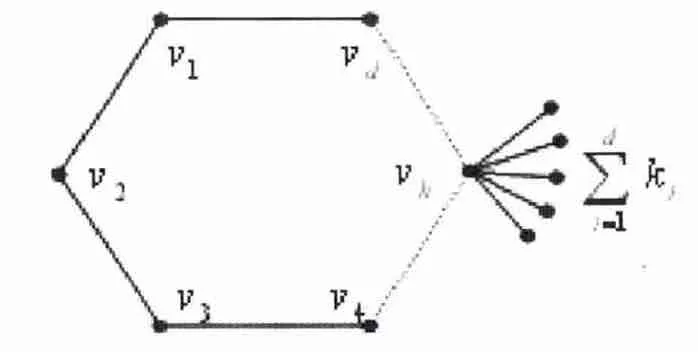
图8 在没有叶子的单圈图Gd 的顶点vh 上附于个悬挂边而生成的单圈图G*

定理2.3 令G 和G*为如上定义的两个单圈图，k1，k2，…，kd至少有两个不为零。则F(G;1，1)＜F(G*;1，1)。

证明:根据定理2.2，有

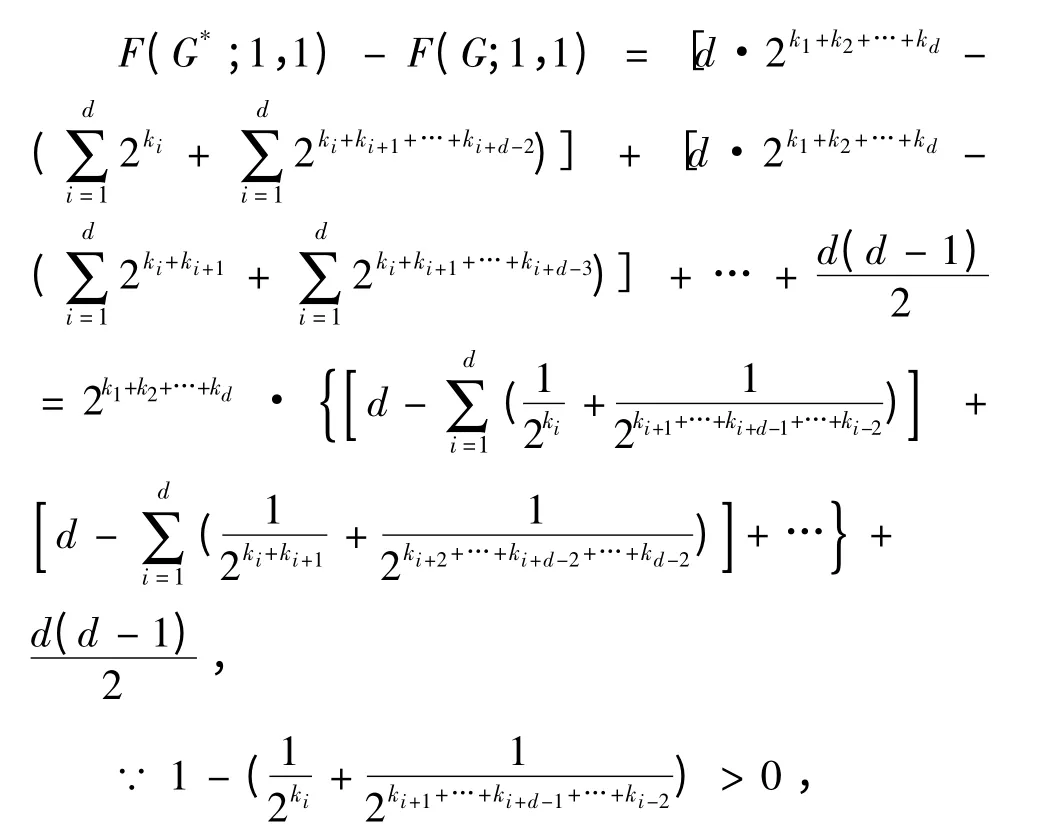
以此类推，可得

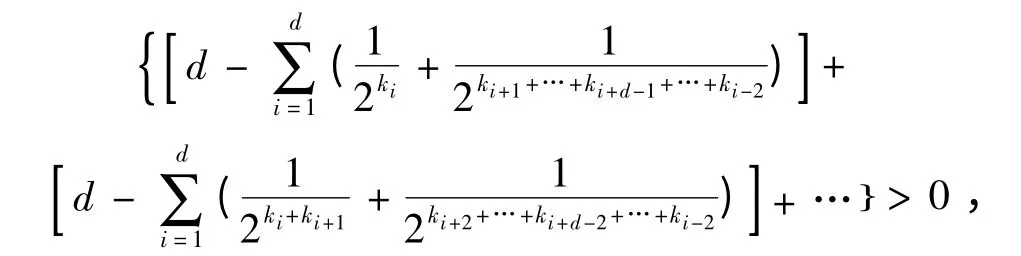
又因为2k1+k2+…+kd＞0 ，d ≥3 ，

所以F(G*;1，1)－ F(G;1，1)＞0 。

因此有F(G;1，1)＜F(G*;1，1)。

从而定理成立。

令G0是没有叶子的单圈图，其圈上有d 个顶点，分别为v1，v2，…，vd。现将每个顶点vi(1 ≤i ≤d)上附于一条有ki个顶点的路，生成G＆(如图9)。vh是G0的一个顶点，在G0的顶点vh上附于一条有个顶点的路，生成G#(如图10)。

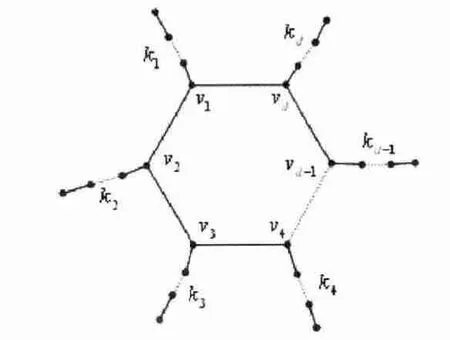
图9 单圈图G＆

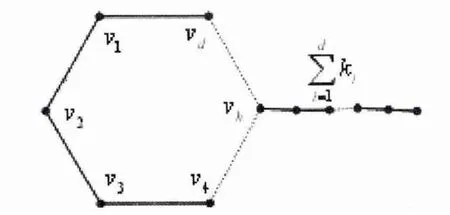
图10 单圈图G#

定理2.4 令G＆和G#为如上定义的单圈图，且至少有两个ki不为零，则χ(G＆)= F(G＆;1，1)＜χ(G#)= F(G#;1，1)。

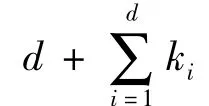
成立当且仅当G = G*。

［1］Székely LA，Wang H.On subtrees of trees［J］.Adv.Appl.Math，2005，34(1):138－155.

［2］Yan WG，Yeh YN.Enumeration of subtrees of trees［J］.Theoretical Computer Science，2006，369:256－268.

［3］Li SC，Wang SJ.Further Analysis on the Total Number of Subtrees of Trees［J］.The Electronic Journal of Combinatorics，2012，(19):48.

［4］Székely LA，Wang H.Binary trees with the largest number of subtrees with at least one leaf［J］.Congr.Numer.，2005，177:147－169.

［5］Wang H.Some results on trees［M］.Ph.D.Thesis，Department of Mathematics，University of South Carolina，2005.

［6］ Wagon S.A bound on the chronmatic number of graphs without certain induced subgraphs［J］.J.Combin.Theory.Ser.B，1980，29:245－246.

［7］Walter JR.Representations of chordal graphs as subtrees of a tree［J］.J.Graph Theory，1978，(2):265－267.

［8］Wang DL，Kleitman DJ.On the existence of n－connected graphs with prescribed degrees(n ≥2)［J］.Networks，1973，(3):225－239.

［9］Bondy J.A，Murty U.S.R.Graph Theory with Applications［M］.Macmillan Press LTD，1976.

［10］袁新梅. 单圈图的连通子图的数目［J］. 南开大学学报(自然科学版)，2011，44(3):23－27.