一种提高飞行器结构天地力学环境地面试验有效性的方法及其应用

阎桂荣，董龙雷，宋利强

（西安交通大学 机械结构强度与振动国家重点实验室，西安 710049）

一种提高飞行器结构天地力学环境地面试验有效性的方法及其应用

阎桂荣，董龙雷，宋利强

（西安交通大学 机械结构强度与振动国家重点实验室，西安 710049）

目的 研究提高飞行器结构地面试验有效性的途径。方法 计算同一被试件结构在飞行状态和地面试验状态下的有限元模型，测量地面试验状态下的模态以验证有限元模型的正确性；计算各特征点（也可以是遥测点）在天地状态下的响应，用机器学习法获取各特征点的映射关系模型；基于该模型由飞行点响应（或遥测数据）确定出地面试验件对应点的响应，并用载荷反求法得到它们的等效载荷；最终确定施加在试验系统上的载荷。结果 以细长体结构为例，所得到由其组成试验系统的有限元模型与实测模型之间的固有频率最大相对误差为 6.76%，利用映射关系模型预测出对应点在飞行状态下的振动响应。确定了飞行状态下结构响应的特征点，由地面试验系统所对应的响应点反推出应施加的载荷为60 N。结论 利用天地数值计算-地面试验验证联合法，无需在地面试验状态下刻意模拟飞行状态的边界条件，确定出所需要施加的载荷，从而提高了飞行器地面试验的有效性。

振动试验；映射关系模型；有限元分析；试验有效性

地面振动试验是飞行器研制全过程中的重要环节，地面振动试验的有效性不仅直接关系到飞行器的工作可靠性及性能，而且对飞行器的精细化设计具有更重要的意义，但如何提高地面试验的有效性是一个值得深思的问题。提高地面试验的有效性，需要解决两个关键问题：要制定正确的地面试验规范或条件；要能够准确地实现试验规范，即给出试验方法。对于地面试验规范的制定，最常用的方法有两类：总体设计部门多用类比法、归纳法、包络法、外推法等，随着数值计算的日趋完善，有限元法也受到青睐；另一类的依据就是国内外制定的环境振动试验标准，试验标准只是规定了试验条件，并未告知这些试验条件如何得到的。准确地实现试验规范就是按照所制定的试验规范给出试验条件并实现它。当一个结构设计完成后，其固有特性就确定了，其结构的振动响应还与边界条件、载荷有关。载荷是外激励，它通过结构的固有特性影响着振动响应。边界条件一旦确定，就影响着系统的固有特性。边界条件参数的影响却难以模拟，特别在试验台上安装的零部件、分系统，很难模拟出它们在飞行器整体结构上的联接方式。为了考核零部件、分系统在地面试验装置上的响应，通常以结构的局部响应等效为依据。由于试验系统本身的动力学特性、及试件在试验系统中的安装条件所限，结构局部响应等效多是依靠试验系统控制器的负反馈实现。虽然被控点可以满足规范要求，但未控点可能会出现过试验或欠试验状况，特别是对大型结构，甚至会出现试验难以进行而不得不修改试验条件的局面[1—3]。

细长体结构是火箭、导弹等常用的结构，文中将以其为对象介绍一种飞行器结构天地数值计算-地面试验验证联合法，以提高地面试验的有效性。

1　理论基础

1.1 映射关系模型

映射关系模型是应用天地数值计算-地面试验验证联合法的基础。映射关系就是将输入空间的变量映射到高维的特征空间，在高维空间中寻求它们的关系，利用映射关系获取的模型称为映射关系模型[4]。

文献[4]中还引入了一个时域决策函数 ψi(t)，而 ψ(t)为时域决策函数 ψi(t)的集合，ψ(t)描述了相同载荷下系统1和系统2各对应点时域响应之间的关系。

根据文献[4]的证明和对基于时域的第一映射关系模型和基于频域的第二映射关系模型定义，发展了天地数值计算-地面试验验证联合法（简称联合法）。所谓“天”是指飞行器被试部件（或整体）结构的飞行状态，所谓“地”是指飞行器被试部件（或整体）结构在试验系统中的状态，需要指出的是无须对结构在试验系统中的边界条件提出模拟飞行状态的要求。

1.2 实施步骤

以映射关系为理论基础，以机器学习为基本算法，实现天地数值计算-地面试验验证联合法的主要步骤如下。

1) 建立被试部件结构在飞行状态下（简称系统1）的有限元模型，建模时应考虑总体结构前后连接件对该限元模型的影响。

2) 建立被试部件结构在地面试验状态下（简称系统2）的有限元模型，此时也应考虑试验系统通过各联接件对被试件有限元模型的影响。

3) 分别对系统1、系统2中被试部件结构各点的响应进行聚类，以确定并关注其响应特征点的位置。

4) 建立被试部件结构的天地响应的映射关系模型。具体做法是给系统1和系统2的有限元模型施加相同的载荷，为了能反映被试件的特性，载荷的类型应为平谱，且参加机器学习的训练样本载荷的涵盖范围足够宽。

5) 试验验证。其目的为验证结构在系统 2中所建有限元模型的正确性；从系统2实测结构的振动响应预测出结构在系统1的响应。

6) 确定施加在系统2上的载荷。具体做法是：由步骤3）确定系统1聚类的特征点和步骤4）取得的与特征点对应的系统 2上结构的响应样本和模型，反求出一组被试件上的载荷（u1，u2，…，un）[5—8]；通过映射关系模型和系统1测得的遥测信号，确定相应的载荷ui；利用该点的载荷ui与实际加载点之间的传递函数求出实际加载点的载荷。

7) 假设取m个特征点，可得到一组数据（um1，um2，…，umm），选取该组的最大值或程控法作为实际施加载荷，完成地面考核试验。

2　试验系统研究

以一个细长体结构为实例，介绍天地数值计算-地面试验验证联合法的具体应用。

2.1 试验系统设计

围绕实现天地数值计算-地面试验验证联合法的目标，设计了一个细长体结构试验件，该试验件由圆柱壳、截锥壳、二次曲面壳、后盖板组成，后盖板和圆柱壳、圆柱壳和截锥壳、截锥壳和二次曲面壳的连接方式都是内外螺纹紧配合。细长体结构试验件借助于两个支座安装于底板上，形成地面试验系统，如图1所示。

图1 试验系统Fig.1 Test system

试验件尾部安装了一个振动台作为外激励。系统还包括传感器-测试分析系统，用于完成试验建模、结构响应测试。

2.2 系统建模

利用子结构法测取整体结构的模态，完成系统建模。测点布置、测点数量的选择基于下述原则：能够明确显示在试验频段内所有模态的基本特征及相互间的区别，保证关心的结构点都在所选的测点之中；为提高信噪比，测点不应选在各阶振型节点附近。根据以上原则，在试验对象上选择了138个测试点，为保证不遗漏重要模态，在圆柱壳上选择7个激励点，在每个支架上选择一个激励点。拾取各激励点锤击激励下+x，+y，+z方向的响应信号，并计算出所有的频率响应函数FRF。用LSCF法进行参数识别，模态识别稳态图如2所示，分析带宽取为10～512 Hz。

图2 平台总频响的稳态图Fig.2 The steady-state frequency response diagram of the system

结合稳态图、各敲击点数据的对比和MAC表及振型分析，通过对参数识别的结果进行比较可知，不同方向、不同点激励以及不同方向频率响应分析结果基本一致，综合分析后所得平台模态描述见表1，模态振型如图3所示。为保证试验模型的有效性和正确性，用互易性检验、相干性检验、MAC值检验等方法对试验结果进行了检验。

表1 平台的固有频率Table 1 Natural frequency of the system

图3 平台整体前六阶振型Fig.3 The preceding six mode shapes of the system

3　数值仿真

3.1 无边界条件约束

为模拟飞行状态，建立了被试件的有限元模型如图4所示，模态描述见表2，模态振型如图5所示。

图4 试验件有限元模型Fig.4 The finite element model of the specimen

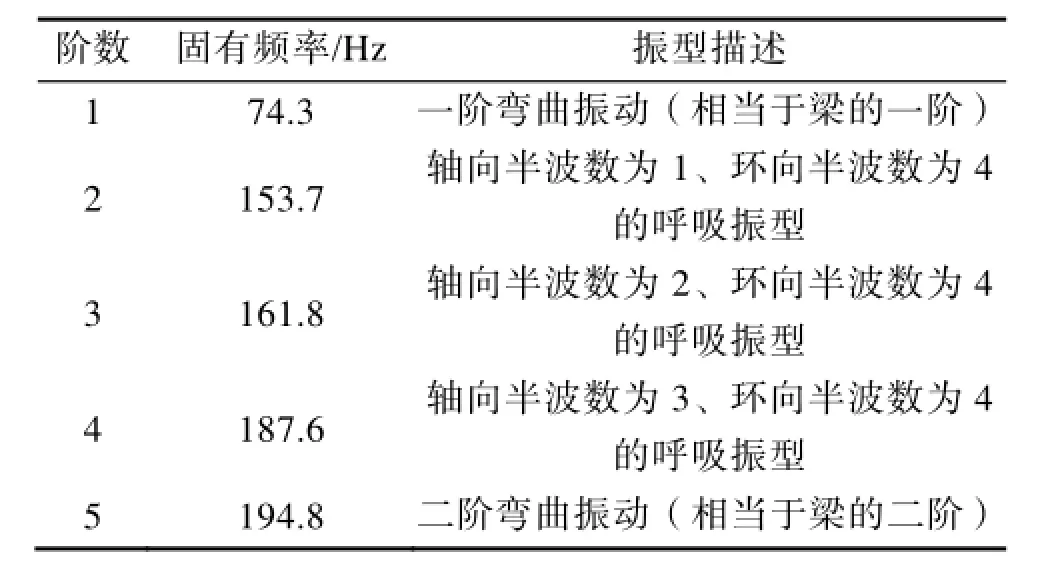
表2 自由状态下试件的固有频率Table 2 The natural frequency of the specimen in free state

图5 自由状态下的模态振型Fig.5 The mode shapes of the sepcimen in free state

3.2 地面试验系统

利用试件、支架的有限元模型，采用节点对应重合的连接方式建立了地面试验系统的有限元模型，建立试验台整体的有限元模型如图6所示，有限元计算与实测试验系统的固有频率比较见表3，有限元分析得到的整体前四阶振型如图所示。

由于试验中前两阶的刚体运动振型无法在有限元分析中得到，其余振型都能在有限元分析中得到，且有限元分析得到的固有频率与实验值相比，相对误差最大为6.76%，满足工程要求。由于结构较大，模态实验测点分布相对稀疏，实验只能得到前六阶振型，若要得到更多振型，应对测点布局加密。

图6 地面试验系统的有限元模型Fig.6 The finite element model of the ground test system

表3 地面试验条件下试件实测与有限元计算固有频率的比较Table 3 Comparison of the natural frequency of the test specimen and the finite element calculation under the ground test condition

图7 平台有限元分析前四阶振型Fig.7 The preceding four mode shapes of the system in finite element analysis

4　响应预示与试验载荷的获取

在模拟件尾端施加振动激励，根据结构响应进行聚类分析，确定了模拟件端部某点作为预示点，如图8所示。针对该模拟件结构，构造振动激励数据集，某振动激励谱型如图9所示，计算模拟件预示点在飞行状态及地面试验状态下的振动加速度响应。

图8 基于聚类分析确定的预示测点Fig.8 The prediction point based on clustering analysis

图9 振动激励力谱型Fig.9 The spectrum of the vibration excition force

根据振动响应数据及构造学习样本，采用机器学习的方法建立映射关系模型。然后，依据地面试验设计所得到的振动响应作为输入样本，输入到映射关系模型即可得到飞行状态下的振动响应，并与飞行状态计算所得的振动响应进行比较，实现振动响应映射预示方法的仿真验证。

基于30组振动激励数据，选取25组进行映射关系模型的建立，其他未参与学习的5组数据进行预示与验证。将试验状态的响应数据输入到映射关系模型，得到飞行状态下对应测点的振动响应预示结果，并与计算得到的飞行状态下的振动响应进行对比，结果如图10所示，预示结果与计算结果基本吻合。

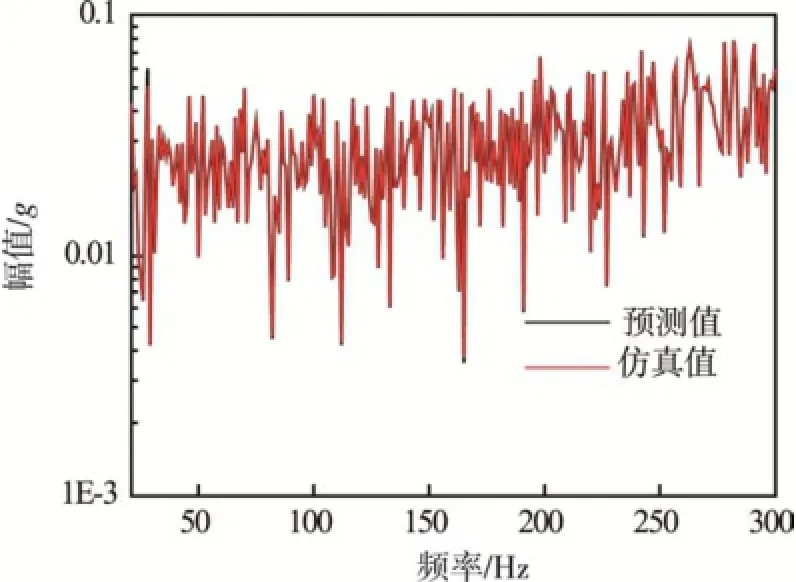
图10 由试验状态预示飞行状态的响应Fig.10 The response of the flight state is indicated by the test condition

另外，若已知飞行状态的遥测数据，如图 11所示，将该遥测振动响应作为工作样本，输入到映射关系模型，得到地面试验状态的振动响应，如图12所示。那么，基于载荷反求可确定施加在模拟件尾部的激励力谱型，如图13所示。

图11 飞行状态振动响应遥测数据Fig.11 The vibration response telemetry data in flight state

图12 根据天地映射确定的地面状态振动响应数据Fig.12 The vbiration response data in ground state determined by mapping relation

图13 基于载荷反求确定的地面试验激励力谱型Fig.13 The ground test excitation spectrum based on load identification

映射关系模型代表了被研究结构的固有特性，当建立该模型时需要利用受两种不同边界约束的被研究结构的响应，要求建立的模型正确，并给系统1和系统2施加相同的载荷。为了能充分反映系统1和系统2的特征，施加到系统1和系统2模型上的载荷的类型应为平谱，且载荷的范围足够大。

5　结语

提出天地数值计算-地面试验验证联合法，通过映射关系模型将飞行和地面试验环境下结构的振动响应有机地结合起来，在不需要模拟飞行状态边界条件的情况下，完成地面模拟试验。以细长体结构为例，实现了计算和试验的全过程，证明了该方法的可实施性。

[1] GJB 150A—2009, 军用装备实验室环境试验方法[S]. GJB 150A—2009, Laboratory Environmental Test Methods for Military Materiel[S].

[2] MIL-STD-810G, Environmental Engineering Considera-tions and Laboratory Tests[S].

[3] MIL-STD-1540C, Test Requirements Launch Upper-stage Space[S].

[4] 闫桂荣, 董龙雷, 喻磊. 基于机器学习动力学环境的预示方法[J]. 应用力学学报, 2013, 30(1): 13—18. YAN Gui-rong, DONG Long-lei, YU Lei. A New Dynamical Environment Predication Method Based on Machine Learning[J]. Chinese Journal of Applied Mechanics, 2013, 30(1): 13—18.

[5] 毛文涛. 支持向量回归机模型选择研究及在综合力学环境预示中的应用[D]. 西安: 西安交通大学, 2011. MAO Wen-tao. Research on Model Selection for Support Vector Regression and Its Application in Prediction of Combined Dynamics Environment[D]. Xi'an: Xi'an Jiaotong University, 2011.

[6] MAO Wen-tao, HU Di-ke, YAN Gu-irong. A New SVM Regression Approach for Mechanical Load Identification[J]. International Journal of Applied Electromagnetics and Mechanics, 2010, 33(3/4): 1001—1008.

[7] MAO Wen-tao, YAN Gui-rong, DONG Long-lei. Weighted Solution Path Algorithm of Support Vector Regression Based on Heuristic Weight-setting Optimization[J]. Neurocomputing, 2009, 73(1—3): 495—505.

[8] 王成, 焦吉祥, 黄翔龙, 等. 基于一元线性回归模型的多源频域载荷识别[C]// 第八届全国随机振动理论与应用学术会议暨第一届全国随机动力学学术会议论文集.成都: 西南交通大学, 2012: 848—854. WANG Cheng, JIAO Ji-xiang, HUANG Xiang-long, et al. A Multi-sources Load Identification Algorithm in Frequency Domain Based on Linear Regression[C]// International Conference on Theory Application of Random Vibration. Chengdu: Southwest Jiaotong University, 2012: 848—854.

[9] VAPNIK V N. Estimation of Dependences Based on Empirical Data[M]. Berlin: Springer, 1982.

[10] VAPNIK V N. The Nature of Statistical Learning Theory[M]. Berlin: Springer, 1995.

[11] CHERKASSKY V, MULIER F. Learning from Data: Concepts, Theory and Methods[M]. New York: John Viley& Sons, 1997.

[12] MJOLSNESS E, DECOSTE D. Machine Learning for Science: State of the Art and Future Prospects[J]. Science, 2001, 293(14): 2051—2055.

[13] 张学工. 关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1): 32—42. ZHANG Xue-gong. Introduction to Statistical Learning Theory and Support Vector Machine[J]. Chinese Journal of Automation, 2000, 26(1): 32—42.

[14] 邓乃扬, 田英杰. 数据挖掘中的新方法——支持向量机[M]. 北京: 科学出版社, 2006. DENG Nai-yang, TIAN Ying-jie. New Methods in Data Mining—Support Vector Maching[M]. Beijing: Science Press, 2006.

[15] 王彦飞. 反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007. WANG Yan-fei. Computational Methods Inverse Problems and Their Application[M]. Beijing: Higher Education Press, 2007.

A Method and Its Application for Improving the Validity of Ground Testing of Mechanical Environment's Effects on Aircraft Structure

YAN Gui-rong, DONG Long-lei, SONG Li-qiang
(State Key Laboratory for Strength and Vibration, Xi'an Jiaotong University, Xi'an 710049, China)

Objective To study the way of improving the validity of the aircraft structure ground test. Methods The finite element models of the specimen structure in flight and ground test conditions were calculated. Then the test model of the specimen structure in ground testing was measured to verify the validity of the finite element model. The vibration response of feature points in flight and ground testing was calculated. The mapping relation model of the feature points was calculated by machine learning methods. Then the response of each point in ground testing was determined by flight point response (or telemetry data) and their equivalent load was obtained by load reverse method. Finally, the load imposed on the test system was determined. Results With a slender body structure as an example, the maximum relative error between the finite element model and the measured model of the test system was 6.76%. The vibration response of the feature points in flight state could be predicted via mapping relation model. The vibration response of the cor-responding ground testing points could be determined. The load to be applied was set at 60 N by reverse deliberation according to response points of ground test system. Conclusion By the unified method of the flight-ground numerical calculation and the ground testing, the load to be applied in the ground test can be determined without deliberately simulating the boundary conditions in flight state, which improves the validity of the aircraft ground testing.

vibration test; mapping relation model; finite element analysis; test validity

2016-08-12；Revised：2016-08-29

10.7643/ issn.1672-9242.2016.05.002

TS206

A

1672-9242(2016)05-0010-07

2016-08-12；

2016-08-29

国家自然科学基金项目（10276032）

fund program：National Natural Science Foundation of China（10276032）

阎桂荣（1942—），女，陕西西安人，教授，主要研究方向为复合动力学环境仿真与控制、振动控制、现代力学测控理论与技术等。

Biography：YAN Gui-rong （1942—）， Female， from Xi'an， Shanxi， Professor， Research focus: environmentdynamic simulation & control，theory andtechnology of vibration measure & control.