结构振动疲劳加速试验技术研究

蒋瑜，陶俊勇

（国防科技大学 机电工程与自动化学院 装备综合保障技术重点实验室，长沙 410073）

结构振动疲劳加速试验技术研究

蒋瑜，陶俊勇

（国防科技大学 机电工程与自动化学院 装备综合保障技术重点实验室，长沙 410073）

目的 提出一种用于评估随机振动环境下工程结构长期耐久性和疲劳可靠性的加速试验技术。方法 通过开展一系列高斯和非高斯振动疲劳对比试验，系统研究影响结构振动疲劳寿命的各种因素，包括随机振动激励的均方根值、功率谱密度、带宽和峭度值等。结果 非高斯随机振动激励的带宽和峭度值对结构振动疲劳寿命也有明显影响。结论 当结构振动激励呈现明显的非高斯特征时，设计随机振动疲劳加速试验方案必须综合考虑振动激励的带宽和峭度值。

非高斯；随机振动；振动疲劳；加速试验

振动引起的疲劳问题严重危及重大装备及结构的可靠性和安全性。如果能够提前准确预测结构的振动疲劳寿命，就能在发生灾难性事故之前及时预知并采取相应的措施，并可为其定寿、延寿提供科学的依据，最大限度地发挥装备效益。随着结构可靠性水平的提高，结构的振动疲劳寿命越来越长，为了能够在实验室验证其寿命是否达到设计要求，振动加速试验成为必然的选择，而系统掌握影响结构振动疲劳的因素是科学开展振动加速试验的前提。

结构振动疲劳问题涉及结构动力学、随机振动学以及疲劳断裂学等多个学科。虽然振动疲劳问题早在工程实际中广泛存在，但有关振动疲劳加速试验的系统研究迄今仍然处于探索阶段。G.Allegri研究了适用于平稳宽带高斯随机振动加速试验的逆幂律模型[1]。Martin研究了在振动疲劳加速试验中如何跟踪结构共振频率和阻尼的变化以实现全过程常幅值加载，所用的载荷是正弦激励[2]。G.J. Yun开发设计了一套用于快速获取航空用铝合金材料疲劳特性曲线的高周共振疲劳加速试验闭环控制系统，所用载荷也是正弦激励[3]。Ashwiniy研究了附着不同阻尼材料的铝合金梁在高斯随机振动加速试验中的疲劳寿命差异，探讨了结构阻尼对振动试验加速因子的影响[4]。南京航空航天大学姚卫星课题组对振动疲劳做了较系统的研究，提出了时域振动疲劳寿命估算样本法，讨论了结构阻尼和频率对振动疲劳寿命的影响[5]。王冬梅对振动加速试验的逆幂律模型进行了推导[6]。李奇志提出通过试验的方式获得振动试验的加速因子[7]。朱学旺等应用基于窄带模型的修正方法得到了宽带随机振动试验加速因子计算的通用表达式[8]。

当前工程中进行振动疲劳分析时，通常假设结构承受的随机载荷符合平稳高斯分布[9—10]，但在实际环境中，许多随机载荷往往呈现比较明显的非高斯特征，尤其是在工况恶劣或者极端环境下[11—12]。近年来的研究表明，非高斯特性对结构振动疲劳有着不可忽视的影响[13—15]。目前国内外相关研究主要停留在理论研究，实际开展的振动疲劳加速试验研究不多，很少系统考虑振动激励的各种特性参数（尤其是非高斯特性）和结构自身动力学特性对结构振动疲劳寿命的综合影响。文中将对此进一步开展系统的实际试验研究，揭示其影响规律。

1　试验设计

1.1 振动疲劳试验根据随机振动理论，系统的响应取决于振动激励和结构的动力学传递特性这两个因素。一旦结构的材料、尺寸、形状及安装固定方式确定下来，其动力学特性往往也确定了。为了保证加速试验结果的可信性，在进行加速试验时，一般会尽量保持不改变结构动力学特性，往往通过改变随机振动激励的一些特性来取得加速效果。因此在进行试验设计之前，首先要搞清楚完整描述随机振动激励的参数有哪些。

最常见用来描述随机振动的参数是PSD，但是实际上 PSD并不能充分刻画随机振动的全部特性。比如具有相同功率谱密度和均方根的随机振动信号可以具有完全不同的幅值概率密度分布特性，如图

1所示。由于高斯随机过程二阶以上的高阶统计量恒为0，所以仅用功率谱密度函数或自相关函数就能完整表征。对非高斯随机过程的完整描述除了功率谱密度函数，还需要借助二阶以上的高阶统计量进行补充描述。工程上常用偏斜度S和峭度 K这两个参数来描述非高斯随机过程 X，定义为：

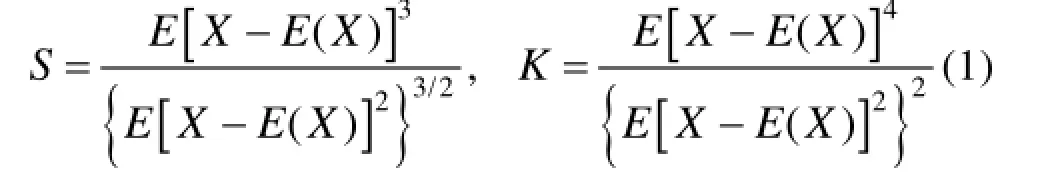
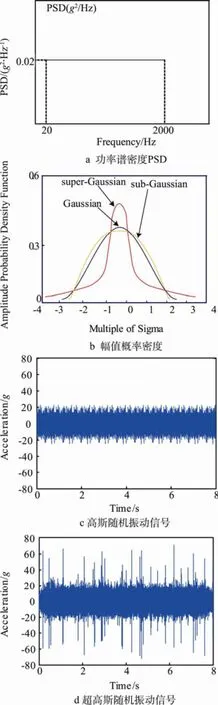
图 1 具有相同功率谱密度的高斯和超高斯随机振动信号Fig.1 Gaussian and super-Gaussian vibration signals with the same PSD

高斯随机过程的偏斜度值等于0，峭度值等于3；而非高斯随机过程的峭度值肯定不等于 3，偏斜度值可以等于0，也可以不等于0。偏斜度用来描述随机过程幅值概率密度曲线偏离对称分布的程度，偏斜度值不为0表示服从非对称分布。峭度是描述随机过程幅值概率密度曲线拖尾分布特征的参数，它不仅可用来区分高斯和非高斯随机过程，而且还可进一步将非高斯随机过程区分为亚高斯和超高斯随机过程，其中亚高斯随机过程的K<3，超高斯随机过程的K>3。工程中常见的非高斯振动信号往往是具有尖峰分布的超高斯信号。

综上所述，完整描述随机振动激励的五个重要参数分别是：均方根值、功率谱密度、功率谱带宽、峭度值和偏斜度值。由于工程中以及实验室模拟的大多数振动信号往往是对称分布的，所以文中重点考察前四个参数对振动疲劳损伤累积的影响，为此设计了如下四组振动疲劳试验方案（为简便起见，功率谱密度曲线的谱形均采用平直谱），见表1—4。

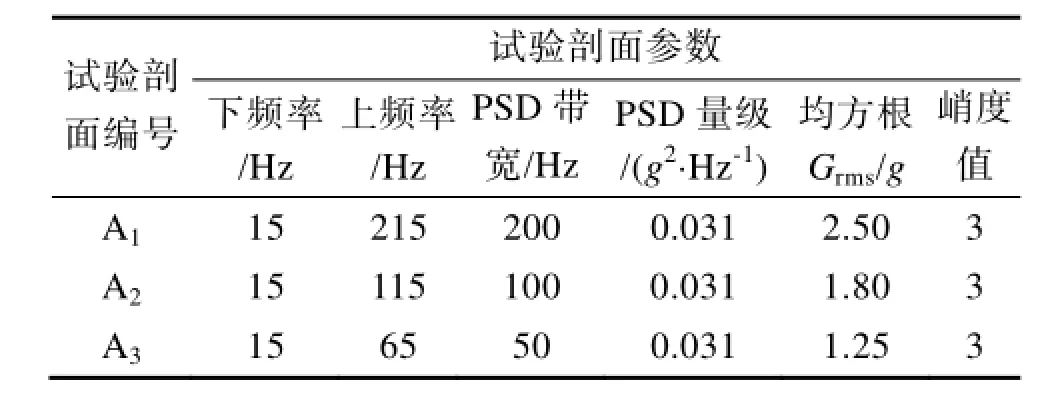
表 1 试验组ATable 1 Group A

A组的试验目的是考察高斯随机振动激励的均方根值和带宽对振动疲劳的影响。

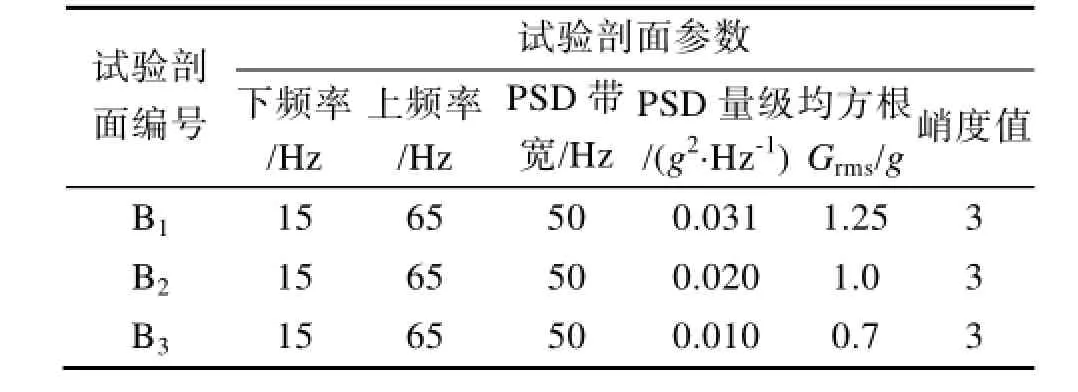
表 2 试验组BTable 2 Group B

B组的试验目的是考察高斯随机振动激励功率谱密度量级大小对振动疲劳的影响。

C组的试验目的是考察非高斯随机振动激励的峭度值对振动疲劳的影响。

D组试验目的是考察非高斯随机振动激励的带宽对振动疲劳的影响。

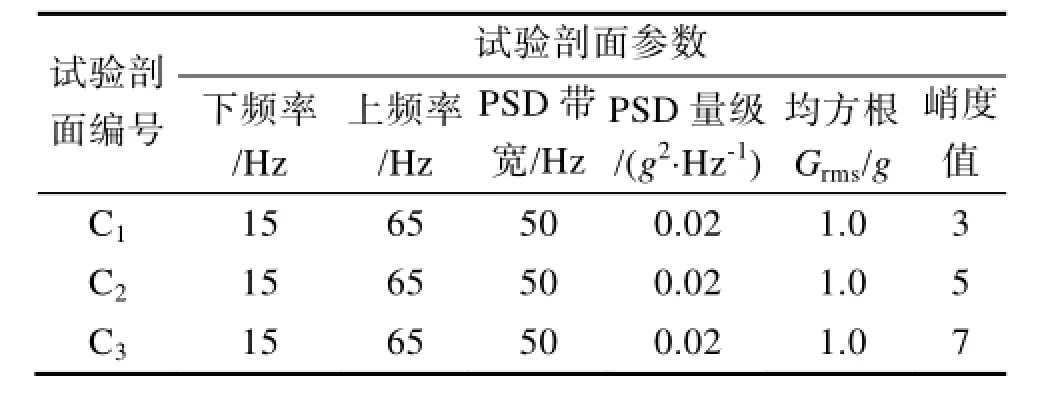
表 3 试验组CTable 3 Group C

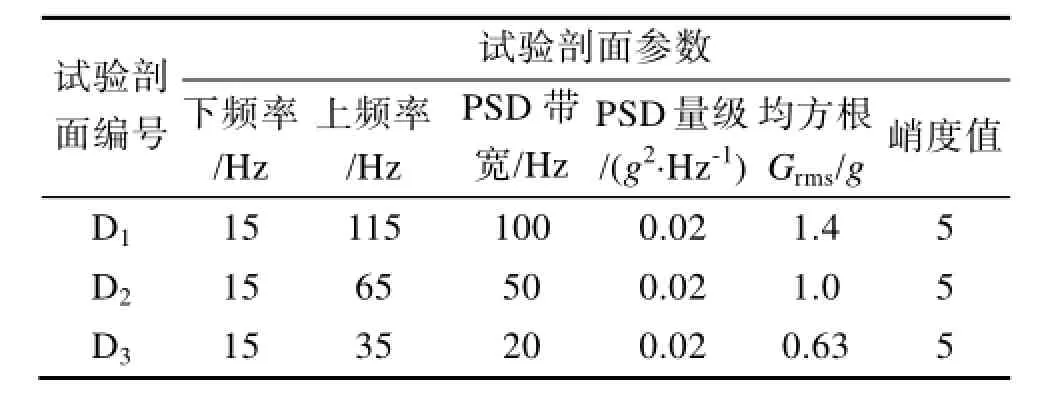
表 4 试验组DTable 4 Group D

可以看出，在每相邻两组试验中，有一个试验剖面参数是相同的，比如 A3和B1、B2和 C1、C2和 D2。这样设计的好处是可以充分利用前一组试验的数据进行对比分析，并可大大减少试验总次数和样本量。

1.2 振动疲劳试验系统

振动疲劳试验系统由振动台、功率放大器、振动控制器、加速度计等组成。其中振动控制器型号为国防科技大学可靠性实验室自主开发的非高斯随机振动控制系统 NRVCS，该控制器除了能够进行传统的正弦、高斯随机和冲击等试验外，还能产生具有指定功率谱密度和峭度值的非高斯随机激励信号，能够用于研究非高斯随机振动疲劳。振动台是Brüel & Kjær公司的V406系列，最大加速度可以达到100g，频率范围为5～9000 Hz。两个加速度计型号均为Dytran公司的3030B4系列，一个用于提供反馈信号给控制器，一个用于监测试件振动响应，灵敏度分别为9.86，9.71 mV/g。

1.3 试件和夹具设计

为了在有限的时间内完成振动疲劳试验，设计了如图2和3所示带缺口的试件及配套夹具。试件一端的四个小孔用于将其安装固定在振动台台面上；另外一端也设计有两个孔，一个用于安装附加的质量块以加快振动疲劳失效进程，另外一个用于安装加速度计以测试试件的振动响应特性。试件材料为Al 6061-T6 合金，由于其优良的机械力学特性而被广泛应用于航空航天、机械零件、结构工程等领域。

图 2 试件和夹具Fig.2 Fixture and specimen

图3 测量应力的应变片Fig.3 Strain gage

采用Vishay公司生产的Micro-Measurements-&SR-4通用应变片来测量试件在危险点，即缺口处的应变信号，从而获得动态应力响应。应变片的阻值为（350±2）Ω，Gage Factor为2.125±0.010。应变片以1/4电桥的形式安装在试件上，应变计的三条引线通过 RJ45接口连接到应变仪 Model 8000-8-SM的输入端。高精度应变仪Model 8000-8-SM由Vishay公司下属的Micro-Measurem- ents生产，用于对应变信号进行采集分析和处理。该应变仪采用网络接口与主机上的 StrainSmart测量应用软件进行通讯，可以同时进行8通道应变信号的采集分析，每通道采样频率有 1000/500/200/100/10 Hz五档可选，最高可达1 kHz。该应变仪具有自校准功能，应变测量范围最高可达+/-310000 με，测量分辨率最高可达0.5 με。根据上述试验设计，最终搭建的整个试验现场如图4所示。

图4 振动疲劳试验现场Fig.4 Experimental setup for accelerated vibration fatigue test

2　结果和讨论

试验中破坏的试件如图5所示，详细的试验结果见表5。

图5 发生疲劳断裂失效的试件Fig.5 Fatigue broken specimens

从A组试验结果看，尽管A1，A2，A3的均方根值和带宽均不同，但是由于功率谱密度在结构一阶固有频率处的量级一样，试验结果都比较接近，没有明显的差异。这说明对结构随机振动疲劳来说，只要结构的一阶固有频率在激励频带内，并且高斯随机振动激励的功率谱密度在结构一阶固有频率处的量级保持一致，高斯随机振动激励的带宽和均方根值对振动疲劳寿命影响很小。这个比较容易理解和解释，因为结构随机响应的大小主要取决于激励在结构共振频率点上的能量分布。

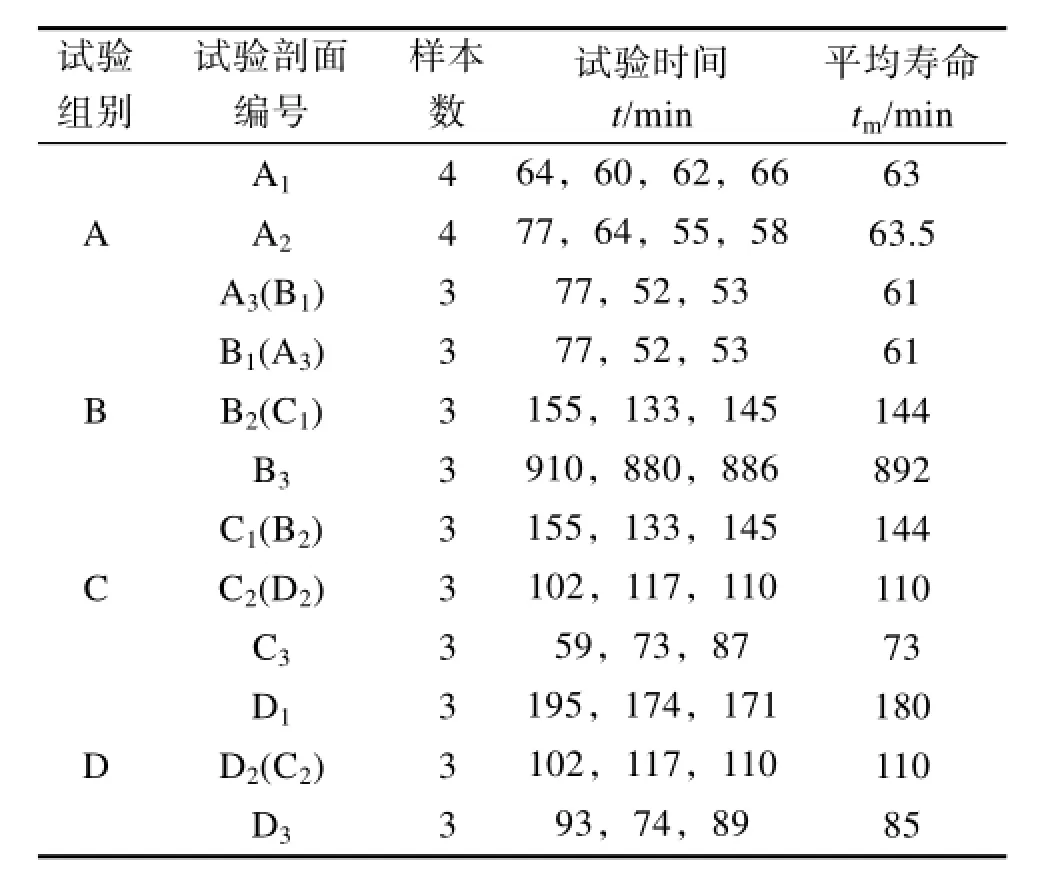
表5 振动疲劳试验结果Table 5 Vibration fatigue test results

B组的试验结果进一步验证了上述规律。B1，B2，B3的带宽一致，但是通过改变高斯随机振动激励的功率谱密度在结构一阶固有频率处的量级大小，来改变激励的均方根值，从而使得结构的振动疲劳寿命也发生了显著的改变。

C组的试验结果表明，超高斯随机振动激励的峭度值对结构振动疲劳寿命也有显著的影响。在同样功率谱密度和均方根值的条件下，超高斯随机振动激励的峭度值越高，结构振动疲劳寿命越短。

D组试验结果表明，超高斯随机振动激励的带宽对结构振动疲劳寿命也有显著的影响。在同样峭度值和同样功率谱密度量级的条件下，超高斯随机振动激励的带宽越小，结构振动疲劳寿命越短。

3　结论

文中搭建了一套随机振动疲劳试验系统，通过精心设计振动疲劳试验方案，系统考察了影响结构振动疲劳寿命的各种因素，得到以下结论：

1) 对高斯随机振动，影响结构振动疲劳寿命最大的因素是高斯随机振动激励的功率谱密度在其一阶固有频率处的量值；而高斯随机振动激励的均方根值、带宽等因素对结构振动疲劳寿命影响很小。

2) 对非高斯随机振动，除了非高斯随机振动激励的功率谱密度在结构一阶固有频率处的量值，非高斯随机振动激励的带宽和峭度值对结构应力响应的非高斯特性均有显著影响，从而对结构振动疲劳寿命也有明显影响，在设计振动加速试验方案时需要综合考虑。

[1] ALLEGRI G, ZHANG X. On the Inverse Power Laws for Accelerated Random Fatigue Testing[J]. Int J Fatigue, 2008, 30(6): 967—977.

[2] MARTIN C, JANKO S, MIHA B. Uninterrupted and Accelerated Vibrational Fatigue Testing with Simultaneous Monitoring of the Natural Frequency and Damping[J]. Journal of Sound and Vibration, 2012, 331(24): 5370—5382.

[3] YUN G J, ABDULLAH A B M, BINIENDA W. Development of a Closed-loop High-cycle Resonant Fatigue Testing System[J]. Exp Mech, 2012, 52(3): 275—288.

[4] ASHWINI P, ABHIJIT G, GURU R K. Fatigue Failure in Random Vibration and Accelerated Testing[J]. Journal of Vibration and Control, 2012, 18(8): 1199—1206.

[5] 王明珠. 结构振动疲劳寿命分析方法研究[D].南京: 南京航空航天大学, 2009. WANG Ming-zhu. Research on Life Analysis Method for Structure Vibration Fatigue[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.

[6] 王冬梅, 谢劲松. 随机振动试验加速因子的计算方法[J]. 环境技术, 2010, 28(2): 47—51. WANG Dong-mei, XIE Jin-song. Acceleration Factor Calculation Method of Random Vibration Test[J]. Environment Technology, 2010, 28(2): 47—51.

[7] 李奇志, 陈国平, 王明旭, 等. 振动加速因子试验方法研究[J]. 振动、测试与诊断, 2013, 33(1): 35—39. LI Qi-zhi, CHEN Guo-ping, WANG Ming-xu, et al. Test Method of Vibration Acceleration Factor [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(1): 35—39.

[8] 朱学旺, 张思箭, 宁佐贵, 等. 宽带随机振动试验条件的加速因子[J]. 环境技术, 2014, 32(6): 17—20. ZHU Xue-wang, ZHANG Si-jian, NING Zuo-gui, et al. Accelerated Testing Factor on Wideband Random Vibration[J]. Environment Technology, 2014, 32(6): 17—20.

[9] 刘凯. 基于实测数据的空空导弹自由飞振动条件制定方法研究[J]. 装备环境工程, 2014, 11(5): 114—118.LIU Kai. Study on the Method of Making Free Flight Vibration Profile for Air-to-Air Missile Based on Measured Data[J]. Equipment Environmental Engineering, 2014, 11(5): 114—118.

[10] 蔡健平, 张萌, 赵婉. 装备典型舰载平台振动环境严酷度分析[J]. 装备环境工程, 2015, 12(1): 87—92. CAI Jian-ping, ZHANG Meng, ZHAO Wan. Severity Analysis of Typical Shipboard Vibration Environment for Materiel[J]. Equipment Environmental Engineering, 2015, 12(1): 87—92.

[11] JIANG Yu, TAO Jun-yong, WANG De-zhi. Simulation of Non-gaussian Stochastic Processes by Amplitude Modulation and Phase Reconstruction[J]. Wind and Structures, 2014, 18(6): 693—715.

[12] MIL-STD-810G, 环境工程考虑和试验室试验[S]. MIL-STD-810G, Test Method Standard for Environmental Engineering Considerations and Laboratory Tests[S].

[13] 蒋瑜. 频谱可控的超高斯随机振动环境模拟技术及其应用研究[D]. 长沙: 国防科学技术大学, 2005. JIANG Yu. Research on the Simulation of Super-gaussian Random Vibration Environment with Controllable Frequency Spectrum and Its Applications[D]. Changsha: National University of Defense Technology, 2005.

[14] CHENG Hong-wei, TAO Jun-yong, CHEN Xun, et al. Fatigue Reliability Evaluation of Structural Components under Random Loadings[J]. Proc I Mech E Part O: Journal of Risk and Reliability, 2014, 228(5): 469—477..

[15] 王得志. 非高斯振动环境下的装备结构可靠性研究[D].长沙: 国防科学技术大学, 2010. WANG De-zhi. Research on the Structure Reliability under Non-gaussian Vibration Environment[D]. Changsha: National University of Defense Technology, 2010.

Accelerated Vibration Fatigue Testing of Structures

JIANG Yu, TAO Jun-yong
(Science and Technology on Integrated Logistics Support Laboratory, College of Mechatronic Engineering and Automation, National University of Defense Technology, Changsha 410073, China)

Objective To develop a new technology of accelerated vibration fatigue test to assess the long-term durability and fatigue reliability of engineering structures under random vibration environment. Methods Various factors that affect the structural vibration fatigue life were systematically studied by Gaussian/non-Gaussian random vibration fatigue tests, including root mean squares, power spectral density, power spectral bandwidth and kurtosis of acceleration excitation. Results The test results showed that the kurtosis value and the bandwidth of non-Gaussian random vibration excitation also had a significant impact on the structural vibration fatigue life. Conclusion If the structural vibration excitation shows obvious non-Gaussianity, the kurtosis value and the bandwidth must be considered for the quantitative design of random vibration fatigue accelerated testing.

non-Gaussian; random vibration; vibration fatigue; accelerated testing

2016-08-02；Revised：2016-08-09

10.7643/ issn.1672-9242.2016.05.005

TJ01；TB114

A

1672-9242(2016)05-0030-06

2016-08-02；

2016-08-09

蒋瑜（1977—），男，湖北随州人，副教授，主要研究方向为振动试验技术。

Biography: JIANG Yu（1977—）， Male， from Suizhou， Hubei， Associate Professor， Research focus: vibration test.