复合材料太阳翼基板声学疲劳特性研究

郑玲，张巍，曾杰，向树红，李晔，杨江

（1.重庆大学 汽车工程学院 机械传动国家重点实验室，重庆 400044；2.北京卫星环境工程研究所，北京100094）

复合材料太阳翼基板声学疲劳特性研究

郑玲1，张巍1，曾杰1，向树红2，李晔2，杨江2

（1.重庆大学 汽车工程学院 机械传动国家重点实验室，重庆 400044；2.北京卫星环境工程研究所，北京100094）

研究航天器在声激励下的疲劳行为及其演变规律，对证航天器的运行安全。针对碳纤维蒙皮-铝蜂窝的太阳翼基板声致疲劳问题，使用耦合FE/BEM方法，建立航天器太阳翼基板的数值分析模型，以声学试验结果为依据，对仿真模型进行验证。噪声激励持续作用60 s后，损伤率分布呈沿结构长轴对称状态，疲劳危险点处最大损伤率D=0.0232，太阳翼基板未出现疲劳破坏，最短疲劳寿命T= 2.58×103s。太阳翼基板中心区域为结构设计薄弱处，该区域在多阶模态下的应力水平较高，疲劳寿命较短，极易导致疲劳破坏。

噪声激励；FE/BEM；混响；声学响应；疲劳寿命

卫星、太阳翼基板等航天器在发射及飞行过程中始终伴随着20～8000 Hz的宽频带噪声，强度可达140 dB以上。噪声作用于太阳翼基板等薄壁结构将产生动态应力响应，一定强度噪声激励所引起的交变应力可导致结构的疲劳损伤[1—2]，引起航天器结构连接处、蒙皮表面等部位疲劳破坏，严重影响航天器的安全和使用寿命。研究航天器在声激励下的疲劳行为及其演变规律，对保证航天器的运行安全具有重要意义。

对于航空航天薄壁板、蒙皮壁板等结构的声疲劳分析，工程上大多以试验为基础，按照经验公式计算出蒙皮壁板的基频和应力响应，再结合诺谟图或公式等计算结构疲劳寿命，如广泛应用的 DSR法[3]。美国波音公司[4]采用快速-DSR法，对蒙皮-腹板、蜂窝结构等进行了疲劳寿命计算。刘景光[5]等采用有限元与 DSR相结合的方法，计算了钛合金壁板的疲劳寿命，验证了计算方法的准确性。由于上述方法依赖一定的实验条件、成本较高，且运用于复合夹心板时，DSR等参数难以确定。因此，DSR方法存在一定局限性。在进行复杂结构的疲劳寿命分析时，数值分析方法成本低廉，计算效率高，广泛运用于航空航天。疲劳寿命数值分析方法分为时域估算法和频域估算法[6—8]。时域法首先对响应随机过程进行时域模拟，采用经典“雨流循环计数”从时域应力响应曲线中获取应力循环的幅值和均值及其概率分布。时域法通常能得到比较准确的累积损伤分析精度，但需要足够长的时域信号。白春玉等采用时域分析法，提出了功率谱输入和时域输入两种算法，进行白噪声激励下T形板的疲劳寿命预估，验证算法可行性。相比时域法，频域法是基于功率谱密度（PSD）的分析方法，数据处理简便。PSD函数是描述平稳各态历经过程最重要的参数，利用响应PSD函数可获得随机应力信号的分值频率、峰值概率分布和均方根值，再结合材料S-N曲线计算结构疲劳寿命。沙云东等[9]提出了基于应力概率密度和功率谱密度法的随机声疲劳寿命预估方法，对航空发动机薄壁结构进行疲劳寿命预测。Bishop[10]从雨流循环定义入手，结合Dirlik经验公式，给出了基于功率谱密度的疲劳寿命计算方法，对于工程应用有较大参考价值。在频域内进行疲劳寿命分析具有计算简便、工程适用性强的特点。

航天器太阳翼基板主要采用碳纤维-铝蜂窝夹层结构。基板芯层为正六边形铝蜂窝，面板一般由碳纤维复合材料制作的空心网格层铺设而成。为满足不同区域的强度和刚度需求，面板不同区域需要设计不同铺层数、铺层方向，从而形成了复杂的非连续铺层。太阳翼基板复杂的结构设计满足了轻量化和高强度等需求，但也为准确的响应计算和疲劳寿命分析带来较大难度。杨江[11]等分别基于FE-SEA混合方法和耦合FE/BEM方法建立了太阳翼基板仿真模型并进行结构响应计算，预示的响应与噪声试验结果基板对应，但该方法不能直接运用于疲劳寿命分析。刘捷[12]等建立了蜂窝夹层结构天线罩的有限元模型，从中剥离各典型结构及其边界条件作为试验依据，采用试验方法研究该结构声疲劳特性，结果表明蜂窝是疲劳破坏的关键。该方法准确性较高，但是成本也相对较高。建立精确的动力学模型和疲劳寿命预测方法是复合太阳翼基板疲劳寿命研究的难点。

文中采用“三明治夹心板”等效理论，首先对碳纤维蒙皮-蜂窝铝芯太阳翼基板进行力学等效处理。以此为基础，建立碳纤维蒙皮-蜂窝铝芯太阳翼基板有限元/边界元（FE/BEM）仿真模型，分析研究其在声激励环境下的结构响应以及疲劳寿命，为太阳翼基板等航天器构件地面声学试验条件的制定及疲劳寿命预测提供科学依据。

1　复合材料太阳翼基板的力学等效

1.1 三明治等效板理论

国内外常用的蜂窝复合夹心板的等效方法有等效板理论、蜂窝板理论、三明治夹心板理论，胡玉琴[13]总结了国内外蜂窝复合夹心板的等效模型，对以上三种等效方法进行了计算与验证。结果表明，三明治夹心板等效理论直接模拟夹层板结构，在力学性能、振动特性方面和理论值最接近，最准确地反应出结构的真实情况。

三明治等效板理论认为铝蜂窝夹层板是由上下各向同性的面层和中间各向异性的夹心所组成，其核心是通过有限元分析的方法计算夹层板，对夹层板进行数值分析。该理论假定芯层能抵抗横向剪切变形，并且具有一定的面内刚度，上、下蒙皮层服从Kirchhoff假设，忽略其抵抗横向剪应力的能力，则蜂窝芯层可以等效为一均质的厚度不变的正交异性层，较为真实地反映夹层板的结构。

1.2 太阳翼基板的力学等效

文中研究对象为太阳翼基板，蒙皮为碳纤的蜂窝铝夹心材料。根据三明治夹心等效理论，将夹心板芯层等效为正交各向异性材料，其几何参数保持不变，同时上下面板参数不变，如图1所示。

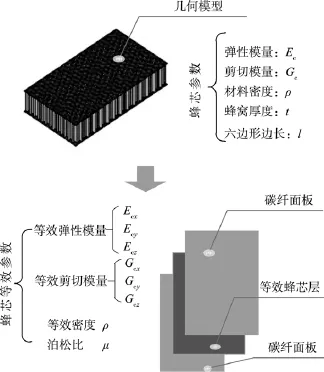
图1 太阳翼基板模型等效Fig.1 Equivalent schematic diagram in sandwich solar panel

对于正六边形胞元的蜂窝，等效为均匀层后弹性常数与蜂芯材料参数的关系为：

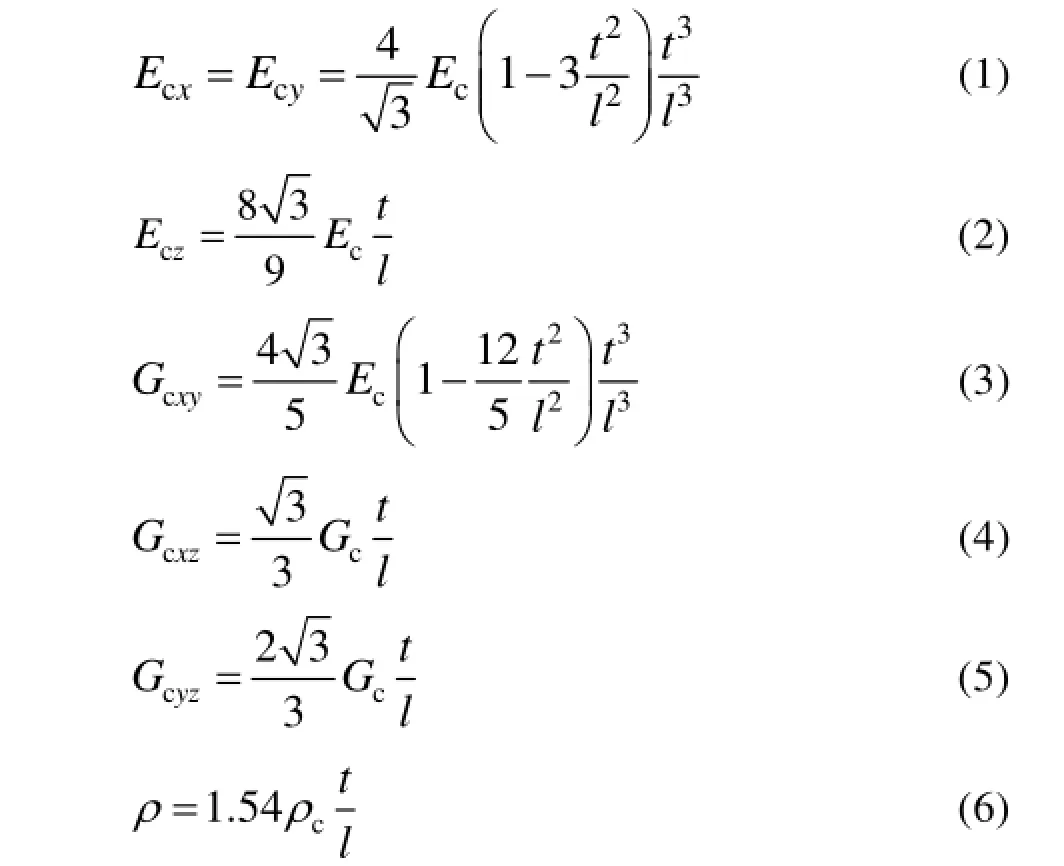
式中：ρc，Ec，Gc分别为芯子材料的密度、弹性模量与剪切模量，即铝材料参数。Ec表示蜂芯弹性模量，下标x/y/z表示蜂芯层的三个轴向，其中z向垂直于蜂芯层大平面，剪切模量下标也具有同样含义；t，l分别为芯子片的厚度和正六边形的边长。等效后蜂芯层参数见表1。

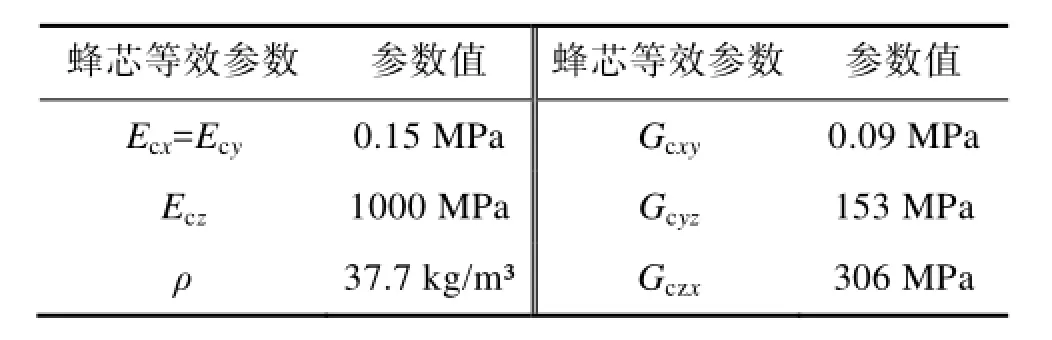
表1 蜂芯等效参数Table1 Equivalent parameters of the core in sandwich solar panel

2　复合材料太阳翼基板FE/BEM模型

2.1 FE/BEM模型

首先建立碳纤维蒙皮-蜂窝铝芯太阳翼基板有限元/边界元（FE/BEM）模型。声学边界元和结构有限元的耦合，可建立其耦合矩阵：

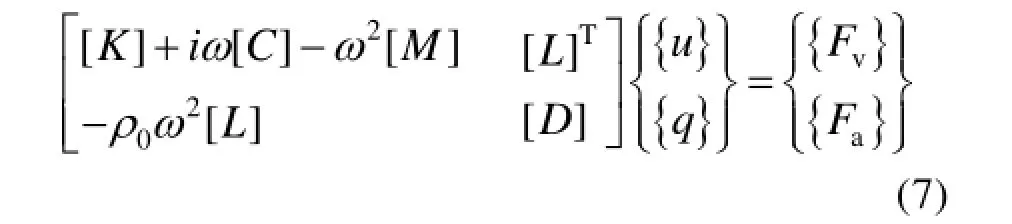
式中：[K]，[C]，[M]分别为结构刚度矩阵、阻尼矩阵和质量矩阵；{q}为节点压力向量；{u}为节点位移；{Fv}为结构载荷向量；{Fa}为流体的载荷向量；[L]为声学边界元和结构有限元耦合矩阵。

将太阳翼基板视为不同材料的铺层结构，蜂芯可简化为正交各向异性材料。采用复合层结构的铺层定义方法，建立太阳翼基板有限元模型，不同颜色区域表示不同的铺层角度及厚度，如图2所示。根据不同铺层区域和承受载荷情况，确定网格大小，其总单元数量为 5245。在声学激励条件下，其边界条件为自由状态，五个测点A1—A5分布与试验条件完全一致。

图2 太阳翼基板有限元模型Fig.2 Finite element model of composite solar panel

2.2 FE模型的验证

为了改善太阳翼基板的声学响应以及疲劳寿命预示的精度，采用太阳翼基板的声学激励响应试验结果，对太阳翼基板的有限元模型参数进行修正，有限元模型参数修正的流程如图3所示。

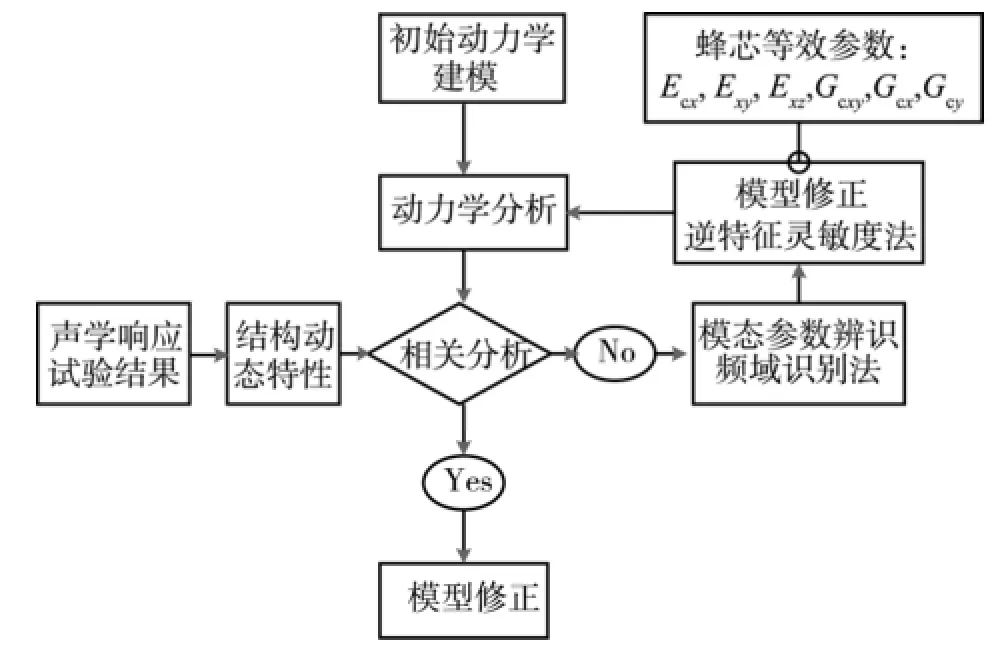
图3 模型修正流程Fig.3 Model verification chart

依据航天器动力学模型试验验证技术和参数修正流程，具体步骤如下：

1）采用FE/BEM方法建立太阳翼基板的初始模型，进行随机声学响应分析，获得结构的加速度响应PSD及动态特性。

2）进行太阳翼基板在噪声激励下的声学试验，提取结构加速度响应PSD及动态特性。

3）采用模态置信准则（MAC）评价有限元分析结果与试验结果的一致性，即相关分析。其中：

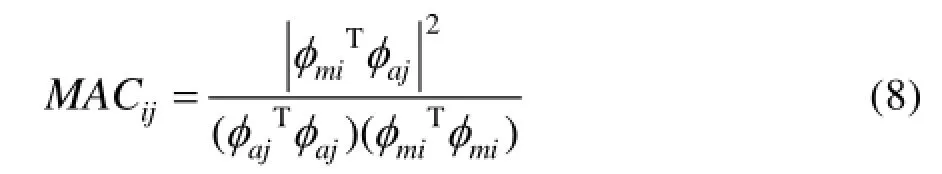
4）当相关分析不合格时，对仿真数据进行频域模态参数识别，确定对结构响应贡献较大的模态为主模态，主模态为模型修正主要参考因素。

5）采用参数法进行模型修正，最小化分析模型与实际机构在噪声激励下的响应偏差。修正量选择蜂窝芯层等效参数 Ecx，Ecy，Ecz，Gcxy，Gcyz和Gczx，采用逆特征灵敏度法确定影响结构模态的主要修正量。响应偏差为响应峰值和峰值频率。

6）模型修正后再返回步骤1），直至相关分析符合要求。

模型经参数修正后，仿真结果与实验结果基本对应。考虑结构对称性，选取一个基板外围测点A2和一个中心区域测点 A5来分析，如图 4所示。可以看出，实验与仿真得到的响应数据在峰值、峰值频率基本对应。中低频段的仿真值在峰值和变化趋势上和实验值重合较好，在高频段仿真值略大于实验值，主要原因是太阳翼基板在高频的模态密度较大，有限元/边界元法计算精度有所下降。

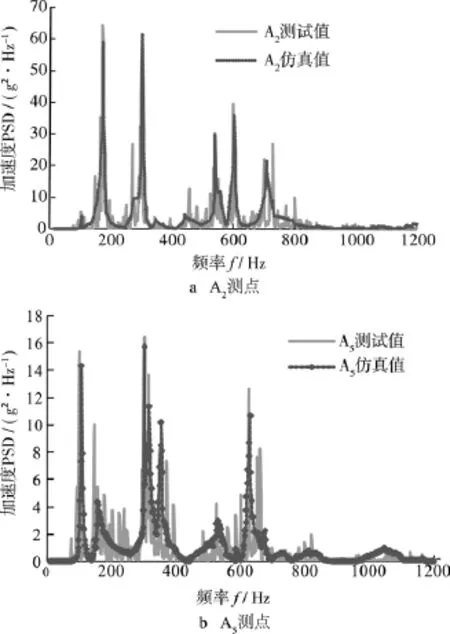
图4 修正模型后试验与仿真加速度响应功率谱峰值频率Fig.4 Comparison between experimental and numerical acceleration responses

3　声学疲劳寿命分析

3.1 声学激励下的结构响应

采用模态叠加法，计算复合材料太阳翼基板在声学激励下的结构响应。在声学激励下的局部应力可通过以式（9）计算：

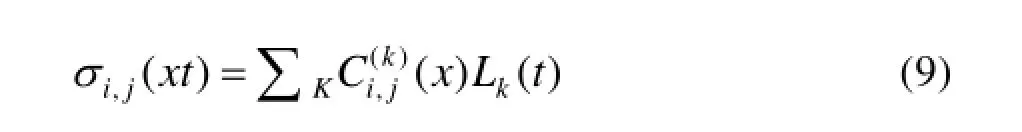
不同粗细度麸皮、全麦粉以及面粉粒径的测定结果见表 2。由表可知大、中、小三种不同粗细度麸皮的D50值分别为285.0、186.7、75.7 µm，粒径依次减小，D10和D90值也表现出相同趋势。比较同一样品的D10、D50和D90值，不难发现经旋风磨粉碎的麸皮，粒径分布范围较大，这与以往的研究相一致。可能是由于麸皮中的不同组分机械强度存在较大差异，特别是麸皮的外层果皮质地非常坚硬，因此粉碎困难。随着麸皮粒径的减小，全麦粉粒径降低，但下降程度不如麸皮明显，这主要是因为全麦粉中比例较高的面粉组分对平均粒径影响更大。含有小粒径麸皮的全麦粉与面粉粒径分布及其平均值最为接近。

根据给定的试验条件，使用多个平面波模拟混响声源，如图5所示。试验声压谱见表2，太阳翼基板处于自由状态。

图5 混响声源Fig.5 Reverberation sound source

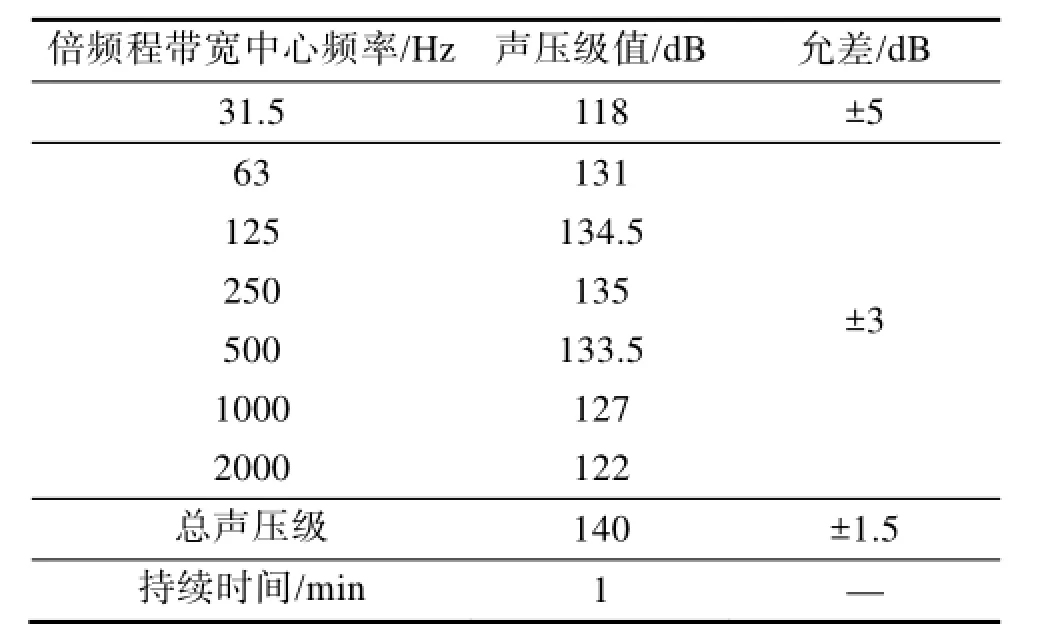
表2 试验声压谱Table 2 Sound pressure spectrum in test

图6是通过模态分析，获得的太阳翼基板模态应力分布。根据式（9）可计算太阳翼基板在噪声激励下的应力响应。

图6 前六阶模态应力Fig.6 Modal stress distribution of the first six modes

3.2 疲劳损伤理论

在典型结构的使用寿命区间，零件通常受到周期性载荷的作用，其载荷可能是常幅的，也可能是变幅的。如果加载振幅随时间变化，一个循环的构成及响应的振幅则更加难以确定。根据应力、应变、力等加载参数的时间历程，可以对循环进行计数，将复杂的变幅加载历程简化为一组离散的简单常幅加载过程。雨流计数法被认为是预测疲劳寿命的较好方法。对于随机激励这种复杂载荷，雨流计数可以识别在复杂载荷序列中与常幅疲劳数据相似事件，并筛选去掉应力幅值较小的事件。在随机噪声激励下，采用雨流计数法筛选并统计载荷循环。

文中采用Miner线性损伤累积理论，对太阳翼基板进行疲劳寿命分析。根据Miner线性损伤假设，每一次应力循环对结构造成的损伤是可以线性叠加的，各应力之间相互独立，不考虑加载次序，当损伤累积到某一临界值，即认为试件发生疲劳破坏。对于 i级载荷循环了 ni次时，造成的疲劳损伤 Di为：

则所有各级载荷累积造成的疲劳损伤可表示为：

疲劳寿命T等于：

式中：Ni表示应力幅值为i级时发生疲劳破坏的循环次数，一般由实验获得；DCR表示疲劳损伤临界值，一般取1。

3.3 声学疲劳分析结果

图7 加载60 s时太阳翼基板声学疲劳Fig.7 Random acoustic fatigue for solar panel under 60 s

噪声激励持续时间为 60 s的结构疲劳损伤和疲劳寿命如图7所示。可以看出，由于模型结构具有对称性，混响场内声压均匀分布，疲劳损伤分布也呈现沿基板长轴的对称性。其中太阳翼基板中心区域疲劳损伤最大，为危险点。危险点在多阶模态下的应力都处于较高水平，对响应贡献较大的二阶、三阶模态中应力集中表现明显，如图8所示。

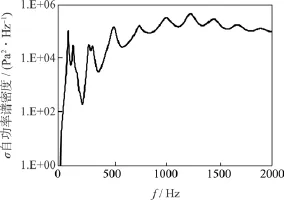
图8 危险点应力自功率谱密度Fig.8 Self power spectral density of stress in dangerous location

综上所述，在噪声激励持续作用 60 s后，损伤率分布呈沿结构长轴对称状态，疲劳危险点处最大损伤率D=0.0232，太阳翼基板未出现疲劳破坏，最短疲劳寿命T=2.58×103s。

4　结论

文中采用三明治夹心板理论对复合材料太阳翼基板进行了力学等效处理，建立了复合材料太阳翼基板的声振耦合FE/BEM分析模型，结合噪声试验结果，采用基于频率响应的模型验证方法，对模型的不确性参数进行了修正。以此为基础，采用Miner线性损伤累积理论及雨流计数法，仿真分析了太阳翼基板的疲劳寿命。研究结果表明：

1）采用三明治夹心板理论对碳纤维蒙皮-蜂窝铝芯太阳翼基板进行等效处理，简化了计算代价，同时能准确反映结构动力学特性。

2）根据噪声试验结果，采用基于频率响应的模型验证方法，对蜂芯等效参数进行了修正，提高了模型的预测精度。

3）太阳翼基板疲劳危险点出现在基板中心区域，该区域在多阶模态中都处于高应力水平，是疲劳破坏的主要区域。

[1] FATERNI A, YANG L. Cumulative Fatigue Damage and Life Prediction Theories: A Survey of the State of the Artfor Homogeneous Materials[J]. International Journal of Fatigue, 1998, 20: 9—34.

[2] PETRUCCI G, ZUCCARELLO B. Fatigue Life Prediction under Wide Band Random Loading[J]. Fatigue Fracture Engineering Material Structural, 2004, 24: 1183—1195.

[3] 姚起杭, 杨学勤. 飞机结构声疲劳设计手册[M]. 北京:航空工业出版社, 1998. YAO Qi-hang, YANG Xue-qin. Aircraft Structural Fatigue Design Handbook[M]. Beijing: Aviation Industry Press, 1998.

[4] SOCIE D F, MORROW J. A Procedure for Estimating the Total life of Notched and Crack Members[J]. Eng, 1979(11): 851—899

[5] 刘景光, 朱广荣. 有限元法在声疲劳分析DSR法中应用技术研究[C]// 第十届全国振动理论及应用学术会议论文集. 南京: 南京航空航天大学, 2011: 1095—1100. LIU Jing-guang, ZHU Guang-rong. Study on the Application of Finite Element Method in DSR Method of Acoustic Fatigue Analysis[C]// Proceedings of the Tenth National Conference on Vibration Theory and Application. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011: 1095—1100.

[6] 姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2004. YAO Wei-xing. Analysis on Structural Fatigue Life[M]. Beijing: National Defense Industry Press, 2004.

[7] 李超. 基于功率谱密度的疲劳寿命估算[J]. 机械设计与研究, 2005, 21(4): 628. LI Chao. Estimation of Fatigue Life Based on Power Spectral Density[J]. Mechanical Design and Research, 2005, 21(4): 628.

[8] 曹明红, 葛森, 齐丕骞. 随机振动疲劳频域分析方法的对比研究[J]. 结构强度研究, 2008(21):94—95. CAO Ming-hong, GE Sen, QI Pi-qian. Comparative Study on Frequency Domain Analysis Method of Random Vibration Fatigue[J]. Structural Strength Study, 2008.

[9] 沙云东, 郭小鹏, 张军. 基于应力概率密度和功率谱密度法的随机声疲劳寿命预估方法研究[J]. 振动与冲击, 2010(1): 162—165. SHA Yun-dong, GUO Xiao-peng, ZHANG Jun. Research on Random Acoustic Fatigue Life Prediction Method Based on Stress Probability Density and Power Spectral Density Method[J]. Journal of Vibration and Shock, 2010(1): 162—165.

[10] BISHOP N W M, FRANK S. Fatigue Life Prediction from Power Spectral Density Data, Part 2: Recent Developments[J]. Environmental Engineering, 1989, 2(2): 11—15.

[11] 盛聪, 曾福明, 濮海玲. 应用OptiStruct软件的太阳翼基板结构优化[J]. 航天器工程, 2011(6): 63—68. SHENG Cong, ZENG Fu-ming, PU Hai-ling. Optimization of Solar Panel Structure by Using OptiStruct[J]. Spacecraft Engineering, 2011(6): 63—68.

[12] 刘捷, 陈志刚, 尚仰宏. 蜂窝夹层结构天线罩疲劳特性研究[C]// 2007年机械电子学学术会议论文集. 北京: 中国电子学会电子机械工程分会, 2007. LIU Jie, CHEN Zhi-gang, SHANG Yang-hong. Fatigue Property Study of the Honeycomb Sandwich Radome[C]// Proceedings of the 2007 Conference on mechanical electronics. Beijing: Electronic Mechanical Engineering Branch of China Electronic Society, 2007.

[13] 胡玉琴. 铝蜂窝夹层板等效模型研究及数值分析[D].南京: 南京航空航天大学, 2008. HU Yu-qin. Equivalent Model and Numerical Analysis of Aluminum Honeycomb Sandwich Plate[D]. Najing: NUAA, 2008.

Acoustic Fatigue on Composite Solar Panel

ZHENG Ling1, ZHANG Wei1, ZENG Jie1, XIANG Shu-hong2, LI Ye2, YANG Jiang2
(1.The State Key Laboratory of Mechanical Transmission, College of Automotive Engineering, Chongqing University, Chongqing 400044, China; 2.Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)

The investigation on the fatigue behavior and its evolution law of spacecrafts under sound excitation is very significant to ensure the safety of the spacecraft in the launch. In this paper, the acoustic fatigue of composite solar panel was analyzed and investigated. Finite Element (FE) and Boundary Element (BE) methods were used to establish numerical analysis models for acoustic response in composite solar panel. The numerical analysis model was verified and validated by acoustic test of the solar panel in reverberation chamber. The results showed that the fatigue damage was distributed symmetrically along the long axis of the structure and the fatigue damage at the point of maximum rate of D=0.0232 when subjected to sound excitation sustained action over 60 s. No fatigue failure appeared and the shortest lifetime of solar panel was 2.58×103s. All results lead to the conclusion that the center location in composite solar panel has the shortest fatigue life due to high stress level caused by several vibro-acoustic coupling modes, and easily gets broken.

acoustic excitation; EF/BEM; reverberation; acoustic response; fatigue life

2016-08-01；Revised：2016-09-02

10.7643/ issn.1672-9242.2016.05.007

TJ086

A

1672-9242(2016)05-0041-07

2016-08-01；

2016-09-02

郑玲（1963—），女，浙江平阳人，博士，教授，主要研究方向为振动噪声控制。

Biography：ZHENG Ling （1963—），Female， from Pingyang， Zhejiang， Ph. D， Professor， Research focus: noise and vibration control.